斯特林数及其相关知识和应用
引言
在组合数学，Stirling数可指两类数，第一类Stirling数和第二类Stirling数，都是由18世纪数学家James Stirling提出的。
Stirling数有两种，第一类Stirling数和第二类Stirling数，它们自18世纪以来一直吸引许多数学家的兴趣，如欧拉、柯西、西尔沃斯特和凯莱等。后来哥本哈根（Copenhagen）大学的尼尔森（Niels Nielsen，1865-1931）提出了"Stirlingschen Zahlen erster Art" (第一类Stirling数)和"Stirlingschen Zahlen zweiter Art" (第二类Stirling数)，首次把这两类数冠以「Stirling数」之名 。因为苏格兰数学家斯特林（J. Stirling, 1692-1770）首次发现这些数并说明了它们的重要性。
——来自于百度百科
此外，由于拉赫数与斯特林数关系密切，有时候也将拉赫数（Lah number）称为第三类斯特林数。
注：第二类斯特林数却在斯特林的相关著作和具体数学中被首先描述，同时也比第一类斯特林数常用得多。
自然幂，上升幂和下降幂
在介绍斯特林数之前，我先介绍一下自然幂，上升幂和下降幂，因为斯特林数的性质和这三种幂紧密相关。
自然幂符号及公式
\[m^n=\prod_{i=0}^{n-1} m
\]
上升幂符号及公式
\[m^{\overline{n}}=\prod_{i=0}^{n-1}(m+i)
\]
下降幂符号及其公式
\[m^{\underline{n}}=\prod_{i=0}^{n-1}(m-i)
\]
上升幂和下降幂的转换
\[(-m)^{\overline{n}}=(-1)^nm^{\underline{n}}
\]
\[(-m)^{\overline{n}}=(-1)^nm^{\underline{n}}
\]
另外
其实自然幂和上升幂，自然幂和下降幂之间是可以相互转换的，在之后的前两类斯特林数的性质中会讲述。
第一类斯特林数
介绍
第一类斯特林数（斯特林轮换数）\(\begin{bmatrix} n\\ m\end{bmatrix}\)，表示将 \(n\) 个两两不同的元素，划分成 \(m\) 个互不区分的非空置换的方案数。
注：一个轮换是一个收尾相接的环形排列。两个可以通过旋转而互相得到的轮换是等价的（我们不认为两个可以通过翻转而相互得到的轮换等价）。
递推式
\[\begin{bmatrix} n\\ m\end{bmatrix}=\begin{bmatrix} n-1\\ m-1\end{bmatrix}+(n-1)\begin{bmatrix} n-1\\ m\end{bmatrix}
\]
边界为：\(\begin{bmatrix} n\\0\end{bmatrix}=[n=0]\) 。
运用组合意义证明：
-
新加入的元素独立作为一个置换，方案数为 \(\begin{bmatrix} n-1\\ m-1\end{bmatrix}\) 。
-
新加入的元素加入现有的置换当中，因为对任意长度为 \(l\) 的置换插入该置换的方案数为 \(l\) ，当前置换总长为 \(n-1\) ，所以方案数为 \((n-1)\begin{bmatrix} n-1\\ m\end{bmatrix}\) 。
根据加法原理，将两式相加即可得到递推式。
性质
-
\[n!=\sum_{i=0}^n\begin{bmatrix}n\\ i\end{bmatrix} \]
理解：对于一个排列 \(P\) 我们可以将所有的 \((p_i, i)\) 连边，一个环则为一组轮换，每种排列一一每种置换。
证明：数学归纳法，请读者自行证明。
-
\[m^{\overline{n}}=\sum_{i=0}^n\begin{bmatrix} n\\i \end{bmatrix}m^i \]
证明：
- 显然，在 \(n=0\) 的时候左右两边相等。
- 设 \(n=k\) 的时候两边相等，即 \(m^{\overline{k}}=\sum\limits_{i=0}^k\begin{bmatrix} k\\ i \end{bmatrix}m^i\)。
- 则在 \(n=k+1\) 时：
\[\begin{aligned}
左边&=m^{\overline{k+1}}\\
&=(m+k)m^{\overline{k}}\\
&=(m+k)\sum_{i=0}^k\begin{bmatrix} k\\ i \end{bmatrix}m^i
\end{aligned}
\]
\[\begin{aligned}
右边&=\sum_{i=0}^{k+1}\begin{bmatrix} k+1\\ i \end{bmatrix}m^i\\
&=\sum_{i=0}^{k+1}(\begin{bmatrix} k\\ i-1 \end{bmatrix}+k\begin{bmatrix} k\\ i \end{bmatrix})m^i\\
&=\sum_{i=0}^{k+1}\begin{bmatrix} k\\ i-1 \end{bmatrix}m^i+k\sum_{i=0}^{k+1}\begin{bmatrix} k\\ i \end{bmatrix}m^i\\
&=\sum_{i=0}^{k}\begin{bmatrix} k\\ i \end{bmatrix}m^{i+1}+k\sum_{i=0}^{k}\begin{bmatrix} k\\ i \end{bmatrix}m^i\\
&=(m+k)\sum_{i=0}^{k}\begin{bmatrix} k\\ i \end{bmatrix}m^i\\&=左边
\end{aligned}
\]
-
即 \(m^{\overline{k+1}}=\sum_{i=0}^{k+1}\begin{bmatrix} k+1\\ i \end{bmatrix}m^i\)
-
改命题由此得证。
-
\[m^{\underline{n}}=\sum_{i=0}^n(-1)^{n-i}\begin{bmatrix} n\\ i \end{bmatrix}m^i \]
证明：
- 由上式可得：
\[\begin{aligned}
m^{\underline{n}}&=(-1)^n\cdot (-1)^{n}m^{\underline{n}}\\
&=(-1)^n(-m)^{\overline{n}}\\
&=\sum_{i=0}^n\begin{bmatrix} n\\ i \end{bmatrix}(-m)^i\\
&=(-1)^n\sum_{i=0}^n\begin{bmatrix} n\\ i \end{bmatrix}(-m)^i\\
&=(-1)^n\sum_{i=0}^n(-1)^{-i}\begin{bmatrix} n\\ i \end{bmatrix}m^i\\
&=\sum_{i=0}^n(-1)^{n-i}\begin{bmatrix} n\\ i \end{bmatrix}m^i
\end{aligned}
\]
通项公式
第一类斯特林数目前没有实用的通项公式。
同一行第一类斯特林数的计算
由于 \(O(n\log^2n)\) 的分治FFT的做法已经烂大街。
所以我们讲讲时间复杂度为 \(O(n\log n)\) 的做法（虽然还是逃不过多项式）。
考虑构造生成函数 \(F(x)^n=\prod\limits_{i=0}^{n-1}(x+i)=\prod\limits_{i=0}^{n}a_ix^i\) ，可以根据 \(m^{\overline{n}}=\sum\limits_{i=0}^n\begin{bmatrix} n\\ i \end{bmatrix}m^i\) 得到其中的 \(a_i=\begin{bmatrix}n\\ i\end{bmatrix}\) 。
显然 \(F(x)^{2n}=F(x)^nF(x+n)^n\) 。
\[\begin{aligned}
F(x+n)^n&=\sum_{i=0}^n a_i(x+n)^i\\
&=\sum_{i=0}^n a_i\sum_{j=0}^n {i\choose j} x^jn^{i-j}\\
&=\sum_{i=0}^n \sum_{j=i}^n {j\choose i} x^in^{j-i}
a_j\\
&=\sum_{i=0}^n \sum_{j=i}^n \frac{j!}{i!(j-i)!} x^in^{j-i}a_j\\
&=\sum_{i=0}^n\frac{1}{i!} (\sum_{j=i}^n a_jj! \frac{n^{j-i}}{(j-i)!}) x^i
\end{aligned}
\]
我们可以通过左半部分系数得到右半部分系数由此得到全部的系数。
时间复杂度: \(T(n)=T(\frac n 2)+O(n\log n)=O(n\log n)\) 。
/**
* unicode: UTF-8
* name: 同一行第一类斯特林数的计算
* author: wangjunrui
* created: 2022.07.03 周日 21:23:22 (Asia/Shanghai)
**/
#include <algorithm>
#include <cstdio>
#define ll long long
#define lll __int128
#define ull unsigned ll
#define lowbit(x) (x & (-x))
template <typename T>
inline void read(T &x)
{
x = 0;
char s = (char)getchar();
bool f = false;
while (!(s >= '0' && s <= '9'))
{
if (s == '-')
f = true;
s = (char)getchar();
}
while (s >= '0' && s <= '9')
{
x = (x << 1) + (x << 3) + s - '0';
s = (char)getchar();
}
if (f)
x = (~x) + 1;
}
template <typename T, typename... T1>
inline void read(T &x, T1 &...x1)
{
read(x);
read(x1...);
}
template <typename T>
inline void ckmin(T &x, T y)
{
if (x > y)
x = y;
}
template <typename T>
inline void ckmax(T &x, T y)
{
if (x < y)
x = y;
}
using namespace std;
constexpr int N = 8e5 + 5;
constexpr int mod = 167772161;
constexpr int inv3 = 55924054;
inline ll quickpow(ll a, int b)
{
ll res = 1;
while (b)
{
if (b & 1)
(res *= a) %= mod;
(a *= a) %= mod;
b >>= 1;
}
return res;
}
ll fac[N], ifac[N];
inline ll C(int n, int m)
{
return fac[n] * fac[m] % mod * fac[n - m] % mod;
}
ll A[N], B[N];
int len, limit, rk[N];
inline void init(int all)
{
len = 0, limit = 1;
while (limit <= all)
{
limit <<= 1;
++len;
}
for (int i = 0; i < limit; ++i)
rk[i] = (rk[i >> 1] >> 1) | ((i & 1) << (len - 1));
}
inline void NTT(ll *dp)
{
for (int i = 0; i < limit; ++i)
if (i < rk[i])
swap(dp[i], dp[rk[i]]);
for (int mid = 1; mid < limit; mid <<= 1)
{
ll gn = quickpow(3, (mod - 1) / (mid << 1));
for (int j = 0; j < limit; j += mid << 1)
{
ll g = 1;
for (int i = 0; i < mid; ++i, (g *= gn) %= mod)
{
ll x = dp[i + j], y = dp[i + j + mid] * g % mod;
dp[i + j] = (x + y) % mod;
dp[i + j + mid] = (x - y) % mod;
}
}
}
}
inline void INTT(ll *dp)
{
for (int i = 0; i < limit; ++i)
if (i < rk[i])
swap(dp[i], dp[rk[i]]);
for (int mid = 1; mid < limit; mid <<= 1)
{
ll gn = quickpow(inv3, (mod - 1) / (mid << 1));
for (int j = 0; j < limit; j += mid << 1)
{
ll g = 1;
for (int i = 0; i < mid; ++i, (g *= gn) %= mod)
{
ll x = dp[i + j], y = dp[i + j + mid] * g % mod;
dp[i + j] = (x + y) % mod;
dp[i + j + mid] = (x - y) % mod;
}
}
}
ll inv = quickpow(limit, mod - 2);
for (int i = 0; i < limit; ++i)
(dp[i] *= inv) %= mod;
}
ll answer[N];
inline void solve(int n)
{
if (n == 1)
{
answer[1] = 1;
return;
}
int las = n / 2;
solve(las);
for (int i = 0; i <= las; ++i)
A[las - i] = answer[i] * fac[i] % mod;
ll power = 1;
for (int i = 0; i <= las; ++i, (power *= las) %= mod)
B[i] = power * ifac[i] % mod;
init(las * 2);
NTT(A), NTT(B);
for (int i = 0; i < limit; ++i)
(A[i] *= B[i]) %= mod;
INTT(A);
reverse(A, A + las + 1);
for (int i = 0; i <= las; ++i)
(A[i] *= ifac[i]) %= mod;
fill(A + las + 1, A + limit, 0);
fill(B + 0, B + limit, 0);
init(n);
NTT(answer), NTT(A);
for (int i = 0; i < limit; ++i)
(answer[i] *= A[i]) %= mod;
INTT(answer);
fill(A + 0, A + limit, 0);
if (n & 1)
for (int i = n; i >= 1; --i)
answer[i] = (answer[i - 1] + (n - 1) * answer[i]) % mod;
}
signed main()
{
int n;
read(n);
fac[0] = 1;
for (int i = 1; i <= n; ++i)
fac[i] = fac[i - 1] * i % mod;
ifac[n] = quickpow(fac[n], mod - 2);
for (int i = n; i >= 1; --i)
ifac[i - 1] = ifac[i] * i % mod;
if(n)
solve(n);
else
answer[0] = 1;
for (int i = 0; i <= n; ++i)
printf("%lld ", (answer[i] + mod) % mod);
putchar('\n');
return 0;
}
同一列第一类斯特林数的计算
在路上了
第二类斯特林数
介绍
第二类斯特林数（斯特林子集数）\(\begin{Bmatrix}n\\ m\end{Bmatrix}\) ，表示将 \(n\) 个两两不同的元素，划分为 \(m\) 个互不区分的非空子集的方案数。
递推式
\[\begin{Bmatrix}n\\ m\end{Bmatrix}=\begin{Bmatrix}n-1\\ m-1\end{Bmatrix}+m\begin{Bmatrix}n-1\\ m\end{Bmatrix}
\]
边界为 \(\begin{Bmatrix}n\\ 0\end{Bmatrix}=[n=0]\)。
运用组合意义证明：
-
将新元素单独放入一个子集，方案数为 \(\begin{Bmatrix} n-1\\ m-1\end{Bmatrix}\) 。
-
新将新元素放入一个现有的非空子集，方案数为 \(m\begin{Bmatrix} n-1\\ m\end{Bmatrix}\) 。
根据加法原理，将两式相加即可得到递推式。
性质
-
\[m^n=\sum_{i=0}^n\begin{Bmatrix}n \\ i\end{Bmatrix}m^{\underline{i}} \]
证明：
- 显然，在 \(n=0\) 的时候左右两边相等。
- 设 \(n=k\) 的时候两边相等，即 \(m^k=\sum\limits_{i=0}^k\begin{Bmatrix}k \\ i\end{Bmatrix}m^{\underline{i}}\)。
- 则在 \(n=k+1\) 时：
\[\begin{aligned}
左边&=m^{k+1}\\
&=m\cdot m^k\\
&=m\sum\limits_{i=0}^k\begin{Bmatrix}k \\ i\end{Bmatrix}m^{\underline{i}}
\end{aligned}
\]
\[\begin{aligned}
右边&=\sum_{i=0}^{k+1} \begin{Bmatrix}k+1\\ i \end{Bmatrix}m^{\underline i}\\
&=\sum_{i=0}^{k+1} (\begin{Bmatrix}k\\ i-1 \end{Bmatrix}+i\begin{Bmatrix}k\\ i \end{Bmatrix})m^{\underline i}\\
&=\sum_{i=0}^{k+1} \begin{Bmatrix}k\\ i-1 \end{Bmatrix}m^{\underline i}+\sum_{i=0}^{k+1}i\begin{Bmatrix}k\\ i \end{Bmatrix}m^{\underline i}\\
&=\sum_{i=0}^{k} \begin{Bmatrix}k\\ i \end{Bmatrix}m^{\underline {i+1}}+\sum_{i=0}^{k}i\begin{Bmatrix}k\\ i \end{Bmatrix}m^{\underline i}\\
&=\sum_{i=0}^{k} (m-i)\begin{Bmatrix}k\\ i \end{Bmatrix}m^{\underline i}+\sum_{i=0}^{k}i\begin{Bmatrix}k\\ i \end{Bmatrix}m^{\underline i}\\
&=m\sum\limits_{i=0}^k\begin{Bmatrix}k \\ i\end{Bmatrix}m^{\underline{i}}\\
&=左边
\end{aligned}
\]
-
即 \(m^{\overline{k+1}}=\sum_{i=0}^{k+1}\begin{bmatrix} k+1\\ i \end{bmatrix}m^i\)
-
改命题由此得证。
-
\[m^n=\sum_{i=0}^n(-1)^{n-i}\begin{Bmatrix}n \\ i\end{Bmatrix}m^{\overline{i}} \]
证明：
- 由上式可得：
\[\begin{aligned}
m^n&=(-1)^n(-m)^n\\
&=(-1)^n\sum_{i=0}^n\begin{Bmatrix}n \\ i\end{Bmatrix}(-m)^{\underline{i}}\\
&=(-1)^n\sum_{i=0}^n\begin{Bmatrix}n \\ i\end{Bmatrix}(-1)^im^{\overline{i}}\\
&=\sum_{i=0}^n(-1)^{n-i}\begin{Bmatrix}n \\ i\end{Bmatrix}m^{\overline{i}}
\end{aligned}
\]
通项公式
\[\begin{Bmatrix}n\\ m\end{Bmatrix}=\sum_{i=0}^m\frac{(-1)^{m-i}i^n}{i!(m-i)!}
\]
证明：
我们用二项式反演。
令 \(f_i\) 为表示将 \(n\) 个两两不同的元素，划分为 \(i\) 个互不相同的 非空子集 的方案数。
显然 \(f_i=i!\begin{Bmatrix}n\\ i\end{Bmatrix}\) 。
考虑令 \(g_i\) 为表示将 \(n\) 个两两不同的元素，划分为 \(i\) 个互不相同的子集 （可非空） 的方案数。
显然 \(g_i=n^i\) 。
我们考虑 \(f_i\) 其实就是 \(g_i\) 去掉所有的空子集，则我们只要钦定 \(g_i\) 中那些是非空子集就可以写出 \(f_i\) 和 \(g_i\) 的关系了:
\[g_i=\sum_{j=0}^i {i\choose j}f_j
\]
根据二项式反演：
\[\begin{aligned}
f_i&=\sum_{j=0}^i(-1)^{i-j}{i\choose j}g_j\\
&=\sum_{j=0}^i(-1)^{i-j}{i\choose j}j^n\\
&=\sum_{j=0}^i \frac{i!(i-1)^{i-j}j^n}{j!(i-j)!}
\end{aligned}
\]
\[\begin{Bmatrix}n\\ m\end{Bmatrix}=\frac{f_m}{m!}=\sum_{i=0}^m\frac{(-1)^{m-i}i^n}{i!(m-i)!}
\]
同一行第二类斯特林数的计算
根据通项公式，可以发现这是卷积的形式，直接卷积计算即可。
/**
* unicode: UTF-8
* name: 同一行第二类斯特林数的计算
* author: wangjunrui
* created: 2022.07.04 周一 23:35:00 (Asia/Shanghai)
**/
#include <algorithm>
#include <cstdio>
#include <cstring>
#define ll long long
#define lll __int128
#define ull unsigned ll
#define lowbit(x) (x & (-x))
template <typename T>
inline void read(T &x)
{
x = 0;
char s = (char)getchar();
bool f = false;
while (!(s >= '0' && s <= '9'))
{
if (s == '-')
f = true;
s = (char)getchar();
}
while (s >= '0' && s <= '9')
{
x = (x << 1) + (x << 3) + s - '0';
s = (char)getchar();
}
if (f)
x = (~x) + 1;
}
template <typename T, typename... T1>
inline void read(T &x, T1 &...x1)
{
read(x);
read(x1...);
}
template <typename T>
inline void ckmin(T &x, T y)
{
if (x > y)
x = y;
}
template <typename T>
inline void ckmax(T &x, T y)
{
if (x < y)
x = y;
}
using namespace std;
constexpr int N = 8e5 + 5;
constexpr int mod = 167772161;
constexpr int inv3 = 55924054;
inline ll quickpow(ll a, int b)
{
ll res = 1;
while (b)
{
if (b & 1)
(res *= a) %= mod;
(a *= a) %= mod;
b >>= 1;
}
return res;
}
int n;
ll fac[N], ifac[N];
int limit, len, rk[N];
ll A[N], B[N];
inline void init(int all)
{
len = 0, limit = 1;
while (limit <= all)
{
limit <<= 1;
++len;
}
for (int i = 0; i < limit; ++i)
rk[i] = (rk[i >> 1] >> 1) | ((i & 1) << (len - 1));
}
inline void NTT(ll *dp)
{
for (int i = 0; i < limit; ++i)
if (i < rk[i])
swap(dp[i], dp[rk[i]]);
for (int mid = 1; mid < limit; mid <<= 1)
{
ll gn = quickpow(3, (mod - 1) / (mid << 1));
for (int j = 0; j < limit; j += mid << 1)
{
ll g = 1;
for (int i = 0; i < mid; ++i, (g *= gn) %= mod)
{
ll x = dp[i + j], y = dp[i + j + mid] * g % mod;
dp[i + j] = (x + y) % mod;
dp[i + j + mid] = (x - y) % mod;
}
}
}
}
inline void INTT(ll *dp)
{
for (int i = 0; i < limit; ++i)
if (i < rk[i])
swap(dp[i], dp[rk[i]]);
for (int mid = 1; mid < limit; mid <<= 1)
{
ll gn = quickpow(inv3, (mod - 1) / (mid << 1));
for (int j = 0; j < limit; j += mid << 1)
{
ll g = 1;
for (int i = 0; i < mid; ++i, (g *= gn) %= mod)
{
ll x = dp[i + j], y = dp[i + j + mid] * g % mod;
dp[i + j] = (x + y) % mod;
dp[i + j + mid] = (x - y) % mod;
}
}
}
ll inv = quickpow(limit, mod - 2);
for (int i = 0; i < limit; ++i)
(dp[i] *= inv) %= mod;
}
signed main()
{
read(n);
fac[0] = 1;
for (int i = 1; i <= n; ++i)
fac[i] = fac[i - 1] * i % mod;
ifac[n] = quickpow(fac[n], mod - 2);
for (int i = n; i >= 1; --i)
ifac[i - 1] = ifac[i] * i % mod;
for (int i = 0; i <= n; ++i)
{
A[i] = quickpow(i, n) * ifac[i] % mod;
B[i] = (i & 1 ? -1 : 1) * ifac[i];
}
init(n * 2);
NTT(A), NTT(B);
for (int i = 0; i < limit; ++i)
(A[i] *= B[i]) %= mod;
INTT(A);
for (int i = 0; i <= n; ++i)
printf("%lld ", (A[i] + mod) % mod);
putchar('\n');
return 0;
}
同一列第二类斯特林数的计算
在路上了
第三类斯特林数
介绍
第三类斯特林数（拉赫数）$L(n, m)，通常指无符号拉赫数 \(L(n, m)\) ，表示将含有 \(n\) 个元素的集合拆分为 \(m\) 个非空线性有序子集的方法数目。
注： \(\{(1, 2, 3)\}\ne \{(2, 3, 1)\}\) ，\(\{(1, 2), (3)\}\ne \{(3), (1, 2)\}\) 。
拉赫数可以通过上升幂与下降幂之间的转化来定义：
无符号拉赫数
\[m^{\overline{n}}=\sum\limits_{i=0}^nL(n, i)m^{\underline{i}}
\]
\[m^{\underline{n}}=\sum\limits_{i=0}^n(-1)^{n-i}L(n, i)m^{\overline{i}}
\]
有符号拉赫数
\[m^{\overline{n}}=(-1)^n\sum\limits_{i=0}^nL'(n, i)m^{\underline{i}}
\]
\[m^{\underline{n}}=\sum\limits_{i=0}^n(-1)^{i}L'(n, i)m^{\overline{i}}
\]
通项公式
无符号拉赫数
\[L(n, m)={n-1\choose m-1}\frac{n!}{m!}
\]
有符号拉赫数
\[L'(n, m)=(-1)^nL(n, m)=(-1)^n{n-1\choose m-1}\frac{n!}{m!}
\]
递推式
由通项公式可得
\[\begin{aligned}L(n, m)&=\frac{n-m+1}{m(m-1)}L(n, m-1)\\&=(n+m-1)L(n-1, m)+L(n-1, m-1)\end{aligned}
\]
边界：
\(L(n, 0)=0\)，\(L(1, 1)=1\)
性质
下面都是拉赫数的通项公式得出来的
\[\begin{aligned}L(n, m)&={n-1\choose m-1} \frac{n!}{m!}\\&={n\choose m}\frac{(n-1)!}{(m-1)!}\\&={n\choose m}{n-1 \choose m-1}(n-m)!\end{aligned}
\]
\[\begin{aligned}L(n, m)&={n-1\choose m-1} \frac{n!}{m!}\\&=\frac{n!(n-1)!}{m!(m-1)!(n-m)!}\\&=\left(\frac{n!}{m!}\right)^2\frac{m}{n(n-m)!}\end{aligned}
\]
三类斯特林数总结
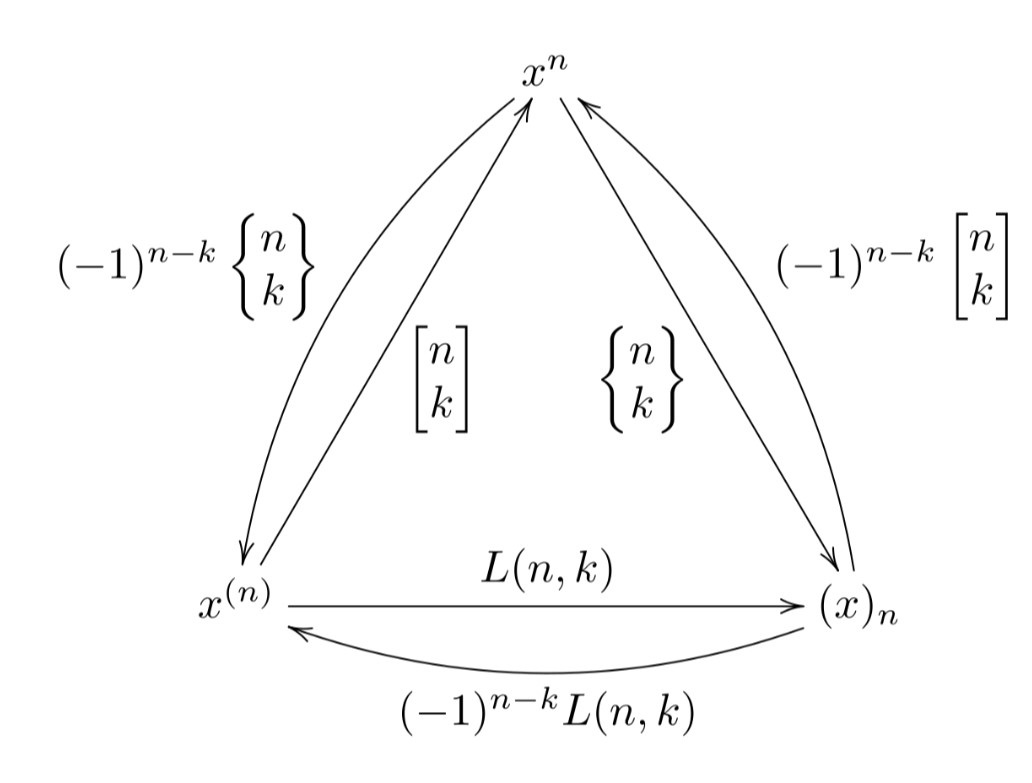
斯特林反演
原来第一类斯特林数和第二类斯特林数之间还能进行反演
前置知识
-
\[m^{\overline{n}}=\sum_{i=0}^n\begin{bmatrix} n\\i \end{bmatrix}m^i \]
-
\[m^{\underline{n}}=\sum_{i=0}^n(-1)^{n-i}\begin{bmatrix} n\\ i \end{bmatrix}m^i \]
-
\[m^n=\sum_{i=0}^n\begin{Bmatrix}n \\ i\end{Bmatrix}m^{\underline{i}} \]
-
\[m^n=\sum_{i=0}^n(-1)^{n-i}\begin{Bmatrix}n \\ i\end{Bmatrix}m^{\overline{i}} \]
具体证明见上面性质部分。
原理
\[\begin{aligned}
m^n&=\sum_{i=0}^n(-1)^{n-i}\begin{Bmatrix}n \\ i\end{Bmatrix}m^{\overline{i}}\\
&=\sum_{i=0}^n(-1)^{n-i}\begin{Bmatrix}n \\ i\end{Bmatrix}\sum_{j=0}^i\begin{bmatrix} i\\ j \end{bmatrix}m^j\\
&=\sum_{i=0}^n m^i\sum_{j=i}^n(-1)^{n-j}\begin{Bmatrix}n \\ j\end{Bmatrix}\begin{bmatrix} j\\ i \end{bmatrix}
\end{aligned}
\]
- 由于这是一个恒等式，我们比对系数可得：
\[\sum_{i=m}^n(-1)^{n-i}\begin{Bmatrix}n \\ i\end{Bmatrix}\begin{bmatrix} i\\ m \end{bmatrix}=[n=m]
\]
- 和上面的推式子一样：
\[\begin{aligned}
m^{\underline{n}}&=\sum_{i=0}^n(-1)^{n-i}\begin{bmatrix} n\\ i \end{bmatrix}m^i\\
&=\sum_{i=0}^n(-1)^{n-i}\begin{bmatrix}n \\ i\end{bmatrix}\sum_{j=0}^i\begin{Bmatrix} i\\ j \end{Bmatrix}m^{\underline j}\\
&=\sum_{i=0}^n m^{\underline i}\sum_{j=i}^n(-1)^{n-j}\begin{bmatrix}n \\ j\end{bmatrix}\begin{Bmatrix} j\\ i \end{Bmatrix}
\end{aligned}
\]
- 由于这是一个恒等式，我们比对系数可得：
\[\sum_{i=m}^n(-1)^{n-i}\begin{bmatrix}n \\ i\end{bmatrix}\begin{Bmatrix} i\\ m \end{Bmatrix}=[n=m]
\]
由此我们就有两个非常对称的恒等式：
\[\sum_{i=m}^n(-1)^{n-i}\begin{Bmatrix}n \\ i\end{Bmatrix}\begin{bmatrix} i\\ m \end{bmatrix}=[n=m]
\]
\[\sum_{i=m}^n(-1)^{n-i}\begin{bmatrix}n \\ i\end{bmatrix}\begin{Bmatrix} i\\ m \end{Bmatrix}=[n=m]
\]
第一种形式
\[f_n=\sum_{i=0}^n \begin{Bmatrix}n \\ i\end{Bmatrix}g_i\Leftrightarrow g_n=\sum_{i=0}^n (-1)^{n-i}\begin{bmatrix}n \\ i\end{bmatrix}f_i
\]
证明：
\[\begin{aligned}
g_n&=\sum_{i=0}^n g_i[n=i]\\
&=\sum_{i=0}^n g_i\sum_{j=i}^n(-1)^{n-j}\begin{bmatrix}n \\ j\end{bmatrix}\begin{Bmatrix} j\\ i \end{Bmatrix}\\
&=\sum_{i=0}^n (-1)^{n-i}\begin{bmatrix}n \\ i\end{bmatrix}\sum_{j=0}^i\begin{Bmatrix} i\\ j \end{Bmatrix}g_j\\
&=\sum_{i=0}^n (-1)^{n-i}\begin{bmatrix}n \\ i\end{bmatrix}f_i
\end{aligned}
\]
第二种形式
证明同上：
\[f_n=\sum_{i=0}^n \begin{bmatrix}n \\ i\end{bmatrix}g_i\Leftrightarrow g_n=\sum_{i=0}^n (-1)^{n-i}\begin{Bmatrix}n \\ i\end{Bmatrix}f_i
\]
证明：
\[\begin{aligned}
g_n&=\sum_{i=0}^n g_i[n=i]\\
&=\sum_{i=0}^n g_i\sum_{j=i}^n(-1)^{n-j}\begin{Bmatrix}n \\ j\end{Bmatrix}\begin{bmatrix} j\\ i \end{bmatrix}\\
&=\sum_{i=0}^n (-1)^{n-i}\begin{Bmatrix}n \\ i\end{Bmatrix}\sum_{j=0}^i\begin{bmatrix} i\\ j \end{bmatrix}g_j\\
&=\sum_{i=0}^n (-1)^{n-i}\begin{Bmatrix}n \\ i\end{Bmatrix}f_i
\end{aligned}
\]
应用
在路上了
