单切线和公切线问题
前言
涉及切线的问题,主要关联的是导数知识和方程思想;
难点总结
-
涉及直线和曲线相切时,难点一是列方程组,来源角度是斜率相等\(k=f'(x_0)\),点在直线上,和点在曲线上三个角度;难点二是解方程组,求解变形方向是求解切点坐标,再求解斜率;
-
涉及直线和曲线[圆、椭圆、双曲线、抛物线]相切时,既可以考虑思路一:联立直线和曲线得到方程组,令\(\Delta=0\)求解;也可以思路二:利用导数知识设切点求切点来求解;思路二可以看成思路一的补充和延申。
单切线
说明:此类型涉及一直线和一曲线
- 类型1:求切点坐标,斜率,切线方程
分析:利用点斜式来求解,其中斜率\(k=f'(x)_{|x=1}=(2x-\cfrac{1}{x^2})_{|x=1}=1\),
切点是\((1,2)\),故切线方程为\(y-2=1(x-1)\),整理为\(y=x+1\)。
分析:\(f'(x)=3x^2+2ax\),则由题意可知,\(\left\{\begin{array}{l}{3x_0^2+2ax_0=-1①}\\{x_0+y_0=0②}\\{y_0=x_0^3+ax_0^2③}\end{array}\right.\),
将②代入③,由于\(x_0\neq 0\),得到\(-1=x_0^2+ax_0\),即\(ax_0=-1-x_0^2\),
代入①得到,\(x_0^2=1\),解得\(x_0=1\)或\(x_0=-1\),代入②得到,切点\(P(1,-1)\)或\(P(-1,1)\),故选\(D\)。
- 类型2:过点处的切线
思路:设经过点\(P(2,4)\)的切线方程与曲线相切于点\(P_0(x_0,y_0)\),则有
\(\begin{cases}y_0=\cfrac{1}{3}x_0^3+\cfrac{4}{3}\\ k=f'(x_0)=x_0^2\\ y-y_0=f'(x_0)(x-x_0) \end{cases}\)
又因为点\(P(2,4)\)在切线方程上,则有\(4-(\cfrac{1}{3}x_0^3+\cfrac{4}{3})=x_0^2(2-x_0)\)
整理得到,\(x_0^3-3x_0^2+4=0\)警示,此处有多个难点:试商法,多项式除法,分组分解法;
【试商法】:令\(x_0=0\),如果上述方程成立,说明方程能分解出因子\(x_0\),本题目中显然不成立;再令\(x_0=1\),上述方程不成立,说明方程不能分解出因子\(x_0-1\);再令\(x_0=-1\),上述方程成立,说明方程能分解出因子\(x_0+1\);这样\(x_0^3-3x_0^2+4\)\(=(x_0+1)\)\((x_0^2+bx_0+c)\)(\(b\),\(c\)是常数,待定),这样做的目的是为了降次;
【分组分解法】:由试商法可以指导我们的分组分解的方向,
如\(x_0^3-3x_0^2+4=(x_0^3+1)-3(x_0^2-1)\)
\(=(x_0+1)(x_0^2-x_0+1)-3(x_0+1)(x_0-1)\)
\(=(x_0+1)(x_0^2-x_0+1-3x_0+3)\)
\(=(x_0+1)(x_0-2)^2=0\);
【多项式除法】:如图所示,
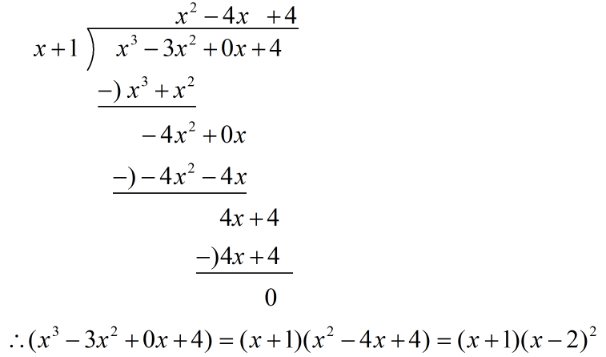
即\((x_0+1)(x_0-2)^2=0\),解得\(x_0=-1\),或\(x_0=2\)
当\(x_0=-1\)时,切点为\((-1,1)\),\(k_1=1\),切线方程为\(x-y+2=0\);
当\(x_0=2\)时,切点为\((2,4)\),\(k_2=4\),切线方程为\(4x-y-4=0\);
总结:设切点,求切点;
思路:平行线法,设和直线\(y=x\)平行且和函数\(y=lnx\)相切的直线为\(y=x+m\),
切点为\(P_0(x_0,y_0)\),则有\(\begin{cases} y_0=x_{0}+ m \\ y_0=lnx_0 \\ f'(x_0)=\cfrac{1}{x_0}=1\end{cases}\);
从而解得\(x_0=1,y_0=0,m=-1\)所以所求的点点距的最小值,就转化为切点\(P_0(1,0)\)到直线\(y=x\)的点线距,
或者两条直线\(y=x,y=x-1\)的线线距了。
分析:设函数\(y=kx\)与函数\(y=lnx\)切点为\(Q(x_0,y_0)\),则有
\(\begin{cases} y_0=kx_0 \\ y_0=lnx_0 \\ k=f'(x_0)=\cfrac{1}{x_0}\end{cases}\);
从而解得\(x_0=e,y_0=1,k=\cfrac{1}{e}\),故切点\(Q\)的坐标为\((e,1)\)
分析:设函数\(y=mx\)与函数\(y=e^x\)切点为\(P(x_0,y_0)\),则有
\(\begin{cases} y_0=mx_0 \\ y_0=e^{x_0} \\ m=f'(x_0)=e^{x_0}\end{cases}\);
从而解得\(x_0=1,y_0=e,m=e\),故切点\(P\)的坐标为\((1,e)\)。
分析:当在曲线上试图寻找一点,让它到直线的距离最小,思考不便于展开时,不妨换位思考,让直线平行移动到和曲线相切得到一个切点,那么所求距离就是切点到直线的点线距,或者是两条平行线之间的线线距。
解析:将函数化简整理为\(y=f(x)=x^2-lnx(x>0)\),再设与已知直线平行的且与曲线相切的直线为\(4x+4y+c=0\),
切点为\((x_0,y_0)\),则由\(f'(x)=2x-\cfrac{1}{x}\),
得到\(\begin{cases}k=f'(x_0)=2x_0-\cfrac{1}{x_0}=-1①\\4x_0+4y_0+c=0②\\y_0=x_0^2-lnx_0③\end{cases}\),
解①得到\(x_0=-1(舍去)\)或\(x_0=\cfrac{1}{2}\),代入③得到\(y_0=\cfrac{1}{4}+ln2\),
故切点\((\cfrac{1}{2},\cfrac{1}{4}+ln2)\)到已知直线\(4x+4y+1=0\)的距离就是所要求解的距离。
故所求距离\(d=\cfrac{|4\times \cfrac{1}{2}+4\times(\cfrac{1}{4}+ln2)+1|}{\sqrt{4^2+4^2}}=\cfrac{\sqrt{2}}{2}(1+ln2)\)
法1: 从数的角度入手,比较好计算但是不太好想;
设切点是 \(P(x_{0}, x_{0}-a\ln x_{0})\), 由\(f'(x)=1-\cfrac{a}{x}\),
则以 \(P\) 为切点的切线方程为 \(y-x_{0}+a\ln x_{0}=(1-\cfrac{a}{x_{0}})(x-x_{0})\),
因为该切线过原点,所以 \(0-x_{0}+a\ln x_{0}=(1-\cfrac{a}{x_{0}})(0-x_{0})\), \(\ln x_{0}=1\), \(x_{0}=e\),
所以 \(k=1-\cfrac{a}{e}>0\), 所以 \(a<e\) 且 \(a\neq 0\),故选 \(A\) .
法2: 从形的角度入手,比较好想,但是计算有难度;
由题可知,直线 \(y=kx(k>0)\) 和曲线 \(f(x)=x-a\ln x(a\neq0)\) 相切,
转化为方程\(kx=x-a\ln x\)仅有一解,即方程\((1-k)x=a\ln x\)仅有一解,
即直线 \(y=(1-k)x\) 与曲线 \(y=a\ln x\) 相切;以下分类讨论:
当\(a>0\)时,设切点为\(P(x_0,y_0)\),则其必满足条件\(\left\{\begin{array}{l}{y_0=a\ln x_0}\\{y_0=(1-k)x_0}\\{1-k=\cfrac{a}{x_0}}\end{array}\right.\),
解得,\(x_0=e\),此时由图可知,直线\(y=(1-k)x\)的斜率必须满足\(0<1-k<1\)解释:由于\(k>0\),故\(1-k<1\)\(\quad\),
故\(0<\cfrac{a}{e}<1\),故\(0<a<e\),
当\(a<0\)时,设切点为\(P(x_0,y_0)\),则其必满足条件\(\left\{\begin{array}{l}{y_0=a\ln x_0}\\{y_0=(1-k)x_0}\\{1-k=\cfrac{a}{x_0}}\end{array}\right.\),
解得,\(x_0=e\),此时由图可知,直线\(y=(1-k)x\)的斜率必须满足\(1-k<0\),
故\(\cfrac{a}{e}<0\),故\(a<0\),
综上所述,\(a\in (-\infty,0)\cup(0,e)\), 故选 \(A\) .
公切线
说明:此类型涉及一直线和两曲线
- 求公切线的斜率,截距,求公切线方程
思路:设直线\(y=kx+b\)与函数\(C_0:y=lnx+2\)相切于点\(P_0(x_0,y_0)\),
直线\(y=kx+b\)与函数\(C_1:y=ln(x+1)\)相切于点\(P_1(x_1,y_1)\),
则由题可知,在点\(P_0(x_0,y_0)\)处的切线方程为\(y-y_0=f'(x_0)(x-x_0)\),
即\(y-(lnx_0+2)=\cfrac{1}{x_0}(x-x_0)\),化简为\(y=\cfrac{1}{x_0}x+lnx_0+1\);
在点\(P_0(x_0,y_0)\)处的切线方程为\(y-y_1=f'(x_1)(x-x_1)\),
即\(y-ln(x_1+1)=\cfrac{1}{x_1+1}(x-x_1)\),化简为\(y=\cfrac{1}{x_1+1}x+ln(x_1+1)-\cfrac{x_1}{x_1+1}\)
由这两条切线是同一条【同一法】可知,
\(\begin{cases} k=\cfrac{1}{x_0}=\cfrac{1}{x_1+1} \\ b=lnx_0+1=ln(x_1+1)-\cfrac{x_1}{x_1+1} \end{cases}\), 即\(\begin{cases}x_0=x_1+1\\1=-\cfrac{x_1}{x_1+1}\end{cases}\),
解得:\(\begin{cases} x_0=x_1+1 \\ x_0=\cfrac{1}{2},x_1=-\cfrac{1}{2}\end{cases}\)
所以\(b=1+lnx_0=1+ln(\cfrac{1}{2})=1-ln2\).
反思:还可以求解\(k\)值,切线方程等。
对应练习:【2024 新课标全国Ⅰ卷第13题】若曲线 \(y=e^x+x\) 在点 \((0,1)\) 处的切线也是曲线 \(y=\ln(x+1)+a\) 的切线,则 \(a=\)__________ .
提示:用上述的同一法可以求解 \(a=\ln 2\) .
- 求解公切线的条数
法1:做出两个曲线的图像,由图像的位置观察可得,选\(C\);
法2:计算法,设函数\(g(x)=x^2+2x+3\)上的切点为\(P(x_0,y_0)\),
则\(k=g'(x_0)=2x_0+2\)①,又\(y-y_0=(2x_0+2)(x-x_0)\)②,
且有\(y_0=x_0^2+2x_0+3\)③,将③代入②,
得到切线方程为\(2(x_0+1)x-y+3-x_0^2=0\),再联立\(f(x)=y=-x^2\),
消去\(y\),得到\(x^2+2(x_0+1)x+3-x_0^2=0\),
由切线和函数\(y=f(x)\)也相切,则\(\Delta=0\),
得到\(x_0^2+x_0-1=0\),解得\(x_0=\cfrac{\pm\sqrt{5}-1}{2}\),
故情形一,切点为\((\cfrac{\sqrt{5}-1}{2},\cfrac{\sqrt{5}+7}{2})\),斜率为\(k=\sqrt{5}+1\);
情形二,切点为\((\cfrac{-\sqrt{5}-1}{2},\cfrac{-\sqrt{5}+7}{2})\),斜率为\(k=-\sqrt{5}+1\);
故满足题意的切点个数有2个,故选\(C\)。
对计算结果的图形验证如下所示:
- 由公切线的存在性问题求参数的取值范围
分析:本题目属于公切线问题,可以先求得过点处的与\(y=x^3\)相切的直线,然后联立直线和抛物线(二次函数),利用\(\Delta=0\)来解决。
设过点\((1,0)\)的直线与曲线\(y=x^3\)相切于点\((x_0,y_0)\),由\(f'(x)=3x^2\)可得,
\(\begin{cases}k=f'(x_0)=3x_0^2\\y_0=x_0^3\\y-y_0=f'(x_0)(x-x_0)\end{cases}\),
又点\((1,0)\)在切线上,故有\(0-x_0^3=3x_0^2(1-x_0)\),解得\(x_0=0\)或\(x_0=\cfrac{3}{2}\);
当\(x_0=0\)时,\(y_0=0\),即切点是\((0,0)\),斜率\(k=0\),故切线方程为\(y=0\),
与曲线\(y=ax^2+\cfrac{15}{4}x-9\)相切,消\(y\)得到\(ax^2+\cfrac{15}{4}x-9=0\),
利用\(\Delta=(\cfrac{15}{4})^2+4\times 9a=0\),解得\(a=-\cfrac{25}{64}\);
当\(x_0=\cfrac{3}{2}\)时,\(y_0=\cfrac{27}{8}\),即切点是\((\cfrac{3}{2},\cfrac{27}{8})\),斜率\(k=\cfrac{27}{4}\),
故切线方程为\(y-\cfrac{27}{8}=\cfrac{27}{4}(x-\cfrac{3}{2})\),
与曲线\(y=ax^2+\cfrac{15}{4}x-9\)相切,消\(y\)得到\(ax^2-3x-\cfrac{9}{4}=0\),
利用\(\Delta=(-3)^2-4\times a\times(-\cfrac{9}{4})=0\),解得\(a=-1\);
综上,\(a=-1\)或\(-\cfrac{25}{64}\),故选A。
反思总结:直线与三次曲线的相切问题,我们用导数解决;直线与二次曲线(如圆、椭圆、双曲线、抛物线等)的相切问题,我们常用\(\Delta=0\)来解决。
分析:由\(y=ax^2\),得到\(y'=2ax\);由\(y=e^x\)得到\(y'=e^x\);
曲线\(C_1:y=ax^2(a>0)\)与曲线\(C_2:y=e^{-x}\)有公共切线,
设公切线与\(C_1:y=ax^2(a>0)\)相切于点\((x_1,ax_1^2)\),
公切线与\(C_1:y=e^x(a>0)\)相切于点\((x_2,e^{x_2})\),
则由切线斜率相等,可得\(2ax_1=e^{x_2}=\cfrac{e^{x_2}-ax_1^2}{x_2-x_1}\),
可得\(2x_2=x_1+2\);便于变量集中,
故由\(2ax_1=e^{x_2}\),分离参数得到\(a=\cfrac{e^{x_2}}{2x_1}=\cfrac{e^{\frac{x_1}{2}+1}}{2x_1}\)
令\(f(x)=\cfrac{e^{\frac{x}{2}+1}}{2x}\),即上式为\(a=f(x)(由图可看出x>0)\)由实数解,
转化为求函数\(f(x)\)的值域问题。
\(f'(x)=\cfrac{e^{\frac{x}{2}+1}\cdot \cfrac{1}{2}\cdot 2x-e^{\frac{x}{2}+1}\cdot 2}{(2x)^2}\),
\(=\cfrac{e^{\frac{x}{2}+1}\cdot(x-2)}{4x^2}\),
故\(x\in(0,2)\)上,\(f'(x)<0\),\(f(x)\)单调递减,
\(x\in(2,+\infty)\)上,\(f'(x)>0\),\(f(x)\)单调递增,
故\(f(x)_{极小}=f(x)_{min}=f(2)=\cfrac{e^2}{4}\);
故\(a\)的取值范围为\([\cfrac{e^2}{4},+\infty)\)。
分析:由于曲线\(C\)存在与直线\(y=ex\)垂直的切线,设曲线的切线的切点坐标\((x_0,y_0)\),
则有\(f'(x_0)=e^{x_0}-m=-\cfrac{1}{e}\),即方程\(m=e^{x_0}+\cfrac{1}{e}\)有解,
故转化为求函数\(g(x_0)=e^{x_0}+\cfrac{1}{e}\)的值域,
由于\(x_0\in R\),故\(g(x_0)\in (\cfrac{1}{e},+\infty)\),
故实数\(m\)的取值范围是\(m\in (\cfrac{1}{e},+\infty)\)。
- 由公切线的存在性问题求切点坐标的取值范围
分析:由切线\(l\)与函数\(y=x^2\)相切与点\((x_0,x_0^2)\),则得到切线的点斜式方程为:\(y-x_0^2=2x_0(x-x_0)\)
由切线\(l\)与函数\(y=lnx\)相切与点\((x_1,lnx_1)\),则得到切线的点斜式方程为:\(y-lnx_1=\cfrac{1}{x_1}(x-x_1)\)且\(x_1\in(0,1)\)
又两条切线是同一条直线,得到
\(\begin{cases} 2x_0=\cfrac{1}{x_1} \hspace{0.5cm} x_1\in(0,1) \hspace{1cm}①\\\ x_0^2=1-lnx_1 \hspace{3cm}②\end{cases}\)
法1:不等式性质法
由于\(x_1\in(0,1)\),由①得到\(x_0>\cfrac{1}{2}\);由于\(1-lnx_1>1\),由②得到\(x_0>1\),综合得到\(x_0>1\),故选\(D\).
法2:零点存在性定理
由方程组消掉\(x_1\)得到新方程\(x_0^2-ln2x_0-1=0\),令函数\(f(x_0)=x_0^2-ln2x_0-1\),由零点存在性定理可得,\(D\) 是正确的。当然我们还可以结合二分法,得到更小的解的区间。
- 由公切线的存在性问题求参数的最值
分析:本题目属于公切线问题,设切点为\(P(x_0,y_0)\),则满足以下方程组
\(\begin{cases}f'(x_0)=g'(x_0)①\\y_0=f(x_0)=\cfrac{3}{2}x_0^2-2ax_0②\\y_0=g(x_0)=a^2lnx_0+b③\end{cases}\)
由①得到\(x_0=a\)或\(x_0=-\cfrac{a}{3}(a>0,不符合舍去)\)
由②③得到,\(\cfrac{3}{2}x_0^2-2ax_0=a^2lnx_0+b\),将\(x_0=a\)代入,
分离参数\(b\)得到,\(b=-\cfrac{1}{2}a^2-a^2lna\)。
设\(h(a)=-\cfrac{1}{2}a^2-a^2lna(a>0)\),则\(b_{max}=h(a)_{max}\);
接下来,用导数研究\(h(a)\)的单调性。
\(h'(a)=-2a(1+lna)\),借助\(y=1+lna\)的大致图像可知,
\(h(a)\)在区间\((0,\cfrac{1}{e})\)单调递增,在区间\((\cfrac{1}{e},+\infty)\)上单调递减,
则\(h(a)_{max}=h(\cfrac{1}{e})=\cfrac{1}{2e^2}\)
即\(b_{max}=\cfrac{1}{2e^2}\),选A。
- 直线与曲线无交点
法1:导数法,仿上题可知,函数\(y=mx\)与函数\(y=e^x\)的图像没有交点,所求的\(m\)取值范围为$0\leq m<e $。
法2:转化法,则方程\(e^x=mx\)无解,即方程\(m=\cfrac{e^x}{x}\)无解,令函数\(g(x)=\cfrac{e^x}{x}\),
利用导数求得值域为\(g(x)\in (-\infty,0)\cup[e,+\infty)\),故要使得方程\(m=g(x)\)无解,得到$0\leq m<e $。
- 讨论公切线的条数
(1)确定方程\(f(x)=\cfrac{x+1}{x-1}\)实数根的个数。
(2)我们把与两条曲线都相切的直线叫作这两条曲线的公切线,试确定曲线\(y=f(x),y=g(x)\)公切线的条数,并证明你的结论。
分析:(1)由\(f(x)=\cfrac{x+1}{x-1}\)得到,\(lnx=\cfrac{x+1}{x-1}=1+\cfrac{2}{x-1}\),
即\(lnx-1=\cfrac{2}{x-1}\),由数转化到形,
在同一系中做出函数\(y=lnx-1\)和函数\(\cfrac{2}{x-1}\)的图像,
由图像可得,函数\(y=lnx-1\)和函数\(\cfrac{2}{x-1}\)的图像有两个交点,
故方程\(f(x)=\cfrac{x+1}{x-1}\)实数根的个数有两个。
(2)曲线\(y=f(x),y=g(x)\)公切线的条数有2个,证明如下:
设公切线与曲线\(y=f(x),y=g(x)\)分别相切于点\((m,lnm)\)和\((n,e^n)\),
由\(f'(x)=\cfrac{1}{x}\),\(g'(x)=e^{x}\)可得,
\(\begin{cases}\cfrac{1}{m}=e^n\\\cfrac{lnm-e^n}{m-n}=\cfrac{1}{m}\end{cases}\),
化简得,\((m-1)lnm=m+1\)
当\(m=1\)时,上式不成立;
当\(m\neq 1\)时,变形得到\(lnm=\cfrac{m+1}{m-1}\),
由(1)可知,方程\(lnm=\cfrac{m+1}{m-1}\)有2个实根,
即曲线\(y=f(x),y=g(x)\)公切线的条数有2个。
- 利用公切线证明不等式
(1)、求\(a、b\)的值和直线\(l\)的方程;
分析:一直线两曲线的公切线问题,同一法;
由题意,直线\(l\)与曲线\(C_1:y=f(x)\)切于点\((0,a)\),又\(f'(0)=a\),
故切线方程为\(y-a=a(x-0)\),即\(y=ax+a\);
与曲线\(C_2:y=g(x)\)切于点\((\cfrac{\pi}{2},1+\cfrac{\pi}{2}b)\),又\(g'(\cfrac{\pi}{2})=b\),
故切线方程为\(y-(1+\cfrac{\pi}{2}b)=b(x-\cfrac{\pi}{2})\),即\(y=bx+1\);
由同一法可知,\(a=b=1\),切线方程为\(y=x+1\)。
(2)、求证:\(ae^x+x^2-bx-sinx>0\)。
分析:证明时思路的预判,原不等式即\(e^x+x^2-x-sinx>0\)
思路一:令\(h(x)=e^x+x^2-x-sinx(x\in R)\),即需要说明\(h(x)_{min}>0\);
\(h'(x)=e^x+2x-1-cosx\);令\(m(x)=h'(x)\),
则\(m'(x)=e^x+2+sinx>0\)恒成立,故\(h'(x)\)在\(R\)上单调递增,
故此时我们想得到\(h'(x_0)>0\)或者\(h'(x_0)<0\)的可能性在\(x\in R\)时不存在了,
故要么放弃这一思路,要么考虑调整思路。
思路二:注意第一问的结论,函数\(f(x)=e^x+x^2\)和函数\(g(x)=x+sinx\)的公切线是直线\(y=x+1\)
故可以尝试这样转化,证明\(f(x)=e^x+x^2>x+1\),且证明\(g(x)=x+sinx<x+1\);
先尝试证明\(f(x)=e^x+x^2\ge x+1\),
作差令\(h(x)=e^x+x^2-x-1\),则\(h'(x)=e^x+2x-1\)
在同一个坐标系中做出函数\(y=e^x\)和函数\(y=1-2x\)的图像,由图像可得
\(x<0\)时,\(h'(x)<0\);\(x>0\)时,\(h'(x)>0\);
\(x=0\)时,\(h'(x)=0\);
故函数\(h(x)\)在\((-\infty,0)\)上单调递减,在\((0,+\infty)\)上单调递增,
故\(h(x)_{min}=h(0)=0\),故\(h(x)\ge 0\)恒成立,当且仅当\(x=0\)时取到等号;
再证明\(g(x)=x+sinx\leq x+1\);即证明\(sinx\leq 1\)
由三角函数的性质我们知道,这个不等式是恒成立的,当且仅当\(x=2k\pi+\cfrac{\pi}{2}(k\in Z)\)时取到等号;
综上所述,\(e^x+x^2\ge x+1\),\(x+1\ge x+sinx\),
故\(e^x+x^2>x+sinx\),等号不能同时取到,故此处取不等号。
即\(ae^x+x^2-bx-sinx>0\)。证毕。
双切线
说明:此类型涉及一曲线和两直线
分析:本题目如果总纠结要画出适合题意的图形,然后总结思路可能就浪费时间了。
可以这样考虑,设过曲线外的一点所引的两条切线的倾斜角分别是\(\alpha\)和\(\beta\),
则可知其对应的斜率为\(k_1=tan\alpha\)和\(k_2=tan\beta=tan(\pi-\alpha)=-tan\alpha\),故有\(k_1+k_2=0\)。
因此求解如下:
设过点\(A(1,0)\)的切线与曲线相切于点\((x_0,y_0)\),则由\(f'(x)=3x^2-a\),得到\(\begin{cases}k=f'(x_0)=3x_0^2-a\\y_0=x_0^3-ax_0+a\\y-y_0=(3x_0^2-a)(x-x_0)\end{cases}\),
又由点\(A(1,0)\)在切线上得到\(0-(x_0^3-ax_0+a)=(3x_0^2-a)(1-x_0)\),化简整理得到\(2x_0^3-3x_0^2=0\),解得\(x_0=0\)或者\(x_0=\cfrac{3}{2}\),
当\(x_0=0\)时,一条切线的斜率\(k_1=-a=tan\alpha\);
当\(x_0=\cfrac{3}{2}\)时,另一条切线的斜率\(k_2=\cfrac{27}{4}-a=tan\beta\),
由\(k_1+k_2=0\),得到\(\cfrac{27}{4}-2a=0\),解得\(a=\cfrac{27}{8}\),故选A。
分析:先做出分段函数\(f(x)\)的大致草图如下,
由于分段函数的图像关于\(x=a\)对称,点\(P(a,0)\)在对称轴上,故由\(\overrightarrow{PA}\cdot \overrightarrow{PB}\)的最小值为\(0\),
结合图像可知两个向量的夹角为锐角或直角,不可能为钝角,否则最小值为负值,
又由于图像是对称的,从点\(P\)出发的两条射线都和曲线相切时向量的夹角才会最大,
故说明向量的夹角为\(90^{\circ}\),且可知两条切线的斜率为\(k=\pm 1\),且可知\(\angle APO=45^{\circ}\),
那么怎么说明两个切点就是图中的\(A\),\(B\)两个点呢?
设切点\(A(x_0,y_0)\),则\(-e^{-x_0}=-1\),则\(x_0=0\),\(y_0=1\),故点\(A(0,1)\),从而可知\(a=1\),
由对称性也可知,\(B(2,1)\),到此完全说明\(A(0,1)\),\(B(2,1)\)为两个切点。
故\(f(x)_{min}=f(a)=f(1)=\cfrac{1}{e}\),故选\(D\)。
可转化类型
(1)、函数上的动点到直线的距离的最小值问题
比如:(2018陕西省二检第16题)
(2)、圆锥曲线上的动点到直线的距离的最小值问题,一般不转化为切线问题,而是用参数方程法,转化为函数的最小值问题
圆锥曲线是隐函数,所以其函数解析式不好写出来,不像那些显函数如\(y=2x+3\);
后记:这类题目,大多还可以使用“平行线法”这一思路。
(3)、单切线和公切线之间的关系:
单切线:涉及一个方程组和一条切线(简称“一组一线”),
公切线:涉及两个方程组和两条切线(简称“两组两线”),其中两条切线是同一条,使用同一法将其联系在一起。

 涉及切线的问题,主要关联的是导数知识和方程思想;总结单切线和公切线问题。
涉及切线的问题,主要关联的是导数知识和方程思想;总结单切线和公切线问题。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号