空间几何体中建系 | 空间直角坐标系
本博文旨在总结立体几何中常见几何体的建系方法和类型，比如正四面体中、正三棱柱中、四棱锥等中的建系方法，坐标计算方法等，便于学习。而且我们应该知道，当建立的坐标系不同时，计算的难度是不一样的。
前情概要
如果没有笛卡尔平面直角坐标系，那么涉及平面向量的问题只能用基向量的方法[形的角度]求解，不能用代数方法[数的角度]计算；同理如果没有空间直角坐标系的介入，立体几何中的问题也就只能从形的角度思考，而不能用代数方法[数的角度]来计算；所以建系的目的主要是想把有关形的问题，通过代数的方法计算解决；
本博文旨在总结立体几何中常见几何体的建系方法和类型，比如正四面体中、正三棱柱中、四棱锥等中的建系方法，坐标计算方法等，便于学习。而且我们应该知道，当建立的坐标系不同时，计算的难度是不一样的。
相关阅读
建系汇总
✍️ 正四面体中的建系，建立空间直角坐标系；
解法1️⃣ ：空间向量法，如图所示，\(PF\perp\)面\(ABC\)，\(F\)为\(\Delta ABC\)的中心，
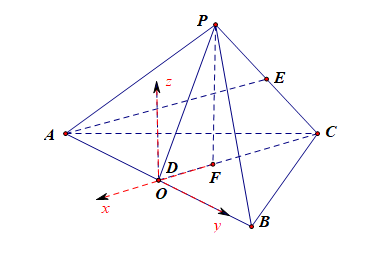
以点\(D\)为坐标原点，以\(DF\)、\(DB\)以及与\(FP\)平行的直线分别为\(x\)，\(y\)，\(z\)轴建立如图所示的空间直角坐标系，
令正四面体的棱长为\(2\)，则得到以下点的空间坐标
\(D(0，0，0)\)，\(A(0，-1，0)\)，\(B(0，1，0)\)，
\(C(-\sqrt{3}，0，0)\)，\(P(-\cfrac{\sqrt{3}}{3}，0，\cfrac{2\sqrt{6}}{3})\)，\(E(-\cfrac{2\sqrt{3}}{3}，0，\cfrac{\sqrt{6}}{3})\)，
则有\(\overrightarrow{PD}=(\cfrac{\sqrt{3}}{3}，0，-\cfrac{2\sqrt{6}}{3})\)；\(\overrightarrow{AE}=(-\cfrac{2\sqrt{3}}{3}，1，\cfrac{\sqrt{6}}{3})\)；
令异面直线\(PD\)和\(AE\)的夹角为\(\theta\)，则有\(cos\theta\)
\(=\cfrac{|\cfrac{\sqrt{3}}{3}\cdot (-\cfrac{2\sqrt{3}}{3})+0\cdot 1+(-\cfrac{2\sqrt{6}}{3}\cdot \cfrac{\sqrt{6}}{3})|}{\sqrt{(\cfrac{\sqrt{3}}{3})^2+(-\cfrac{2\sqrt{6}}{3})^2}\cdot \sqrt{(-\cfrac{2\sqrt{3}}{3})^2+1^2+(\cfrac{\sqrt{6}}{3})^2}}=\cfrac{2}{3}\)。
说明：向量的夹角范围为\([0，\pi]\)，两异面直线的夹角范围\([0，\cfrac{\pi}{2}]\)。
解法2️⃣ ：立体几何法，先作再证后算。思路：异面直线所成的角，一般是经过平移，使其相交，构建三角形来计算。
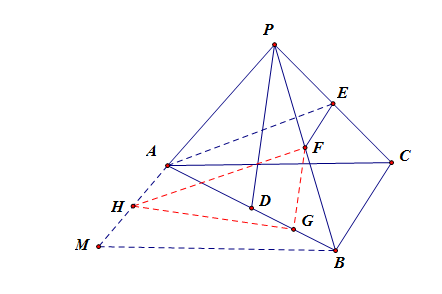
过点\(A\)做\(AM//BC\)，过点\(B\)做\(BM//AC\)交\(AM\)于点\(M\)，
点\(F\)、\(H\)、\(G\)分别是线段\(PB\)、\(AM\)、\(BD\)的中点，连接\(HF\)、\(FG\)、\(HG\)，
则有 \(EF\;\;{}_{=}^{//}AH\)，则\(AE//FH\)，又\(PD//FG\)，故\(\angle HFG\)为两条异面直线所成的角。
设正四面体的棱长为\(2\)，则\(AE=FH=PD=\sqrt{3}\)，\(FG=\cfrac{\sqrt{3}}{2}\)；
又在\(\Delta AHG\)中，\(AH=1\)，\(AG=\cfrac{3}{2}\)，\(\angle HAG=60^\circ\)，
由余弦定理可知，\(HG=\cfrac{\sqrt{7}}{2}\)，
在\(\Delta HFG\)中，\(HF=\sqrt{3}\)，\(FG=\cfrac{\sqrt{3}}{2}\)，\(HG=\cfrac{\sqrt{7}}{2}\)，
由余弦定理可知\(cos\angle HFG=\cfrac{2}{3}\)。
✍️ 四棱锥中的建系，建立空间直角坐标系；
(1).证明：\(BD\perp\) 平面 \(PAC\)；
证明：由于侧棱 \(PA\perp\) 底面\(ABCD\)，\(BD\subsetneqq\) 底面 \(ABCD\)，故 \(PA\perp BD\)；
又由于 \(AC\) 和 \(BD\) 是正方形的对角线，则 \(AC\perp BD\)，
则\(BD\perp AC\)，\(BD\perp PA\)，\(PA\cap AC=A\)，
\(PA\subsetneqq\) 平面 \(PAC\)，\(AC\subsetneqq\) 平面 \(PAC\)，
故 \(BD\perp\) 平面 \(PAC\)；
(2).求二面角 \(C-BD-Q\) 的余弦值。【此题目包含平面的法向量的详细求解方法】
解法1️⃣ ：思路一，空间向量法，由题可知，\(AB\)、\(AP\)、\(AD\) 两两垂直，以 \(A\) 为坐标原点，分别以 \(AB\)、\(AD\)、\(AP\) 所在直线为 \(x\)，\(y\)，\(z\) 轴建立空间直角坐标系，如图所示。
则点\(B(2，0，0)\)，\(C(2，2，0)\)，\(D(0，2，0)\)，\(Q(0，0，1)\)，
所以 \(\overrightarrow{BD}=(-2，2，0)\)，\(\overrightarrow{BQ}=(-2，0，1)\)，
设平面 \(BDQ\) 的法向量为 \(\vec{m}=(x，y，z)\)，[1] 则有
即\(\begin{cases}-2x+2y=0\\-2x+z=0\end{cases}\)，可以取 \(\vec{m}=(1，1，2)\) 由于得到的方程组是不定方程组，应该有无穷多组解，此处只关注其存在性，故可以通过赋值来得到这个不定方程组的解。比如考虑到运算的简单，我们令\(x=1\)，则得到\(y=1\)，\(z=2\)，则 \(\vec{m}\)\(=\)\((1,1,2)\)
平面 \(BDC\) 的法向量为 \(\vec{n}=(0，0，1)\)可以用同样的思路和方法来求解法向量，当然也可以用更快捷的方法，比如我们注意到平面 \(BDC\) 也就是平面 \(ABCD\)，故其法向量可以取 \(z\) 轴所在直线的方向向量，为简单起见，取为\((0,0,1)\)，
设二面角 \(C-BD-Q\) 的平面角为 \(\theta\)，由图可知 \(\theta\) 为钝角1、平面角为锐角或钝角是直观观察得到的；2、\(<\vec{m},\vec{n}>\) 可能为锐角，也可能为钝角，故使用 \(|\cos<\vec{m},\vec{n}>|\) 来限制，又由于平面角为钝角，故\(cos\theta\)\(=\)\(-|cos<\vec{m}，\vec{n}>|\)，则有
所以二面角 \(C-BD-Q\) 的余弦值为 \(-\cfrac{\sqrt{6}}{3}\) .
解法2️⃣ ：思路二，定义法，求解步骤为[作---证---算]；令 \(AC\) 与 \(BD\) 的交点为 \(E\)，连结 \(QE\) 和 \(QC\)，则 \(\angle QEC\) 为所求二面角的平面角[一作]，理由如下：
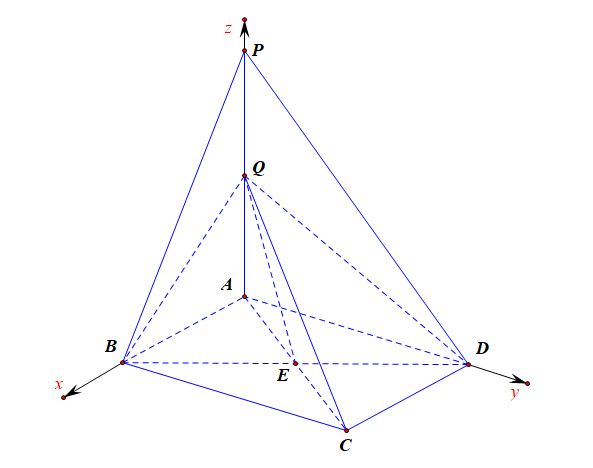
由于底面 \(ABCD\) 是正方形，故 \(EC\perp BD\)，又由于 \(BD\perp AC\)，\(BD\perp AP\)，则 \(BD\perp\) 平面 \(QAC\)，\(QE\subsetneqq\) 平面 \(QAC\)，故 \(BD\perp QE\)，到此满足条件 \(QE\perp BD\)，又 \(EC\perp BD\)，则 \(\angle QEC\) 为所求二面角 \(C-BD-Q\) 的平面角[二证] .
由题目可知， \(ABCD\) 是边长为 \(2\) 的正方形，则 \(AC=2\sqrt{2}\)，\(EC=\sqrt{2}\)，又 \(QA=1\)，则由勾股定理可知 \(QE=\sqrt{3}\)， \(QC=3\)，
到此可知，在 \(\triangle QEC\) 中，\(EC=\sqrt{2}\)，\(QE=\sqrt{3}\)，\(QC=3\)，利用余弦定理可知，
\(\cos\angle QEC\)\(=\)\(\cfrac{EC^2+QE^2-QC^2}{2\times EC\times QE}\)\(=\)\(\cfrac{2+3-9}{2\times\sqrt{2}\times\sqrt{3}}\)\(=\)\(-\cfrac{\sqrt{6}}{3}\)[三算] .
所以二面角 \(C-BD-Q\) 的余弦值为 \(-\cfrac{\sqrt{6}}{3}\) .
[解后反思]：思路二主要使用在高一阶段，学生初次学习了二面角，还没有学习空间向量，这种方法的优越性在于能明白无误的做出来平面角，知道它在图形中的什么地方，也能准确的计算出来，思路一主要使用在学生学习了空间向量之后，这种方法即使你不知道所求的平面角如何作，也能进行相关的计算，不足之处是学生对二面角的平面角在哪里，长什么样子都可能糊里糊涂，所以这几年有高校的老师强烈建议取消思路一的教学，强制使用思路二，也不无道理。
✍️ 正三棱柱中的建系，建立空间直角坐标系；
解法1️⃣ ：空间向量法，第一种建系方式；以点\(A\)为坐标原点，以\(AC\)，\(AA_1\)分别为\(y\)、\(z\)轴，以和\(AC\)垂直的直线为\(x\)轴，建立如图所示的空间直角坐标系，
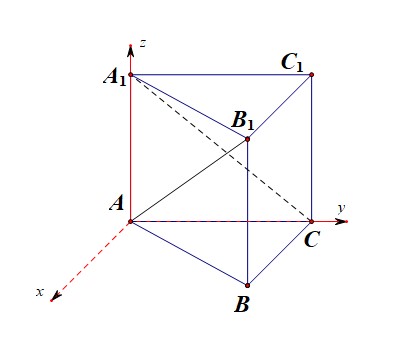
则\(A(0，0，0)\)，\(B(\sqrt{3}，1，0)\)，\(A_1(0，0，2)\)，\(B_1(\sqrt{3}，1，2)\)，\(C(0，2，0)\)，
\(\overrightarrow{AB_1}=(\sqrt{3}，1，2)\)，\(\overrightarrow{A_1C}=(0，2，-2)\)，且线线角的范围是\([0，\cfrac{\pi}{2}]\)，
故所求角的余弦值为\(|cos<\overrightarrow{AB_1}，\overrightarrow{A_1C}>|=\cfrac{|1\times 2+2\times(-2)|}{\sqrt{8}\times\sqrt{8}}=\cfrac{1}{4}\)。故选\(C\)。
解法2️⃣ ：空间向量法，第二种建系方式；以\(BN\)的中点为坐标原点建立如图所示的空间直角坐标系，
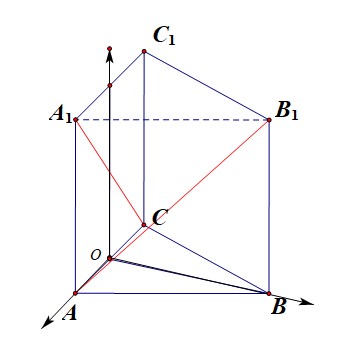
则\(A(1，0，0)\)，\(B(0，\sqrt{3}，0)\)，\(C(-1，0，0)\)，\(A_1(1，0，2)\)，\(B_1(0，\sqrt{3}，2)\)，\(C_1(-1，0，2)\)，
\(\overrightarrow{AB_1}=(-1，\sqrt{3}，2)\)，\(\overrightarrow{A_1C}=(-2，0，-2)\)，且线线角的范围是\([0，\cfrac{\pi}{2}]\)，
故所求角的余弦值为\(|cos<\overrightarrow{AB_1}，\overrightarrow{A_1C}>|=\cfrac{|-1\times (-2)+\sqrt{3}\times 0+2\times(-2)|}{\sqrt{8}\times\sqrt{8}}=\cfrac{1}{4}\)。故选\(C\)。
解法3️⃣ ：立体几何法，补体平移法，将正三棱柱补体为一个底面为菱形的直四棱柱，连结\(B_1D\)，则\(B_1D//A_1C\)，
故异面直线\(AB_1\)与\(CA_1\)所成角，即转化为共面直线\(AB_1\)与\(B_1D\)所成的角\(\angle AB_1D\)，连结\(AD\)，
在\(\Delta AB_1D\)中，\(AB=AA_1=2\)，可得\(AB_1=B_1D=2\sqrt{2}\)，\(AD=2\sqrt{3}\)，
由余弦定理可知，\(cos\angle AB_1D=\cfrac{(2\sqrt{2})^2+(2\sqrt{2})^2-(2\sqrt{3})^2}{2\times 2\sqrt{2}\times 2\sqrt{3}}=\cfrac{1}{4}\)，
故所求为\(\cfrac{1}{4}\)，故选\(C\)。
✍️ 三棱锥中的建系，建立空间直角坐标系；
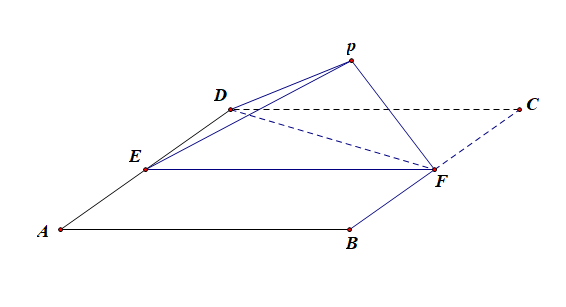
(1).证明：平面\(PEF\perp\)平面\(ABFD\)；
证明：由已知可得，\(BF\perp PF\)，\(BF\perp EF\)，
又\(PF\cap EF=F\)，\(PF\subseteq\)平面\(PEF\)，\(EF\subseteq\)平面\(PEF\)，
所以\(BF\perp\)平面\(PEF\)，又\(BF\subseteq\)平面\(ABFD\)，
所以平面\(PEF\perp\)平面\(ABFD\)；
(2).求\(DP\)与平面\(ABFD\)所成角的正弦值。
解：作\(PH\perp EF\)，垂足为\(H\)，由(1)得，\(PH\perp\)平面\(ABFD\)，以\(H\)为坐标原点，\(\overrightarrow{HF}\)的方向为\(y\)轴正方向，\(|\overrightarrow{BF}|\)为单位长，建立如图所示的空间直角坐标系\(H-xyz\)，
由(1)得到，\(DE\perp PE\)，又\(DP=2\)，\(DE=1\)，所以\(PE=\sqrt{3}\)，
又\(PF=1\)，\(EF=2\)，所以\(PE\perp PF\)，可得\(PH=\cfrac{\sqrt{3}}{2}\)，\(EH=\cfrac{3}{2}\)，
则\(H(0，0，0)\)，\(P(0，0，\cfrac{\sqrt{3}}{2})\)，\(D(-1，-\cfrac{3}{2}，0)\)，
则\(\overrightarrow{DP}=(1，\cfrac{3}{2}，\cfrac{\sqrt{3}}{2})\)，\(\overrightarrow{HP}=(0，0，\cfrac{\sqrt{3}}{2})\)为平面\(ABFD\)的法向量，
设\(DP\)与平面\(ABFD\)所成角为\(\theta\)，则\(sin\theta=|cos<\overrightarrow{HP}，\overrightarrow{DP}>|=|\cfrac{\overrightarrow{HP}\cdot \overrightarrow{DP}}{|\overrightarrow{HP}||\overrightarrow{DP}|}|=\cfrac{\frac{3}{4}}{\sqrt{3}}=\cfrac{\sqrt{3}}{4}\)，
所以\(DP\)与平面\(ABFD\)所成角的正弦值为\(\cfrac{\sqrt{3}}{4}\)。
✍️ 长方体中的建系，建立空间直角坐标系；
(1).证明：\(BE\perp\)平面\(EB_1C_1\)；
分析：需要证明线面垂直，往往先要转化为证明线线垂直；
解析：由已知\(B_1C_1\perp\)平面\(ABB_1A_1\)，\(BE\subset\)平面\(ABB_1A_1\)，故\(B_1C_1\perp BE\)，
又\(BE\perp EC_1\)，\(B_1C_1\subset\)平面\(EB_1C_1\)，\(EC_1\subset\)平面\(EB_1C_1\)，\(B_1C_1\cap EC_1=C_1\)，
故\(BE\perp\)平面\(EB_1C_1\)；
(2).若\(AE=A_1E\)，求二面角\(B-EC-C_1\)的正弦值；
解析：由(1)知道\(\angle BEB_1=90^{\circ}\)，由题设可知\(Rt\triangle ABE\cong Rt\triangle A_1B_1E\)，所以\(\angle AEB=45^{\circ}\)，故\(AE=AB\)，\(AA_1=2AB\)，
以\(D\)为坐标原点，\(\overrightarrow{DA}\)的方向为\(x\)轴的正方向，\(|\overrightarrow{DA}|\)为单位长，建立如图所示的空间直角坐标系\(D-xyz\)，则\(C(0，1，0)\)，\(B(1，1，0)\)，\(C_1(0，1，2)\)，\(E(1，0，1)\)，\(\overrightarrow{CB}=(1，0，0)\)，\(\overrightarrow{CE}=(1，-1，1)\)，\(\overrightarrow{CC_1}=(0，0，2)\)，
设平面\(EBC\)的法向量\(\vec{n}=(x，y，z)\)，
则\(\left\{\begin{array}{l}{\overrightarrow{CB}\cdot \vec{n}=0}\\{\overrightarrow{CE}\cdot \vec{n}=0}\end{array}\right.\)，即\(\left\{\begin{array}{l}{x=0}\\{x-y+z=0}\end{array}\right.\)，所以可以赋值取\(\vec{n}=(0，-1，-1)\)，
设平面\(ECC_1\)的法向量\(\vec{m}=(x，y，z)\)，
则\(\left\{\begin{array}{l}{\overrightarrow{CC_1}\cdot \vec{m}=0}\\{\overrightarrow{CE}\cdot \vec{m}=0}\end{array}\right.\)，即\(\left\{\begin{array}{l}{2z=0}\\{x-y+z=0}\end{array}\right.\)，所以可以赋值取\(\vec{m}=(1，1，0)\)，
于是，\(cos<\vec{n}，\vec{m}>=\cfrac{\vec{n}\cdot\vec{m}}{|\vec{n}||\vec{m}|}=-\cfrac{1}{2}\)，
即\(<\vec{n}，\vec{m}>=120^{\circ}\)，所以，二面角\(B-EC-C_1\)的正弦值为\(\cfrac{\sqrt{3}}{2}\)。
解后反思：当然，本题目同样可用点\(C\)做为坐标原点来建立坐标系。
✍️ 建系不难，难点在点的坐标确定，新考向；
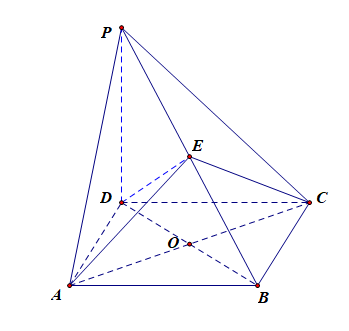
（1）求证：平面\(EAC\perp\) 平面\(BPD\);
分析：由于\(PD\perp\)平面\(ABCD\)，所以\(PD\perp AC\)，
由于四边形\(ABCD\)是菱形，所以\(BD\perp AC\)，
又由于\(BD\cap PD=D\)，所以\(AC\perp\) 平面\(PBD\)，
又由于\(AC\subseteq\) 平面\(AEC\)，所以平面\(EAC\perp\) 平面\(BPD\);
（2）若\(E\)为\(PB\)的中点，\(AC=2\)，\(BD=2\sqrt{3}\)，且二面角\(A-PB-D\)的余弦值为\(\cfrac{\sqrt{21}}{7}\)，求四棱锥\(P-ABCD\)的体积；
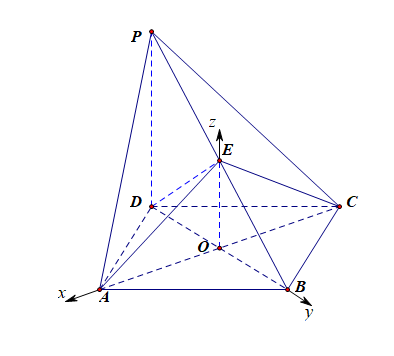
分析：连接\(OE\)，在\(\triangle PBD\)中，\(EO//PD\)，所以\(EO\perp\)平面\(ABCD\)，分别以\(OA\)，\(OB\)，\(OE\)所在直线为\(x\)轴，\(y\)轴，\(z\)轴建立如图所示的空间直角坐标系，设\(PD=t\)，则\(A(1，0，0)\)，\(B(0，\sqrt{3}，0)\)，\(C(-1，0，0)\)，\(E(0，0，\cfrac{t}{2})\)，\(P(0，-\sqrt{3}，t)\)，
设平面\(PAB\)的一个法向量为\(\vec{n}=(x，y，z)\)，
则\(\left\{\begin{array}{l}{\vec{n}\cdot \overrightarrow{AB}=-x+\sqrt{3}y=0}\\{\vec{n}\cdot \overrightarrow{AP}=-x-\sqrt{3}y+tz=0}\end{array}\right.\) 令\(y=1\)，得到\(\vec{n}=(\sqrt{3}，1，\cfrac{2\sqrt{3}}{t})\)，
平面\(PBD\)的法向量\(\vec{m}=(1，0，0)\)，
由于二面角\(A-PB-D\)的余弦值为\(\cfrac{\sqrt{21}}{7}\)，则\(|cos<\vec{m}，\vec{n}>|=\cfrac{\sqrt{3}}{\sqrt{4+\frac{12}{t^2}}}=\cfrac{\sqrt{21}}{7}\)
解得\(t=2\)或\(t=-2\)(舍去)，故四棱锥\(P-ABCD\)的体积为\(V=\cfrac{1}{3}\times \cfrac{1}{2}\times 2\times 2\sqrt{3}\times 2=\cfrac{4\sqrt{3}}{3}\)；
✍️ 斜棱柱建系问题
斜棱柱这类建系，主要难点是分析“空中”的点的坐标。空中点坐标可以从以下几方面思考:
1、如果是菱形，多是60°角菱形，则可以通过菱形分割成两个等边三角形，再借助“等边三角形的中线就是高”，寻找 \(z\) 轴
2、让空中点垂直砸下来(落下来，寻找投影)，投影点坐标以及下落的高度
3、借助向量相等，寻找空中点所在线段的向量对应的底面相等向量，即可计算出空中点的坐标
4、结合已知的线面垂直通过做垂线，来得出线面垂直
✍️ 斜棱锥建系问题基础知识
斜面型棱锥， 不容易找到垂面和垂线，多采用投影法来建系：一般从棱锥顶点向下底面做垂线，通过题中条件，寻找并计算出三棱锥的高，在底面寻找一对互相垂直的线作为 \(x\)、\(y\) 轴来建立坐标系
如果一条直线和平面内的两条相交直线都垂直，则该直线和平面垂直。 ↩︎
浙公网安备 33010602011771号