各种角的求解

前言

• 常见的需要求解的角有：异面直线所成的角，线面角，二面角，向量的夹角；
• 相关阅读：高中数学中常见角的范围表示

线线角

【2017凤翔中学高三第三次月考第10题】【异面直线所成的角】长方体\(ABCD-A_1B_1C_1D_1\)中，\(AB\)\(=\)\(AA_1\)\(=\)\(2\)，\(AD=1\)，则异面直线 \(BC_1\) 与 \(AC\) 所成的角的余弦值是多少？

法1：立体几何法，基本求解步骤：①作：作出所要求的角；②证：证明所作的角即为所求的角；③算：计算所作角的某种三角值；

思路：将两条异面直线平移至一个三角形中，然后解三角形得到。

将\(BC_1\)平移到\(AD_1\)，联结\(CD_1\)，则\(\angle CAD_1\)为两条异面直线所成的角，

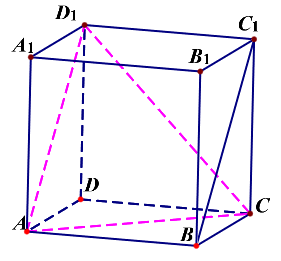
在\(\Delta ACD_1\)中，可知\(AC=\sqrt{5}\)，\(AD_1=\sqrt{5}\)，\(CD_1=2\sqrt{2}\)，

由余弦定理可知\(cos\angle CAD_1=\cfrac{(\sqrt{5})^2+(\sqrt{5})^2-(2\sqrt{2})^2}{2\cdot \sqrt{5}\cdot \sqrt{5}}=\cfrac{1}{5}\)；

法2：空间向量法，

以点\(D\)为坐标原点，分别以\(DA、DC、DD_1\)所在的直线为\(x、y、z\)轴建立如图所示的直角坐标系，

则点\(D(0，0，0)\)，\(A(1，0，0)\)，\(C(0，2，0)\)，\(B(1，2，0)\)，\(D_1(0，0，2)\)，\(A_1(1，0，2)\)，\(B_1(1，2，2)\)，\(C_1(0，2，2)\)，

故\(\overrightarrow{BC_1}=(-1，0，2)\)，\(\overrightarrow{AC}=(-1，2，0)\)，

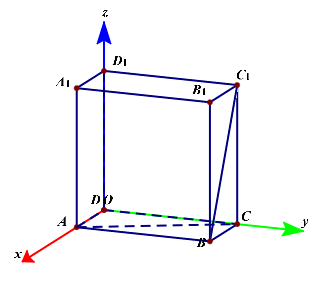
设两条异面直线所成的角为\(\theta\)，则\(cos\theta=|cos<\overrightarrow{BC_1}，\overrightarrow{AC}>|=\cfrac{(-1)\times(-1)+0\times2+2\times 0}{\sqrt{(-1)^2+0^2+2^2}\times\sqrt{(-1)^2+2^2+0^2}}=\cfrac{1}{5}\)。

备注：两条异面直线所成角的范围\([0，\cfrac{\pi}{2}]\)，两个向量所成角的范围\([0，\pi]\)。

【2019届宝鸡市高三理科数学质检Ⅰ第10题】已知正三棱柱\(ABC-A_1B_1C_1\)中，\(AB=AA_1=2\)，则异面直线\(AB_1\)与\(CA_1\)所成角的余弦值为【】

$A.0$ $B.-\cfrac{1}{4}$ $C.\cfrac{1}{4}$ $D.\cfrac{1}{2}$

【法1-1】空间向量法，第一种建系方式；以点\(A\)为坐标原点，以\(AC\)，\(AA_1\)分别为\(y\)、\(z\)轴，以和\(AC\)垂直的直线为\(x\)轴，建立如图所示的空间直角坐标系，

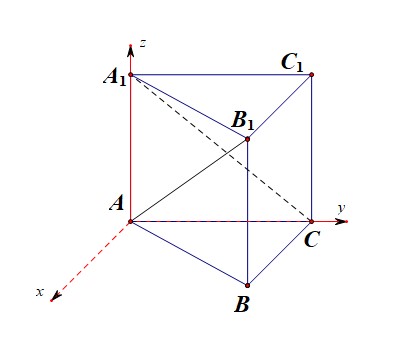
则\(A(0，0，0)\)，\(B(\sqrt{3}，1，0)\)，\(A_1(0，0，2)\)，\(B_1(\sqrt{3}，1，2)\)，\(C(0，2，0)\)，

\(\overrightarrow{AB_1}=(\sqrt{3}，1，2)\)，\(\overrightarrow{A_1C}=(0，2，-2)\)，且线线角的范围是\([0，\cfrac{\pi}{2}]\)，

故所求角的余弦值为\(|cos<\overrightarrow{AB_1}，\overrightarrow{A_1C}>|=\cfrac{|1\times 2+2\times(-2)|}{\sqrt{8}\times\sqrt{8}}=\cfrac{1}{4}\)。故选\(C\)。

【法1-2】空间向量法，第二种建系方式；以\(BN\)的中点为坐标原点建立如图所示的空间直角坐标系，

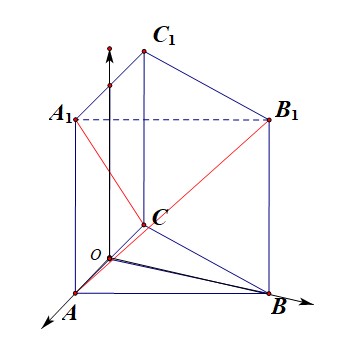
则\(A(1，0，0)\)，\(B(0，\sqrt{3}，0)\)，\(C(-1，0，0)\)，\(A_1(1，0，2)\)，\(B_1(0，\sqrt{3}，2)\)，\(C_1(-1，0，2)\)，

\(\overrightarrow{AB_1}=(-1，\sqrt{3}，2)\)，\(\overrightarrow{A_1C}=(-2，0，-2)\)，且线线角的范围是\([0，\cfrac{\pi}{2}]\)，

故所求角的余弦值为\(|cos<\overrightarrow{AB_1}，\overrightarrow{A_1C}>|=\cfrac{|-1\times (-2)+\sqrt{3}\times 0+2\times(-2)|}{\sqrt{8}\times\sqrt{8}}=\cfrac{1}{4}\)。故选\(C\)。

【法2】：立体几何法，补体平移法，将正三棱柱补体为一个底面为菱形的直四棱柱，连结\(B_1D\)，则\(B_1D//A_1C\)，

故异面直线\(AB_1\)与\(CA_1\)所成角，即转化为共面直线\(AB_1\)与\(B_1D\)所成的角\(\angle AB_1D\)，连结\(AD\)，

在\(\Delta AB_1D\)中，\(AB=AA_1=2\)，可得\(AB_1=B_1D=2\sqrt{2}\)，\(AD=2\sqrt{3}\)，

由余弦定理可知，\(cos\angle AB_1D=\cfrac{(2\sqrt{2})^2+(2\sqrt{2})^2-(2\sqrt{3})^2}{2\times 2\sqrt{2}\times 2\sqrt{3}}=\cfrac{1}{4}\)，

故所求为\(\cfrac{1}{4}\)，故选\(C\)。

【2019届高三理科数学三轮模拟试题】在长方体\(ABCD-A_1B_1C_1D_1\)中，已知直线\(BD\)与平面\(ADD_1A_1\)所成角的正切值为\(2\)，直线\(BD_1\)与平面\(ABCD\)所成角的正弦值为\(\cfrac{2}{3}\)，则异面直线\(CD_1\)与\(BD_1\)所成角的余弦值为【】

$A.\cfrac{\sqrt{10}}{5}$ $B.\cfrac{3\sqrt{5}}{10}$ $C.\cfrac{\sqrt{55}}{10}$ $D.\cfrac{\sqrt{15}}{5}$

分析：如图所示，直线\(BD\)与平面\(ADD_1A_1\)所成角的为\(\angle BDA\)，则由\(tan\angle BDA=2\)，可以设\(AB=2k\)，\(AD=k\)，则\(BD=\sqrt{5}k\)，直线\(BD_1\)与平面\(ABCD\)所成角的为\(\angle D_1BD\)，则由\(sin\angle D_1BD=\cfrac{2}{3}\)，可以设\(DD_1=2m\)，\(BD_1=3m\)，则\(BD=\sqrt{5}m\)，

故可以令\(m=k=1\)，则长方体的三维\(AB=2\)，\(AD=1\)，\(DD_1=2\)，接下来的思路可以有两个：

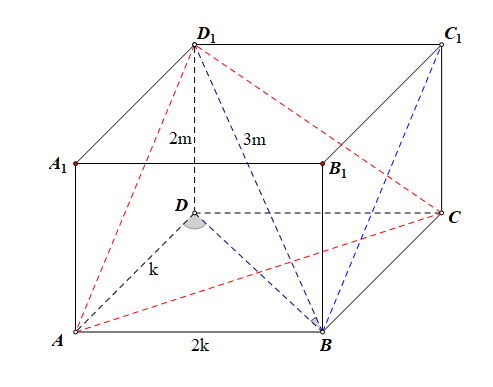
思路1：平移法，将异面直线\(CD_1\)与\(BD_1\)通过平移放置到同一个三角形\(\triangle AVD_1\)中，这样\(AC=\sqrt{5}\)，\(AD_1=\sqrt{5}\)，\(CD_1=2\sqrt{2}\)，则异面直线\(CD_1\)与\(BD_1\)所成的角即为\(\angle AD_1C\)，由余弦定理可知\(cos \angle AD_1C=\cfrac{\sqrt{10}}{5}\).故选\(A\).

思路2：空间向量法，不作平移，直接利用直线的方向向量的夹角来求解；

如图，正四面体\(P-ABC\)中，\(D\)、\(E\)分别是\(AB\)和\(PC\)的中点，则直线\(AE\)与\(PD\)所成角的余弦值是多少？

法1：空间向量法，如图所示，\(PF\perp\)面\(ABC\)，\(F\)为\(\Delta ABC\)的中心，

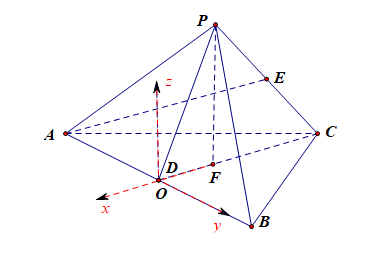
以点\(D\)为坐标原点，以\(DF\)、\(DB\)以及与\(FP\)平行的直线分别为\(x\)，\(y\)，\(z\)轴建立如图所示的空间直角坐标系，

令正四面体的棱长为\(2\)，则得到以下点的空间坐标

\(D(0，0，0)\)，\(A(0，-1，0)\)，\(B(0，1，0)\)，

\(C(-\sqrt{3}，0，0)\)，\(P(-\cfrac{\sqrt{3}}{3}，0，\cfrac{2\sqrt{6}}{3})\)，\(E(-\cfrac{2\sqrt{3}}{3}，0，\cfrac{\sqrt{6}}{3})\)，

则有\(\overrightarrow{PD}=(\cfrac{\sqrt{3}}{3}，0，-\cfrac{2\sqrt{6}}{3})\)；\(\overrightarrow{AE}=(-\cfrac{2\sqrt{3}}{3}，1，\cfrac{\sqrt{6}}{3})\)；

令异面直线\(PD\)和\(AE\)的夹角为\(\theta\)，则有\(cos\theta\)

\(=\cfrac{|\cfrac{\sqrt{3}}{3}\cdot (-\cfrac{2\sqrt{3}}{3})+0\cdot 1+(-\cfrac{2\sqrt{6}}{3}\cdot \cfrac{\sqrt{6}}{3})|}{\sqrt{(\cfrac{\sqrt{3}}{3})^2+(-\cfrac{2\sqrt{6}}{3})^2}\cdot \sqrt{(-\cfrac{2\sqrt{3}}{3})^2+1^2+(\cfrac{\sqrt{6}}{3})^2}}=\cfrac{2}{3}\)。

说明：向量的夹角范围为\([0，\pi]\)，两异面直线的夹角范围\([0，\cfrac{\pi}{2}]\)。

法2：立体几何法，先作再证后算。

思路：异面直线所成的角，一般是经过平移，使其相交，构建三角形来计算。

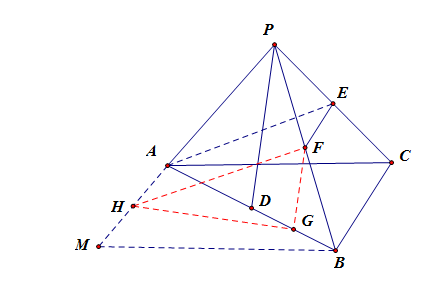
过点\(A\)做\(AM//BC\)，过点\(B\)做\(BM//AC\)交\(AM\)于点\(M\)，

点\(F\)、\(H\)、\(G\)分别是线段\(PB\)、\(AM\)、\(BD\)的中点，连接\(HF\)、\(FG\)、\(HG\)，

则有 \(EF\stackrel{//}{=}AH\) ，则\(AE//FH\)，又\(PD//FG\)，故\(\angle HFG\)为两条异面直线所成的角。

设正四面体的棱长为\(2\)，则\(AE=FH=PD=\sqrt{3}\)，\(FG=\cfrac{\sqrt{3}}{2}\)；

又在\(\Delta AHG\)中，\(AH=1\)，\(AG=\cfrac{3}{2}\)，\(\angle HAG=60^\circ\)，

由余弦定理可知，\(HG=\cfrac{\sqrt{7}}{2}\)，

在\(\Delta HFG\)中，\(HF=\sqrt{3}\)，\(FG=\cfrac{\sqrt{3}}{2}\)，\(HG=\cfrac{\sqrt{7}}{2}\)，

由余弦定理可知\(cos\angle HFG=\cfrac{2}{3}\)。

线面角

【2018年全国卷Ⅰ第18题】如图，四边形\(ABCD\)为正方形，\(E\)，\(F\)分别为\(AD\)，\(BC\)的中点，以\(DF\)为折痕把\(\triangle DFC\)折起，使点\(C\)到达点\(P\)的位置，且\(PF\perp BF\)，

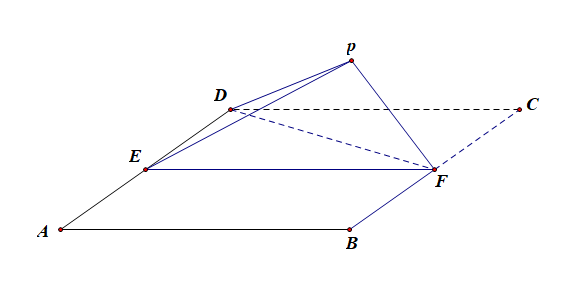
(1).证明：平面\(PEF\perp\)平面\(ABFD\)；

证明：由已知可得，\(BF\perp PF\)，\(BF\perp EF\)，

又\(PF\cap EF=F\)，\(PF\subseteq\)平面\(PEF\)，\(EF\subseteq\)平面\(PEF\)，

所以\(BF\perp\)平面\(PEF\)，又\(BF\subseteq\)平面\(ABFD\)，

所以平面\(PEF\perp\)平面\(ABFD\)；

(2).求\(DP\)与平面\(ABFD\)所成角的正弦值。

解：作\(PH\perp EF\)，垂足为\(H\)，由(1)得，\(PH\perp\)平面\(ABFD\)，以\(H\)为坐标原点，\(\overrightarrow{HF}\)的方向为\(y\)轴正方向，\(|\overrightarrow{BF}|\)为单位长，建立如图所示的空间直角坐标系\(H-xyz\)，

由(1)得到，\(DE\perp PE\)，又\(DP=2\)，\(DE=1\)，所以\(PE=\sqrt{3}\)，

又\(PF=1\)，\(EF=2\)，所以\(PE\perp PF\)，可得\(PH=\cfrac{\sqrt{3}}{2}\)，\(EH=\cfrac{3}{2}\)，

则\(H(0，0，0)\)，\(P(0，0，\cfrac{\sqrt{3}}{2})\)，\(D(-1，-\cfrac{3}{2}，0)\)，

则\(\overrightarrow{DP}=(1，\cfrac{3}{2}，\cfrac{\sqrt{3}}{2})\)，\(\overrightarrow{HP}=(0，0，\cfrac{\sqrt{3}}{2})\)为平面\(ABFD\)的法向量，

设\(DP\)与平面\(ABFD\)所成角为\(\theta\)，则\(sin\theta=|cos<\overrightarrow{HP}，\overrightarrow{DP}>|=|\cfrac{\overrightarrow{HP}\cdot \overrightarrow{DP}}{|\overrightarrow{HP}||\overrightarrow{DP}|}|=\cfrac{\frac{3}{4}}{\sqrt{3}}=\cfrac{\sqrt{3}}{4}\)，

所以\(DP\)与平面\(ABFD\)所成角的正弦值为\(\cfrac{\sqrt{3}}{4}\)。

【2024高一训练题目】如图，在正方体 \(ABCD-A_1B_1C_1D_1\) 中，点 \(F\) 是线段 \(BC_1\) 上的动点，则直线 \(A_1F\) 与平面 \(BDC_1\) 所成的最大角的余弦值为___________.

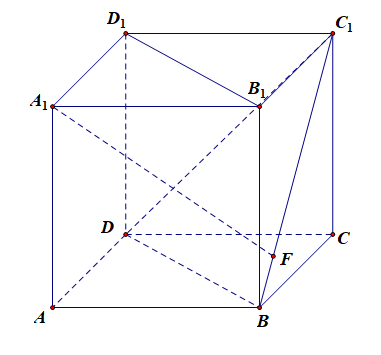
解：如图所示，利用正方体中储备的知识 ^[1]很容易想到，连接 \(A_1C\)，则可知体对角线 \(A_1C\perp\) 平面 \(BC_1D\)，令垂足为点 \(O\)，连接 \(OF\) ，则直线 \(A_1F\) 与平面 \(BDC_1\) 所成的角为 \(\angle A_1FO\)，为了求 \(\angle A_1FO\) 的最大值，可以考虑两个角度：其一，从形上思考，在等边 \(\triangle DC_1B\) 中，当动点 \(F\) 靠近点 \(B\) 或点 \(C_1\) 时 \(\angle A_1FO\) 越来越小(可以借助极端的情形思考，让线段 \(BC_1\) 非常长，则角的顶点就近乎在无限远处，其大小就接近 0 了)，那么在线段的中点位置时[其实是 \(OF\perp BC_1\) 时，为什么这样可以从思路二中得到解答和印证]，\(\angle A_1FO\) 达到最大，为便于计算，令 \(AB=1\)，则 \(A_1C=\sqrt{3}\)，\(A_1O\)\(=\)\(\cfrac{2}{3}A_1C\)\(=\)\(\cfrac{2\sqrt{3}}{3}\)，\(BD\)\(=\)\(\sqrt{2}\)，则 \(BF\)\(=\)\(\cfrac{2}{2}\)，\(DF\)\(=\)\(\cfrac{6}{2}\)，则 \(OF\)\(=\)\(\cfrac{1}{3}DF\)\(=\)\(\cfrac{\sqrt{6}}{6}\)，又由\(Rt\triangle A_1B_1F\) 可得 \(A_1F\)\(=\)\(\cfrac{\sqrt{6}}{2}\)，故 \(\cos\angle A_1FO\)\(=\)\(\cfrac{OF}{A_1F}\)\(=\)\(\cfrac{1}{3}\)；

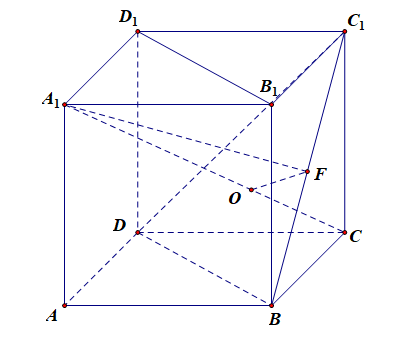
其二，从数上思考，由上述可知所求的线面角为 \(\angle A_1FO\)，在 \(Rt\triangle A_1FO\) 中，由于 \(A_1O\) 的长度为定值，故可设 \(A_1O\)\(=\)\(a\)，\(OF\)\(=\)\(x\)，则 \(A_1F\)\(=\)\(\sqrt{x^2+a^2}\)，这样 \(\cos\angle\)\(A_1FO\)\(=\)\(\cfrac{OF}{A_1F}\)\(=\)\(\cfrac{x}{\sqrt{x^2+a^2}}\)\(=\)\(\sqrt{\cfrac{x^2}{x^2+a^2}}\)\(=\)\(\sqrt{\cfrac{x^2+a^2-a^2}{x^2+a^2}}\)\(=\)\(\sqrt{1-\cfrac{a^2}{x^2+a^2}}\).

由于 \(a\) 为常数，故当 \(x>0\) 时，\(x\nearrow\)，\(x^2\nearrow\)，\(x^2+a^2\nearrow\)，\(\cfrac{a^2}{x^2+a^2}\searrow\)，\(-\cfrac{a^2}{x^2+a^2}\nearrow\)，\(1-\cfrac{a^2}{x^2+a^2}\nearrow\)，\(\sqrt{1-\cfrac{a^2}{x^2+a^2}}\nearrow\)，故当 \(x\nearrow\)，\(\cos\angle\)\(A_1FO\nearrow\)，又由于 \(y=\cos x\) 为 \([0,\cfrac{\pi}{2}]\) 上的减函数，故如果要 \(\angle\)\(A_1FO\) 最大，则需要 \(\cos\angle\)\(A_1FO\) 最小，即需要 \(x\) 最小，这样就需要 \(OF\) 最小，而直线外一点和直线上的动点之间的点点距中只有垂线段最短，故需要 \(OF\perp BC_1\)， 依托思路一求得 \(A_1O=\cfrac{2\sqrt{3}}{3}\)，\(OF\)\(=\)\(\cfrac{\sqrt{6}}{6}\)，代入求得 \(\cos\angle A_1FO\)\(=\)\(\cfrac{OF}{A_1F}\)\(=\)\(\cfrac{1}{3}\)；

面面角

【2017凤翔中学第三次月考理科第19题】如图所示，四棱锥 \(P-ABCD\) 中，底面 \(ABCD\) 是个边长为 \(2\) 的正方形，侧棱 \(PA\perp\) 底面\(ABCD\)，且 \(PA=2\) ，\(Q\) 是 \(PA\) 的中点。

(1).证明：\(BD\perp\) 平面 \(PAC\)；

证明：由于侧棱 \(PA\perp\) 底面\(ABCD\)，\(BD\subsetneqq\) 底面 \(ABCD\)，故 \(PA\perp BD\)；

又由于 \(AC\) 和 \(BD\) 是正方形的对角线，则 \(AC\perp BD\)，

则\(BD\perp AC\)，\(BD\perp PA\)，\(PA\cap AC=A\)，

\(PA\subsetneqq\) 平面 \(PAC\)，\(AC\subsetneqq\) 平面 \(PAC\)，

故 \(BD\perp\) 平面 \(PAC\)；

(2).求二面角 \(C-BD-Q\) 的余弦值。【此题目包含平面的法向量的详细求解方法】

✍️思路一，空间向量法，由题可知，\(AB\)、\(AP\)、\(AD\) 两两垂直，以 \(A\) 为坐标原点，分别以 \(AB\)、\(AD\)、\(AP\) 所在直线为 \(x\)，\(y\)，\(z\) 轴建立空间直角坐标系，如图所示。

则点\(B(2，0，0)\)，\(C(2，2，0)\)，\(D(0，2，0)\)，\(Q(0，0，1)\)，

所以 \(\overrightarrow{BD}=(-2，2，0)\)，\(\overrightarrow{BQ}=(-2，0，1)\)，

设平面 \(BDQ\) 的法向量为 \(\vec{m}=(x，y，z)\)，^[2] 则有

$\begin{cases}\vec{m}\perp\overrightarrow{BD}\\\vec{m}\perp\overrightarrow{BQ}\end{cases}$ $\Longrightarrow \begin{cases}\vec{m}\cdot\overrightarrow{BD}=0\\\vec{m}\cdot\overrightarrow{BQ}=0\end{cases}$

即\(\begin{cases}-2x+2y=0\\-2x+z=0\end{cases}\)，可以取 \(\vec{m}=(1，1，2)\) 由于得到的方程组是不定方程组，应该有无穷多组解，此处只关注其存在性，故可以通过赋值来得到这个不定方程组的解。比如考虑到运算的简单，我们令\(x=1\)，则得到\(y=1\)，\(z=2\)，则 \(\vec{m}\)\(=\)\((1,1,2)\)

平面 \(BDC\) 的法向量为 \(\vec{n}=(0，0，1)\)可以用同样的思路和方法来求解法向量，当然也可以用更快捷的方法，比如我们注意到平面 \(BDC\) 也就是平面 \(ABCD\)，故其法向量可以取 \(z\) 轴所在直线的方向向量，为简单起见，取为\((0,0,1)\)，

设二面角 \(C-BD-Q\) 的平面角为 \(\theta\)，由图可知 \(\theta\) 为钝角1、平面角为锐角或钝角是直观观察得到的；2、\(<\vec{m},\vec{n}>\) 可能为锐角，也可能为钝角，故使用 \(|\cos<\vec{m},\vec{n}>|\) 来限制，又由于平面角为钝角，故\(cos\theta\)\(=\)\(-|cos<\vec{m}，\vec{n}>|\)，则有

\[cos\theta=-|cos<\vec{m}，\vec{n}>|=-\cfrac{\vec{m}\cdot\vec{n}}{|\vec{m}||\vec{n}|}=-\cfrac{2}{\sqrt{6}}=-\cfrac{\sqrt{6}}{3} \]

所以二面角 \(C-BD-Q\) 的余弦值为 \(-\cfrac{\sqrt{6}}{3}\) .

延申阅读①:各种角的求解；延申阅读②:二面角的平面角求法；

✍️思路二，定义法，求解步骤为[作---证---算]；令 \(AC\) 与 \(BD\) 的交点为 \(E\)，连结 \(QE\) 和 \(QC\)，则 \(\angle QEC\) 为所求二面角的平面角[一作]，理由如下：

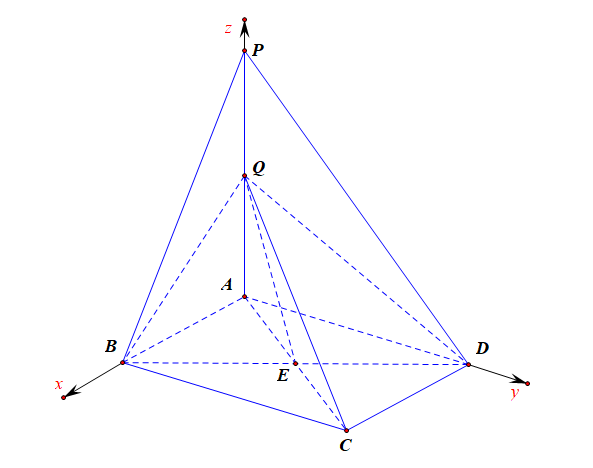
由于底面 \(ABCD\) 是正方形，故 \(EC\perp BD\)，又由于 \(BD\perp AC\)，\(BD\perp AP\)，则 \(BD\perp\) 平面 \(QAC\)，\(QE\subsetneqq\) 平面 \(QAC\)，故 \(BD\perp QE\)，到此满足条件 \(QE\perp BD\)，又 \(EC\perp BD\)，则 \(\angle QEC\) 为所求二面角 \(C-BD-Q\) 的平面角[二证] .

由题目可知， \(ABCD\) 是边长为 \(2\) 的正方形，则 \(AC=2\sqrt{2}\)，\(EC=\sqrt{2}\)，又 \(QA=1\)，则由勾股定理可知 \(QE=\sqrt{3}\)， \(QC=3\)，

到此可知，在 \(\triangle QEC\) 中，\(EC=\sqrt{2}\)，\(QE=\sqrt{3}\)，\(QC=3\)，利用余弦定理可知，

\(\cos\angle QEC\)\(=\)\(\cfrac{EC^2+QE^2-QC^2}{2\times EC\times QE}\)\(=\)\(\cfrac{2+3-9}{2\times\sqrt{2}\times\sqrt{3}}\)\(=\)\(-\cfrac{\sqrt{6}}{3}\)[三算] .

所以二面角 \(C-BD-Q\) 的余弦值为 \(-\cfrac{\sqrt{6}}{3}\) .

[解后反思]：思路二主要使用在高一阶段，学生初次学习了二面角，还没有学习空间向量，这种方法的优越性在于能明白无误的做出来平面角，知道它在图形中的什么地方，也能准确的计算出来，思路一主要使用在学生学习了空间向量之后，这种方法即使你不知道所求的平面角如何作，也能进行相关的计算，不足之处是学生对二面角的平面角在哪里，长什么样子都可能糊里糊涂，所以这几年有高校的老师强烈建议取消思路一的教学，强制使用思路二，也不无道理。

【2019年高考数学试卷理科新课标Ⅱ第17题】如图，长方体\(ABCD-A_1B_1C_1D_1\)的底面\(ABCD\)是正方形，点\(E\)在棱\(AA_1\)上，\(BE\perp EC_1\).

(1).证明：\(BE\perp\)平面\(EB_1C_1\)；

分析：需要证明线面垂直，往往先要转化为证明线线垂直；

解析：由已知\(B_1C_1\perp\)平面\(ABB_1A_1\)，\(BE\subset\)平面\(ABB_1A_1\)，故\(B_1C_1\perp BE\)，

又\(BE\perp EC_1\)，\(B_1C_1\subset\)平面\(EB_1C_1\)，\(EC_1\subset\)平面\(EB_1C_1\)，\(B_1C_1\cap EC_1=C_1\)，

故\(BE\perp\)平面\(EB_1C_1\)；

(2).若\(AE=A_1E\)，求二面角\(B-EC-C_1\)的正弦值；

解析：由(1)知道\(\angle BEB_1=90^{\circ}\)，由题设可知\(Rt\triangle ABE Rt\triangle A_1B_1E\)，所以\(\angle AEB=45^{\circ}\)，故\(AE=AB\)，\(AA_1=2AB\)，

以\(D\)为坐标原点，\(\overrightarrow{DA}\)的方向为\(x\)轴的正方向，\(|\overrightarrow{DA}|\)为单位长，建立如图所示的空间直角坐标系\(D-xyz\)，

则\(C(0，1，0)\)，\(B(1，1，0)\)，\(C_1(0，1，2)\)，\(E(1，0，1)\)，\(\overrightarrow{CB}=(1，0，0)\)，\(\overrightarrow{CE}=(1，-1，1)\)，\(\overrightarrow{CC_1}=(0，0，2)\)，

设平面\(EBC\)的法向量\(\vec{n}=(x，y，z)\)，

则\(\left\{\begin{array}{l}{\overrightarrow{CB}\cdot \vec{n}=0}\\{\overrightarrow{CE}\cdot \vec{n}=0}\end{array}\right.\)，即\(\left\{\begin{array}{l}{x=0}\\{x-y+z=0}\end{array}\right.\)，所以可以赋值取\(\vec{n}=(0，-1，-1)\)，

设平面\(ECC_1\)的法向量\(\vec{m}=(x，y，z)\)，

则\(\left\{\begin{array}{l}{\overrightarrow{CC_1}\cdot \vec{m}=0}\\{\overrightarrow{CE}\cdot \vec{m}=0}\end{array}\right.\)，即\(\left\{\begin{array}{l}{2z=0}\\{x-y+z=0}\end{array}\right.\)，所以可以赋值取\(\vec{m}=(1，1，0)\)，

于是，\(cos<\vec{n}，\vec{m}>=\cfrac{\vec{n}\cdot\vec{m}}{|\vec{n}||\vec{m}|}=-\cfrac{1}{2}\)，

即\(<\vec{n}，\vec{m}>=120^{\circ}\)，所以，二面角\(B-EC-C_1\)的正弦值为\(\cfrac{\sqrt{3}}{2}\)。

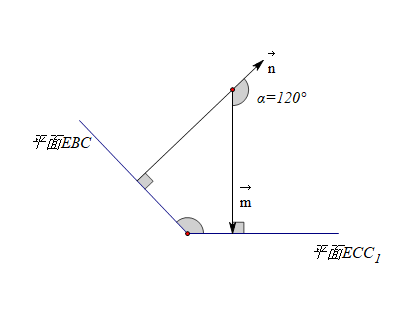
解后反思：

1、当然，本题目同样可用点\(C\)做为坐标原点来建立坐标系。

2、如果我们选取的坐标系不同，很可能\(<\vec{n}，\vec{m}>=60^{\circ}\)，则仿照如图所示，二面角的平面角为\(60^{\circ}\)，则二面角\(B-EC-C_1\)的正弦值还为\(\cfrac{\sqrt{3}}{2}\)。

【2020届宝鸡质检1文数第16题】如图所示，三棱锥\(P-ABC\)中，\(PA\perp\)平面\(ABC\)，\(PA=\)\(AB\)\(=AC\)\(=BC\)\(=2\)，\(E\)是\(PC\)的中点，求异面直线\(AE\)与\(PB\)所成角的余弦值___________。

法1：理科学生可以使用建立空间直角坐标系的思路求解；

法2：平移构造三角形法，取\(BC\)的中点\(F\)，连接\(EF\)和\(AF\)，

则由\(EF//PB\)，可知\(\angle AEF\)即为两条异面直线\(AE\)与\(PB\)所成的角，

在\(\triangle AEF\)中，容易知道\(AE=EF=\sqrt{2}\)，\(AF=\sqrt{3}\)，

由余弦定理可知，\(cos\angle AEF=\cfrac{1}{4}\)；

【2023年高考理科数学乙卷版第19题】如图，在三棱锥 \(P-ABC\)中，\(AB\perp BC\)，\(AB=2\)，\(BC=2\sqrt{2}\)，\(PB=PC=\sqrt{6}\)，\(BP\)、\(AP\)、\(BC\) 的中点分别为 \(D\)、\(E\)、\(O\)， \(AD=\sqrt{5}DO\)， 点 \(F\) 在 \(AC\) 上，\(BF\perp AO\)。

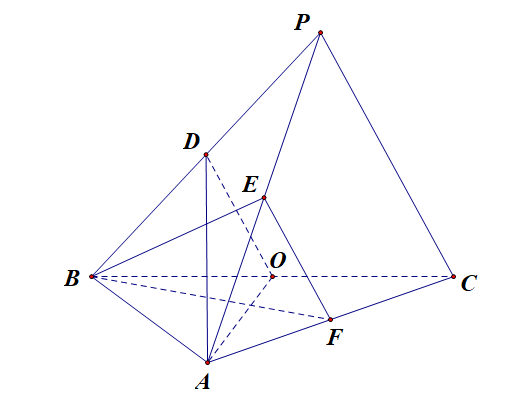
(1). 证明： \(EF//\) 平面 \(ADO\)；

✍️思路一：由于点 \(A\)、\(F\)、\(C\)三点共线，故必然存在唯一的实数 \(t\) ，满足条件 \(\overrightarrow{BF}=(1-t)\cdot\overrightarrow{BA}+t\cdot\overrightarrow{BC}\)，^[3]

又由于 \(BF\perp AO\)，故 \(\overrightarrow{BF}\cdot\overrightarrow{AO}=0\)，即 \(\overrightarrow{BF}\cdot(\overrightarrow{BO}-\overrightarrow{BA})=0\)，

也即 \(\left[(1-t)\cdot\overrightarrow{BA}+t\cdot\overrightarrow{BC}\right]\cdot\left[\cfrac{1}{2}\overrightarrow{BC}-\overrightarrow{BA}\right]=0\)，

由于 \(\angle ABC=90^{\circ}\)，则整理得到，\(-t\cdot\overrightarrow{BA}^2+\cfrac{1-t}{2}\cdot\overrightarrow{BC}^2=0\)，

即 \(-4t+4(1-t)=0\)，解得 \(t=\cfrac{1}{2}\)，

则 \(F\) 为 \(AC\) 的中点^[4]， 由 \(D\)，\(E\)，\(O\)，\(F\) 分别为 \(PB\)、 \(PA\)、 \(BC\)、 \(AC\) 的中点，

于是 \(DE//AB\)， \(DE=\cfrac{1}{2}AB\)， \(OF//AB\)， \(OF=\cfrac{1}{2}AB\)，

即 \(DE//OF\)，\(DE=OF\)， 则四边形 \(ODEF\) 为平行四边形，

\(EF//DO\)， \(EF=DO\)， 又 \(EF\not\subset\) 平面 \(ADO\)， \(DO\subset\) 平面 \(ADO\)，所以 \(EF//\) 平面 \(ADO\).

✍️思路二：注意到题目中有条件 \(BF\perp AO\)，则我们可以利用为 \(\overrightarrow{BF}\cdot\overrightarrow{AO}=0\)，故求解如下，

由勾股定理可知，\(AC=2\sqrt{3}\) 且 \(\cos\angle BAC=\cfrac{\sqrt{3}}{3}\)，设 \(\overrightarrow{AF}=\lambda\overrightarrow{AC}\)，

由于 \(\overrightarrow{AB}\)\(\cdot\)\(\overrightarrow{AC}\)\(=\)\(|\overrightarrow{AB}|\)\(|\overrightarrow{AC}|\)\(\cos\angle\)\(BAC\)\(=\)\(4\)，

则 \(\overrightarrow{BF}\cdot\overrightarrow{AO}\)\(=\)\((\lambda\overrightarrow{AC}-\overrightarrow{AB})\)\((\cfrac{1}{2}\overrightarrow{AB}+\cfrac{1}{2}\overrightarrow{AC})\)

\(=\cfrac{\lambda}{2}|\overrightarrow{AC}|^2-\cfrac{1}{2}|\overrightarrow{AB}|^2+(\cfrac{\lambda}{2}-\cfrac{1}{2})\overrightarrow{AB}\cdot\overrightarrow{AC}=8\lambda-4=0\)，

解得 \(\lambda=\cfrac{1}{2}\)， 则 \(F\) 为 \(AC\) 的中点，由 \(D\)，\(E\)，\(O\)，\(F\) 分别为 \(PB\)、 \(PA\)、 \(BC\)、 \(AC\) 的中点，

于是 \(DE//AB\)， \(DE=\cfrac{1}{2}AB\)， \(OF//AB\)， \(OF=\cfrac{1}{2}AB\)，

即 \(DE//OF\)，\(DE=OF\)， 则四边形 \(ODEF\) 为平行四边形，

\(EF//DO\)， \(EF=DO\)， 又 \(EF\not\subset\) 平面 \(ADO\)，\(DO\subset\) 平面 \(ADO\)，所以 \(EF//\) 平面 \(ADO\).

(2). 证明： 平面 \(ADO\perp\) 平面 \(BEF\)；

证明：由于 \(AO\)\(=\)\(\sqrt{AB^2+OB^2}\)\(=\)\(\sqrt{6}\)\(=\)\(PC\)\(=\)\(2OD\)， \(AD=\sqrt{5}DO\)，

则由 \(AD^2=AO^2+OD^2\)^[5]，故 \(AO\perp OD\)，则有 \(AO\perp EF\)，

由 \(AO\perp BF\)，\(BF\cap EF=F\)，\(BF,EF\subset\) 平面 \(BEF\)，

则 \(AO\perp\) 平面 \(BEF\)，又由于 \(AO\subset\) 平面 \(ADO\)，

故 平面 \(ADO\perp\) 平面 \(BEF\)；

(3). 求二面角 \(D-AO-C\) 的正弦值；

解：设二面角 \(D-AO-C\) 的平面角为 \(\theta\)，则由 \(AO\perp OD\)， \(AO\perp BF\)，则 \(\theta\) 为 \(\overrightarrow{OD}\) 与 \(\overrightarrow{BF}\) 的夹角，

又由于 \(|\overrightarrow{BF}|=\cfrac{1}{2}|\overrightarrow{BF}|=\sqrt{3}\)， \(|\overrightarrow{OD}|=\cfrac{1}{2}|\overrightarrow{PC}|=\cfrac{\sqrt{6}}{2}\)，\(\cos\angle PCD=\cos\angle DOB=\cfrac{\sqrt{2}}{\sqrt{6}}=\cfrac{\sqrt{3}}{3}\)，

则 \(\cos\theta=\cfrac{\overrightarrow{BF}\cdot\overrightarrow{OD}}{|\overrightarrow{BF}||\overrightarrow{OD}|}=\cfrac{\cfrac{1}{2}(\overrightarrow{OA}-3\overrightarrow{OB})\cdot\overrightarrow{OD}}{|\overrightarrow{BF}||\overrightarrow{OD}|}=\cfrac{-\cfrac{3}{2}\overrightarrow{OB}\cdot\overrightarrow{OD}}{|\overrightarrow{BF}||\overrightarrow{OD}|}\)

\(=\cfrac{-\cfrac{3}{2}\times\sqrt{2}\times\cfrac{\sqrt{6}}{2}\times\cfrac{\sqrt{3}}{3}}{\sqrt{3}\times\cfrac{\sqrt{6}}{2}}=-\cfrac{\sqrt{2}}{2}\)，即此平面角为钝角，

则 \(\sin\theta=\cfrac{\sqrt{2}}{2}\)，即二面角 \(D-AO-C\) 的正弦值为 \(\cfrac{\sqrt{2}}{2}\)，

---

1. 比如，积累正方体中体对角线 \(A_1C\perp\) 平面 \(BC_1D\)，且知道 \(A_1O=\cfrac{2}{3}A_1C\)，等等，数学学习中的好多东西是需要积累的； ↩︎

2. 如果一条直线和平面内的两条相交直线都垂直，则该直线和平面垂直。 ↩︎

3. 我们拿到这个题目，一般都会想到转化为通过证明线线平行来证明线面平行，但就是这个线线平行是此题目中的难点，你看着线线是平行的，但常规思路就是不能证明这一点；此题目此处主动应用三点共线的向量表示形式，非常巧妙，引入参数 \(t\)，目的是为了下一步求解 \(t=\cfrac{1}{2}\)，从而得到点 \(F\) 是 \(AC\) 的中点，这样就方便下一步说明线线平行； ↩︎

4. 当 \(t=\cfrac{1}{2}\) 时，由 \(\overrightarrow{BF}\)\(=\)\(\cfrac{1}{2}\overrightarrow{BA}\)\(+\)\(\cfrac{1}{2}\overrightarrow{BC}\)，由向量加法的平行四边形法则可以推导得到 \(F\) 为 \(AC\) 的中点 . ↩︎

5. 由数量的关系得到形式上的关系，也是非常常用的思路之一； ↩︎