平行垂直的证明思路分析

前言

从对象上说，涉及线线位置关系，线面位置关系，面面位置关系；从位置上说，无非研究两种最特殊的情况：平行和垂直，故而有了以下几种情况：

✍️ 线面平行

【2016江苏高考卷】如图，在直三棱柱\(ABC-A_1B_1C_1\)中，\(D\)、\(E\)分别是\(AB\)、\(BC\)的中点，点\(F\)在侧棱\(BB_1\)上，且\(B_1D\perp A_1F\)，\(A_1C_1\perp A_1B_1\)。

求证：(1)直线\(DE//\)平面\(A_1C_1F\).

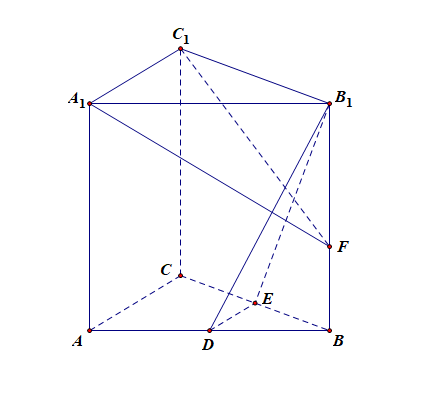
本题目如何分析呢？

分析：分析过程涉及逆向思维，由线面平行的判定定理如果平面外一条直线和平面内的一条直线平行，那么这条直线就和该平面平行。可知，现在需要得到：

\[\Leftarrow 直线 DE//平面 A_1C_1F\Leftarrow\left\{\begin{array}{l}{直线 DE//直线 m}\\{m\subset 平面 A_1C_1F，难点}\\{直线 DE\not\subset 平面 A_1C_1F}\end{array}\right. \]

难点突破：难点是在平面 \(A_1C_1F\) 中寻找这条待定的神秘的直线 \(m\) ，寻找来源：她有可能是三角形平面[或其他的多边形平面，三角形的更多见]的边界线，三角形中线，高线，中位线[低阶层次]，或者需要我们做出的某条辅助直线[中阶层次，涉及到数学知识的主动应用意识]。

证明：因为\(D\)、\(E\)分别是\(AB\)、\(BC\)的中点，

则有 \(DE//AC//A_1C_1\)， 故由

\[\left.\begin{array}{l}{DE//A_1C_1}\\{直线 A_1C_1\subset 平面 A_1C_1F}\\{DE\not\subset 平面 A_1C_1F }\end{array}\right\}\Rightarrow 直线DE//平面A_1C_1F \]

备注：关于线面位置的表示符号，已经变换过多次，转换为你所对应使用的版本即可；另外，这种书写形式的逻辑关系非常清晰，建议使用。倒过来就是分析，顺过去就是证明过程。

✍️ 面面垂直

【2016江苏高考卷】如图，在直三棱柱\(ABC-A_1B_1C_1\)中，\(D\)、\(E\)分别是\(AB\)、\(BC\)的中点，点\(F\)在侧棱\(BB_1\)上，且\(B_1D\perp A_1F\)，\(A_1C_1\perp A_1B_1\)。

求证：(2) 平面 \(B_1DE\perp\) 平面 \(A_1C_1F\).

分析：分析过程涉及逆向思维，由面面垂直的判定定理如果一个平面过另一个平面的垂线，那么这两个平面垂直．可知，现在需要得到：

\[\Leftarrow 平面 B_1DE\perp平面 A_1C_1F\Leftarrow[二选一即可]\left\{\begin{array}{l}{可选途径1：寻找某直线 m\subset 平面B_1DE，证明直线 m\perp平面 A_1C_1F}\\{可选途径2：寻找某直线 n\subset 平面A_1C_1F，证明直线 n\perp平面 B_1DE}\end{array}\right. \]

难点突破：以可选途径1为例说明，难点是在平面 \(B_1DE\) 中寻找的这条待定的神秘直线 \(m\) 要能容易证明直线 \(m\)\(\perp\) 平面 \(A_1C_1F\)，寻找来源：直线 \(m\) 有可能是三角形平面[或其他的多边形平面，三角形的更多见]的边界线，三角形中线，高线，中位线[低阶层次]，或者需要我们做出的某条辅助直线[中阶层次，涉及到数学知识的主动应用意识]。此时往往需要结合图形及已知条件来确定 .

本题目按照思路一该如何分析呢？

【思路一】：当思路转化为证明线面垂直后，结合题目给定的 \(A_1F\perp B_1D\)，不妨选定可选途径2，来分析探索

\(\Leftarrow 直线 A_1F\perp平面 B_1DE\)

\(\Leftarrow\left\{\begin{array}{l}{A_1F\perp B_1D，题目已知}\\{A_1F\perp DE，需要证明，主次转换，转证 DE\perp A_1F}\\{B_1D\subset 平面B_1DE}\\{DE\subset 平面B_1DE}\\{B_1D\cap DE=D}\end{array}\right.\)

\(\Leftarrow\) 接上，重点推求 \(DE\perp A_1F\) \(\Leftarrow\left\{\begin{array}{l}{A_1F\subset 平面 ABB_1A_1}\\{DE\perp 平面 ABB_1A_1，又 DE//AC//A_1C_1}\end{array}\right.\)

\(\Leftarrow\)\(A_1C_1\perp\) 平面 \(ABB_1A_1\) \(\Leftarrow\left\{\begin{array}{l}{A_1C_1\perp A_1B_1，已知}\\{A_1C_1\perp A_1A，由直三棱柱可知}\\{A_1A\subset 平面ABB_1A_1}\\{A_1B_1\subset 平面ABB_1A_1}\\{A_1B_1\cap A_1B=A_1}\end{array}\right.\)

分析到此，水到渠成，将上述的推理逆推即可写出证明过程。

证明：结合题目的已知条件，可得

\(\left.\begin{array}{l}{A_1C_1\perp A_1B_1，已知}\\{A_1C_1\perp A_1A，由直三棱柱可知}\\{A_1A\subset 平面ABB_1A_1}\\{A_1B_1\subset 平面ABB_1A_1}\\{A_1B_1\cap A_1B=A_1}\end{array}\right\}\Rightarrow A_1C_1\perp 平面 ABB_1A_1\)

又由于 \(DE//A_1C_1\)，则 \(DE\perp\) 平面 \(ABB_1A_1\)，

又由于 \(A_1F\subset\) 平面 \(ABB_1A_1\)，故 \(DE\perp A_1F\)，即 \(A_1F\perp DE\)，

\(\left.\begin{array}{l}{A_1F\perp B_1D，已知}\\{A_1F\perp DE，已证}\\{B_1D\subset 平面B_1DE}\\{DE\subset 平面B_1DE}\\{B_1D\cap DE=D}\end{array}\right\}\Rightarrow 直线 A_1F\perp平面 B_1DE\)，

又由于 \(A_1F\subset\) 平面 \(A_1C_1F\)，故 平面 \(B_1DE\perp\) 平面 \(A_1C_1F\).

本题目按照思路二该如何分析呢？

【思路二】：当思路转化为证明线面垂直后，结合题目给定的 \(B_1D\perp A_1F\)，不妨选定可选途径1，来分析探索

\(\Leftarrow 直线 B_1D\perp平面 A_1C_1F\)

\(\Leftarrow\left\{\begin{array}{l}{B_1D\perp A_1F ，题目已知}\\{B_1D\perp A_1C_1，需要证明，主次转换，转证 A_1C_1\perp B_1D}\\{A_1C_1\subset 平面A_1C_1F}\\{A_1F\subset 平面A_1C_1F}\\{A_1C_1\cap A_1F=A_1}\end{array}\right.\)

\(\Leftarrow\) 接上，重点推求 \(A_1C_1\perp B_1D\) \(\Leftarrow\left\{\begin{array}{l}{B_1D\subset 平面 ABB_1A_1}\\{A_1C_1\perp 平面 ABB_1A_1}\end{array}\right.\)

\(\Leftarrow\)\(A_1C_1\perp\) 平面 \(ABB_1A_1\) \(\Leftarrow\left\{\begin{array}{l}{A_1C_1\perp A_1B_1，已知}\\{A_1C_1\perp A_1A，由直三棱柱可知}\\{A_1A\subset 平面ABB_1A_1}\\{A_1B_1\subset 平面ABB_1A_1}\\{A_1B_1\cap A_1B=A_1}\end{array}\right.\)

分析到此，水到渠成，将上述的推理逆推即可写出证明过程。

证明：结合题目的已知条件，可得

\(\left.\begin{array}{l}{A_1C_1\perp A_1B_1，已知}\\{A_1C_1\perp A_1A，由直三棱柱可知}\\{A_1A\subset 平面ABB_1A_1}\\{A_1B_1\subset 平面ABB_1A_1}\\{A_1B_1\cap A_1B=A_1}\end{array}\right\}\Rightarrow A_1C_1\perp 平面 ABB_1A_1\)

又由于 \(B_1D\subset\) 平面 \(ABB_1A_1\)，故 \(A_1C_1\perp B_1D\)，即 \(B_1D\perp A_1C_1\)，

\(\left.\begin{array}{l}{B_1D\perp A_1F，已知}\\{B_1D\perp A_1C_1，已证}\\{A_1F\subset 平面A_1C_1F}\\{A_1C_1\subset 平面A_1C_1F}\\{A_1F\cap A_1C_1=A_1}\end{array}\right\}\Rightarrow 直线 B_1D\perp平面 A_1C_1F\)，

又由于 \(B_1D\subset\) 平面 \(B_1DE\)，故 平面 \(B_1DE\perp\) 平面 \(A_1C_1F\).

【反思提升】上述解答中的思路一中，在分析需要证明\(A_1F\perp DE\)时，包含了视角上的转换，如证明\(A_1F\perp DE\)不容易时，我们转而证明\(DE\perp A_1F\)，即转证\(A_1C_1\perp A_1F\)，从而接下来就可以考虑证明线面垂直，从而转证\(A_1C_1\perp\)包含\(A_1F\)的平面\(ABB_1A_1\)，

✍️ 面面平行

【2019人教A版 \(P_{139}\) 练习 2改编】如图，在正方体 \(ABCD-A_1B_1C_1D_1\) 中，\(M\) 为 \(DD_1\) 的中点，

(1). 求证： \(BD_1//\) 平面 \(AMC\)；

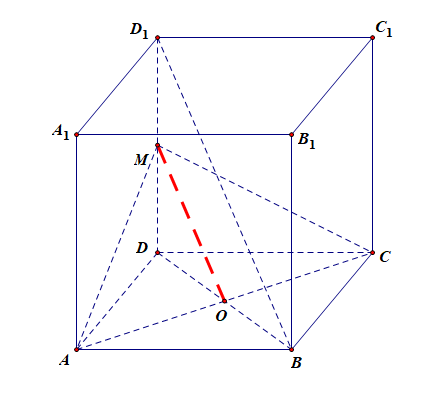
证明：不做分析，直接证明 . 连结 \(BD\) 交 \(AC\) 于点 \(O\) ，因为\(M\)、\(O\)分别是\(DD_1\)、\(BD\)的中点，

则有 \(OM//BD_1\)， 故由

\[\left.\begin{array}{l}{OM//BD_1}\\{直线 OM\subset 平面 AMC}\\{BD_1\not\subset 平面 AMC }\end{array}\right\}\Rightarrow 直线BD_1//平面AMC \]

(2). 在线段 \(CC_1\) 上是否存在一点 \(N\)，使得平面 \(AMC//\) 平面 \(BND_1\)，说明理由 .

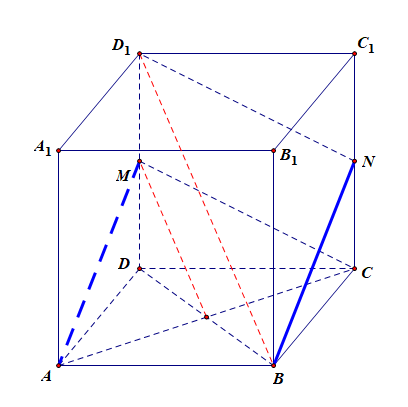
本题目如何分析呢？

分析：本题目探求是否存在条件使得两个平面平行，由两个平面相互平行的判定定理如果一个平面内的两条相交直线与另一个平面平行，那么这两个平面平行．可知，我们需要知道两个某一个平面内的两条相交直线都分别平行于另一个平面，而由 (1) 可知，已经有了 \(BD_1//\) 平面 \(AMC\)，即相当于我们已经有了平面 \(BND_1\) 里面的一条直线 \(BD_1\) 了，现在如果在平面 \(BND_1\) 内再有另一条和直线 \(BD_1\) 相交的直线，也能和平面 \(AMC\) 平行，那么就说明平面 \(AMC//\) 平面 \(BND_1\)，观察点 \(N\) 的位置，如果它的位置能使得 \(BN//AM\)，则能推出线面平行，又点 \(M\) 为 \(DD_1\) 的中点，故可以确定令 \(N\) 为 \(CC_1\) 的中点即可满足条件。

证明：存在点 \(N\) 为 \(CC_1\) 的中点，使得平面 \(AMC//\) 平面 \(BND_1\)，理由如下：

由于 \(M\)、\(N\)分别是\(DD_1\)、\(CC_1\)的中点，

则有 \(AM//BN\)， 故由

\(\left.\begin{array}{l}{AM//BN}\\{直线 AM\subset 平面 AMC}\\{BN\not\subset 平面 AMC }\end{array}\right\}\Rightarrow 直线BN//平面AMC\)

\(\left.\begin{array}{l}{BD_1//平面 AMC，(1)}\\{BN//平面 AMC，已证}\\{BD_1\subset 平面BND_1}\\{BN\subset 平面BND_1}\\{BD_1\cap BN=B}\end{array}\right\}\Rightarrow 平面 BND\perp平面 AMC\) .

✍️ 线面垂直

【常用必记结论】如图所示的是正方体 \(ABCD-A'B'C'D'\)，证明：\(B'D\perp\) 平面 \(ACD'\)

本题目如何分析呢？

分析：分析过程涉及逆向思维，由线面垂直的判定定理如果一条直线与平面内两条相交直线都垂直，那么这条直线与这个平面垂直可知，现在需要得到：

\[\Leftarrow 直线 B'D\perp平面 ACD'\Leftarrow\left\{\begin{array}{l}{B'D\perp m}\\{m\subset 平面 ACD'}\\{B'D\perp n}\\{n\subset 平面 ACD'}\\{m\cap n=?}\end{array}\right. \]

难点突破：难点是在平面 \(ACD'\) 中寻找的这两条待定的神秘直线 \(m\) 和 \(n\)，寻找来源：直线 \(m\) 和 \(n\) 有可能是三角形平面[或其他的多边形平面，三角形的更多见]的边界线，三角形中线，高线，中位线[低阶层次]，或者需要我们做出的某条辅助直线[中阶层次，涉及到数学知识的主动应用意识]。此时往往需要结合图形及已知条件来确定 .

到此，问题转换为证明线线垂直，比如我们选直线 \(AC\) 和 \(AD'\)，来证明 \(B'D\perp AC\) 和 \(B'D\perp AD'\) ，由于 \(BD'\) 为正方体的体对角线，而 \(AC\) 和 \(AD'\) 都是面对角线，两个处于同等的并列位置，故只要突破 \(B'D\perp AC\) ，剩余的 \(B'D\perp AD'\) ，和刚才的证明应该是同理的。而当 \(B'D\perp AC\) 不能突破时，需要转换视角，变换为证明 \(AC\perp B'D\)，

\[\Leftarrow 直线 AC\perp B'D\Leftarrow\left\{\begin{array}{l}{AC\perp 平面 BB'D\Rightarrow 线面垂直}\\{B'D\subset 平面 BB'D}\end{array}\right. \]

\[\Leftarrow 直线 AC\perp平面 BB'D\Leftarrow\left\{\begin{array}{l}{AC\perp m[BD]}\\{m[BD]\subset 平面 BB'D}\\{AC\perp n[BB']}\\{n[BB']\subset 平面 BB'D}\\{m[BD]\cap n[BB']=B}\end{array}\right. \]

证明：有待格式的编辑完善。

令体对角线\(B'D\)和平面\(ACD'\)的交点是\(N\)，由正四面体\(B'-ACD'\)可知，

\(N\)是三角形底面的中心，连接\(OD'\)，则易知\(AC\perp BD\)，\(AC\perp BB'\)，故\(AC\perp B'D\)，

同理\(AD'\perp B'D\)，故体对角线\(B'D\perp\)平面\(ACD'\)。

证法2：空间向量法，

\(\overrightarrow{AC}\cdot\overrightarrow{B'D}=(\overrightarrow{AB}+\overrightarrow{BC})\cdot(\overrightarrow{B'B}+\overrightarrow{BD})\)

\(=\overrightarrow{AB}\cdot\overrightarrow{B'B}+\overrightarrow{AB}\cdot\overrightarrow{BD}+\overrightarrow{BC}\cdot\overrightarrow{B'B}+\overrightarrow{BC}\cdot\overrightarrow{BD}\)

\(=0+1\times\sqrt{2}\times(-\cfrac{\sqrt{2}}{2})+0+1\times\sqrt{2}\times\cfrac{\sqrt{2}}{2}=0\)，

即 \(\overrightarrow{AC}\perp\overrightarrow{B'D}\)，即 \(B'D\perp AC\)；

同理可得，\(B\;'D\perp AD\;'\)，又由于 $AC\subsetneqq $平面 \(ACD\;'\)，$AD'\subsetneqq $平面 \(ACD\;'\)，\(AD\;'\cap AC=\{A\}\)，

则 \(B\;'D\perp\)平面\(ACD\;'\)

【人教 2019A 版教材\(P_{152}\) 页练习第2题】【阳马】如图所示，四棱锥 \(S-ABCD\) 的底面是正方形，\(SD\perp\) 平面 \(ABCD\)，求证：\(AC\perp\) 平面 \(SDB\) .

本题目采用逆向思维该如何分析呢？

分析：采用逆向思维的逆推方式来探求分析证明思路，由线面垂直的判定定理如果一条直线与一个平面内的两条相交直线垂直，那么该直线与此平面垂直。可知，需要找平面 \(SDB\) 中的两条相交直线，然后证明它们和直线 \(AC\) 垂直即可。

\(\Leftarrow AC\perp 平面 SDB \Leftarrow\left\{\begin{array}{l}{AC\perp BD\Leftarrow 正方形对角线互相垂直}\\{AC\perp SD\Leftarrow SD\perp AC\Leftarrow\left\{\begin{array}{l}{SD\perp 平面 ABCD}\\{AC\subset 平面 ABCD}\end{array}\right.}\\{BD\subset 平面 SDB}\\{SD\subset 平面 SDB}\\{BD\cap SD=D}\end{array}\right.\)

证明： 结合上述分析，逆向书写即可。