正三棱锥
前言
正三棱锥是底面是正三角形,三个侧面是全等的等腰三角形的三棱锥。正三棱锥不等同于正四面体,正四面体必须每个面都是全等的等边三角形。所以正四面体是特殊的正三棱锥。以下为我们解题时常用的几种正三棱锥的配图,要熟练掌握。
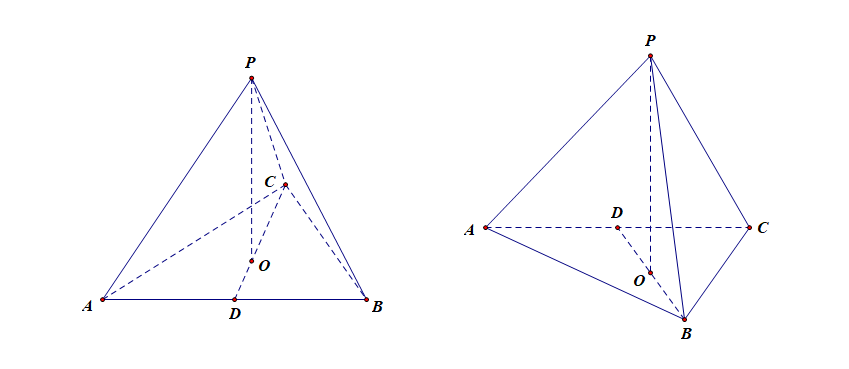
也就是我们解题时需要手工配图的样式图。
相关性质
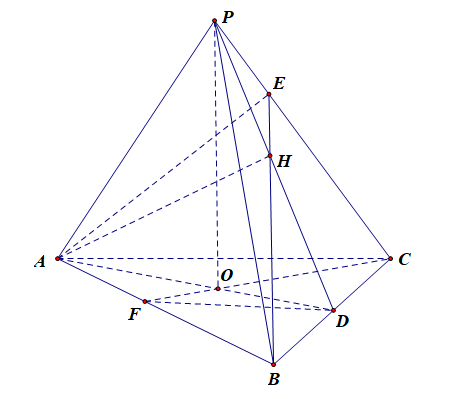
以下图为例,解释说明相关的性质,希望一次过手,一次记准。
1.底面 \(ABC\) 是等边三角形。
2.侧面 \(PAB\)、 \(PBC\)、 \(PAC\) 是三个全等的等腰三角形。
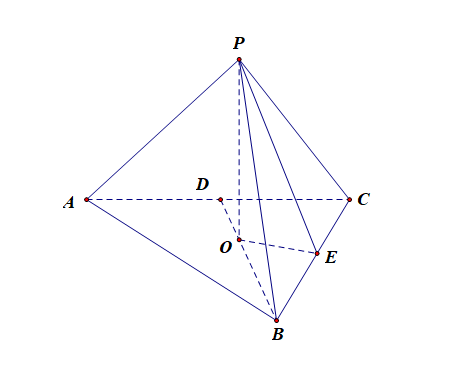
3.顶点 \(P\) 在底面 \(ABC\) 的射影 \(O\) 是底面三角形\(\triangle ABC\) 的中心[也是重心、垂心、外心、内心]。
4.为方便解题,我们常在正三棱锥 \(P-ABC\) 中构造以下四个直角三角形:
①. 斜高 \(PE\) 、侧棱 \(PB\) 、底边的一半 \(BE\) 构成的直角三角形 \(Rt\triangle PEB\) ;
②. 高 \(PO\) 、斜高 \(PE\) 、斜高的射影 \(EO\) 构成的直角三角形 \(Rt\triangle POE\) ;
③. 高 \(PO\) 、侧棱 \(PB\) 、侧棱的射影 \(OB\) 构成的直角三角形 \(Rt\triangle POB\) ;
④. 斜高射影 \(EO\) 、侧棱射影 \(OB\) 、底边的一半 \(BE\) 构成的直角三角形 \(Rt\triangle BOE\) 。
说明:上述直角三角形集中了正三棱锥几乎所有元素。在正三棱锥计算题中,常常取上述直角三角形。这样做的优越性在于不仅使空间问题平面化,而且使平面问题三角化,还使已知元素与未知元素集中于一个直角三角形中,利于解出。
球体与正四面体
-
正四面体的棱长为\(a\),则其高为\(h=\cfrac{\sqrt{6}}{3}a\);
-
正四面体的内切球球心、棱切球球心、外接球球心是同一个点,在正四面体的高上,是高线上接近底面的四等分点。

- 正四面体的内切球半径\(R_{内}=\cfrac{\sqrt{6}a}{12}=\cfrac{1}{4}h=IF\);
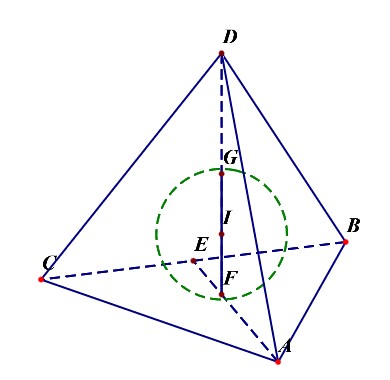
- 正四面体与各棱相切的棱切球的半径\(R_{棱}=\cfrac{\sqrt{2}a}{4}=IE\);
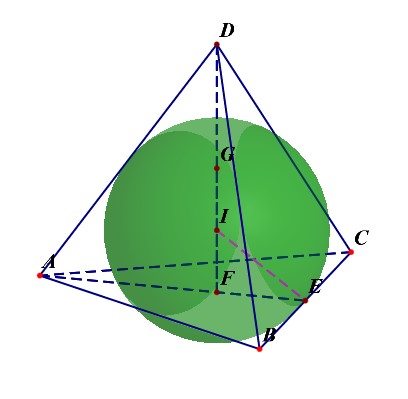
- 正四面体的外接球半径\(R_{外}=\cfrac{\sqrt{6}a}{4}=IC\);
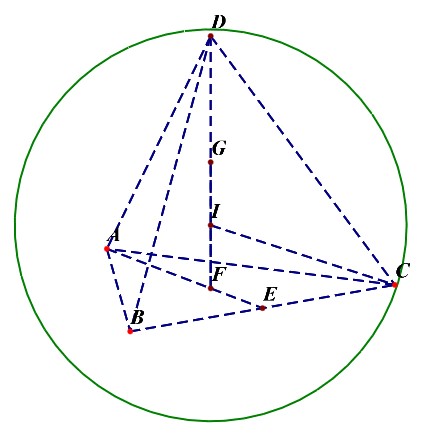
- 正四面体的内切球半径与外接球半径之比为\(R_{内}:R_{外}=1:3\);\(R_{内}=\cfrac{1}{4}h\);\(R_{外}=\cfrac{3}{4}h\);\(h=\cfrac{\sqrt{6}}{3}a\);
球体与正三棱锥
-
正三棱锥的棱长为\(a\);则其高为\(h=\);
-
正三棱锥的内切球半径;
-
正三棱锥的外接球半径;
球体与四面体
- 任意四面体都有内切球和外接球 [1],任意四面体的外接球的球心:过任意两个侧面三角形的外接圆的圆心作垂线,两条垂线的交点即为外接球的球心;
法1:直接找球心,任意四面体的外接球的球心:过任意两个侧面三角形的外接圆的圆心作垂线,两条垂线的交点即为外接球的球心;在此题目中,下底面 \(Rt\triangle BAC\) 的外接圆的圆心为 \(BC\) 的中点,过此点做下底面 \(ABC\) 的垂线,由于平面 \(ABC\perp\) 平面 \(PBC\) ,故所作的垂线和 \(PB\) 相交于点 \(O\),又由于侧面三角形 \(Rt\triangle PBA\),故其外接圆的圆心也在点 \(O\) 处,故点 \(O\) 是三棱锥 \(P-ABC\) 外接球的球心 .
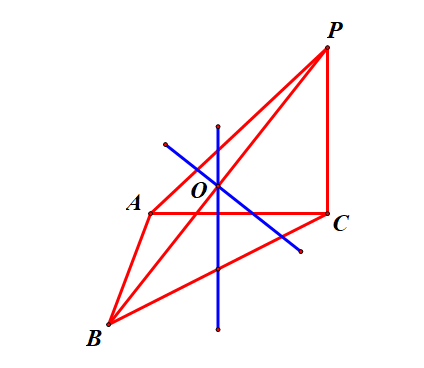
接下来计算,由于 \(\angle BAC=90^{\circ}\),\(AB=3\),\(AC=4\),故 \(BC=5\),又由于 \(PC\perp\) 底面 \(ABC\),\(\angle PCB=90^{\circ}\),\(\angle PBC=60^{\circ}\),则 \(PB=10\),从而 \(R=\cfrac{PB}{2}=5\),则三棱锥 \(P-ABC\) 外接球的体积为 \(V_{P-ABC}=\cfrac{4}{3}\pi R^3=\cfrac{500\pi}{3}\),故选 \(B\) .
法2:补体为长方体;由于注意到题目中有好几个直角,如 \(\angle BAC\)、\(\angle BAC\)、\(\angle PCA\)、\(\angle PCB\),所以能联系到补体为长方体;
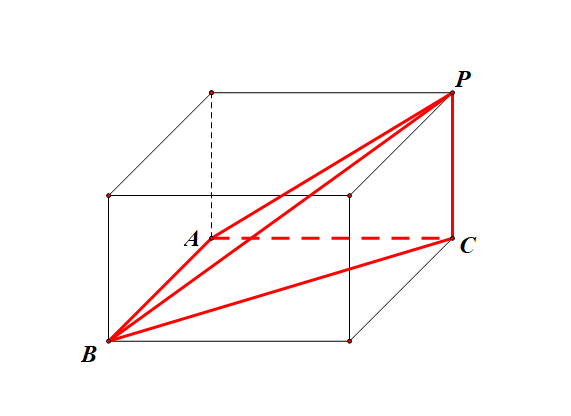
三棱锥 \(P-ABC\) 的外接球和长方体的外接球是相同的,而长方体的外接球的球心为体对角线的中点,由于 \(\angle BAC=90^{\circ}\),\(AB=3\),\(AC=4\),故 \(BC=5\),又由于 \(PC\perp\) 底面 \(ABC\),\(\angle PCB=90^{\circ}\),\(\angle PBC=60^{\circ}\),则 \(PB=10\),从而 \(R=\cfrac{PB}{2}=5\),则三棱锥 \(P-ABC\) 外接球的体积为 \(V_{P-ABC}=\cfrac{4}{3}\pi R^3=\cfrac{500\pi}{3}\),故选 \(B\) .
典例剖析
①\(BC\perp AD\);
②二面角 \(P-AB-C\) 的平面角为 \(\angle PBC\);
③直线 \(PA\) 与平面 \(ABC\) 所成角的大小为 \(\cfrac{\pi}{3}\);
④两条异面直线\(AB\)和\(PC\)间的距离为\(\cfrac{3\sqrt{3}}{4}\);
⑤直线 \(FD\) 与直线 \(PC\) 所成角的余弦值为 \(\cfrac{\sqrt{3}}{3}\);
⑥三棱锥 \(P-ABC\) 的体积为 \(\cfrac{3}{4}\);
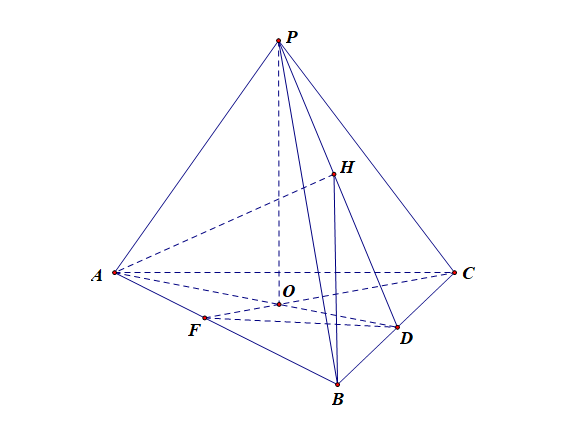
解析:本题目的信息量有点太大,具体解析如下,
①\(BC\perp AD\);
分析:由于点 \(A\) 在侧面 \(PBC\) 上的射影为 \(H\),故\(AH\perp\)平面\(PBC\),由于\(BC\subsetneqq PBC\),故\(AH\perp BC\);
又由于\(H\) 是 \(\triangle PBC\) 的垂心,故\(PD\perp BC\),
由\(BC\perp AH\),\(BC\perp PD\),且又\(AH\),\(PD\subsetneqq\) \(PAD\)、\(AH\cap PD=H\),
则\(BC\perp\)平面\(PAD\),又\(AD\subsetneqq\) \(PAD\),则得到\(BC\perp AD\);故①成立;
②二面角 \(P-AB-C\) 的平面角为 \(\angle PBC\);
分析:如图所示,延长\(BH\)交\(PC\)于点\(E\),连结\(AE\),
则由\(AH\perp PC\),\(BE\perp PC\)(垂足),\(AH\cap BE=H\),\(AH\)、\(BE\subsetneqq\) \(ABE\),
故\(PC\perp\)面\(ABE\),\(AB\subsetneqq\)面\(ABE\),
则有\(PC\perp AB\),又\(PO\perp AB\),\(PC\cap PO=P\),\(PC\)、\(PO\subsetneqq\) \(POC\),
则\(AB\perp POC\),\(CO\subsetneqq\)面\(POC\),
则得到\(AB\perp CO\),则\(AB\perp CF\),
故\(O\)为\(\triangle ABC\)的垂心,又由于三角形为正三角形,
故\(O\)是\(\triangle ABC\)的中心,
故\(P-ABC\)为正三棱锥。
故可知,点\(D\),\(F\)分别为中点,连结\(PF\),则可得到\(PF\perp AB\),
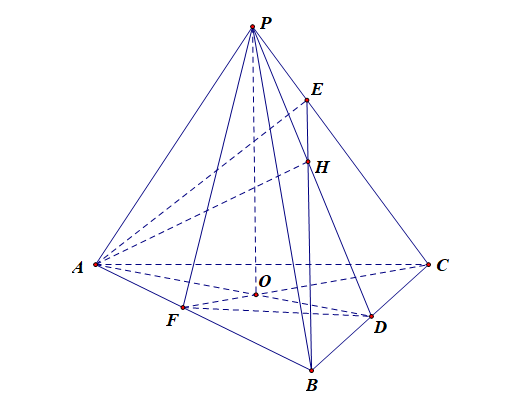
则\(\angle PFC\)为二面角 \(P-AB-C\) 的平面角。故②错误;
③直线 \(PA\) 与平面 \(ABC\) 所成角的大小为 \(\cfrac{\pi}{3}\);
分析:连结\(EF\),由①②可知,\(AB\perp\)平面\(PCF\),故\(AB\perp EF\),又\(PC\perp\)平面\(ABE\),故\(PC\perp EF\),
故线段\(EF\)为两条异面直线\(AB\)和\(PC\)的公垂线,又由于\(CF\perp AB\),
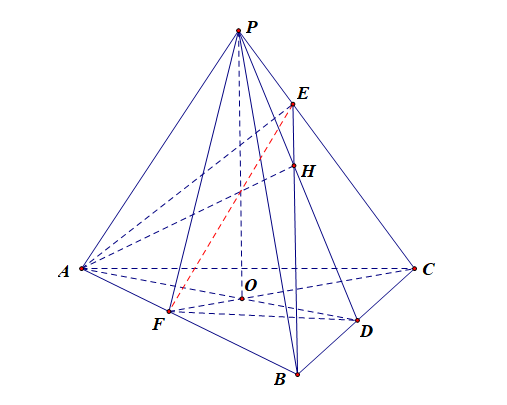
故\(\angle EFC\)为二面角\(H-AB-C\)的平面角,则由已知得\(\angle EFC=\cfrac{\pi}{6}\).
设正三角形\(ABC\)的边长为\(2x\),则\(BD=FB=x\),则\(CF=\sqrt{3}x\),
在\(Rt\triangle CEF\)中,由于\(\angle CFE=\cfrac{\pi}{6}\),故\(CE=\cfrac{\sqrt{3}}{2}x\),\(EF=\cfrac{3}{2}x\);
在\(Rt\triangle CEB\)中,可得\(BE^2=BC^2-CE^2=(2x)^2-(\cfrac{\sqrt{3}}{2}x)^2=\cfrac{13}{4}x^2\),
且由于是正三棱锥,有\(BE=AE\);
又在\(Rt\triangle PAF\)中,则\(PF^2==PA^2-AF^2=2^2-x^2=4-x^2\),
则在\(Rt\triangle PEF\)中,\(PE^2=PF^2-EF^2=4-x^2-\cfrac{9}{4}x^2=4-\cfrac{13x^2}{4}\),
由已知\(PA=2=PC\),即\(PE+CE=PC=2\),即\(\sqrt{4-\cfrac{13x^2}{4}}+\cfrac{\sqrt{3}}{2}x=2\),
移项,得到\(\sqrt{4-\cfrac{13x^2}{4}}=2-\cfrac{\sqrt{3}}{2}x\),两边平方,解得\(x=\cfrac{\sqrt{3}}{2}\),
故可得\(AB=BC=AC=\sqrt{3}\),\(BD=BF=\cfrac{\sqrt{3}}{2}\),\(AD=\cfrac{\sqrt{3}}{2}\times\sqrt{3}=\cfrac{3}{2}\),
则由点\(O\)为正三角形\(ABC\)的重心,得到\(AO=\cfrac{3}{2}\times \cfrac{2}{3}=1\),
在\(Rt\triangle PAO\)中,\(PA=2\),\(AO=1\),故\(\angle PAO=\cfrac{\pi}{3}\).
即直线 \(PA\) 与平面 \(ABC\) 所成角的大小为 \(\cfrac{\pi}{3}\);
④两条异面直线\(AB\)和\(PC\)间的距离为\(\cfrac{3\sqrt{3}}{4}\);
分析:由上可知,线段\(EF\)为两条异面直线\(AB\)和\(PC\)的公垂线,

且\(EF=\cfrac{3}{2}x=\cfrac{3}{2}\times\cfrac{\sqrt{3}}{2}=\cfrac{3\sqrt{3}}{4}\);
即两条异面直线\(AB\)和\(PC\)间的距离为\(\cfrac{3\sqrt{3}}{4}\);故④正确;
⑤直线 \(FD\) 与直线 \(PC\) 所成角的余弦值为 \(\cfrac{\sqrt{3}}{3}\);
分析:由于点\(D\), \(F\)分别是线段\(BC\)和\(AB\)的中点,故\(DF//AC\),
则直线 \(FD\) 与直线 \(PC\) 所成角的也就是直线 \(AC\) 与直线 \(PC\) 所成的角,
由上可知是正三棱锥,故在\(\triangle PAC\)中,\(PA=PC=2\),\(AC=AB=BC=\sqrt{3}\),
故由余弦定理或者构造\(Rt\triangle\)可得到,\(\cos\angle PCA=\cfrac{\sqrt{3}}{4}\),故④错误;
⑥三棱锥 \(P-ABC\) 的体积为 \(\cfrac{3}{4}\);
分析:由上可知,\(PC=2\),\(CD=\cfrac{\sqrt{3}}{2}\),则\(PD^2=PC^2-CD^2=2^2-(\cfrac{\sqrt{3}}{2})^2=\cfrac{13}{4}\),
则\(PO^2=PD^2-OD^2=\cfrac{13}{4}-\cfrac{1}{4}=3\),即\(PO=\sqrt{3}\),
故\(V_{P-ABC}=\cfrac{1}{3}\cdot S_{\triangle ABC}\cdot PO=\cfrac{1}{3}\cdot \cfrac{\sqrt{3}}{4}\cdot(\sqrt{3})^2\cdot \sqrt{3}=\cfrac{3}{4}\),故⑥正确,
综上所述,正确的命题有:①③④⑥;
解后反思:本题目难度很大,从总体求解过程中,我们可以总结出许多有用的结论,
待有空整理;
涉及类比推理:任意三角形都有内切圆,任意四面体都有内切球;任意三角形都有外接圆,任意四面体都有外接球; ↩︎

 正三棱锥与正四面体,正三棱锥的相关性质。
正三棱锥与正四面体,正三棱锥的相关性质。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号