从正三角形到正四面体

三角形的心

三角形的内心：三角形的三个内角平分线的交点，内切圆的圆心

三角形的外心：三角形的三边的中垂线的交点，外接圆的圆心

三角形的重心： 三角形的三边的中线的交点。即平衡点。

三角形的垂心：三角形的三边的高线的交点。

三角形的旁心：三角形的三个外角平分线的交点。【不做研究】

注意三角形的上述几个心的向量表示形式。三角形的四心的向量表示

当三角形由一般的三角形变化为特殊的三角形时，其几个心的位置关系会发生相应的变化。

各种特殊三角形中，如等腰三角形、直角三角形、等腰直角三角形中的情形自行推导。

运算方法

勾股定理，比例关系，等面积法，等体积法。

正三角形的心

正三角形的三线合一：如\(\angle A\)的内角平分线，边\(BC\)的中线，边\(BC\)的高线三线合一。

正三角形的四心合一：由于上述三线合一，故正三角形的内心、外心、重心、垂心四心合一。

正三角形的两圆心合一：正三角形的内切圆圆心、外接圆圆心合二为一。

• 正三角形的内心外心位置：在正三角形的重心位置处，或在正三角形任意一条高线[或中线或垂线]的远离三角形顶点的三等分点处；

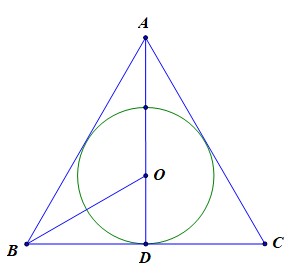
【推导1】思路：如上图所示， \(O\)为\(\Delta ABC\)的内心，也是重心，

设边长\(AB=a\)，则\(BD=\cfrac{a}{2}\)，\(AD=\cfrac{\sqrt{3}a}{2}\)，

\(R{内}=OD=\cfrac{1}{3}\cdot \cfrac{\sqrt{3}a}{2}\)，\(R{外}=OA=\cfrac{2}{3}\cdot \cfrac{\sqrt{3}a}{2}\)，

故\(R_{内}：R_{外}=1：2\)；

【推导2】等面积法：\(S_{\Delta ABC}=S_{\Delta OBC}+S_{\Delta OAC}+S_{\Delta OAB}\)，

即\(\cfrac{1}{2}\times BC\times AD=\cfrac{1}{2}\times BC\times R_{内}+\cfrac{1}{2}\times AC \times R_{内}+\cfrac{1}{2}\times AB\times R_{内}\)，

则\(\cfrac{1}{2}\times BC\times AD=\cfrac{3}{2}\times BC\times R_{内}\)，

故\(R_{内}=\cfrac{1}{3}\cdot AD=\cfrac{1}{3}\cdot h\)，故\(R_{外}=\cfrac{2}{3}\cdot h\)，

故\(R_{内}：R_{外}=1：2\)；

正四面体的心

正四面体的内切球球心、外接球球心、棱切球球心，三心合一。

正四面体的内切球球心、外接球球心、棱切球球心位置：在正四面体任一高线的四等分点处，且靠近底面。

正四面体的棱长为\(a\)，则底面三角形的高为\(\cfrac{\sqrt{3}a}{2}\)，则正四面体的高为\(h=\cfrac{\sqrt{6}a}{3}\)；

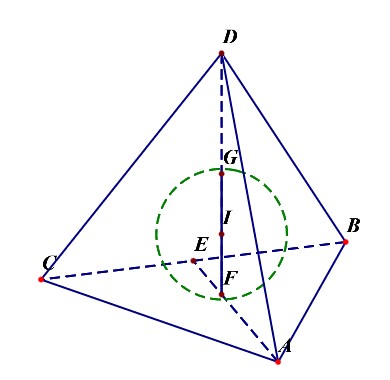
• 正四面体的内切球半径\(R_{内}=\cfrac{\sqrt{6}a}{12}=\cfrac{1}{4}h=IF\)；

推导：等体积法，\(V_{D-ABC}=\cfrac{1}{3}\times S_{\Delta ABC}\times h\)，\(V_{D-ABC}=V_{I-ABC}+V_{I-ABD}+V_{I-BCD}+V_{I-ACD}=\cfrac{4}{3}\times S_{\Delta ABC}\times R_{内}\)，

故\(R_{内}=\cfrac{1}{4}h\)；

• 正四面体的外接球半径\(R_{外}=\cfrac{\sqrt{6}a}{4}=\cfrac{3}{4}h=IC\)；

推导：由上可知，\(R_{外}=\cfrac{3}{4}h\)；

• 正四面体的棱切球半径\(R_{棱}=\cfrac{\sqrt{2}a}{4}=IE\)；

推导：

正四面体性质

正四面体是五种正多面体[正四面体、正六面体、正八面体、正十二面体、正二十面体]中的一种，有 \(4\) 个正三角形的面，\(4\) 个顶点，\(6\) 条棱。正四面体不同于其它四种正多面体，它没有对称中心。正四面体有六个对称面，其中每一个都通过其一条棱和与这条棱相对的棱的中点。正四面体很容易由正方体得到，只要从正方体一个顶点 \(A\) 引三个面的对角线 \(AB\) ，\(AC\) ，\(AD\)，并两点两点连结之即可。

1.正四面体的每一个面是正三角形，反之亦然。

2.正四面体是三组对棱都垂直的等面四面体。

3.正四面体是两组对棱垂直的等面四面体。

4.正四面体的对棱中点的连线都互相垂直且相等，等于棱长的 \(\cfrac{\sqrt{2}}{2}\) 倍，反之亦真。

5.正四面体的各棱的中点是正八面体的六顶点。

6.正四面体的全面积是棱长平方的 \(\sqrt{3}\) 倍，体积是棱长立方的\(\cfrac{\sqrt{2}}{12}\) 倍。

7.正四面体的四个旁切球半径均相等，等于内切球半径的2倍，或等于四面体高线的一半。

8.正四面体的内切球与各侧面的切点是侧面三角形的外心，或内心，或垂心，或重心，除外心外，其逆命题均成立。

9.正四面体的外接球球心到四面体四顶点的距离之和，小于空间中其他任一点到四顶点的距离之和。

10.正四面体内任意一点到各侧面的垂线长的和等于这四面体的高。

11.对于四个相异的平行平面，总存在一个正四面体，其顶点分别在这四个平面上。

12.以正四面体的每条棱为直径作球，设S是所作六个球的交集，则S中含有两点，它们的距离为\(\cfrac{\sqrt{6}}{6}\) 倍棱长。

13.过正四面体的一棱及所对的棱的中点的截面面积与其侧面三角形面积之比为\(\cfrac{\sqrt{6}}{3}\) 。

14.四面体为正四面体的充要条件是，其棱均做为外接平行六面体的侧面对角线时，平行六面体为正方体。

15.四面体为正四面体的充要条件是，其共顶点三棱作为外接平行六面体的棱时，平行六面体为一个三面角均为60°的菱形六面体。

16.四面体为正四面体的充要条件是，四面体在平行于两棱的每一个平面的射影是正方形。

17.四面体为正四面体的充要条件是，四面体的展开图是一个引出了三条中位线的正三角形。

18.正四面体每条高的中点与底面三角形三顶点均构成直角四面体的四顶点，且高的中点为正三面角顶点。

相关阅读：

球体与简单几何体的切接问题

推理与证明