分式函数与高考数学

相关推荐

1、分式之殇

2、分式型函数

3、分式型函数的图像变换源

典例剖析

【2016高考理科全国卷2第12题】已知函数\(f(x)(x\in R)\)满足\(f(-x)=2\) \(-f(x)\)，若函数\(y=\cfrac{x+1}{x}\)与函数\(y=f(x)\)图像的交点为\((x_1，y_1)\)，\((x_2，y_2)\)，\(\cdots\)，\((x_m，y_m)\)，则\(\sum\limits_{i=1}^m{(x_i+y_i)}\)的值为【\(\qquad\)】

$A.0$ $B.m$ $C.2m$ $D.4m$

分析：由题目可知\(f(x)+f(-x)=2\)，即函数\(f(x)\)图像关于点\((0，1)\)对称，

而函数\(y=\cfrac{x+1}{x}=1+\cfrac{1}{x}\)图像也关于点\((0，1)\)对称，即两个函数图像有相同的对称中心，

那么二者的交点个数一定有偶数个，如图所示， 可知对横坐标而言有\(\sum\limits_{i=1}^m{x_i}=0\)，

而对纵坐标而言，成对的点的个数是\(\cfrac{m}{2}\)个，他们中的每一对满足\(\cfrac{y_1+y_m}{2}=1\)，

即\(y_1+y_m=2\)，故\(\sum\limits_{i=1}^m{y_i}=2\cdot \cfrac{m}{2}=m\)，

故\(\sum\limits_{i=1}^m{(x_i+y_i)}=\sum\limits_{i=1}^m{x_i}+\sum\limits_{i=1}^m{y_i}=m\)，故选\(B\)。

【2021年高考乙卷文科数学第\(8\)题】下列函数中最小值为 \(4\) 的函数是【\(\qquad\)】

$A.y=x^2+2x+4$ $B.y=|\sin x|+\cfrac{4}{|\sin x|}$ $C.y=2^x+2^{2-x}$ $D.y=\ln x+\cfrac{4}{\ln x}$

解析：本题目考察函数的最小值或者值域问题，涉及到的函数都很特殊，比如二次函数，对勾型函数，偶函数等；

对于选项 \(A\)，函数特殊却简单，配方即可，\(y=(x+1)^2+3\)，故其是对称轴为 \(x=-1\)，开口向上，最低点为 \((-1,3)\) 的抛物线，最小值为 \(3\)，故不符舍去；

对于选项 \(B\) 和 \(D\) 而言，首先需要清楚对勾函数 \(y=x+\cfrac{4}{x}\) 的图像和性质，

这样，如果我们对 \(y=|\sin x|\) 和 \(y=\ln x\) 的值域非常清楚，则使用换元法就转化成了上述对勾函数的一部分图像问题了，

令 \(t=|\sin x|\) ，则 \(t\in (0,1]\) ，故 选项 \(B\) 中的函数即 \(y=t+\cfrac{4}{t}\)， \(t\in (0,1]\)，函数单调递减，故\(y_{\min}\)\(=\)\(1\)\(+\)\(\cfrac{4}{1}\)\(=\)\(5\)，故排除；其实选项 \(B\) 更多的是想引导你使用均值不等式，这是个坑，原因是正和定两个条件都满足，就是等这个条件无法满足，所以回过头还需要使用对勾函数来求解；

令 \(m=\ln x\) ，则 \(m\in R\) ，在本题目中，\(m\neq 0\) ，故此时 函数 \(y=m+\cfrac{4}{m}\)，是完整的对勾函数，没有最小值，故排除；这个选项不能使用均值不等式，原因是第一条正都不能满足；

对于选项 \(C\) ，我们即可以使用均值不等式，\(y=2^x+2^{2-x}=2^x+\cfrac{4}{2^x}\geqslant 2\sqrt{2^x\times \cfrac{4}{2^x}}=4\)，当且仅当 \(x=1\) 时取得等号，故其最小值为 \(4\) ；也可以利用图像变换得到，首先确定变换的初始函数 \(f(x)=2^x+2^{-x}\)，类似抛物线的开口向上的偶函数，最小值为 \(f(0)=2\)，向右平移一个单位得到\(f(x-1)=2^{x-1}+2^{1-x}\)，最小值还是 \(2\) ，再纵向扩大 \(2\) 倍，得到 \(y=2f(x-1)=2^x+2^{2-x}\)，故最小值变为 \(2\times2=4\) ，故选 \(C\) .

【2021年高考乙卷文科数学第\(9\)题】设函数 \(f(x)=\dfrac{1-x}{1+x}\), 则下列函数中为奇函数的是【\(\qquad\)】

$A.f(x-1)-1$ $B.f(x-1)+1$ $C.f(x+1)-1$ $D.f(x+1)+1$

解析: 本题目的求解涉及到反比例函数，函数的对称性，图像的变换，函数的奇偶性等

由于 \(f(x)=\cfrac{1-x}{1+x}=\cfrac{-(x+1)+2}{1+x}=-1+\cfrac{2}{x+1}\)，

所以函数 \(f(x)\) 的对称中心为 \((-1,-1)\)，

所以将函数 \(f(x)\) 向右平移一个单位，向上平移一个单位，

得到函数 \(y=f(x-1)+1\) ，该函数的对称中心为 \((0,0)\)，

故函数 \(y=f(x-1)+1\) 为奇函数，故选: \(B\) .

【2021年高考乙卷文科数学第 \(19\) 题】 设 \(\{a_{n}\}\) 是首项为 \(1\) 的等比数列，数列 \(\{b_{n}\}\) 满足 \(b_{n}=\cfrac{na_n}{3}\)， 已知 \(a_{1}\)， \(3a_{2}\)， \(9a_{3}\)成等差数列.

(1). 求 \(\{a_{n}\}\) 和 \(\{b_{n}\}\)的通项公式;

解析：由于 \(a_{1}\)， \(3a_{2}\)， \(9a_{3}\)成等差数列， 所以 \(6a_{2}=a_{1}+9a_{3}\)，

又由于 \(\{a_{n}\}\) 是首项为 \(1\) 的等比数列，设其公比为 \(q\)，

则 \(6q=1+9q^{2}\)， 解得， \(q=\cfrac{1}{3}\)，

所以， \(a_{n}=a_{1}\cdot q^{n-1}=(\cfrac{1}{3})^{n-1}\)

则 \(b_{n}=\cfrac{na_n}{3}=n\cdot (\cfrac{1}{3})^{n}\)

(2). 记 \(S_{n}\) 和 \(T_{n}\) 分别为 \(\{a_{n}\}\) 和 \(\{b_{n}\}\) 的前 \(n\) 项和， 证明: \(T_{n}<\cfrac{S_n}{2}\).

解析： 由于 \(a_{n}=(\cfrac{1}{3})^{n-1}\)， \(b_{n}=\cfrac{na_n}{3}=n\cdot (\cfrac{1}{3})^{n}\) ，

则 \(S_{n}=\cfrac{1\times[1-(\cfrac{1}{3})^{n}]}{1-\cfrac{1}{3}}=\cfrac{3}{2}(1-\cfrac{1}{3^n})\)，则 \(\cfrac{S_n}{2}=\cfrac{3}{4}(1-\cfrac{1}{3^n})\)，

由于 \(T_n=b_1+b_2+b_3+\cdots+b_n\)

则 \(T_n=1\cdot\cfrac{1}{3}+2\cdot\cfrac{1}{3^2}+3\cdot\cfrac{1}{3^3}+\cdots+n\cdot\cfrac{1}{3^n}\) \(\quad\quad①\)

\(\cfrac{1}{3}\cdot T_n=\quad\quad 1\cdot\cfrac{1}{3^2}+2\cdot\cfrac{1}{3^3}+\cdots+(n-1)\cdot\cfrac{1}{3^n}+n\cdot\cfrac{1}{3^{n+1}}\) \(\quad②\)

由 \(①-②\) 得到， \(\cfrac{2}{3}\cdot T_n=\cfrac{1}{3}+\cfrac{1}{3^2}+\cfrac{1}{3^3}+\cdots+\cfrac{1}{3^n}-n\cdot\cfrac{1}{3^{n+1}}\)

则 \(\cfrac{2}{3}\cdot T_n=\cfrac{\frac{1}{3}(1-\frac{1}{3^n})}{1-\frac{1}{3}}-n\cdot\cfrac{1}{3^{n+1}}\)

即 \(\cfrac{2}{3}\cdot T_n=\cfrac{1}{2}(1-\cfrac{1}{3^n})-n\cdot\cfrac{1}{3^{n+1}}\)

则 \(T_n=\cfrac{3}{2}\times\cfrac{1}{2}(1-\cfrac{1}{3^n})-\cfrac{3}{2}\times n\times\cfrac{1}{3^{n+1}}\)\(<\cfrac{3}{4}(1-\cfrac{1}{3^n})=\cfrac{S_n}{2}\)，

故 \(T_{n}<\cfrac{S_n}{2}\) ，证毕 .

〔解后反思〕：从第二问考查了错位相减法和放缩法来看，试题难度提升了。

【2021年高考乙卷文科数学第 \(20\) 题】 已知拋物线 \(C: y^{2}=2px(p>0)\) 的焦点 \(F\) 到准线的距离为 \(2.\)

(1). 求 \(C\) 的方程;

解析: 由题意知， 拋物线的焦点为 \(F(\cfrac{p}{2},0)\)，拋物线的准线为 \(x=-\cfrac{p}{2}\)，

故由 \(\cfrac{p}{2}-(-\cfrac{p}{2})=2\)， 解得 \(p=2\)，

故 \(C\) 的方程为 \(y^{2}=4x\) .

(2). 已知 \(O\) 为坐标原点，点 \(P\) 在 \(C\) 上，点 \(Q\) 满足 \(\overrightarrow{PQ}=9\overrightarrow{QF}\)， 求直线 \(OQ\) 斜率的最大值.

分析：由于题目中涉及到向量的倍数关系，故我们联想到利用向量的坐标来刻画向量，这样我们采用抛物线的参数方程的形式来设点的坐标，就非常方便我们表达求直线 \(OQ\) 斜率。

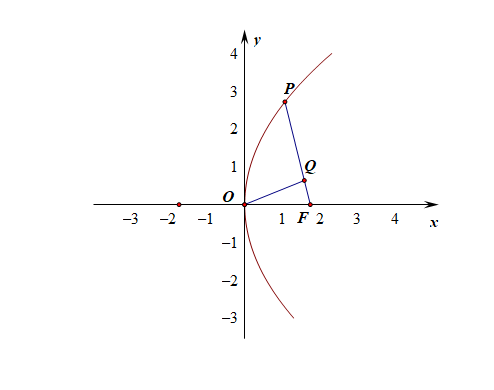
解析：由于 \(C\) 的方程为 \(y^{2}=4x\) ，故设点 \(P(4t^2,4t)\)，\(t\in R\)，

又由于 \(F(1,0)\) ，设点 \(Q(m,n)\) ， 则 \(\overrightarrow{PQ}=(m-4t^2,n-4t)\) ， \(9\overrightarrow{QF}=9(1-m,0-n)\) ，

则由 \(\overrightarrow{PQ}=9\overrightarrow{QF}\)，可得到 \(\left\{\begin{array}{l}{m-4t^2=9-9m}\\{n-4t=-9n}\end{array}\right.\quad\)

解得， \(\left\{\begin{array}{l}{m=\cfrac{2}{5}t^2+\cfrac{9}{10}}\\{n=\cfrac{2}{5}t}\end{array}\right.\quad\)，由于 \(k_{_{OQ}}=\cfrac{n-0}{m-0}\)，

由图可知，当\(t\leqslant 0\)时，点 \(P(4t^2,4t)\) 和点 \(Q(m,n)\) 均在第四象限，不符合题意[当点 \(Q\) 在第四象限时，\(k_{OQ}<0\)，而当点 \(Q\) 在第一象限时，\(k_{OQ}>0\)，直线斜率的最大值可能为正值，故舍弃对\(t\leq0\)的讨论]，故我们只需要讨论 \(t>0\)时的情形即可；
故 \(k_{_{OQ}}\)\(=\)\(\cfrac{\frac{2}{5}t}{\cfrac{2}{5}t^2+\cfrac{9}{10}}\)\(\xlongequal[变量得以集中到分母位置]{分子分母同除以\frac{2}{5}t}\cfrac{1}{t+\cfrac{9}{4t}}\)\(\leqslant \cfrac{1}{2\sqrt{t\cdot\cfrac{9}{4t}}}\)\(=\)\(\cfrac{1}{3}\)，

当且仅当 \(t=\cfrac{3}{2}\)时取到等号；

故 \(k_{_{OQ}}\)的最大值为 \(\cfrac{1}{3}\) .