争鸣|一道有限无限思想题目的思辨

前言

一家之言，难免有挂一漏万之嫌，欢迎各位批评雅正，谢谢合作。

题目列举

【案例】【2018安徽江淮十校联考】有限与无限转化是数学中的一种重要的思想方法。如在《九章算术》方田章圆田术(刘徽注)中：“割之又割以至于不可割，则与圆合体而无所失矣。”说明“割圆术”是一种无限与有限的转化过程，再如\(\sqrt{2+\sqrt{2+\sqrt{2+\cdots}}}\)中“\(\cdots\)”即代表无限次重复，但原式却是个定值\(x\)，这可以通过方程\(\sqrt{2+x}=x\)确定出来\(x=2\)，则\(1+\cfrac{1}{1+\cfrac{1}{1+\cdots}}\)=【\(\qquad\)】

$A.\cfrac{-\sqrt{5}-1}{2}$ $B.\cfrac{\sqrt{5}-1}{2}$ $C.\cfrac{1+\sqrt{5}}{2}$ $D.\cfrac{1-\sqrt{5}}{2}$

解析：令\(1+\cfrac{1}{1+\cfrac{1}{1+\cdots}}=x\)，则左式的分母也就是\(x\)，即原式可以改写为\(1+\cfrac{1}{x}=x\)，

即\(x^2-x-1=0\)，解得\(x=\cfrac{1+\sqrt{5}}{2}\)，其中\(x=\cfrac{1-\sqrt{5}}{2}\)舍去，原因是由表达式可知必有\(x>0\)。

故\(1+\cfrac{1}{1+\cfrac{1}{1+\cdots}}=\cfrac{1+\sqrt{5}}{2}\)，故选\(C\)。

解后反思：上述的解法是现有常见题库中的常见解法，但我们认为有漏洞，不应该舍去负值，以下尝试从两个角度做出说明：

[角度一]：从数的角度证伪如下，为便于计算，我们借助desmos软件的计算功能，

同时定义函数\(f(x)=1+\cfrac{1}{x}\)，相关计算如下：

由上述图形计算器软件可知，当\(x=\cfrac{1\pm \sqrt{5}}{2}\)时，两个值都能满足方程，故选项\(C\)，\(D\)都满足。

[角度二]：从形的角度证伪如下，

首先定义原函数[零次迭代]为\(f(x)=1+\cfrac{1}{x}\)，

则一次迭代\(f(f(x))=1+\cfrac{1}{f(x)}=1+\cfrac{1}{1+\frac{1}{x}}\)，

二次迭代\(f(f(f(x)))=1+\cfrac{1}{f(f(x))}=1+\cfrac{1}{1+\frac{1}{f(x)}}=1+\cfrac{1}{1+\frac{1}{1+\frac{1}{x}}}\)，

三次迭代\(f(f(f(f(x))))=1+\cfrac{1}{f(f(f(x)))}\)\(=1+\cfrac{1}{1+\frac{1}{f(f(x))}}\)\(=1+\cfrac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{x}}}}\)，

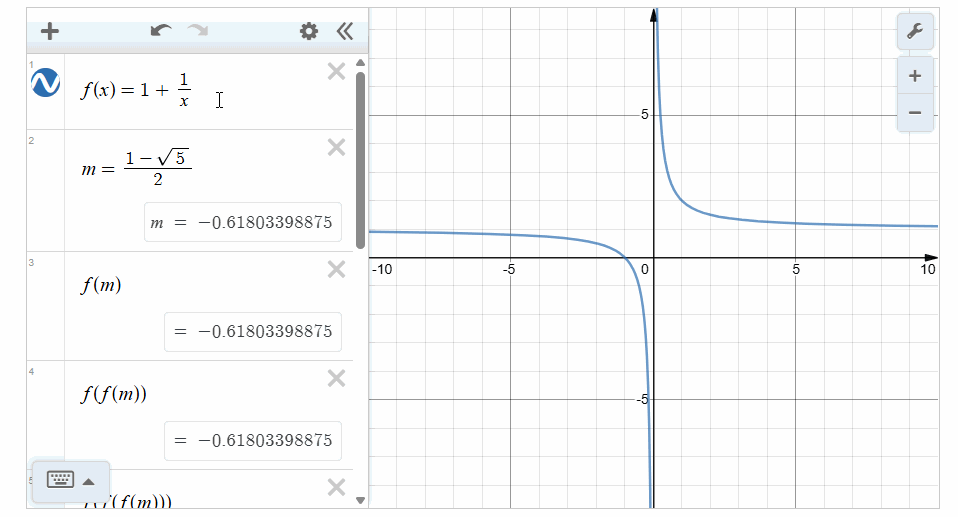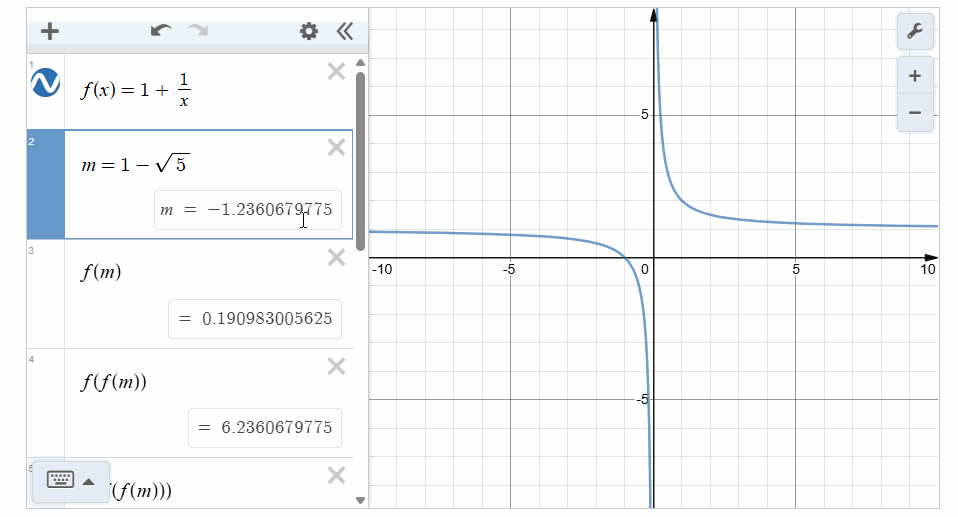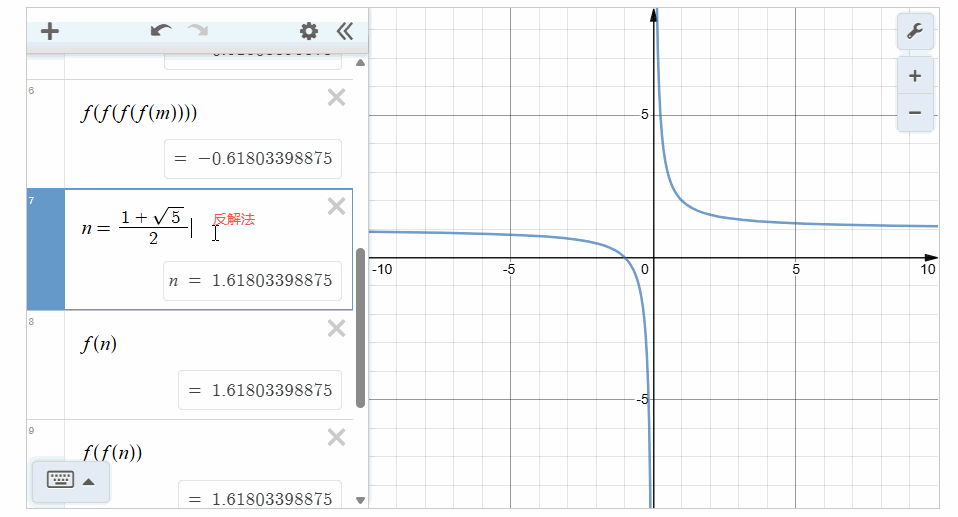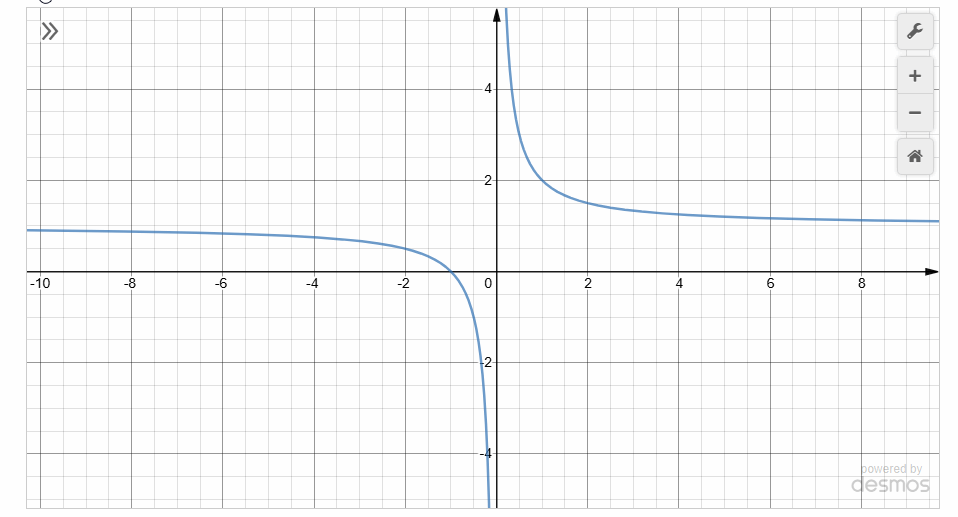
依此类推，\(\cdots\)，直到无限次迭代，观察下图可以看出，

当迭代的次数为偶数次时，函数的图像出现在第Ⅰ、Ⅱ、Ⅲ三个象限内，图像关于直线\(y=-x+1\)对称；

当迭代的次数为奇数次时，函数的图像出现在第Ⅰ、Ⅱ、Ⅲ三个象限内，图像关于直线\(y=-x+1\)对称；

总的来说，函数的任何次迭代的图像都是关于直线\(y=-x+1\)对称；并且这些函数都经过公共点\((\cfrac{\sqrt{5}+1}{2},\cfrac{\sqrt{5}+1}{2})\)和\((\cfrac{1-\sqrt{5}}{2},\cfrac{1-\sqrt{5}}{2})\)，

当我们做出函数\(y=x\)的图像时，很显然函数\(y=x\)和任何次的迭代结果的函数图像始终有两个交点，

其一为\((\cfrac{\sqrt{5}+1}{2},\cfrac{\sqrt{5}+1}{2})\)，其二为\((\cfrac{1-\sqrt{5}}{2},\cfrac{1-\sqrt{5}}{2})\)，

故\(x=\cfrac{\sqrt{5}+1}{2}\)或者\(x=\cfrac{1-\sqrt{5}}{2}\)应该都满足题意；

即两个值都是满足题意的，故选项\(C\)，\(D\)都满足。

相关链接

有限与无限思想