频率分布直方图

前言

✍️ 频率分布直方图的纵轴为什么要用 \(\cfrac{频率}{组距}\) ？

频率分布直方图是一种用于展示数据分布情况的图形表示方法。在这种图表中，数据被分成若干个等宽的区间（组距），每个区间的宽度是固定的。每个区间的频数（即落在该区间内的数据点的数量）被转换成一个矩形的高度，并将这些矩形并排放置以形成直方图。

直方图的纵轴表示的是每个区间的频率或者频率密度。频率是指每个区间内数据点的数量与总数据点数量的比值，而频率密度是频率除以组距。选择频率密度作为纵轴的原因有以下几点：

标准化：由于每个组距的宽度是相同的，频率密度使得不同组的频率可以进行比较。如果只使用频率，那么宽的区间自然比窄的区间拥有更高的频率值，这可能会造成误导。

可比性：频率密度允许不同数据集的直方图之间进行比较。即使它们的组距不同，频率密度也能提供一个统一的比较标准。

连续性：当组距趋于零时，频率密度趋于概率密度函数。这使得直方图可以作为连续概率分布的近似。

面积表示概率：在直方图中，每个矩形的面积代表该区间的概率。如果使用频率密度，那么整个直方图的面积将等于1，这与概率的性质相符合。

便于计算：频率密度的计算通常比频率更简单，因为它直接与数据的分布和组距有关。

因此，使用频率密度而不是单纯的频率作为直方图的纵轴，可以更准确地反映数据的分布情况，并使得不同数据集之间的比较更加公平和直观。

制作步骤

①求极差；②决定组距与组数；③将数据分组；④列频率分布表；⑤画频率分布直方图；

频率分布直方图的特点

①直方图中相邻两横坐标之差表示组距，纵轴表示\(\cfrac{频率}{组距}\)，\(频率=\cfrac{频率}{组距}\times 组距\)，

②频率分布直方图中各小长方形的面积(频率)之和为\(1\)，各小长方形高之比也就是频率比。

③频率分布表和频率分布直方图是一组数据频率分别的两种形式，前者准确，后者直观。

平均数、众数与中位数从不同的角度描述了一组数据的集中趋势；平均数是从平均水平的角度刻画集中趋势；众数是从相同数据出现的次数多少刻画集中趋势；中位数是从数据[由小到大的顺序]出现的位置刻画的集中趋势；

方差与标准差描述其波动大小，单位有区别；

使用角度

从形的角度

从数的角度

频率分布直方图中的数字特征的计算

当一组数据经过加工整理成频率分布直方图后，数据信息会有所损失，所以计算数据的数字特征有一定的难度。

①众数：直方图中最高矩形的中点横坐标；解释：众数是指出现次数最多的数，若同一组内的数据出现次数越多，则这组的组距对应的矩形的高度自然是最高的；如果此时我们要挑选一个数据来代表这组数据，那么选区间左端点的值未免太小，选右端点的值未免太大，比较理想和中庸的做法是取两个端点数据的平均数来做代表，故众数是直方图中最高矩形的底边中点横坐标；

②中位数：频率分布直方图频率和(面积和)的一半处所对应的横坐标，即面积等分线所对应的横坐标；相关解释：中位数即第 \(50\) 百分位数或 \(50\%\) 分位数，小于等于这个数的频数或频率是 \(50\%\)，大于等于这个数的频数或频率是 \(50\%\)，故中位数为频率或面积等分线所对应的横坐标；注意频率分布直方图中的中位数往往需要计算才能得到 . 中位数的拓展,百分位数，其计算往往是个难点。

③平均数：每个矩形的分组的中点值乘以每个对应矩形的面积再求和；^[1]

④方差：每个矩形的分组的中点值与平均值的差的平方与频率乘积，再求和；^[2]

⑤标准差：方差的算术平方根；

【2018·课标全国I第19题】某家庭记录了未使用节水龙头\(50\)天的日用水量数据（单位：\(m^3\)）和使用了节水龙头\(50\)天的日用水量数据，得到频数分布表如下：

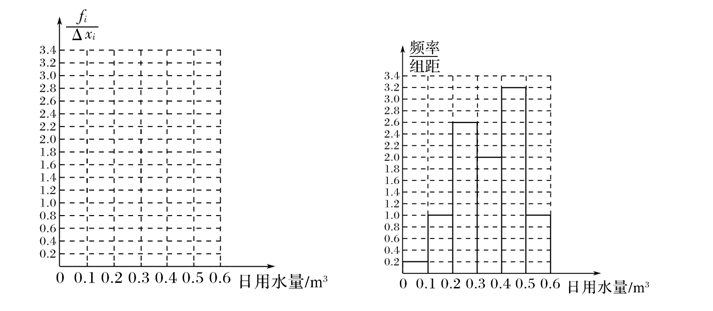
未使用节水龙头50天的日用水量频数分布表

日用水量	\([\)\(0\),\(0.1\)\()\)	\([\)\(0.1\),\(0.2\)\()\)	\([\)\(0.2\),\(0.3\)\()\)	\([\)\(0.3\),\(0.4\)\()\)	\([\)\(0.4\),\(0.5\)\()\)	\([\)\(0.5\),\(0.6\)\()\)	\([\)\(0.6\),\(0.7\)\()\)
频数	\(1\)	\(3\)	\(2\)	\(4\)	\(9\)	\(26\)	\(5\)

使用了节水龙头50天的日用水量频数分布表

日用水量	\([\)\(0\),\(0.1\)\()\)	\([\)\(0.1\),\(0.2\)\()\)	\([\)\(0.2\),\(0.3\)\()\)	\([\)\(0.3\),\(0.4\)\()\)	\([\)\(0.4\),\(0.5\)\()\)	\([\)\(0.5\),\(0.6\)\()\)
频数	\(1\)	\(5\)	\(13\)	\(10\)	\(16\)	\(5\)

(1). 在下图中作出使用了节水龙头50天的日用水量数据的频数分布直方图 .

【2017高考真题卷Ⅱ文科19题改编】【题文】如图所示，求该频率分布直方图的众数、中位数、平均数、方差。

考点：频率分布直方图，众数、中位数、平均数、方差；以上图为例，

• 求众数：

“旧养殖法”的众数为\(47.5\)；“新养殖法”的众数为\(52.5\)；

• 求中位数[以旧养殖法的为例即可]

法一：利用方程求解，对于旧养殖法而言，由于 \(25-45\) 之间的面积和为 \(0.42<0.50\)， \(25-50\)之间的面积和为 \(0.62>0.50\)，故中位数一定位于 \(45-50\) 之间，设中位数为 \(x\) ，则 \(0.42+(x-45)\times0.04=0.50\) ，求得 \(x=47\) ，即中位数为 \(47\) 。

法2：利用比例求解，对于旧养殖法而言，由于 \(25-45\) 之间的面积和为 \(0.42<0.50\)， \(25-50\)之间的面积和为 \(0.62>0.50\)，故中位数一定位于 \(45-50\) 之间，故中位数为 \(45+\cfrac{0.5-0.42}{5\times 0.04}\times 5= 47\)，解释：设从 \(45\) 到中位数处的宽度为 \(x\)，则 \(\cfrac{0.5-0.42}{5\times 0.04}=\cfrac{x}{5}\) ，即可表示为 \(x=\cfrac{0.5-0.42}{5\times 0.04}\times 5\).

• 求平均数：比如“旧养殖法”的平均数的计算

\(\bar{x}=27.5\times5\times0.012+32.5\times5\times0.014+37.5\times5\times0.024\)

\(+42.5\times5\times0.034+47.5\times5\times0.040+52.5\times5\times0.032\)

\(+57.5\times5\times0.020+62.5\times5\times0.012+67.5\times5\times0.012\)

\(=47.1\)；

“新养殖法”的平均数的计算

\(\bar{y}=37.5\times5\times0.004+42.5\times5\times0.020+47.5\times5\times0.044\)

\(+52.5\times5\times0.068+57.5\times5\times0.046\)

\(+62.5\times5\times0.010+67.5\times5\times0.008\)

\(=52.35\)；

求方差：比如“新养殖法”的方差计算

\(S^2=(37.5-52.35)^2\times 0.004\times 5+(42.5-52.35)^2\times 0.020\times 5+(47.5-52.35)^2\times 0.044\times 5\)

\(+(52.5-52.35)^2\times 0.068\times 5+(57.5-52.35)^2\times 0.046\times 5\)

\(+(62.5-52.35)^2\times 0.010\times 5+(67.5-52.35)^2\times 0.008\times 5\)

\(=?\)

【2017全国卷2文科19题理科18题高考真题】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量（单位：kg）, 其频率分布直方图如下：

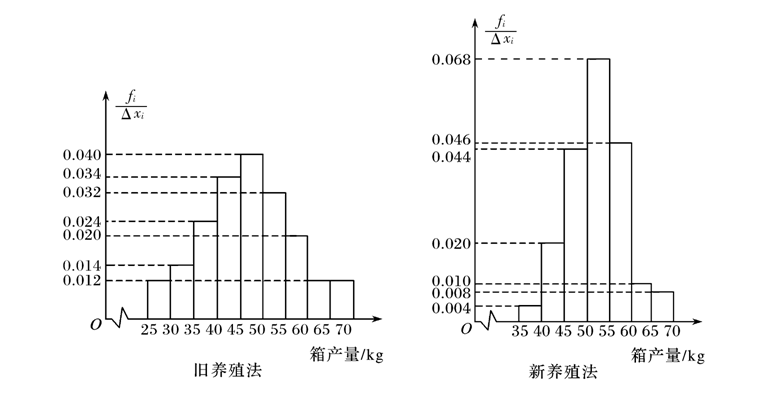
（1）记\(A\)表示事件“旧养殖法的箱产量低于50kg”，估计\(A\)的概率；

分析：本题实质是考查用频率估计概率，所以要会根据频率分布直方图计算频率。

由于“旧养殖法的箱产量低于50kg”的频率为\((0.012+0.014+0.024+0.034+0.040)\times 5=0.62\)，

故所求概率\(P(A)=0.62\)。

同理得到“新养殖法的箱产量低于50kg”的频率为\((0.004+0.020+0.044)\times 5=0.34\)

（2）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关，参考数据表格如下：

$\begin{array}{c|lcr} P(\chi^2\ge k_0) & 0.050 &0.010 &0.001 \\ \hline k_0 & 3.841 & 6.635 & 10.828 \end{array}$ 分析：由上问可知，“旧养殖法的箱产量低于50kg”的频数为$100\times 0.62=62$，

则“旧养殖法的箱产量不低于\(50kg\)”的频数为\(100-62=38\)，

“新养殖法的箱产量低于\(50kg\)”的频数为\(100\times 0.34=34\)，

则“新养殖法的箱产量不低于\(50kg\)”的频数为\(100-34=66\)，由此得到二列联表如下：

\(\qquad\)	箱产量(<50kg)	箱产量($\geqslant$50kg)	总计
旧养殖法	\(62\)\((a)\)	\(38\)\((b)\)	\(100\)\((a+b)\)
新养殖法	\(34\)\((c)\)	\(66\)\((d)\)	\(100\)\((c+d)\)
总计	\(96\)\((a+c)\)	\(104\)\((b+d)\)	\(200\)\((a+b+c+d)\)

由上表计算得到\(\chi^2=\cfrac{n(ad-bc)^2}{(a+b)(c+d)(a+c)(b+d)}\)

\(=\cfrac{200(62\times 66-38\times 34)^2}{(62+38)(34+66)(62+34)(38+66)}=15.705>6.635\)

故有99%以上的把握认为，二者有关联。

（3）根据箱产量的频率分布直方图，对这两种养殖方法的优劣进行比较。

分析：本题目的难点有：到底从哪些角度进行比较？每一个角度下的数值的计算方法。

数据的极差：旧，\(25-70\)；新，\(35-70\)，极差反映了数据的取值范围和数据的几种程度，当然误差是有的；

数据的众数：旧，\(47.5\)；新，\(52.5\)，众数反映了出现次数最多，

数据的平均数：旧，\(47.1\)；新，\(52.35\)，平均数反映了一组数据的平均水平，

数据的方差(标准差)：比较精确的反映了数据的分散和集中程度，将这种程度数量化了。

本题目从运算量和问题出发，可以从数据的范围和数据的中位数(或均值)两个角度作答。

“旧养殖法”的数据分布在\(25-70\)之间，“新养殖法”的数据分布在\(35-70\)之间，

故从数据范围来看，新养殖法的数据更集中，优于旧养殖法；

“旧养殖法”的平均数(中位数)分布在\(40-45\)之间，“新养殖法”的平均数(中位数)分布在\(50-55\)之间，

从平均数(中位数)角度来看，新养殖法也优于旧养殖法。

关联实际

• 问选手水平高低，需要比较平均数；

• 问选手发挥如何，需要比较方差，

• 给定一个考试成绩，问此人考的怎么样？ 可以将该成绩与样本的中位数比较，也可以将该成绩与样本平均数比较；

---

1. 引例，给定数据\(2，2，4，4，4\)，求其平均数；
   \(\bar{x}=\cfrac{2+2+4+4+4}{5}=\cfrac{2\times 2+4\times 3}{5}\)\(=2\times \cfrac{2}{5}+4\times \cfrac{3}{5}\)，
   注释：表达式中的 \(\cfrac{2}{5}\) 和 \(\cfrac{3}{5}\) 的含义分别是样本数据 \(2\) 和 \(4\) 的频率。 \(\cfrac{频数}{样本容量}=频率\)。
   回归到上述解释，每个矩形的分组的中点值是样本数据，每个对应矩形的面积即是频率 . ↩︎

2. 引例，给定一组样本数据\(2，2，4，4，4\)，求这组数据的方差。
   解析：先求平均数为 \(\bar{x} =\cfrac{2+2+4+4+4}{5}=3.2\)；
   则方差为\(s^2=\cfrac{1}{5}[(2-3.2)^2\times 2+(4-3.2)^2\times 3]=(2-3.2)^2\times\cfrac{2}{5}+(4-3.2)^2\times\cfrac{3}{5}\)； ↩︎