求平均数的几个层次

前言

提起平均数，我们一般感觉不是很难，但是若融合到其他的数学素材中，就有了不同的外在表现形式，我们感觉也有了一定的难度，本博文针对平均数的考察方式，分几个层次加以综述：

常见层次

层次一：给定一组数据计算平均数；

• 不带权重的平均数计算；

给定数据\(1，2，3，4，5\)，求其平均数；

分析：\(\bar{x}=\cfrac{1+2+3+4+5}{5}=3\)，

• 带有权重的平均数计算；

给定数据\(2，2，4，4，4\)，求其平均数；

\(\bar{x}=\cfrac{2+2+4+4+4}{5}=\cfrac{2\times 2+4\times 3}{5}\)\(=2\times \cfrac{2}{5}+4\times \cfrac{3}{5}\)，

注释：表达式中的 \(\cfrac{2}{5}\) 和 \(\cfrac{3}{5}\) 的含义就是 \(\cfrac{频数}{样本容量}=频率\)。

• 数学期望，就是带有权重的平均数。

比如，某随机变量 \(X\) 的分布列为

\(X\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)
\(P\)	\(\cfrac{1}{625}\)	\(\cfrac{12}{125}\)	\(\cfrac{12}{25}\)	\(\cfrac{48}{125}\)	\(\cfrac{24}{625}\)

所以随机变量 \(X\) 的数学期望 \(E(X)=1\times\cfrac{1}{625}\)\(+\)\(2\times\cfrac{12}{125}\)\(+\)\(3\times\cfrac{12}{25}\)\(+\)\(4\times\cfrac{48}{625}\)\(+\)\(5\times\cfrac{24}{625}\)\(=\)\(\cfrac{2101}{625}\).

层次二，利用频率分布直方图计算平均数；

【2017高考真题卷Ⅱ文科19题改编】如图所示，求该频率分布直方图的平均数；

解析：

比如“旧养殖法”的平均数的计算

\(\bar{x}=27.5\times5\times0.012+32.5\times5\times0.014+37.5\times5\times0.024\)

\(+42.5\times5\times0.034+47.5\times5\times0.040+52.5\times5\times0.032\)

\(+57.5\times5\times0.020+62.5\times5\times0.012+67.5\times5\times0.012\)

\(=47.1\)；

“新养殖法”的平均数的计算

\(\bar{y}=37.5\times5\times0.004+42.5\times5\times0.020+47.5\times5\times0.044\)

\(+52.5\times5\times0.068+57.5\times5\times0.046\)

\(+62.5\times5\times0.010+67.5\times5\times0.008\)

\(=52.35\)；

层次三，带有概率的频率分布直方图计算平均数；

【选自2021届黄冈八模测试卷一第19题】小明每天从家步行去学校，有两条路线可以选择，第一条路线，需走天桥，不用等红灯，平均用时 \(910\) 秒；第二条路线，要经过两个红绿灯路口，如图，

\(A\) 处为小明家，\(D\) 处为学校，走路段 \(AB\) 需 \(240\) 秒，在 \(B\) 处有一红绿灯，红灯时长 \(120\) 秒，绿灯时长 \(30\) 秒，走路段 \(BC\) 需 \(450\) 秒；在 \(C\) 处也有一红绿灯，红灯时长 \(100\) 秒，绿灯时长 \(50\) 秒，走路段 \(CD\) 需 \(200\) 秒，小明进行了 \(60\) 天的试验，每天都选择第二条路线，并记录了在 \(B\) 处等待红灯的时长，经统计， \(60\) 天中有 \(48\) 天在 \(B\) 处遇到红灯，根据记录的 \(48\) 天等待红灯时长的数据绘制了下面的频率分布直方图。已知 \(B\) 处和 \(C\) 处的红灯亮起的时刻恰好始终保持相同，且红绿灯之间切换无时间间隔。

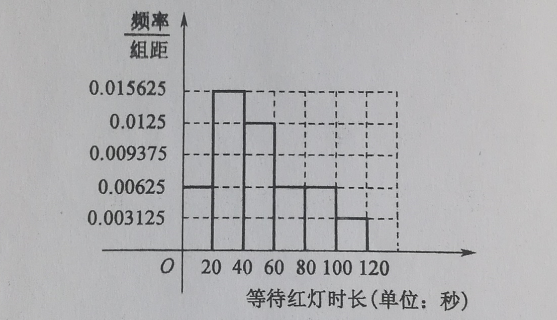
(1). 若小明选择第二条路线，设当小明到达 \(B\) 处的时刻为 \(B\) 处红灯亮起后的第 \(x\) 秒（\(0≤x<150\))时，小明在 \(B\) 处等待红灯的时长为 \(y\) 秒，求 \(y\) 关于 \(x\) 的函数的解析式.

分析：由题意，\(y\) 是 \(x\) 的一次型函数，又由于当 \(x=0\) 时，应该有 \(y=120\)，当 \(x=120\) 时，应该有 \(y=0\)，

故在等红灯阶段有 \(y=120-x\)；综上得到，

\(y=\left\{\begin{array}{l}120-x, &0 \leqslant x<120 \\ 0,&120 \leqslant x<150\end{array}.\right.\)

(2). 若小明选择第二条路线，请估计小明在 \(B\) 处遇到红灯的概率，并问小明是否可能在 \(B\) 处和 \(C\) 处都遇到红灯.

分析：估计小明在 \(B\) 处遇到红灯的概率为 \(\cfrac{48}{60}=\cfrac{4}{5}\) 注意此处的关键词【估计】，其含义是用样本容量\(60\)里面出现红灯的频率来估计总体，即以后的任何一天在\(B\)处遇到红灯的概率，涉及的是用样本的数字特征来估计总体的数字特征；\(\quad\)；

由于小明过 \(B\) 处的时刻一定是 \(B\) 处红灯亮起 \(120\) 秒后， 而 \(B\) 和 \(C\) 处的红灯亮起的时刻恰好始终保持相同且 \(B\) 处和 \(C\) 处红绿灯的时长之和相等，\(120+30\)\(=\)\(100+50\)，都等于小明走路段 \(BC\) 所需的时间 \(450\) 秒的 \(\cfrac{1}{3}\)，所以小明到达 \(C\) 处的时刻一定是 \(C\) 处红灯亮起 \(120\) 秒之后， 而此时已经是 \(C\) 处绿灯亮了 \(20\) 了，故小明不会在 \(C\) 处遇到红灯， 因此小明不可能在 \(B\) 处和 \(C\) 处都遇到红灯.

(3). 若取区间中点作为该区间对应的等待红灯的时长，以这两条路线的平均用时作为决策依据，小明应选择哪一条路线?

分析：小明走第二条路线平均等待红灯的时长，即利用频率分布直方图求平均值；此处又由于涉及碰到红灯和绿灯的概率不一致，故

小明走第二条路线平均等待红灯的时长

\((10\times 0.00625\) \(+30\times 0.015625\)\(+\)\(50\times 0.0125+\)\(70\times 0.00625\)\(+\)\(90\times 0.00625\)\(+\)\(110 \times 0.003125\)\()\times 20\)\(\times\cfrac{4}{5}+0\times\cfrac{1}{5}=40\) (秒)，

小明走第二条路线平均用时为 \(240+450+200+40=930\) (秒)，由于 \(930>910\) ， 故小明应该选择第一条路线.

运算技巧

比如计算数据\(515，521，527，531，532，536，543，548，558，559\)的平均数。

\(\bar{x}=\cfrac{515+521+527+531+532+536+543+548+558+559}{10}=537\)；

\(\bar{x}=\cfrac{500+15+500+21+500+27+500+31+500+32}{10}+\) \(\cfrac{500+36+500+43+500+48+500+58+500+59}{10}\)\(=537\)；

\(\bar{x}=500+\cfrac{15+21+27+31+32+36+43+48+58+59}{10}=537\)；

\(\bar{x}=540+\cfrac{-25-19-13-9-8-4+3+8+18+19}{10}=540+\cfrac{-30}{10}=537\)；

某班级的 \(33\) 名学生的某日跑步里程如下表所示：

人数	\(1\)	\(1\)	\(2\)	\(1\)	\(5\)	\(3\)	\(20\)
跑步里程	\(5500\)	\(5000\)	\(3500\)	\(3000\)	\(2500\)	\(2000\)	\(1500\)

求该班级该日跑步里程的平均数、中位数、众数(精确到整数).

解析：中位数是 \(1500\) 米，众数是 \(1500\) 米，

平均数的计算如下：

\(\bar{x}=1500+\cfrac{1}{33}(4000+3500+2000\times2+1500+1000\times5+500\times3+0\times20)\approx 1500+591=2091\) 米。

〔解后反思〕当然也可以这样计算，求和的基准尽量选择最大的频数对应的数据，

\(\bar{x}=2500+\cfrac{1}{33}(3000+2500+1000\times2+500+0\times5-500\times3-1000\times20)\approx 2500-409=2091\) 米。