定义域值域习题

前言

相关链接

1、求函数的定义域；

2、求函数的值域；

典例剖析

【2019贵阳检测】下列函数中，同一个函数的定义域和值域相同的函数是【】

$A.y=\sqrt{x-1}$ $B.y=lnx$ $C.y=\cfrac{1}{3^x-1}$ $D.y=\cfrac{x+1}{x-1}$

分析：对于选项\(A\)，函数\(y=\sqrt{x-1}\)，由\(x-1\geqslant 0\)得到定义域为\([1,+\infty)\)，类比函数\(y=\sqrt{x}\)，可知其值域为\([0,+\infty)\)；故不选\(A\);

对于选项\(B\)，函数\(y=lnx\)，定义域为\((0,+\infty)\)，值域为\(R\)；故不选\(B\);

对于选项\(C\)，函数\(y=\cfrac{1}{3^x-1}\)，由\(3^x-1\neq 0\)得到\(3^x\neq 1=3^0\)，故定义域为\((-\infty,0)\cup (0,+\infty)\)，求解值域时可以这样作，令\(3^x-1=t\)，则可知\(t>-1\)，故原函数的值域等价于求\(y=\cfrac{1}{t}(t>-1)\)的值域，可知其值域为\((-\infty，-1)\cup (0,+\infty)\)；故不选\(C\);

对于选项\(D\)，函数\(y=y=\cfrac{x+1}{x-1}\)，由\(x-1\geqslant 0\)得到定义域为\((-\infty，1)\cup (1,+\infty)\)，又\(y=\cfrac{x+1}{x-1}=1+\cfrac{2}{x-1}\)，由于\(\cfrac{2}{x-1}\neq 0\)，故\(y\neq 1\)，可知其值域为\((-\infty，1)\cup (1,+\infty)\)，故选\(D\);

【已知定义域或值域为\(R\)求参数的取值范围】已知函数\(f(x)=ln(x^2+2ax-a)\)，

①如果函数的定义域是\(R\)，求参数\(a\)的取值范围；

预备：先想一想，这个函数的定义域应该怎么求解？

分析：由于函数的定义域是\(R\)，说明对任意的\(x\in R\)，都能使得\(g(x)=x^2+2ax-a>0\)，

转化为二次函数恒成立问题了，(此时至少可以考虑数形结合或者恒成立分离参数)

这里用数形结合，函数\(g(x)\)开口向上，和\(x\)轴没有交点，则\(\Delta <0\)，

即\(\Delta=(2a)^2-4\times 1\times(-a)<0\)，解得\(a\in (-1，0)\)。

②如果函数的值域是\(R\)，求参数\(a\)的取值范围；

分析：如右图所示，要使得函数\(f(x)\)的值域是\(R\)，说明内函数\(g(x)=x^2+2ax-a\)必须要能取遍所有的正数，结合下图，

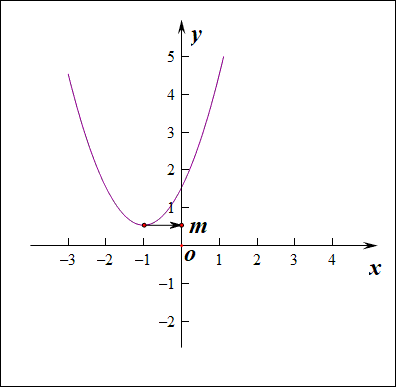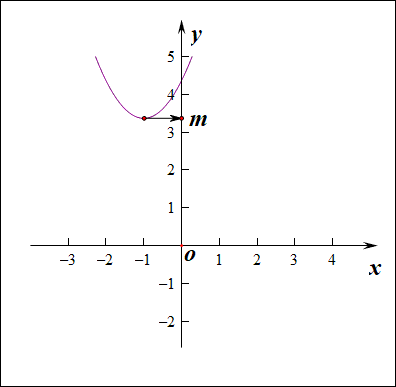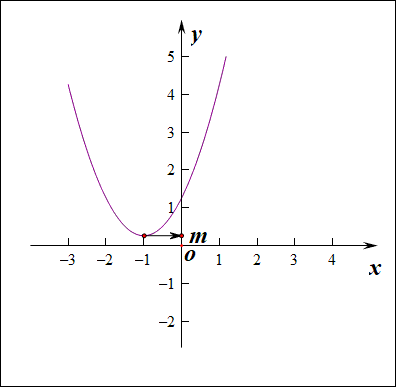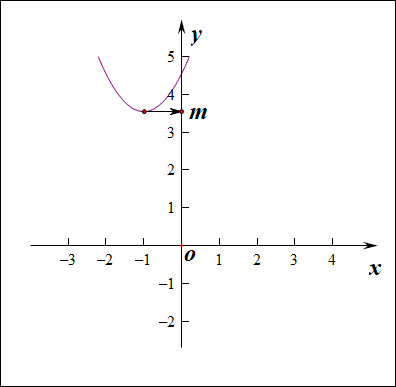
如果有一部分正实数不能取到，那么函数\(f(x)\)的值域就不会是\(R\)，这样只能是函数\(g(x)\)的\(\Delta \ge 0\)，

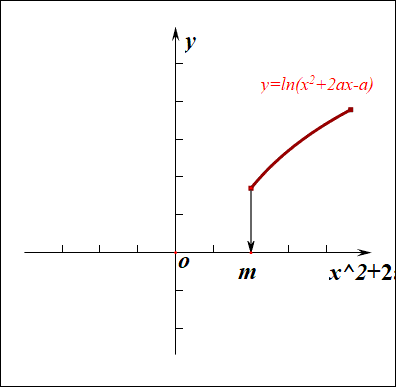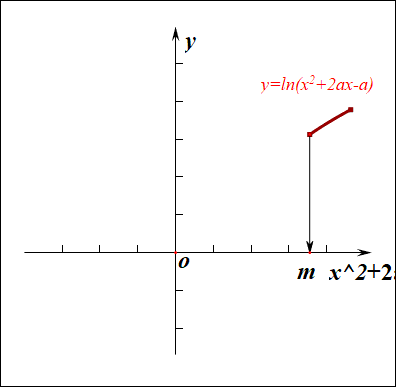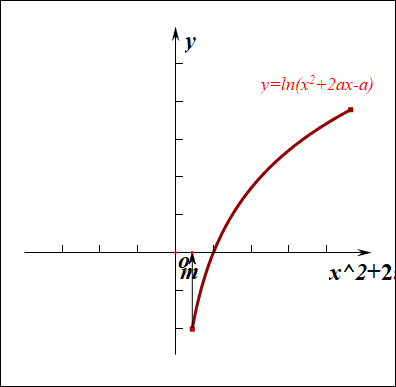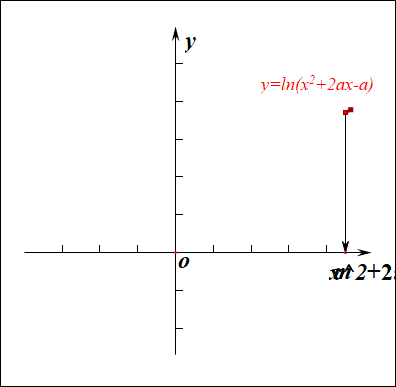
而不能是\(\Delta <0\)，注意现在题目要求是值域为\(R\)，而不是定义域为\(R\)，

因此必须满足条件\(\Delta=(2a)^2-4\times 1\times(-a)\ge 0\)，解得\(a\in \{a\mid a\leq -1 ，a\ge 0\}\)。

下图是参数\(a\in [-3，3]\)时的两个函数图像的动态变化情况；

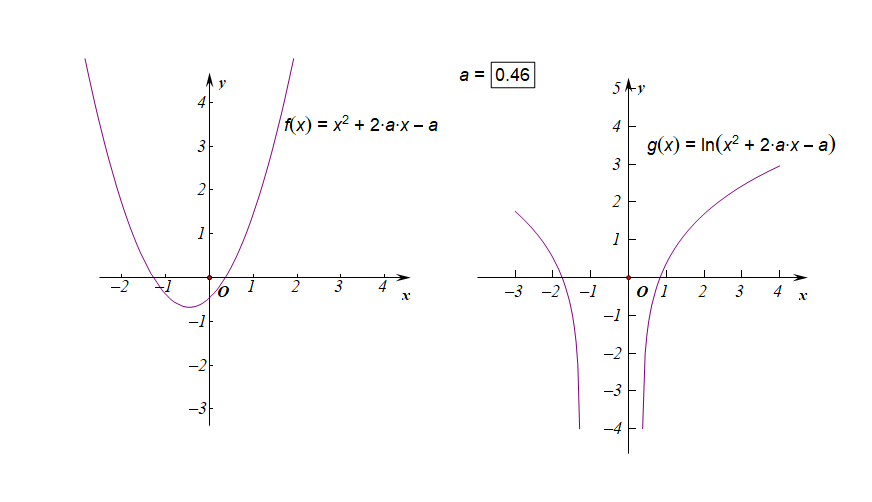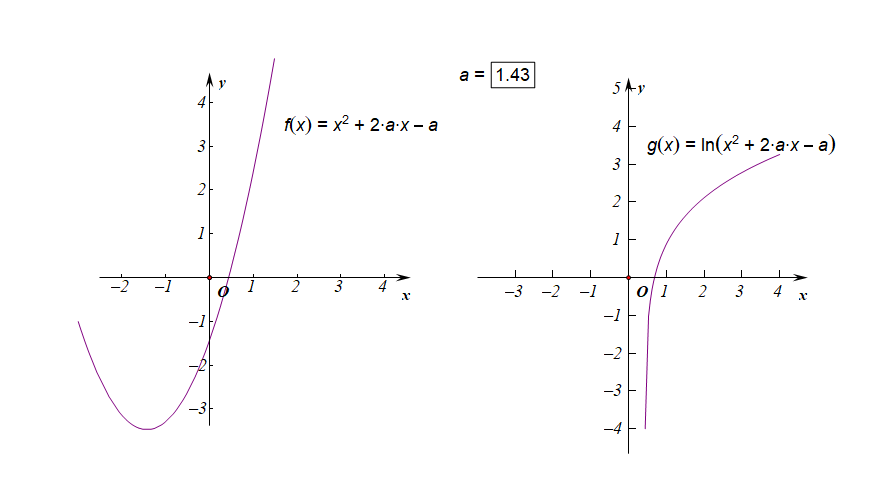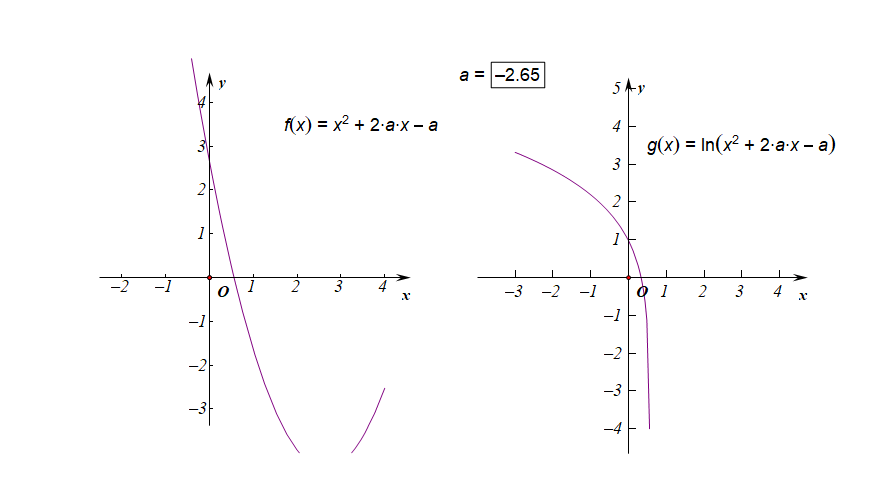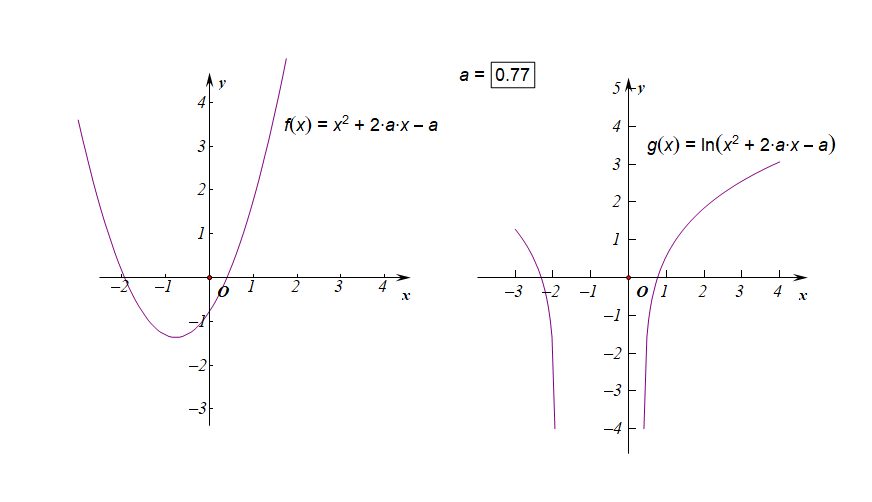
下图是参数\(a\in (-1，0)\)时的两个函数图像的动态变化情况；

【已知定义域或值域为\(R\)求参数的取值范围】【2018浙江名校协作体考试】函数\(y=\sqrt{2ax^2+4x+a-1}\)的值域为\([0，+\infty)\)，则\(a\)的取值范围是____________。

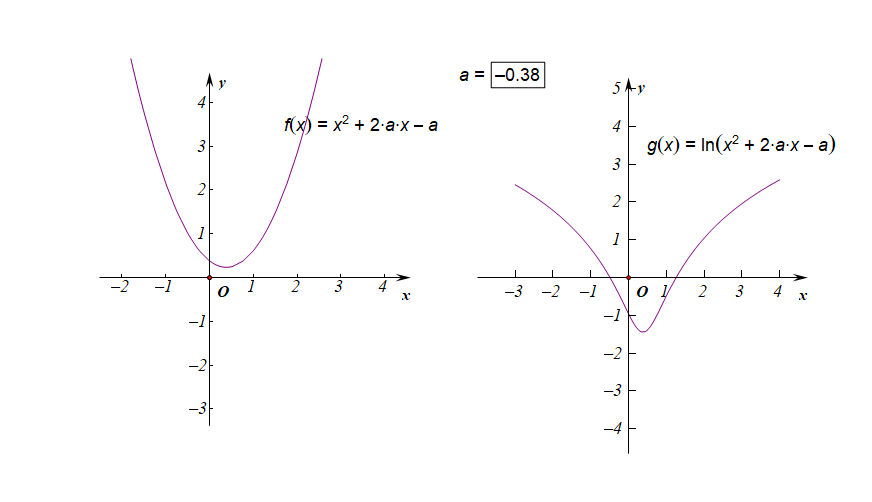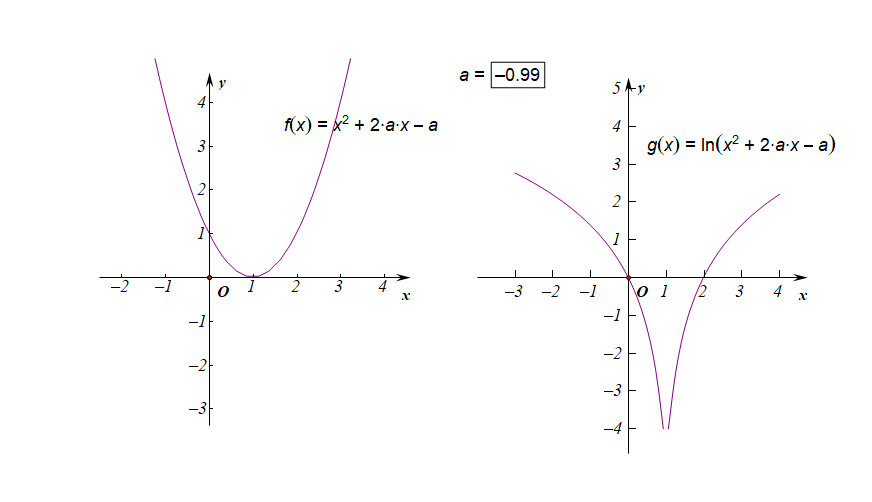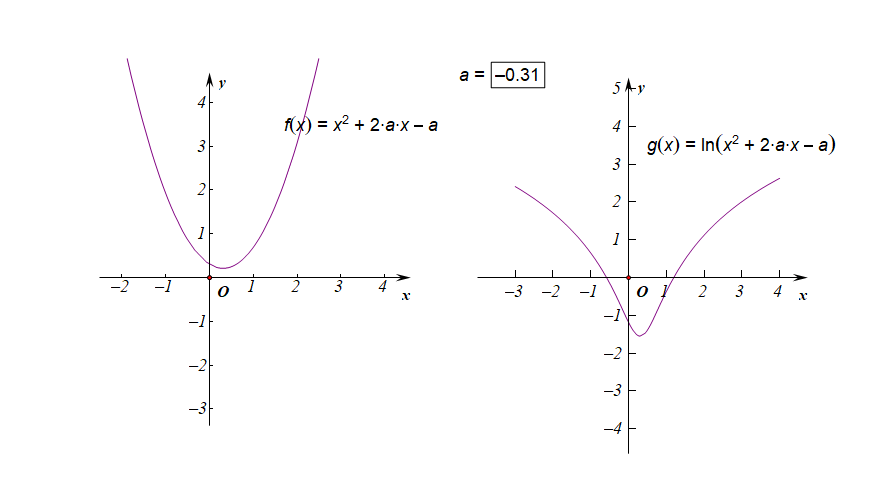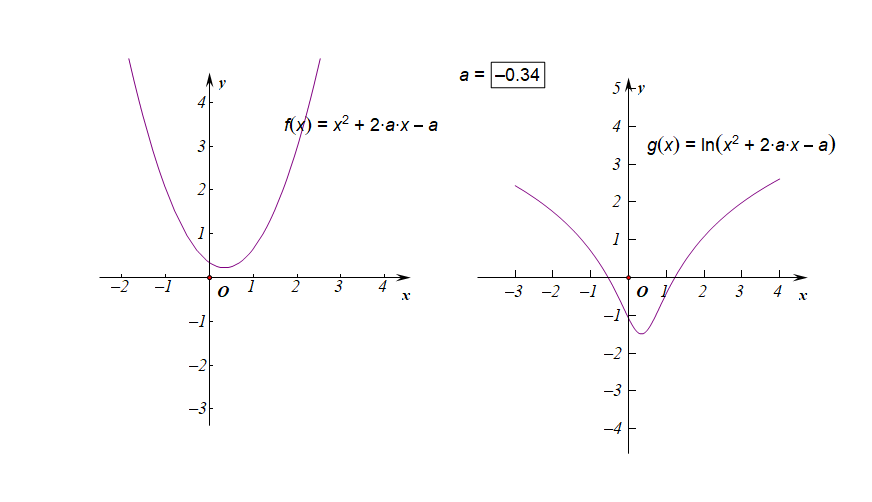
分析：令\(u=2ax^2+4x+a-1\)，则\(u\)是\(x\)的仿二次函数，

①当\(a=0\)时，\(u=4x\)，则当\(x\geqslant 0\)时，\(u\geqslant 0\)能满足，故值域为\([0，+\infty)\)，此时满足题意。

②当\(a>0\)时，必须\(\Delta \geqslant 0\)才能满足值域为\([0，+\infty)\)由于被开方数必须大于等于零，故好多学生此时容易错想为\(\Delta \leqslant 0\)，这是错误的，此时我们不能也不应该保证定义域为 R，而必须保证值域为 R；，

故由\(\left\{\begin{array}{l}{a>0}\\{\Delta=16-4\times2a(a-1)}\geqslant 0\end{array}\right.\) 解得\(0<a\leqslant 2\)，

综上可知，\(a\in [0，2]\).

【2019衡阳四中月考】若函数\(y=\sqrt{a-a^x}(a>0，a\neq 1)\)的定义域和值域都是\([0,1]\)，则\(log_a\frac{5}{6}+log_a\frac{48}{5}\)=_______

分析：由题意可得，\(a-a^x\geqslant 0\)，又定义域是\([0,1]\)，可得\(a>1\)，

则\(y=\sqrt{a-a^x}\)在定义域\([0,1]\)上单调递减，又由于值域是\([0,1]\)，则\(f(0)=\sqrt{a-1}=1\)，\(f(1)=0\)，

所以得到\(a=2\)，代入\(log_a\frac{5}{6}+log_a\frac{48}{5}=log_28=3\).

函数\(y＝f(x)\)的图像如图所示，那么\(f(x)\)的定义域是________；值域是________；其中只有唯一的\(x\)值与之对应的\(y\)值的范围是________．

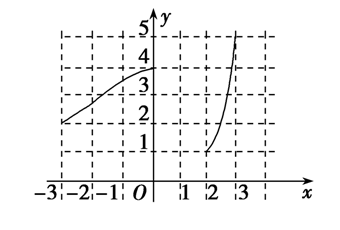
分析：定义域为\([-3,0]\cup [2,3]\)；值域是\([1,5]\)；

只有唯一的\(x\)值与之对应的\(y\)值的范围是\([1,2)\cup(4,5]\)；