导数中的题型和破解思路01
前言
知识储备
-
本节用到的数学思想:分类讨论;转化划归;数形结合;函数与方程;
-
本节用到的数学方法:导数法,多项式除法,试商法,分组分解法,分离参数法,
-
恒成立、能成立类命题
题型结构图1
题型归类
【题型Ⅰ】求曲线\(f(x,y)=0\)或函数\(y=f(x)\)的切线
- 类型1:一曲线一直线的单切线形
思路方法:若是在点处,利用点斜式写出切线方程:\(y-f(x_0)=f'(x_0)(x-x_0)\);若是过点处,则设切点\((x_0,y_0)\),然后利用方程组求切点,再代入计算切线即可。
分析:利用点斜式来求解,
其中斜率\(k=f'(x)_{|x=1}=(2x-\cfrac{1}{x^2})_{|x=1}=1\),切点是\((1,2)\),
故切线方程为\(y-2=1(x-1)\),整理为\(y=x+1\)。
分析:设经过点\(P(2,4)\)的切线方程与曲线相切于点\(P_0(x_0,y_0)\),则有
\(\begin{cases}y_0=\cfrac{1}{3}x_0^3+\cfrac{4}{3}\\ k=f'(x_0)=x_0^2\\ y-y_0=f'(x_0)(x-x_0) \end{cases}\)
又因为点\(P(2,4)\)在切线方程上,则有\(4-(\cfrac{1}{3}x_0^3+\cfrac{4}{3})=x_0^2(2-x_0)\)
整理得到,\(x_0^3-3x_0^2+4=0\)
\(x_0^3-3x_0^2+4=(x_0^3+1)-3(x_0^2-1)\)
\(=(x_0+1)(x_0^2-x_0+1)-3(x_0+1)(x_0-1)\)
\(=(x_0+1)(x_0^2-x_0+1-3x_0+3)\)
\(=(x_0+1)(x_0-2)^2=0\);
即\((x_0+1)(x_0-2)^2=0\),解得\(x_0=-1\),或\(x_0=2\)
当\(x_0=-1\)时,切点为\((-1,1)\),\(k_1=1\),切线方程为\(x-y+2=0\);
当\(x_0=2\)时,切点为\((2,4)\),\(k_2=4\),切线方程为\(4x-y-4=0\);
注意:常用的变形方法有试商法、分组分解法、多项式除法;
- 类型2:两曲线一直线的公切线型
思路方法:转化为一曲线和一直线型;或者利用同一法求解
分析:本题目属于公切线问题,可以先求得过点\((1,0)\)处的与\(y=x^3\)相切的直线,然后联立该直线和抛物线(二次函数),利用\(\Delta=0\)来保证另一个相切的成立。
解析:设过点\((1,0)\)的直线与曲线\(y=x^3\)相切于点\((x_0,y_0)\),由\(f'(x)=3x^2\)可得,
\(\begin{cases}k=f'(x_0)=3x_0^2\\y_0=x_0^3\\y-y_0=f'(x_0)(x-x_0)\end{cases}\),又点\((1,0)\)在切线上,故有\(0-x_0^3=3x_0^2(1-x_0)\),
解得\(x_0=0\)或\(x_0=\cfrac{3}{2}\);
当\(x_0=0\)时,\(y_0=0\),即切点是\((0,0)\),斜率\(k=0\),故切线方程为\(y=0\),
与曲线\(y=ax^2+\cfrac{15}{4}x-9\)相切,消\(y\)得到\(ax^2+\cfrac{15}{4}x-9=0\),
利用\(\Delta=(\cfrac{15}{4})^2+4\times 9a=0\),解得\(a=-\cfrac{25}{64}\);
当\(x_0=\cfrac{3}{2}\)时,\(y_0=\cfrac{27}{8}\),即切点是\((\cfrac{3}{2},\cfrac{27}{8})\),斜率\(k=\cfrac{27}{4}\),
故切线方程为\(y-\cfrac{27}{8}=\cfrac{27}{4}(x-\cfrac{3}{2})\),
与曲线\(y=ax^2+\cfrac{15}{4}x-9\)相切,消\(y\)得到\(ax^2-3x-\cfrac{9}{4}=0\),
利用\(\Delta=(-3)^2-4\times a\times(-\cfrac{9}{4})=0\),解得\(a=-1\);
综上,\(a=-1\)或\(-\cfrac{25}{64}\),故选A。
反思总结:直线与三次曲线的相切问题,我们用导数解决;直线与二次曲线(如圆、椭圆、双曲线、抛物线等)的相切问题,我们常用\(\Delta=0\)来解决,相对运算能快一些。
【题型Ⅱ】求函数\(y=f(x)\)的单调区间或判断单调性
- 类型1:数字系数的函数的单调性的求解或证明
思路方法:转化为数字系数的不等式的求解,求解过程可以借助导函数的图像或者导函数的分子图像或者导函数的组成部分的图像,以形助数,简化求解;
(1).求\(a,b\)的值。
【分析】(1)通过导函数方程和二次函数对称轴方程建立方程组,即可解得a、b,
由于\(f'(x)=6x^2+2ax+b\),且对称轴为\(x=-\cfrac{1}{2}\),
则有\(-\cfrac{a}{6}=-\cfrac{1}{2}\),则\(a=3\),
又由于\(f'(1)=0\),则\(6+2a+b=0\),解得\(b=-12\),
所以\(a=3,b=-12\)。
(2).判断函数的单调性,并求函数的极值。
【解答】数字系数的三次多项式函数求极值,用常规的思路和步骤求解即可。
因为\(f(x)=2x^3+3x^2-12x+1\),\(f'(x)=6x^2+6x-12=6(x^2+x-2)\)
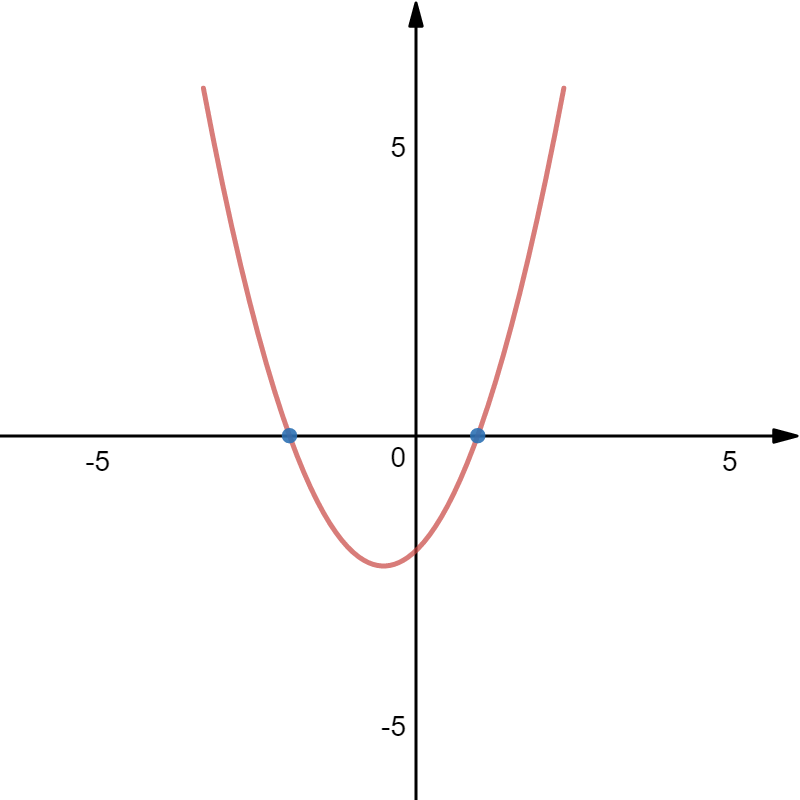
常规的解法这样写道:
令\(f'(x)≥0\),即\(x^2+x-2≥0\),解得\(x≥1\)或\(x≤-2\),
令\(f'(x) ≤0\),即\(x^2+x-2 ≤0\),解得$ -2≤x ≤1$,
有了辅助图像后,我们这些写:
当\(x< -2\)时,\(f'(x)>0\),\(f(x)\)单调递增;
当\(-2<x<1\)时,\(f'(x)<0\),\(f(x)\)单调递减;
当\(x>1\)时,\(f'(x)>0\),\(f(x)\)单调递增;
然后做总结:
所以函数\(f(x)\)在\((-2,1)\)上单调递减,在\((-\infty,-2)\)和\((1,+\infty)\)上单调递增,
当\(x=-2\)时,\(f(x)\)取得极大值,为\(f(-2)=21\),
当\(x=1\)时,\(f(x)\)取得极小值,为\(f(1)=-6\)。
- 类型2:字母系数的函数的单调性的求解
思路方法:转化含参不等式的求解,难点是分类讨论和数形结合
【分析】借助导函数的分子函数的动态图像,即可判断导函数的正负,从而判断原函数的单调性。
【解答】辅助图像
\(f'(x)=2x+\cfrac{2m}{x}-(m+4)=\cfrac{2x^2-(m+4)x+2m}{x}=\cfrac{(x-2)(2x-m)}{x}\),
令\(f'(x)=0\),得到\(x=2\)或\(x=\cfrac{m}{2}>0\),只需要借助分子函数的图像,即可判断导函数的正负,
当\(0<\cfrac{m}{2}<2\)时,即\(0< m <4\)时, \(x\in (0,\cfrac{m}{2})\)时,\(f'(x)>0\),\(f(x)\)单调递增,
\(x\in (\cfrac{m}{2},2)\)时,\(f'(x)<0\),\(f(x)\)单调递减,\(x\in (2,+\infty)\)时,\(f'(x)>0\),\(f(x)\)单调递增,
当\(\cfrac{m}{2}=2\)时,即\(m=4\)时,此时\(f'(x)\ge 0\)恒成立,
当且仅当\(x=2\)时取得等号,故\(f(x)\)在\((0,+\infty)\)上单调递增,
当\(\cfrac{m}{2}>2\)时,即\(m >4\)时, \(x\in (0,2)\)时,\(f'(x) >0\),\(f(x)\)单调递增,
\(x\in (2,\cfrac{m}{2})\)时,\(f'(x) <0\),\(f(x)\)单调递减, \(x\in (\cfrac{m}{2},+\infty)\)时,\(f'(x) >0\),\(f(x)\)单调递增,
综上所述,
当\(0< m <4\)时, \(x\in (0,\cfrac{m}{2})\)时,\(f(x)\)单调递增,
\(x\in (\cfrac{m}{2},2)\)时,\(f(x)\)单调递减,
\(x\in (2,+\infty)\)时,\(f(x)\)单调递增,
当\(m=4\)时,\(f(x)\)在\((0,+\infty)\)上单调递增,
当\(m >4\)时, \(x\in (0,2)\)时,\(f(x)\)单调递增,
\(x\in (2,\cfrac{m}{2})\)时,\(f(x)\)单调递减,
\(x\in (\cfrac{m}{2},+\infty)\)时,\(f(x)\)单调递增,
【题型Ⅲ】已知函数\(y=f(x)\)的单调性,求参数的取值范围
- 类型1:参数包含在函数的系数中
思路方法:若函数\(y=f(x)\)在区间\([a,b]\)单调递增,则\(f'(x)\ge 0\)在区间\([a,b]\)上恒成立,且导函数\(f'(x)\)不恒为\(0\);若函数\(y=f(x)\)在区间\([a,b]\)单调递减,则\(f'(x) \leq 0\)在区间\([a,b]\)上恒成立,且导函数\(f'(x)\)不恒为\(0\);
易错警示:漏掉等号,忘掉验证;
【解答】由函数\(f(x)\)在在区间\((-4,4)\)内单调递增,则\(f'(x)\ge 0\)在区间\((-4,4)\)内恒成立,
又\(f'(x)=(ax+a^2+1)e^{ax}\),注意到\(e^{ax}>0\)恒成立,即有\(ax+a^2+1\ge 0\)在区间\((-4,4)\)内恒成立,
令\(g(x)=ax+a^2+1\)为一次型的函数,故只需要满足\(\left\{\begin{array}{l}{g(-4)\ge 0}\\{g(4)\ge 0}\end{array}\right.\),
即\(\left\{\begin{array}{l}{a^2-4a+1\ge 0}\\{a^2+4a+1\ge 0}\end{array}\right.\),
解得,\(\left\{\begin{array}{l}{a\ge 2+\sqrt{3}或a\leq 2-\sqrt{3}}\\{a\leq -2-\sqrt{3}或a\ge -2+\sqrt{3}}\end{array}\right.\),
即\(a\in (-\infty,-2-\sqrt{3}]\cup[-2+\sqrt{3},2-\sqrt{3}]\cup[2+\sqrt{3},+\infty)\)。
- 类型2:参数包含在给定区间端点处
思路方法:用常规方法求出单调区间,那么给定区间必然是求出的单调区间的子区间,转化为集合的关系求解;
分析:集合法,先用导数的方法求得函数\(f(x)\)的单调递减区间,\(f'(x)=3x^2+3x-6=3(x+2)(x-1)\),
令\(f'(x)<0\),解得\(x\in (-2,1)\),即其单调递减区间为\([-2,1]\),此处必须写成闭区间,否则会丢掉参数的个别取值。
而题设又已知函数在\([a,a+1]\)上单调递减,故\([a,a+1]\subseteq [-2,1]\),即问题转化为集合的包含关系问题了。
此时只需要满足\(\left\{\begin{array}{l}{-2\leqslant a}\\{a+1\leqslant 1}\end{array}\right.\),解得\(-2\leqslant a\leqslant 0\),
故参数\(a\)的取值范围为\([-2,0]\)。
导数法,由题设可知,\(f'(x)=3x^2+3x-6=3(x+2)(x-1)\),由于函数在区间\([a,a+1]\)上单调递减,
则\(f'(x)=3(x+2)(x-1)\leq 0\)在区间\([a,a+1]\)上恒成立,则\(\left\{\begin{array}{l}{f'(a)\leqslant 0}\\{f'(a+1)\leqslant 0}\end{array}\right.\)
即\(\left\{\begin{array}{l}{3(a+2)(a-1)\leqslant 0}\\{3(a+3)a\leqslant 0}\end{array}\right.\),解得\(\left\{\begin{array}{l}{-2\leqslant a\leqslant 1}\\{-3\leqslant a\leqslant 0}\end{array}\right.\),则\(a\in [-2,0]\)。
【题型Ⅳ】函数\(y=f(x)\)存在单调区间,求参数的取值范围
- 类型1:参数包含在函数的系数中
直接法:函数\(y=f(x)\)在区间\([a,b]\)上存在单调递增区间,则\(f'(x)>0\)在区间\([a,b]\)上能成立(或有解);
函数\(y=f(x)\)在区间\([a,b]\)上存在单调递减区间,则\(f'(x)<0\)在区间\([a,b]\)上能成立(或有解);易错警示:多添加了等号;
间接法:不存在单调递增区间,则函数为常函数或单调递减,则恒有\(f'(x)=0\)或\(f'(x)\leq 0\)在区间\([a,b]\)上恒成立;不存在单调递减区间,则函数为常函数或单调递增,则恒有\(f'(x)=0\)或\(f'(x)\ge 0\)在区间\([a,b]\)上恒成立;
交集法:若能容易求得给定函数的单调区间,则求得的该区间和已知的单调区间求交集,即可求得参数的取值范围。
【法1,直接法】:\(g(x)=\cfrac{1}{3}x^3-\cfrac{a}{2}x^2+1+2x\),则\(g'(x)=x^2-ax+2\),
由\(g(x)\)在区间\((-2,-1)\)内存在单调递减区间,得到,
\(g'(x)=x^2-ax+2<0\)在区间\((-2,-1)\)上能成立,
分离参数得到,\(a < x+\cfrac{2}{x}\)在区间\((-2,-1)\)上能成立,
而\(\left(x+\cfrac{2}{x}\right)_{max}=-2\sqrt{2}\),当且仅当\(x=\cfrac{2}{x}\),即\(x=-\sqrt{2}\)时取到等号,
故实数\(a\)的取值范围为\((-\infty,-2\sqrt{2})\)。
注意:若函数\(f(x)\)在区间\((a,b)\)存在单调递减区间,应该得到\(f'(x)<0\)在区间\((a,b)\)有解或能成立,而不是\(f'(x)\leq 0\)在区间\((a,b)\)有解或能成立。
学生认为:函数\(f(x)\)在区间\((a,b)\)存在单调递减区间,应该得到\(f'(x)\leq 0\)在区间\((a,b)\)有解或能成立,这种认识是错误的,这样解释一下啊,
\(f'(x)\leqslant 0\)在区间\((a,b)\)上有解,对应情形一:\(f'(x)<0\)在区间\((a,b)\)上有解;或情形二:\(f'(x)=0\)在区间\((a,b)\)上有解;这两个情形只要有一个满足即可,其中情形一求解结果是区间,而情形二求解结果不是区间,故不符合题意,自然就舍去了。
[反例说明]若\(a=-2\sqrt{2}\),由\(g'(x)=x^2+2\sqrt{2}x+2=(x+\sqrt{2})^2\ge 0\)恒成立,则函数\(g(x)\)只能有单调递增区间,不会存在单调递减区间。
【交集法,正解】函数\(f(x)\)的单调递增区间为\([\cfrac{k}{8},+\infty)\),由题设可知
区间\([\cfrac{k}{8},+\infty)\)和区间\([5,20]\)的交集区间必然不会为空集,否则函数就是空函数了,
则\(\cfrac{k}{8}<20\),解得\(k<160\);即\(k\in(-\infty,160)\);
【导数法,正解】\(f'(x)=8x-k>0\)在区间\([5,20]\)上有解;分离参数得到,\(k<8x\)在区间\([5,20]\)上有解;
即\(k<(8x)_{max}=160\),即\(k\in(-\infty,160)\);
【导数法,错解】\(f'(x)=8x-k\geqslant 0\)在区间\([5,20]\)上有解;分离参数得到,\(k\leqslant 8x\)在区间\([5,20]\)上有解;
即\(k\leqslant (8x)_{max}=160\),即\(k\in(-\infty,160]\);但若\(k=160\)时,单调区间为\([20,+\infty)\),故在\([5,20]\)上没有增区间,故错误;
【法2,间接法】假设函数\(g(x)\)在区间\((-2,-1)\)内不存在单调递减区间,
则函数\(g(x)\)在区间\((-2,-1)\)内为常函数或单调递增,
则恒有\(g'(x)=0\)或\(g'(x)\ge 0\)在区间\((-2,-1)\)内恒成立,
由于\(g'(x)=x^2-ax+2\),显然恒有\(g'(x)=0\)不成立,
故重点探究\(g'(x)\ge 0\)在区间\((-2,-1)\)内恒成立,
\(g'(x)=x^2-ax+2\ge 0\)在区间\((-2,-1)\)内恒成立,分离参数,
得到\(a\ge x+\cfrac{2}{x}(-2< x <-1)\)在区间\((-2,-1)\)内恒成立,
由于\(h(x)=x+\cfrac{2}{x}\)在\((-2,-\sqrt{2}]\)上单调递增,在\([-\sqrt{2},-1)\)上单调递减,
故\(h(x)_{max}=h(-\sqrt{2})=-2\sqrt{2}\),
故函数\(g(x)\)在区间\((-2,-1)\)内不存在单调递减区间时,\(a\ge -2\sqrt{2}\);
即存在单调递减区间时,\(a< -2\sqrt{2}\),即\(a\in (-\infty,-2\sqrt{2})\)。
- 类型2:参数包含在给定区间端点处
思路方法:用常规方法求出单调区间,转化为集合之间的包含关系求解;
分析:由\(f'(x)=3x^2-3=3(x-1)(x+1)\),则可知函数\(f(x)\)的单调递减区间为\([-1,1]\),
又由题设可知,函数\(f(x)=x^3-3x+1\)存在单调递减区间\((a,a+1)\),
则\(f'(x)=3x^2-3<0\)在区间\((a,a+1)\)上恒成立,注意:此处不是能成立;
即有\((a,a+1)\subseteq [-1,1]\),即满足\(\left\{\begin{array}{l}{a<a+1}\\{a\geqslant -1}\\{a+1\leqslant 1}\end{array}\right.\)
解得,\(-1\leqslant a\leqslant 0\),即\(a\in [-1,0]\)。
解后反思:①这类题目应该转化为恒成立而不是能成立类型,否则就不能保证存在这样的单调区间\((a,a+1)\);
②此类题目在命制时要注意,给定的单调区间\(A\)和求解得到的单调区间\(B\)的关系,\(A\subseteq B\),否则解集为空集。
【题型Ⅴ】已知函数的极值点或者最值点,求参数的取值范围
- 类型1:已知函数的极值点或最值点(\(x\)值)
思路方法:①针对参数分类讨论,注意结合题目中的有效信息;
②数形结合法,则函数\(y=f'(x)\)有变号零点,接下来数形结合求解或分离参数求解;
(1)当\(k\leq 0\)时,求函数\(f(x)\)的单调区间;
分析:函数的定义域为\((0,+\infty)\),
\(f'(x)=\cfrac{e^x\cdot x^2-e^x\cdot 2x}{x^4}-k(-\cfrac{2}{x^2}+\cfrac{1}{x})\)
\(=\cfrac{e^x(x-2)}{x^3}-\cfrac{kx(x-2)}{x^3}=\cfrac{(x-2)(e^x-kx)}{x^3}\)
【将上述分式看成三个部分,\(y=x-2\)和\(y=e^x-kx\)和\(y=x^3\),每一个部分的正负必然会影响和决定整体的正负】
注意到\(x^3>0\),当\(k\leq 0\)时,\(e^x-kx>0\),故我们只需要借助\(y=x-2(x>0)\)的图像,就可以判断\(f'(x)\)的正负。
当\(x\in (0,2)\)时,\(f'(x)<0\),\(f(x)\)单调递减;
当\(x\in (2,+\infty)\)时,\(f'(x)>0\),\(f(x)\)单调递增;
故单减区间为\((0,2)\),单增区间为\((2,+\infty)\)。
(2)若函数\(f(x)\)在\((0,2)\)内存在两个极值点,求\(k\)的取值范围。
法1:分类讨论法,
由(1)知,当\(k\leq 0\)时,函数\(f(x)\)在\((0,2)\)内单调递减,
故\(f(x)\)在\((0,2)\)内不存在极值点;
当\(k > 0\)时,设函数\(g(x)=e^x-kx\),\(x\in (0,+\infty)\),
由于\(g'(x)=e^x-k=e^x-e^{lnk}\),
当\(x\in (0,2)\)时,\(e^x \in (1,e^2)\),先考虑\(g'(x)\ge 0\)的情形,故由此找到分点\(k=1\);
当\(0< k \leq 1\)时,\(x\in (0,2)\)时,\(g'(x)=e^x-k >0\),
\(y=g(x)\)单调递增,故\(g(x)_{min}=g(0)=1>0\);
故函数\(f(x)\)在\((0,2)\)内单调递减,故不存在极值点;
当\(k >1\)时,则\(x\in (0,lnk)\)时,\(g'(x)<0\),\(g(x)\)单调递减,
\(x\in (lnk,+\infty)\)时,\(g'(x) >0\),\(g(x)\)单调递增,
所以函数\(y=g(x)\)的最小值为\(g(lnk)=k(1-lnk)\),
那么函数\(f(x)\)在\((0,2)\)内存在两个极值点应该等价于函数\(g(x)\)在\((0,2)\)内存在两个极值点,
函数\(g(x)\)在\((0,2)\)内存在两个极值点当且仅当
\(\left\{\begin{array}{l}{g(0) >0}\\{g(lnk) <0}\\{g(2)>0}\\{0< lnk <2}\end{array}\right.\)
即\(\left\{\begin{array}{l}{e^0-0>0}\\{k(1-lnk) <0}\\{e^2-2k >0}\\{0< lnk <2}\end{array}\right.\)
解得\(e< k <\cfrac{e^2}{2}\);
综上所述,函数\(f(x)\)在\((0,2)\)内存在两个极值点,则\(k\in (e,\cfrac{e^2}{2})\)。
法2:由于函数\(f(x)\)在\((0,2)\)内存在两个极值点,
则函数\(y=f'(x)\)在区间\((0,2)\)内存在两个零点,且为变号零点,
又\(f'(x)=\cfrac{(x-2)(e^x-kx)}{x^3}\),则方程\(f'(x)=\cfrac{(x-2)(e^x-kx)}{x^3}=0\)在\((0,2)\)内有两个不同的实根,
由于\(x\in (0,2)\),即方程\(e^x-kx=0\)在\((0,2)\)内有两个不同的实根,
分离参数,即方程\(k=\cfrac{e^x}{x}\)在\((0,2)\)内有两个不同的实根,
即函数\(y=k\)和函数\(h(x)=\cfrac{e^x}{x}\)的图像在\((0,2)\)内有两个不同的交点,
函数\(y=h(x)\)的限定定义域为\((0,2)\),
由于\(h'(x)=\cfrac{e^x\cdot x-e^x\cdot 1}{x^2}=\cfrac{e^x(x-1)}{x^2}\),
故\(x\in (0,1)\)时,\(h'(x)<0\),\(h(x)\)单调递减,
\(x\in (1,+\infty)\)时,\(h'(x)>0\),\(h(x)\)单调递增,
又由于\(h(1)=e\),根据以上做出函数\(h(x)\)的简图如下,
由图像可知,两个函数的图像要有两个不同的交点,则\(k\in (e,\cfrac{e^2}{2})\)。
故函数\(f(x)\)在\((0,2)\)内存在两个极值点,则\(k\in (e,\cfrac{e^2}{2})\)。
- 类型2:已知函数的极值或最值(\(y\)值)
思路方法:已知函数的极值或最值,常常向讨论函数的单调性方向转化,然后由单调性得到极值或最值,由相等关系得到参数的值;
分析:\(f'(x)=a-\cfrac{1}{x}\),\(x\in (0,e]\),令\(f'(x)=0\),解得\(x=\cfrac{1}{a}\),
结合图像可知,函数在\((0,\cfrac{1}{a}]\)上单调递减,在\([\cfrac{1}{a},e]\)上单调递增,
故\(f(x)_{min}=f(\cfrac{1}{a})=a\times \cfrac{1}{a}-ln\cfrac{1}{a}=1+lna=3\),解得\(lna=2\),即\(a=e^2\),故选\(B\)。
高阶相关引申阅读
接续本节:导数中的题型和破解思路02

 总结梳理导数章节中的常见考查题型和对应的求解思路,以廓清我们的认知。
总结梳理导数章节中的常见考查题型和对应的求解思路,以廓清我们的认知。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号