导数中的题型和破解思路02

前言

相关链接：导数中的题型和破解思路01

知识储备

本节用到的数学思想：分类讨论；转化划归；数形结合；函数与方程；

本节用到的数学方法：导数法，多项式除法，试商法，分组分解法，分离参数法，

恒成立、能成立类命题

题型结构图2

graph TD A[(导数章节题
型总结2)]-->B{已知函数
零点个数求参数
取值范围} A-->C{已知函数
有极值求参数
取值范围} A-->D{已知方程
有n个根求参数
取值范围} A-->E{已知方程
有解或无解求
参数取值范围} A-->F{已知函数
单调或不单调求
参数取值范围}

【题型Ⅵ】已知函数\(f(x)\)的零点个数，求参数的取值范围

• 类型1：给定函数的零点个数

思路方法：常考虑①利用已有的单调性分类讨论确定参数的范围；②不完全分离参数法；③完全分离参数法；

【2017西安模拟】已知函数\(f(x)=kx^2-lnx\)有两个零点，求参数\(k\)的取值范围。

$A.k > \cfrac{e}{2}$ $B.0 < k < \sqrt{e}$ $C.k > \cfrac{\sqrt{2}e}{2}$ $D.0 < k < \cfrac{1}{2e}$

【法1】：数形结合法，定义域为\((0，+\infty)\)，转化为方程\(kx^2=lnx\)有两个不同的实数根，

再转化为函数\(y=kx^2\)与函数\(y=lnx\)的图像有两个不同的交点，

如图设两个函数的图像相切于点为\((x_0，y_0)\)，

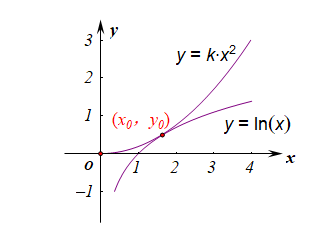
则有关系式\(\begin{cases}2kx_0=\cfrac{1}{x_0}\\kx_0^2=y_0\\y_0=lnx_0\end{cases}\)，

解得\(y_0=\cfrac{1}{2}，x_0=\sqrt{e}\)，即切点为\((\sqrt{e}，\cfrac{1}{2})\)，

再代入函数\(y=kx^2\)，求得此时的\(k=\cfrac{1}{2e}\)，

再结合函数\(y=kx^2\)的系数\(k\)的作用，可得两个函数要有两个不同的交点，

则\(k\in(0，\cfrac{1}{2e})\)。

【法2】：分离参数法，定义域为\((0，+\infty)\)，转化为方程\(kx^2=lnx\)有两个不同的实数根，

再转化为\(k=\cfrac{lnx}{x^2}\)有两个不同的实数根，

再转化为函数\(y=k\)和函数\(y=g(x)=\cfrac{lnx}{x^2}\)的图像有两个不同的交点，

用导数研究函数\(g(x)\)的单调性，\(g'(x)=\cfrac{\cfrac{1}{x}\cdot x^2-lnx\cdot 2x}{(x^2)^2}=\cfrac{1-2lnx}{x^3}\)，

令\(1-2lnx>0\)，得到\(0< x<\sqrt{e}\)，令\(1-2lnx<0\)，得到\(x >\sqrt{e}\)，

即函数\(g(x)\)在区间\((0，\sqrt{e}]\)上单调递增，在\([\sqrt{e}，+\infty)\)上单调递减，

故\(g(x)_{max}=g(\sqrt{e})=\cfrac{1}{2e}\)，

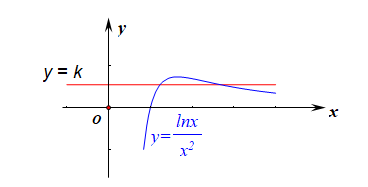
作出函数\(g(x)\)和函数\(y=k\)的简图，由图像可得\(k\)的取值范围是\(k\in(0，\cfrac{1}{2e})\)。

【题型Ⅶ】已知函数\(f(x)\)有极值，求参数的取值范围

• 类型1：含参函数\(f(x)\)有极值，

思路方法：常考虑函数\(y=f'(x)\)有变号零点，再数形结合转化有交点或分离参数转化有解

已知\(|\vec{a}|=2|\vec{b}|\)，\(|\vec{b}| \neq 0\)，且关于\(x\)的函数\(f(x)=\cfrac{1}{3}x^3+\cfrac{1}{2}|\vec{a}|x^2+\vec{a}\cdot \vec{b}x\)在\(R\)上有极值，则\(\vec{a}\)与\(\vec{b}\)的夹角范围是【】

$A.[0，\cfrac{\pi}{6})$ $B.(\cfrac{\pi}{3}，\pi]$ $C.(\cfrac{\pi}{3}，\cfrac{2\pi}{3}]$ $D.(\cfrac{\pi}{6}，\pi]$

分析：函数\(f(x)=\cfrac{1}{3}x^3+\cfrac{1}{2}|\vec{a}|x^2+\vec{a}\cdot \vec{b}x\)在\(R\)上有极值，

其充要条件是其导函数\(y=f'(x)\)存在变号零点，

\(f'(x)=x^2+|\vec{a}|x+\vec{a}\cdot \vec{b}\)，其\(\Delta =|\vec{a}|^2-4\vec{a}\cdot \vec{b}>0\)，

设\(\vec{a}\)与\(\vec{b}\)的夹角为\(\theta\)，

则\(4|\vec{b}|^2-4\times 2|\vec{b}| \cdot |\vec{b}| cos\theta>0\)，

即\(cos\theta<\cfrac{1}{2}\)，由于\(\theta\in [0，\pi]\)，

所以\(\theta \in (\cfrac{\pi}{3}，\pi]\)，故选\(B\)。

• 类型2：含参函数\(f(x)\)有且仅有一个极值

思路方法：常考虑函数\(y=f'(x)\)有且仅有一个变号零点，再数形结合转化为仅有一个交点或分离参数转化有解；

若函数\(f(x)=x^4-ax^3+x^2-2\)有且仅有一个极值点，则实数\(a\)的取值范围是___________。

分析：\(f'(x)=4x^3-3ax^2+2x=x(4x^2-3ax+2)\)，

函数\(f(x)=x^4-ax^3+x^2-2\)有且仅有一个极值点，

其充要条件是因子函数\(h(x)=4x^2-3ax+2\)不存在变号零点，

即\(\Delta=9a^2-32\leq 0\)，解得\(-\cfrac{4\sqrt{2}}{3}\leq a\leq \cfrac{4\sqrt{2}}{3}\)，

即\(a\in [-\cfrac{4\sqrt{2}}{3}，\cfrac{4\sqrt{2}}{3}]\)。

【题型Ⅷ】已知方程\(a=f(x)\)有\(n\)个根，求参数的取值范围

• 类型1：给定或能转化为形如方程\(a=f(x)\)有\(n\)个根

思路方法：需要将所给的题目转化为上述方程有\(n\)个根的形式，难点是利用导数或其他方法做出函数\(f(x)\)的图像，数形结合求解即可。

【已知方程的零点个数，求参数的取值范围】【2019届高三理科函数与方程课时作业第16题改编】已知函数\(f(x)=\left\{\begin{array}{l}{x^2-2x，x\ge 0}\\{-x^2-2x，x<0}\end{array}\right.\)，若方程\(f(x)=a\)恰有\(3\)个不同的解，求\(a\)的取值范围。

分析：转化为函数\(y=f(x)\)和函数\(y=3\)的图像恰有\(3\)个不同的交点，

做出两个函数的图像，由图像可知，要使其有\(3\)个不同的交点，

只需要\(-1< a <1\)，故\(a\in (-1，1)\)。

• 类型2：函数\(g(x)=f(x)-a\)有\(n\)个不同的零点

思路方法：将函数\(g(x)=f(x)-a\)有\(n\)个不同的零点，转化为方程\(a=f(x)\)有\(n\)个不同的根，转化为类型1。

【2019届高三理科数学月考三试题】已知定义在\(R\)上的偶函数\(f(x)\)满足\(f(x+4)=f(x)\)，且当\(0\leq x\leq 2\)时，\(f(x)=min\{-x^2+2x，2-x\}\)，[若函数\(g(x)=f(x)-mx\)恰有两个零点]若方程\(f(x)-mx=0\)恰有两个根，则\(m\)的取值范围是_____________。

分析：先由奇偶性和周期性推知对称性，\(f(-x)=f(x)\)，和\(f(x+4)=f(x)\)，则有\(f(4+x)=f(-x)\)，

则函数\(f(x)\)的对称轴\(x=2\)，

由于当\(0\leq x\leq 2\)时，\(f(x)=min\{-x^2+2x，2-x\}\)，

即当\(0\leq x \leq 2\)时，函数\(f(x)\)的解析式如下，它是做图像的基础。

\(f(x)=\left\{\begin{array}{l}{-x^2+2x，0\leq x\leq 1}\\{2-x，1<x\leq 2}\end{array}\right.\)，

由于方程\(f(x)-mx\)恰有两个根，则函数\(y=f(x)\)与\(y=mx\)恰有两个交点，

做函数\(y=f(x)\)与\(y=mx\)的图像如下图所示，

先看\(x>0\)这一段，记过点\((0，0)\)和\((3，1)\)的直线的斜率为\(k_1\)，则\(k_1=\cfrac{1}{3}\)，

记过点\((0，0)\)且和函数\(y=f(x)=-x^2+2x(0\leq x\leq 1)\)相切的直线的斜率为\(k_2\)，切点为\((x_0，y_0)\)，

则有\(f'(x_0)=-2x_0+2=m①\)；\(y_0=mx_0②\)；\(y_0=-x_0^2+2x_0③\)，

解得\(x_0=0\)，\(y_0=0\)，则切点坐标为\((0，0)\)，斜率\(k_2=2\)，

故在\(x>0\)这一段，两个函数要有两个交点，由图像可得，\(\cfrac{1}{3}<m<2\)，

又由于函数\(f(x)\)定义在\(R\)上，且为偶函数，故在\(x<0\)这一段上，两个函数要有两个交点，\(-2<m<-\cfrac{1}{3}\)，

综上所述，\(m\in (-2，-\cfrac{1}{3})\cup(\cfrac{1}{3}，2)\)。

【题型Ⅸ】已知\(a=f(x)\)有解或无解，求参数的取值范围

• 类型1：给定方程\(a=f(x)\)有解或能转化为方程有解

思路方法：求解行不通时就数形结合；即函数\(y=a\)和函数\(y=f(x)\)的图像有交点，难点：①能顺利转化为本类型；②做函数\(f(x)\)的图像；

函数\(f(x)=x^2\)，\(g(x)=2lnx+a\)有公共点，则\(a\)的取值范围是【】

$A.(e，+\infty)$ $B.(1，+\infty)$ $C.[1，+\infty)$ $D.(-\infty，1)$

法1：在同一个坐标系中，分别作出两个函数的图像，由动函数的图像平移可知\(a\geqslant 1\)，故选\(C\).

法2：转化法，转化为函数\(h(x)=f(x)-g(x)=x^2-2lnx-a\)有零点，分析单调性，令\(h(x)_{min}\leqslant 0\)，故选\(C\).

法3：[重点方法]转化法+分离参数法，转化为\(a=x^2-2lnx\)有解，即函数\(y=a\)和函数\(y=x^2-2lnx\)图像有交点，故选\(C\).

引申：可能还会同时考查整体思想，比如以下的题目；

函数\(f(x)=x^2\)，\(g(x)=2lnx+b^2-b\)有公共点，则\(b\)的取值范围是____________.

函数\(f(x)=x^2\)，\(g(x)=2lnx+a+\cfrac{1}{a}\)有公共点，则\(a\)的取值范围是____________.

• 类型2：给定方程\(a=f(x)\)无解或能转化为方程无解

思路方法：求解行不通时就数形结合；即函数\(y=a\)和函数\(y=f(x)\)的图像无交点，难点：①能顺利转化为本类型；②做函数\(f(x)\)的图像；

方程\(x^2-2lnx-a=0\)无解，则\(a\)的取值范围是【】

$A.(e，+\infty)$ $B.(1，+\infty)$ $C.[1，+\infty)$ $D.(-\infty，1)$

法1：在同一个坐标系中，分别作出两个函数的图像，由动函数的图像平移可知\(a\geqslant 1\)，故选\(D\).

法2：转化法，转化为函数\(h(x)=x^2-2lnx-a\)无零点，分析单调性，令\(h(x)_{min}> 0\)，故选\(D\).

法3：[重点方法]转化法+分离参数法，转化为\(a=x^2-2lnx\)无解，即函数\(y=a\)和函数\(y=x^2-2lnx\)图像无交点，故选\(D\).

引申：可能还会同时考查整体思想，比如以下的题目；

函数\(f(x)=x^2\)，\(g(x)=2lnx+b^2-b\)无公共点，则\(b\)的取值范围是____________.

函数\(f(x)=x^2\)，\(g(x)=2lnx+a+\cfrac{1}{a}\)无公共点，则\(a\)的取值范围是____________.

【题型Ⅹ】函数\(y=f(x)\)在区间\((a，b)\)上单调或不单调，求参数的取值范围

• 类型1：函数\(y=f(x)\)在区间\((a，b)\)上单调

思路方法：①分类讨论，单调递增时，\(f'(x)\ge 0\)恒成立；单调递减时，\(f'(x)\leq 0\)恒成立；结果求并集；

②直接法，由于函数单调，则\(y=f'(x)\)无零点，或有不变号零点，再转化为方程\(f'(x)=0\)无解或有切点解的形式。

函数\(f(x)=\cfrac{1}{3}x^3-x^2+ax-5\)在区间\([-1，2]\)上单调，则实数\(a\)的取值范围是_________。

法1：分类讨论法，\(f'(x)=x^2-2x+a\)，

若函数\(f(x)\)在\([-1，2]\)上单增，则\(f'(x)=x^2-2x+a\ge 0\)恒成立，

分离参数得到\(a\ge -x^2+2x\)恒成立，

在\([-1，2]\)上求得函数\(f(x)_{max}=1\)，故\(a\ge 1\)；

若函数\(f(x)\)在\([-1，2]\)上单减，则\(f'(x)=x^2-2x+a\leq 0\)恒成立，

分离参数得到\(a\leq -x^2+2x\)恒成立，

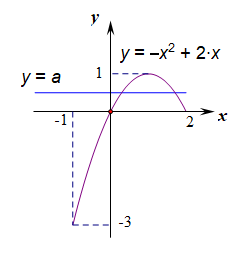
在\([-1，2]\)上求得函数\(f(x)_{min}=-3\)，故\(a\leq -3\)；

故当\(a\in (-\infty，-3]\cup[1，+\infty)\)时，函数\(f(x)\)在区间\([-1，2]\)上单调。

法2：直接法，由于函数\(f(x)=\cfrac{1}{3}x^3-x^2+ax-5\)在区间\([-1，2]\)上单调，

则函数\(y=f'(x)\)在区间\([1，2]\)上无零点，

即方程\(f'(x)=x^2-2x+a=0\)在区间\([1，2]\)上无解，

即方程\(a=-x^2+2x\)在区间\([1，2]\)上无解，

由图像可知，\(f'(x)\)的值域为\([-3，1]\)，

故方程\(f'(x)=0\)无解时得到，\(a < -3\)或\(a >1\)，

由于上述的转化是不等价的，以下检验端点值是否满足题意。

当\(a=-3\)时，\(f'(x)=x^2-2x-3=(x+1)(x-3)\)，此时若\(x\in [-1，2]\)，

则有\(f'(x)\leq 0\)恒成立，故函数\(f(x)\)在区间\([-1，2]\)上单调递减，

符合题意，添加\(a=-3\)；

当\(a=1\)时，\(f'(x)=x^2-2x+1=(x-1)^2\)，此时若\(x\in [-1，2]\)，

则有\(f'(x)\ge 0\)恒成立，故函数\(f(x)\)在区间\([-1，2]\)上单调递增，

符合题意，添加\(a=1\)；

综上所述，函数\(f(x)=\cfrac{1}{3}x^3-x^2+ax-5\)在区间\([-1，2]\)上单调，

则实数\(a\)的取值范围是\(a\in (-\infty，-3]\cup[1，+\infty)\)。

• 类型2：函数\(y=f(x)\)在区间\((a，b)\)上不单调

思路方法：①补集法，先求在区间\((a，b)\)上单调时的参数范围，再求其补集

②直接法，函数不单调，则\(y=f'(x)\)有变号零点，则方程\(f'(x)=0\)有解，且为变号解的形式；

函数\(f(x)=\cfrac{1}{3}x^3-x^2+ax-5\)在区间\([-1，2]\)上不单调，则实数\(a\)的取值范围是_________。

法1：间接法，从反面入手，利用补集思想，\(f'(x)=x^2-2x+a\)，

若函数\(f(x)\)在\([-1，2]\)上单增，则\(f'(x)=x^2-2x+a\ge 0\)恒成立，

分离参数得到\(a\ge -x^2+2x\)恒成立，

在\([-1，2]\)上求得函数\(f(x)_{max}=1\)，故\(a\ge 1\)；

若函数\(f(x)\)在\([-1，2]\)上单减，则\(f'(x)=x^2-2x+a\leq 0\)恒成立，

分离参数得到\(a\leq -x^2+2x\)恒成立，

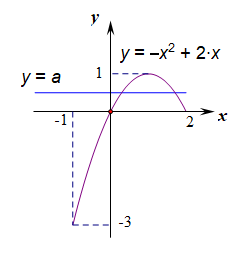
在\([-1，2]\)上求得函数\(f(x)_{min}=-3\)，故\(a\leq -3\)；

则当\(a\leqslant -3\)或\(a\geqslant 1\)时，函数函数\(f(x)\)在\([-1，2]\)上单调，

故取其补集，当\(-3< a <1\)时，函数\(f(x)\)在区间\([-1，2]\)上不单调。

法2：从正面入手分析，直接法，由题可知\(f(x)\)不单调，则导函数\(y=f'(x)\) 在开区间\((-1,2)\)内注意此处必须是开区间\((-1,2)\)而不能是闭区间\([-1,2]\)，如果是闭区间，且导函数刚好只过点\(x=-1\)，在\((-1,2]\)上为正，则此时原函数是单调递增的\(\quad\)至少有一个变号零点，

当只有一个变号零点时，由\(f'(-1)\cdot f'(2)< 0\)可得，\(-3< a< 0\)；

当有两个变号零点时，由\(\begin{cases}f'(-1)\geqslant0\\f'(2)\geqslant0\\\Delta >0\end{cases}\)，解得\(0\leqslant a<1\)；

综上所述，实数\(a\)的取值范围是\((-3，1)\)。

解后反思：其实应该转化为导函数\(y=f'(x)\)在区间\((-1，2)\)上至少有一个变号零点，不应该包含端点值，如果是仅仅过一个端点值，或者刚好过两个端点值时，函数都是单调的。

法3：(转化为方程有解类型求解)由法2可知，导函数\(y=f'(x)\)在区间\([-1，2]\)上至少有一个变号零点，

即方程\(f'(x)=0\)至少有一个解，故\(a=-x^2+2x\)在\([-1，2]\)上至少有一个解，

到此转化为方程有解类型，需要求函数的值域。

需要求出函数\(y=-x^2+2x，x\in [-1，2]\)上的值域\([-3，1]\)，

由于上述的转化过程不是等价的等价的转化应该是方程\(f'(x)=0\)在区间\([1,2]\)上至少有一个解，且解不能是切点解必须是穿根解，且还不能是过区间端点的穿根解；\(\quad\)，故需要检验。

当\(a=-3\)时，\(f'(x)=x^2-2x-3=(x+1)(x-3)\)，此时若\(x\in [-1，2]\)，

则有\(f'(x)\leq 0\)恒成立，故函数\(f(x)\)在区间\([-1，2]\)上单调递减，

不符合题意，舍去；

当\(a=1\)时，\(f'(x)=x^2-2x+1=(x-1)^2\)，此时若\(x\in [-1，2]\)，

则有\(f'(x)\ge 0\)恒成立，故函数\(f(x)\)在区间\([-1，2]\)上单调递增，

不符合题意，舍去；故实数\(a\)的取值范围是\((-3，1)\)。

解后反思：若能直接转化为导函数\(y=f'(x)\)在区间\((-1，2)\)上至少有一个变号零点，就省却了验证了。

【2020\(\cdot\)成都模拟】已知函数 \(f(x)=-\cfrac{1}{2}x^{2}+4x-3\ln x\) 在区间\([t, t+1]\)上不单调，则\(t\) 的取值范围是_________.

解析：由题意知 \(f'(x)=-x+4-\cfrac{3}{x}=-\cfrac{(x-1)(x-3)}{x}\)，

由\(f'(x)=0\) 得函数 \(f(x)\)的两个极值点为\(1\)和\(3\)，

则只要这两个极值点有一个在区间\((t, t+1)\)内，函数 \(f(x)\)在区间 \([t, t+1]\) 上就不单调,

所以\(1\in(t, t+1)\) 或 \(3\in(t, t+1)\)

即\(\left\{\begin{array}{l}{t<1},\\{t+1>1}\end{array}\right.\)或\(\left\{\begin{array}{l}{t<3}\\{t+1>3}\end{array}\right.\)

解得\(0<t<1\) 或 \(2<t<3\)，故填写 \((0,1)\cup(2,3)\)；

【2018宝鸡市高三数学第一次质量检测第21题】已知函数\(f(x)=\cfrac{x}{lnx}+ax，x>1\)；

(1).若函数\(f(x)\)在区间\((1，+\infty)\)上单调递减，求实数\(a\)的取值范围；

分析：切入点，函数\(f(x)\)在某区间单调递减，则导函数\(f'(x)\leq 0\)在此区间恒成立，(本来还需要验证\(a\)的取值不能使原函数成为常函数，此题中口算验证就可以)。

\(f'(x)=\cfrac{lnx-1}{ln^2x}+a\)，由题可知\(f'(x)=\cfrac{lnx-1}{ln^2x}+a\leq 0\)在区间\((1，+\infty)\)上恒成立，

分离参数得到，\(a\leq \cfrac{1-lnx}{ln^2x}=\cfrac{1}{ln^2x}-\cfrac{1}{lnx}\)，

令\(g(x)=\cfrac{1}{ln^2x}-\cfrac{1}{lnx}\)，此时只需要求出\(g(x)_{min}\)即可。

为了求得\(g(x)_{min}\)，我们可以考虑导数法，不过如果能注意到函数的结构特征，还可以有其他的选择。

思路1(二次函数法)：令\(lnx=t\)，则由于\(x>1\)，得到\(lnx=t>0\)，这样\(g(x)=\cfrac{1}{ln^2x}-\cfrac{1}{lnx}=(\cfrac{1}{t})^2-\cfrac{1}{t}=h(t)\)

\(h(t)=(\cfrac{1}{t}-\cfrac{1}{2})^2-\cfrac{1}{4}\)，

当\(\cfrac{1}{t}=\cfrac{1}{2}\)，即\(t=2=lnx\)，即\(x=e^2>1\)时，\(h(t)_{min}=g(x)_{min}=-\cfrac{1}{4}\)，

故实数\(a\)的取值范围为\(a\leq -\cfrac{1}{4}\)，即\(a\in(-\infty，-\cfrac{1}{4}]\)。

思路2(导数法)：令\(g(x)=\cfrac{1-lnx}{ln^2x}\)，则\(g'(x)=\cfrac{(1-lnx)'\cdot ln^2x-(1-lnx)\cdot 2lnx\cdot \cfrac{1}{x}}{(ln^2x)^2}\)

\(g'(x)=\cfrac{-\cfrac{1}{x}\cdot ln^2x-(1-lnx)\cdot \cfrac{2}{x}\cdot lnx}{ln^4x}=\cfrac{-\cfrac{1}{x}\cdot lnx-\cfrac{2}{x}+\cfrac{2}{x}\cdot lnx}{ln^3x}\)

\(g'(x)=\cfrac{\cfrac{1}{x}\cdot lnx-\cfrac{2}{x}}{ln^3x}=\cfrac{\cfrac{1}{x}(lnx-2)}{ln^3x}\)

由于\(x>1\)，故\(g'(x)\)的表达式中的因子\(\cfrac{1}{x}>0\)和分母\(ln^3x>0\)，故我们到时候解不等式，就可以只解\(lnx-2>0(lnx-2<0)\)，

当然如果我们能借助导函数的部分\(y=lnx-2\)的图像，就可以直接读出解集来，这也就是数形结合思想给我们的启示。

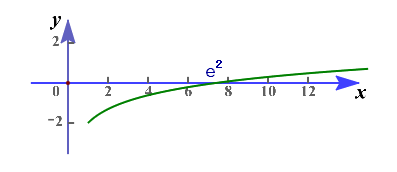
由图可知当\(x\in(1，e^2)\)时，\(lnx-2<0\)，即\(g'(x)<0\)；当\(x>e^2\)时，\(lnx-2>0\)，即\(g'(x)>0\)；

故\(g'(x)\)在\((1，e^2]\)上单调递减，在\([e^2，+\infty)\)上单调递增；

故\(g(x)_{min}=g(e^2)=\cfrac{1-lne^2}{(lne^2)^2}=\cfrac{1-2}{2^2}=-\cfrac{1}{4}\)，即\(a\leq -\cfrac{1}{4}\)。

反思：①、求函数\(g(x)\)的最小值时，这两个思路都是比较常用的，不过很明显二次函数法要简单一些。尽可能的防止不好的思维定式，不要一想到求最值就求导，当然求导是一种选择，不过是没有其他办法时的备选方法。

②、\(ln^2x\)的求导是复合函数的求导，容易出错。\((ln^2x)'=2lnx\cdot (lnx)'=2lnx\cdot \cfrac{1}{x}\).

③、其他内容请参阅【恒成立等三类命题赏析】 【恒成立命题习题】

(2).若方程\((2x-m)lnx+x=0\)在区间\((1，e]\)上有两个不相等实根，求实数\(m\)的取值范围；

分析：这类题目往往需要分离参数，得到形如\(m=g(x)\)的形式，然后转化为函数有两个交点的问题，从而数形结合求解；

由题目分离参数，\(2x\cdot lnx-mlnx+x=0\)，变形整理为\(m=\cfrac{2xlnx+x}{lnx}=\cfrac{x}{lnx}+2x\)，

令\(h(x)=\cfrac{x}{lnx}+2x，x\in(1，e]\)，则往下的思路是想办法在同一个坐标系中做函数\(h(x)\)和函数\(y=m\)的图像，其中做函数\(h(x)\)的图像一般要用到导数方法，主要是涉及的函数比较复杂，一般方法不能处理。

则\(h'(x)=2+\cfrac{lnx-1}{ln^2x}=\cfrac{2ln^2x+lnx-1}{ln^2x}=\cfrac{(lnx+1)(2lnx-1)}{ln^2x}\)，由于\(x>1\)，则\(lnx+1>0\)且\(ln^2x>0\)，故我们只需要解不等式\(2lnx-1>0(2lnx-1<0)\)就可以求得单调区间；在这里我们自然还可以借助图像，做出导函数的部分函数的图像如右图，

由图可知，\(x\in (1，\sqrt{e}]\)时，\(2lnx-1<0\)，\(h'(x)<0\)，函数\(h(x)\)单调递减；\(x\in [\sqrt{e}，e]\)时，\(2lnx-1>0\)，\(h'(x)>0\)，函数\(h(x)\)单调递增；

又\(h(\sqrt{e})=2\sqrt{e}+\cfrac{\sqrt{e}}{ln\sqrt{e}}=4\sqrt{e}\)；\(h(e)=2e+\cfrac{e}{lne}=3e\)，其中\(x=1\)是函数\(h(x)\)的渐近线，如右图所示，

由图可知，实数\(m\)的取值范围为\(m\in (4\sqrt{e}，e]\)。

解后反思：①、函数\(h(x)\)的单调性的求法(一般题目复杂时常常首选导数法)；

②、注意函数图像的作图细节；

③、如果题目变成\(m=g(x)\)有解，则\(m\)的取值范围就是\(g(x)\)的值域，看看刚才的图形，这一点不需要我多解释了吧。

④、如果题目变成方程\(m=g(x)\)有\(n\)个解，那更需要数形结合来处理了；因为用代数的方法求解，只能处理简单的方程的情形，复杂一些的只能交给图形来直观观察