二元函数 $f(x,y)$

前言

变形策略

• 均值不等式，出现 \(a+b\) 或 \(ab\) ，可以将其中一个用另一个代换，整理为关于整体单个元 \(ab\) 或者整体单个元 \(a+b\) 的不等式求解；

• 变量集中，若等式或不等式为齐次式，则利用 \(\cfrac{a}{b}=t\) 变量个数，或者已知等式为 \(g(a,b)=0\) 的形式[如 \(2a+3b=2\)]，则常利用 \(b=f(a)\) 的形式[如 \(b=\cfrac{2-2a}{3}\)]减少变量个数；

• 数形结合，转化为关于形的几何意义求解，比如距离型，斜率型等；

典例剖析

已知\(x>0\)，\(y>0\)，若\(\cfrac{2y}{x}+\cfrac{8x}{y}>m^2+2m\)恒成立，则实数\(m\)的取值范围是多少？

分析：由恒成立命题可知，需要\((\cfrac{2y}{x}+\cfrac{8x}{y})_{min}>m^2+2m\)，

\(\cfrac{2y}{x}+\cfrac{8x}{y}\ge 2\sqrt{\cfrac{2y}{x}\cdot \cfrac{8x}{y}}=8\)，当且仅当\(y=2x\)时取到等号。

故\(m^2+2m-8<0\)，解得\(-4<m<2\)。

设二次函数\(f(x)=ax^2+bx+c\)的导函数是\(f'(x)\)，若对\(\forall x\in R\)，不等式\(f(x)\ge f'(x)\)恒成立，则\(\cfrac{b^2}{a^2+2c^2}\)的最大值是____________.

分析：由\(\forall x\in R\)，不等式\(f(x)\ge f'(x)\)恒成立，得到\(b^2 \leq 4ac-4a^2\)，(由于\(4ac-4a^2>0\)，即\(\cfrac{c}{a}=t>1\))

故有\(\cfrac{b^2}{a^2+2c^2} \leq \cfrac{4ac-4a^2}{a^2+2c^2}\)，由题目可知\(a>0\)，

给分子分母同除以\(a^2\)，得到 \(\cfrac{4ac-4a^2}{a^2+2c^2}=\cfrac{4\times\cfrac{c}{a}-4}{1+2\times(\cfrac{c}{a})^2}\)

做代换，令\(\cfrac{c}{a}=t\)，则 \(\cfrac{4ac-4a^2}{a^2+2c^2}=\cfrac{4t-4}{2t^2+1}\)，

关于此式的变换比较难，我们转而求\(\cfrac{2t^2+1}{4t-4}\)的最小值。

而\(\cfrac{2t^2+1}{4t-4}=\cfrac{2(t-1)^2+4(t-1)+3}{4(t-1)}=\cfrac{t-1}{2}+\cfrac{3}{4(t-1)}+1 \ge 2\sqrt{\cfrac{3}{8}}+1=\cfrac{\sqrt{6}+2}{2}\)

故\([\cfrac{4t-4}{2t^2+1}]_{max}=\cfrac{2}{\sqrt{6}+2}=\sqrt{6}-2\)。则\(\cfrac{b^2}{a^2+2c^2}\)的最大值是\(\sqrt{6}-2\).

【值域问题，斜率型】求函数\(y=f(x)=\cfrac{sinx-1}{cosx+2}\)的值域；

法1：反解法+辅助角公式，先反解得到\(sinx-y\cdot cosx=1+2y\)，

即\(\sqrt{y^2+1}\cdot sin(x+\phi)=2y+1\)，即\(sin(x+\phi)=\cfrac{2y+1}{\sqrt{y^2+1}}\)，

故有\(|\cfrac{2y+1}{\sqrt{y^2+1}}|\leq 1\)，两边平方得到\((2y+1)^2\leq y^2+1\) ，

解得$ -\cfrac{4}{3}\leq y\leq 0$。

法2：数形结合，此题目可以看成动点\((cosx，sinx)\)到定点\((-2，1)\)的连线的斜率的取值范围，

而动点\((cosx，sinx)\)的轨迹是单位圆，作出图像如右，

可以得到连线斜率\(y_{max}=0\)，而\(y_{min}\)应该是定点与图中的切点\((x_0，y_0)\)的连线的斜率。

以下求切点\((x_0，y_0)\)。

由\(\begin{cases} \cfrac{y_0-1}{x_0+2}\cdot \cfrac{y_0}{x_0}=-1 ①\\x_0^2+y_0^2=1 ②\end{cases}\)，

②代入①解得\(y_0-2x_0=1\)，联立②式，

从而解得\(x_0=-\cfrac{4}{5}或x_0=0(舍去)\)，\(y_0=-\cfrac{3}{5}\)，

代入求得另一个相切的斜率\(k=y_{min}=\cfrac{1+\cfrac{3}{5}}{-2+\cfrac{4}{5}}=-\cfrac{4}{3}\)，

故$ -\cfrac{4}{3}\leq y\leq 0$。

【2019届高三理科数学二轮用题】已知函数\(f(x)=-x^3+mx+2\)，\(g(x)=2x^2-nx\)，且曲线\(y=f(x)\)在点\((2，f(2))\)处的切线于曲线\(y=g(x)\)在点\((1，g(1))\)处的切线平行，则\(\sqrt{m^2+n^2}\)的最小值为_______。

法1：由已知条件可知，\(m+n=16\)，若从数的角度入手分析，则\(m=16-n\)，

转化为先求\(m^2+n^2=(16-n)^2+n^2=2n^2-32n+16^2=2(n-8)^2+128\)，

故\((m^2+n^2)_{min}=128\)，故所求最小值为\(\sqrt{128}=8\sqrt{2}\)。

法2：由已知条件可知，\(m+n=16\)，若从形的角度入手分析，建立如图所示的坐标系，

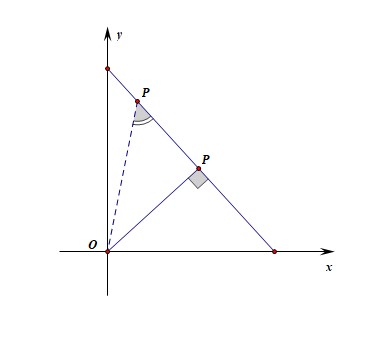
可知，\(m+n=16\)表示一条直线，\(\sqrt{m^2+n^2}=\sqrt{(m-0)^2+(n-0)^2}\)表示定点\((0，0)\)与动点\((m，n)\)的距离，

故所求的最小距离为\(8\sqrt{2}\)。

【2016第三次全国大联考地16题】若不等式\(2x^2+(1-a)y^2\ge (3+a)xy(x>0，y>0)\)恒成立，求实数\(a\)的最大值。

【法1】：分离参数+构造函数，由题目可得\(a\leq \cfrac{2x^2+y^2-3xy}{y^2+xy}\)，

令\(f(x,y)= \cfrac{2x^2+y^2-3xy}{y^2+xy}\xlongequal[关于x，y的二次齐次式]{分子分母同除以y^2}\cfrac{2(\cfrac{x}{y})^2-3\cfrac{x}{y}+1}{1+\cfrac{x}{y}}\\\xlongequal[令\cfrac{x}{y}=t>0]{二元变一元}g(t)=\cfrac{2t^2-3t+1}{t+1}=2(t+1)+\cfrac{6}{t+1}-7\ge 2\sqrt{12}-7=4\sqrt{3}-7\)

当且仅当\(t=\sqrt{3}-1\)时取到等号。

故有\(a\leq 4\sqrt{3}-7\)，所以\(a_{max}=4\sqrt{3}-7\)。

【法2】：二元变一元，两边同除以\(y^2\)，得到\(2(\cfrac{x}{y})^2-(a+3)(\cfrac{x}{y})+(1-a)\ge 0\)，

令\(\cfrac{x}{y}=t>0\)，即\(2t^2-(a+3)t+(1-a)\ge 0\)对任意\(t>0\)恒成立，

令\(g(t)=2t^2-(a+3)t+(1-a)\) ，则分以下两种情形：

\(1^。\) \(\Delta=a^2+14a+1\leq 0\)，

解得\(-4\sqrt{3}-7\leq a \leq 4\sqrt{3}-7\)；

\(2^。\) \(\begin{cases}\Delta >0\\\cfrac{a+3}{2\cdot2}<0\\g(0)=1-a\ge 0 \end{cases}\)，

解得\(a<-4\sqrt{3}-7\)；

综上可知，\(a\leq 4\sqrt{3}-7\)，故\(a_{max}=4\sqrt{3}-7\)。

【2018河南郑州一模】若对于任意的正整数\(x\)，\(y\)都有\((2x-\cfrac{y}{e})\cdot ln\cfrac{y}{x}\leq \cfrac{x}{me}\)成立，则实数\(m\)的取值范围是【】

$A.(\cfrac{1}{e}，1)$ $B.(\cfrac{1}{e^2}，1]$ $C.(\cfrac{1}{e^2}，e]$ $D.(0，\cfrac{1}{e}]$

分析：先将给定的式子通分变形为\(\cfrac{2ex-y}{e}\cdot ln\cfrac{y}{x}\leq \cfrac{x}{me}\)，

再次变形为\((2e-\cfrac{y}{x})\cdot ln\cfrac{y}{x}\leq \cfrac{1}{m}\)，

令\(\cfrac{y}{x}=t>0\)，则不等式变形为\((2e-t)\cdot lnt\leq \cfrac{1}{m}\)，

令\(h(t)=(2e-t)\cdot lnt\)，则需要求\(h(t)_{max}\)；

\(h'(x)=(-1)lnt+(2e-t)\cdot \cfrac{1}{t}=\cfrac{-t(lnt+1)+2e}{t}\)，

先用观察法或经验找到导函数的分子的零点\(t=e\)，

当\(t\in (0，e)\)时，\(h'(t)>0\)，\(h(t)\)单调递增，

当\(t\in (e，+\infty)\)时，\(h'(t)<0\)，\(h(t)\)单调递减，

故\(h(t)_{max}=h(e)=e\)，即\(\cfrac{1}{m}\ge e\)，

解得\(0<m\leq \cfrac{1}{e}\)；故选\(D\)。

【二元函数】若存在两个正实数\(x，y\)，使得等式\(3x+a(2y-4ex)\cdot(lny-lnx)=0\)成立，其中\(e\)为自然对数的底数，则\(a\)的取值范围是__________。

分析：由于\(x\neq 0\)，故两边同时除以\(x\)，二元变一元，变量集中，

得到\(3+a(2\cdot \cfrac{y}{x}-4e)\cdot ln\cfrac{y}{x}=0\)，令\(\cfrac{y}{x}=t>0\)，

则\(3+a(2t-4e)\cdot lnt=0\)，即\(2a(t-2e)\cdot lnt=-3\)，

由于\(a\neq 0\)，则上式变形为\((t-2e)\cdot lnt=-\cfrac{3}{2a}\)，

即存在正数\(t\)，使得方程\((t-2e)\cdot lnt=-\cfrac{3}{2a}\)有解，

令\(g(t)=(t-2e)\cdot lnt\)，则 \(g'(t)=\ln t+1-\cfrac{2e}{t}\)，显然 \(g'(t)\) 是增函数，

\(g'(e)=\ln e+1-\cfrac{2e}{e}=1+1-2=0\)，

当 \(t>e\) 时 \(g'(t)>0\)，当 \(0<t<e\) 时 \(g'(t)<0\)

即当 \(t=e\) 时， 函数 \(g(t)\) 取得极小值为 \(g(e)=(e-2e)\ln e=-e\)，

即 \(g(t)\geqslant g(e)=-e\)，

若\((t-2e)\cdot lnt=-\cfrac{3}{2a}\)有解，

则 \(-\cfrac{3}{2a}\geqslant -e\)， 即 \(\cfrac{3}{2a}\leqslant e\)，

则解得 \(a<0\) 或 \(a\geqslant \cfrac{3}{2a}\)，

故实数 \(a\) 的取值范围是 \((-\infty, 0)\cup[\cfrac{3}{2e},+\infty)\) .

【2022届高三数学三轮模拟冲刺用题】【对应练习】若存在两个正实数\(x\)，\(y\)，使得等式 \(x\)\((2+\ln x)\)\(=\)\(x\ln y\)\(-\)\(ay\) 成立，则实数 \(a\) 的取值范围是 【\(\qquad\)】

$A.(0,\cfrac{1}{e^2})$ $B.(-\infty,\cfrac{1}{e^2}]$ $C.(0,\cfrac{1}{e^3})$ $D.(-\infty,\cfrac{1}{e^3}]$

解析：审题中我们发现，本题目就是二元方程有解类型的，故我们想到能不能通过变量集中，将二元方程转化为一元方程问题；

两边同时除以 \(x\)，变形得到 \(2+\ln x=\ln y-a\cdot \cfrac{y}{x}\)，

再整理为 \(a\cdot \cfrac{y}{x}=\ln\cfrac{y}{x}-2\)，接下来换元，令 \(\cfrac{y}{x}=t\)，则 \(t>0\)，

即上式变换为 \(at=\ln t-2\)，分离参数得到，\(a=\cfrac{\ln t-2}{t}\) 在 \(t\in (0,+\infty)\) 上有解，

令 \(g(x)=\cfrac{\ln t-2}{t}\) ，则接下来就是求解函数 \(g(x)\) 的值域问题了。

用导数法可以求得[此处详细过程略]，\(g(x)_{\max}=\cfrac{1}{e^3}\)，则 \(a\leqslant \cfrac{1}{e^3}\)，故选 \(D\) .

已知实数\(a、b\)满足条件\(\left\{\begin{array}{l}{a+b-2\ge 0}\\{b-a-1\leq 0}\\{a\leq 1}\end{array}\right.\)，求\(\cfrac{a+2b}{2a+b}\)的取值范围。

【法1】转化为斜率型，

思路如下：由于所求值函数为分式形式的关于\(a、b\)的二次齐次式，

故可以转化为\(\cfrac{a+2b}{2a+b}=\cfrac{1+2\cdot \cfrac{b}{a}}{2+\cfrac{b}{a}}\)\(=2-\cfrac{3}{2+k}=f(k)\)，

其中\(k=\cfrac{b}{a}\)

这样先由可行域求得\(k=\cfrac{b}{a}\in [1，3]\)

函数\(f(k)\)在区间\([1，3]\)上单调递增，

然后用单调性，求得\(\cfrac{a+2b}{2a+b}\in [1，\cfrac{7}{5}]\)

【法2】换元法，令\(a+2b=n\)，\(2a+b=m\)，

联立解以\(a、b\)为元的方程组，得到

\(a=\cfrac{2m-n}{3}\)，\(b=\cfrac{2n-m}{3}\)，

代入原不等式组，可将原约束条件转化为关于\(m 、n\)的不等式组，

即已知\(m 、n\)满足条件\(\left\{\begin{array}{l}{m+n-6\ge 0}\\{n-m-1\leq 0}\\{2m-n-3\leq 0}\end{array}\right.\)，求\(\cfrac{n}{m}\)的取值范围。

利用数形结合思想可得，\(\cfrac{a+2b}{2a+b}=\cfrac{n}{m}\in [1，\cfrac{7}{5}]\)。图像

【2018届凤翔中学高三文科冲刺模拟第10套第12题】已知函数\(f(x)=ln\cfrac{x}{2}+\cfrac{1}{2}\)，\(g(x)=e^{x-2}\)，若\(g(m)=f(n)\)成立， 则\(n-m\)的最小值为【】

$A.1-ln2$ $B.ln2$ $C.2\sqrt{e}-3$ $D.e^2-3$

分析：不妨设\(g(m)=f(n)=t\)，则\(e^{m-2}=ln\cfrac{n}{2}+\cfrac{1}{2}=t(t>0)\)，

(编者注：此处引入第三方变量\(t\)，可以将\(m、n\)用含有\(t\)的表达式来刻画，则二元函数就此转化为了一元函数，我们就可以用导数求其最值了)

则\(m-2=lnt\)，\(m=2+lnt\)；\(ln\cfrac{n}{2}=t-\cfrac{1}{2}\)，则\(n=2e^{t-\frac{1}{2}}\)；

故\(n-m=2e^{t-\frac{1}{2}}-2-lnt(t>0)\) ，

令\(h(t)=2e^{t-\frac{1}{2}}-2-lnt(t>0)\)，\(h'(t)=2e^{t-\frac{1}{2}}-\cfrac{1}{t}\)，(增+增=增)

易知\(h'(t)\)在\((0，+\infty)\)上单调递增，且\(h(\cfrac{1}{2})=0\)；

当\(t>\cfrac{1}{2}\)时，\(h'(t)>0\)，当\(0<t<\cfrac{1}{2}\)时，\(h'(t)<0\)，

即当\(t=\cfrac{1}{2}\)时，\(h(t)\)取得极小值也是最小值，

\(h(t)_{min}=h(\cfrac{1}{2})=2e^{\frac{1}{2}-\frac{1}{2}}-2-ln\cfrac{1}{2}=ln2\)，故选\(B\).

已知函数\(f(x)=ax-1-lnx(a\in R)\)

(1)讨论函数\(f(x)\)的单调性。

(2)当\(x>y>e-1\)时，证明不等式\(e^x\cdot ln(1+y)>e^y\cdot ln(1+x)\)

分析：(1)定义域为\((0，+\infty)\)，又\(f'(x)=a-\cfrac{1}{x}=\cfrac{ax-1}{x}\)，

由于分母为正，故只针对分子\(ax-1\)分类讨论，

当\(a\leq 0\)时，\(ax-1<0\)，即\(f'(x)<0\)，故在\((0，+\infty)\)上单调递减；

当\(a>0\)时，令\(ax-1=0\)，得到\(x=\cfrac{1}{a}\)，

故在\((0，\cfrac{1}{a})\)上单调递减，在\((\cfrac{1}{a}，+\infty)\)上单调递增。

(2)将欲证明结论

\(e^x\cdot ln(1+y)>e^y\cdot ln(1+x)\)变形为\(\cfrac{ln(1+y)}{e^y}>\cfrac{ln(1+x)}{e^x}\)，

题目转化为由\(x>y>e-1\)时，证明\(\cfrac{ln(1+y)}{e^y}>\cfrac{ln(1+x)}{e^x}\)，

故我们构造函数\(g(x)=\cfrac{ln(1+x)}{e^x}\)，

这样命题转化为当\(x>y>e-1\)时，\(g(y)>g(x)\)，

故只需要证明函数\(g(x)\)在\((e-1，+\infty)\)上单调递减即可。

以下用导数证明。

\(g'(x)=\cfrac{\cfrac{1}{x+1}\cdot e^x-ln(x+1)\cdot e^x}{(e^x)^2}=\cfrac{\cfrac{1}{x+1}-ln(x+1)}{e^x}\)，

令\(h(x)=\cfrac{1}{x+1}-ln(x+1)\)，

则\(h'(x)=-\cfrac{1}{(x+1)^2}-\cfrac{1}{x+1}=-\cfrac{x+2}{(1+x)^2}\)，

当\(x>e-1\)时，很显然\(h'(x)<0\)；

故函数\(h(x)\)在\((e-1，+\infty)\)上单调递减，

故\(h(x)<h(e-1)=\cfrac{1}{e}-1<0\)，

故导函数\(g'(x)=\cfrac{h(x)}{e^x}<0\)在\((e-1，+\infty)\)上恒成立，

故函数\(g(x)\)在\((e-1，+\infty)\)上单调递减，证毕。

【2017铜川模拟】【2020高三文科课时作业】不等式\(a^2+8b^2\geqslant \lambda b(a+b)\)对于任意的\(a\)，\(b\in R\)恒成立，则实数\(\lambda\)的取值范围为________．

法1：二次函数法，将\(b\)和\(\lambda\)看成系数，整理为关于\(a\)的二次函数恒成立问题求解；

由题可知，\(a^2+8b^2\geqslant \lambda b(a+b)\)对于任意的\(a\)，\(b\in R\)恒成立，

即\(a^2-\lambda b(a+b)+8b^2\geqslant 0\)对于任意的\(a\)，\(b\in R\)恒成立，

即\(a^2-\lambda ba+(8-\lambda)b^2\geqslant 0\)对于任意的\(a\in R\)恒成立，由二次函数性质可知，

\(\Delta=\lambda^2b^2-4(8-\lambda)b^2\leqslant 0\)，整理为\(b^2(\lambda^2+4\lambda -32)\leqslant 0\)

即\((\lambda+8)(\lambda-4)\leqslant 0\)，解得\(-8\leqslant \lambda \leqslant 4\)，即\(\lambda \in [-8，4]\)。

法2：二次函数法，将\(a\)和\(\lambda\)看成系数，整理为关于\(b\)的二次函数恒成立问题求解；

由题可知，\(a^2+8b^2\geqslant \lambda b(a+b)\)对于任意的\(a\)，\(b\in R\)恒成立，

即\(8b^2-\lambda b^2 -\lambda ab+a^2\geqslant 0\)对于任意的\(a\)，\(b\in R\)恒成立，

即\((8-\lambda)b^2 -\lambda ab+a^2\geqslant 0\)对于任意的\(b\in R\)恒成立，由二次函数性质可知，

当\(\lambda=8\)时，即\(-8ab+a^2\geqslant 0\)，不满足题意，故舍去；

当\(\left\{\begin{array}{l}{8-\lambda>0}\\{\Delta=\lambda^2a^2-4(8-\lambda)a^2\leqslant 0,}\end{array}\right.\) 解得\(-8\leqslant \lambda \leqslant 4\)，即\(\lambda \in [-8，4]\)。

解后反思：上述两种解法和判别式法求值域的算理是一致的。

法3：将\(\lambda\)看成参数，则不等式的两端是二次齐次式，故想到变量集中策略，

给不等式的两边同除以\(b^2\)，得到

即\(\cfrac{a^2}{b^2}+8\geqslant \lambda(\cfrac{a}{b}+1)\)恒成立，令\(\cfrac{a}{b}=t\in R\)，

则\(t^2-\lambda t+8-\lambda\geqslant 0\)对\(t\in R\)恒成立，故\(\Delta\leqslant 0\)，

即\(\Delta=(-\lambda)^2-4(8-\lambda)\leqslant 0\)，即\((\lambda+8)(\lambda-4)\leqslant 0\)，

解得\(-8\leqslant \lambda \leqslant 4\)，即\(\lambda \in [-8，4]\)。

已知\(a，b\in R^{+}\)，\(a+b-ab+3=0\)；1、求\(ab\)的范围；2、求\(a+b\)的范围；

1、求\(ab\)的范围；

解法1：\(\because -3+ab=a+b\ge 2\sqrt{ab}\)

\(\therefore ab-2\sqrt{ab}-3\ge 0\)，

\((\sqrt{ab}+1)(\sqrt{ab}-3) \ge 0\)

$\sqrt{ab}\leq -1 或 \sqrt{ab}\ge 3 $

又\(a，b\in R^{+}\)，故 \(\sqrt{ab}\ge 3\) (当且仅当\(a=b=3\)取到等号)

故\(ab\ge 9\)

解法2：由已知变形得到，\(a=\cfrac{b+3}{b-1}\)，由\(a>0\)得到\(b>1\)，

则\(ab=\cfrac{b+3}{b-1}b=\cfrac{b^2+3b}{b-1}=b-1+\cfrac{4}{b-1}+5\geqslant 2\sqrt{4}+5=9\)，

当且仅当\(b-1=\cfrac{4}{b-1}\)，即\(b=3=a\)时取到等号；

2、求\(a+b\)的范围；

解：\(\because a+b+3=ab \leq (\cfrac{a+b}{2})^2\)，令\(t=a+b\)

\(t^2-4t-12\ge0\)，解得\(t\leq -2\)或\(t\ge6\)；

故 \(a+b \ge 6\) (当且仅当\(a=b=3\)取到等号)

解法2：由已知变形得到，\(a=\cfrac{b+3}{b-1}\)，由\(a>0\)得到\(b>1\)，

则\(a+b=\cfrac{b+3}{b-1}+b=\cfrac{b-1+4}{b-1}+b=1+\cfrac{4}{b-1}+b=2+\cfrac{4}{b-1}+(b-1)\geqslant 2+2\sqrt{4}=6\)，

当且仅当\(b-1=\cfrac{4}{b-1}\)，即\(b=3=a\)时取到等号；

【评析】代数式中同时有\(a+b\)和\(ab\)型，两元\(a+b，ab\)常常转化集中为一元\(a+b\)或\(ab\)，这样就好处理多了。

【同类题】设\(m，n\in R\)，则直线\((m+1)x+(n+1)y-2=0\)与圆\((x-1)^2+(y-1)^2=1\)相切，且\(m+n\)的取值范围是_________。

分析：由圆心\((1 ,1)\)到直线的距离等于半径可得，

\(\cfrac{(m+1)\cdot 1+(n+1)\cdot 1-2}{\sqrt{(m+1)^2+(n+1)^2}}=1\) ，

变形得到\(mn=m+n+1\)，此时即转化为上述例3的类型了。

由\(mn\leq (\cfrac{m+n}{2})^2\)，则\(m+n+1\leq (\cfrac{m+n}{2})^2\)，

求解上述以\(m+n\)为整体的不等式，得到\(m+n\leq 2-2\sqrt{2}\)或者\(m+n\ge 2+2\sqrt{2}\)；

已知正实数\(a,b\)满足\(a+2b=1\)，求\(a^2+4b^2+\cfrac{1}{ab}\)的最小值。

法1：【错解】由\(a^2+4b^2+\cfrac{1}{ab}\ge 4ab+\cfrac{1}{ab}\ge 2\sqrt{4}=4\)，故所求的最小值是4。

错因分析：第一次使用均值不等式时等号成立的条件是\(a=2b\)，又由于必须满足条件\(a+2b=1\)，

可解得\(a=\cfrac{1}{2}\)，\(b=\cfrac{1}{4}\)；

而第二次使用均值不等式时等号成立的条件是\(4ab=\cfrac{1}{ab}\)，即\(ab=\cfrac{1}{2}\)，

而由上可知\(\cfrac{1}{ab}=8\)，二者不可能相等，故使用错误。

法2、由\(1=a+2b\ge 2\sqrt{2ab}\)，可得\(0<ab\leq \cfrac{1}{8}\)，当且仅当\(a=2b\)，即\(a=\cfrac{1}{2}\)，\(b=\cfrac{1}{4}\)时取等号；

则\(a^2+4b^2+\cfrac{1}{ab}=(a+2b)^2-4ab+\cfrac{1}{ab}=1-4ab+\cfrac{1}{ab}\)，令\(ab=t\in(0，\cfrac{1}{8}]\)，

则所求为\(1-4t+\cfrac{1}{t}=f(t)\)，\(t\in(0，\cfrac{1}{8}]\)，又\(f'(t)=-4-\cfrac{1}{t^2}<0\)，

故函数\(f(t)\)在\((0，\cfrac{1}{8}]\)上单调递减，故最小值为\(f(\cfrac{1}{8})=\cfrac{17}{2}\)。

【题组思路】

【模式1】：已知\(m>0，n>0\)，\(2m+n=3\)，求\(\cfrac{2}{m}+\cfrac{1}{n}\)的最小值。

分析：\(\cfrac{2}{m}+\cfrac{1}{n}=\cfrac{1}{3}(\cfrac{2}{m}+\cfrac{1}{n})(2m+n)\)\(=\cfrac{1}{3}(5+\cfrac{2n}{m}+\cfrac{2m}{n})\geqslant \cfrac{1}{3}(5+2\sqrt{4})=3\)

特征和思路：给定条件是整式，求分式的最值，常数代换,乘常数再除常数，部分使用均值不等式；

【模式2】：已知\(\cfrac{2}{m}+\cfrac{1}{n}=2，m>0，n>0\)，求 \(2m+n\)的最小值。

特征和思路：给定条件是分式，求整式的最值，常数代换,乘常数再除常数，部分使用均值不等式；

【模式3】：已知\(\cfrac{1}{a}+\cfrac{2}{b}=1，a>0，b>0\)，求\(\cfrac{2}{a-1}+\cfrac{1}{b-2}\)的最小值。^[1]

特征和思路：给定条件是分式，求分式的最值，变量集中，再使用均值不等式；

【模式4】：已知\(2a+b=1，a>0，b>0\)，求 \(a^2+2b^2\)的最小值。

特征和思路：给定条件是整式，求整式的最值，变量集中，用函数求解最值；

思路补充，直线和椭圆相切；

【2019天津滨海新区七所重点学校联考】若正实数\(x\)，\(y\)满足\(x+2y=5\)，则\(\cfrac{x^2-3}{x+1}+\cfrac{2y^2-1}{y}\)的最大值为_____________。

分析：由题可知，\(x>0\)，\(y>0\)，又由于\(x+2y=5\)，则\((x+1)+2y=6\)，

\(\cfrac{x^2-3}{x+1}+\cfrac{2y^2-1}{y}=\cfrac{(x+1)^2-2(x+1)-2}{x+1}+2y-\cfrac{1}{y}\)

\(=x+1-2+2y-(\cfrac{2}{x+1}+\cfrac{1}{y})\)

\(=x+2y-1-(\cfrac{2}{x+1}+\cfrac{1}{y})\)

\(=4-(\cfrac{2}{x+1}+\cfrac{1}{y})\)

\(=4-\cfrac{1}{6}(\cfrac{2}{x+1}+\cfrac{1}{y})\times [(x+1)+y]\)

\(=4-\cfrac{1}{6}(2+2+\cfrac{4y}{x+1}+\cfrac{x+1}{y})\)

\(\leqslant 4-\cfrac{1}{6}(4+2\sqrt{4})=\cfrac{8}{3}\),

当且仅当\(x+2y=5\)，\(x+1=2y\)，即\(x=2\)，\(y=\cfrac{3}{2}\)时取到等号；

则\(\cfrac{x^2-3}{x+1}+\cfrac{2y^2-1}{y}\)的最大值为\(\cfrac{8}{3}\).

解后反思：本题目用到分式变形，拆添项，常数代换，乘常数除常数等多种变形技巧。

已知 \(x>0\)，\(y>0\)，且满足 \(x-\sqrt{xy}-2y=0\) ，求值：\(\cfrac{2x-\sqrt{xy}}{y+\sqrt{xy}}\)

解：由于给定的方程为二元方程，故想到将其想办法变为一元方程，

两边同除以 \(y\) ，得到 \(\cfrac{x}{y}-\sqrt{\cfrac{x}{y}}-2=0\)，

令 \(\sqrt{\cfrac{x}{y}}=t\) ，则方程为\(t^2-t-2=0\)，得到\(t=2\)，或 \(t=-1\)(舍去)

故\(\sqrt{\cfrac{x}{y}}=2\)， \(\cfrac{x}{y}=4\) ，

将分式的分子分母同除以\(y\)，得到

\(\cfrac{2x-\sqrt{xy}}{y+\sqrt{xy}}=\cfrac{2\times\frac{x}{y}-\sqrt{\frac{x}{y}}}{1+\sqrt{\frac{x}{y}}}\)

\(=\cfrac{2\times4-2}{1+2\times2}=\cfrac{6}{5}\)

已知 \(x\geqslant 0\)， \(y \geqslant 0\)， 且 \(x+y=1\)， 则 \(x^{2}+y^{2}\) 的取值范围是_____________.

解法1：从数的角度入手分析，由于题目已知了两个元的关系 \(x+y=1\)，则可以将二元函数 \(x^2+y^2\) 表达式转化为一元二次函数的值域问题求解；

则将所求条件转化为 \(x^{2}+y^{2}=x^{2}+(1-x)^{2}=2x^{2}-2x+1\)，\(x \in[0,1]\)由 \(x\geqslant0\) 且 \(y=1-x\geqslant0\) ，解不等式组得到；，

所以当 \(x=0\) 或 \(1\) 时， 取最大值 \(1\) ； 当 \(x=\cfrac{1}{2}\) 时， 取最小值 \(\cfrac{1}{2}\)，

因此 \(x^{2}+y^{2}\) 的取值范围为 \(\left[\cfrac{1}{2}, 1\right]\).

解法2：从形的角度入手分析，也可以转化为几何关系求取值范围。

即 \(x \geq 0\)， \(y \geq 0\) ， \(x+y=1\) 表示线段\(AB\)，

那么 \(x^{2}+y^{2}\) 的几何意义就是线段上的动点到原点距离的平方，由图像能看到，当动点为点 \(A\) 或点 \(B\) 时，此时 \([x^{2}+y^{2}]_{\max}=1\)，

动点为点 \(C\) 时[可利用等面积法或直线和圆相切求解距离]，此时 \([x^{2}+y^{2}]_{\min}=\cfrac{1}{2}\)，因此 \(x^{2}+y^{2}\) 的取值范围为 \(\left[\cfrac{1}{2}, 1\right]\).

【学生问题】已知 \(x>y>0\)，求 \(\cfrac{x^2+y^2}{y(x-y)}\) 的最小值；

提示：本题目至少与二次齐次式，二元化为一元，分式函数变形三个常见的数学素材有关；

解：由于 \(x>y>0\)，则给原式分子分母同除以\(y^2\)[以便于二元化一元]，得到

原式\(=\cfrac{\cfrac{x^2}{y^2}+1}{\cfrac{x}{y}-1}\)， (令 \(\cfrac{x}{y}=t\)，则 \(t>1\)，实现了二元化为一元)

\(=\cfrac{t^2+1}{t-1}=\cfrac{[(t-1)+1]^2+1}{t-1}\)

\(=\cfrac{(t-1)^2+2(t-1)+2}{t-1}\) \(=(t-1)+2+\cfrac{2}{t-1}\)

\(=(t-1)+\cfrac{2}{t-1}+2\geqslant 2\sqrt{2}+2\)

当且仅当 \((t-1)=\cfrac{2}{t-1}\) 时，即 \(t=1+\sqrt{2}\) 时，取到等号；

故 \(\cfrac{x^2+y^2}{y(x-y)}\) 的最小值为 \(2\sqrt{2}+2\) ；

---

1. 已知\(\cfrac{1}{a}+\cfrac{2}{b}=1，a>0，b>0\)，得到\(0<\cfrac{2}{b}<1\)，得到\(b>2\)，
   由\(\cfrac{1}{a}+\cfrac{2}{b}=1\)，解得\(a=\cfrac{b}{b-2}\)，
   代入\(\cfrac{2}{a-1}+\cfrac{1}{b-2}=\cfrac{2}{\frac{b}{b-2}-1}+\cfrac{1}{b-2}\)\(=b-2+\cfrac{1}{b-2}\)\(\geqslant 2\)
   当且仅当\(b-2=\cfrac{1}{b-2}\)时，即\(b=3\)，\(a=3\)时取到等号； ↩︎