变量集中策略

公式定理💯随心记

【全概率公式】文字语言：将复杂事件分解为互斥事件的概率和。符号语言：若 $\bigcup\limits_{i=1}^n A_i=\Omega$ 且 $A_i\cap A_j=\varnothing$，则 $P (B)=\sum\limits_{i=1}^n P (A_i) P (B|A_i)$

---

前言

高中数学中的变量集中策略使用频次非常高，使用场景非常普遍，所以要好好学习掌握，并加以深刻体会。

相关概念

什么是变量集中策略？有什么优越性？这是我们急需要深入了解的知识。

变量集中策略，从字面的意思理解，是把散布在函数各处的的变量尽可能地统一到一处，把各种各样的不一样的变量尽可能地统一成一个变量，这样变量的个数减少了，出现变量的地方减少了，那么我们要处理的问题不就简单了吗！

如 $f(x)=\cfrac{x+2}{x+1}$ $(x\in[1，3])$，试判断函数的单调性，求值域；

如果我们单独看这个分式函数，在分子和分母上都有变量，当他们同时变大的时候，整体的结果到底怎么变化，我们还真不好说，但是如果我们施行了化为部分分式的变换后得到 $f(x)=\cfrac{x+2}{x+1}=1+\cfrac{1}{x+1}$，那么就能很容易的判断 $x\in [1，3]$ 时，函数 $f(x)$ 单调递减。原来在分子和分母上都有变量，变换后变量只出现在部分分式的分母位置上，这样就好判断多了，这里用到的就是数学中的变量集中策略和方法。

相关方法

尝试总结与变量集中策略相关的数学方法和数学变形。

• 分式裂项，化为部分分式；$\cfrac{b+c}{a}=\cfrac{b}{a}+\cfrac{c}{a}$;

• 分式的分子分母同除策略，将变量集中在分子或分母位置；

• 分母 $1=sin^2\theta+cos^2\theta$ 的代换；

• 配凑法；

• 换元法，代数换元和三角换元；

• 参数方程法；

相关阅读

• 1、分式型函数相关；

• 2、齐次式相关知识；

• 3、借助比例因子简化运算；

使用场景

【函数素材】已知函数 $f(x)=\begin{cases}x+1&0\leq x<1\\2^x-\frac{1}{2}&x>1\end{cases}$，若 $a>b\ge 0$，恒有 $f(a)=f(b)$，求 $b\cdot f(a)$ 的取值范围。

分析：先做出分段函数的图像如图所示，

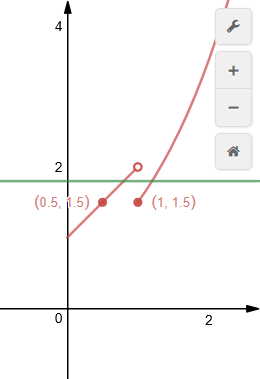
由图像可知 $0\leq b<1\leq a$，此时 $f(a)=2^a-\cfrac{1}{2}$，$f(b)=b+1$，

如果不做变换直接求 $b\cdot f(a)$ 的取值范围，会出现二元函数，

但是若利用 $f(a)=f(b)$，则 $b\cdot f(a)=b\cdot f(b)=b(b+1)$，就是一元函数，符合我们的求解习惯，

此时 $b\cdot f(a)=b\cdot f(b)=b(b+1)$，$x\in [\cfrac{1}{2}，1)$，就成了一元二次函数在限定区间上的值域问题了，

令 $g(b)=b(b+1)=(b+\cfrac{1}{2})^2-\cfrac{1}{4}$，在区间 $x\in [\cfrac{1}{2}，1)$ 上单调递增，

故 $g(\cfrac{1}{2})\leq g(b)<g(1)$，即 $b\cdot f(a)$ 的取值范围是 $[\cfrac{3}{4}，2)$。

【均值不等式】

$h(x)=\cfrac{x^2-4x+5}{x-2}=\cfrac{(x-2)^2+1}{x-2}=(x-2)+\cfrac{1}{x-2}\xrightarrow{x-2=t}t+\cfrac{1}{t}$，

【三角函数和解三角形】

$asin\theta+bcos\theta=\sqrt{a^2+b^2}sin(\theta+\phi)$，$2sin\theta\cdot cos\theta=sin2\theta$；

在三角形中，已知 $C-A=\cfrac{\pi}{2}$，则 $C=\cfrac{\pi}{2}+A$， $B=\pi-(A+C)=\pi-(A+\cfrac{\pi}{2}+A)=\cfrac{\pi}{2}-2A$；

【二元函数到一元函数】

• 比如：$\cfrac {x+2\sqrt {2xy}}{x+y}\xlongequal [再换元，令 \frac {y}{x}=t^2]{分子分母同除以 x}\cfrac {1+2\sqrt {2} t}{1+t^2}$

• 比如：$\cfrac{xy}{3x^2+xy-2y^2}=\cfrac{\cfrac{xy}{x^2}}{\cfrac{3x^2+xy-2y^2}{x^2}}$$=\cfrac{\cfrac{y}{x}}{3+\cfrac{y}{x}-2(\cfrac{y}{x})^2}$$=\cfrac{t}{3+t-2t^2}$$=\cfrac{1}{\cfrac{3}{t}+1-2t}$$(\cfrac {y}{x}=t，t 为斜率)$

【2018 届凤翔中学高三文科冲刺模拟第 10 套第 12 题】已知函数 $f(x)=ln\cfrac{x}{2}+\cfrac{1}{2}$，$g(x)=e^{x-2}$，若 $g(m)=f(n)$ 成立， 则 $n-m$ 的最小值为【】

$A.1-ln2$ $B.ln2$ $C.2\sqrt{e}-3$ $D.e^2-3$

分析：不妨设 $g(m)=f(n)=t$，则 $e^{m-2}=ln\cfrac{n}{2}+\cfrac{1}{2}=t(t>0)$，

(编者注：此处引入第三方变量 $t$，可以将 $m、n$ 用含有 $t$ 的表达式来刻画，则二元函数就此转化为了一元函数，我们就可以用导数求其最值了)

则 $m-2=lnt$，$m=2+lnt$；$ln\cfrac{n}{2}=t-\cfrac{1}{2}$，则 $n=2e^{t-\frac{1}{2}}$；

故 $n-m=2e^{t-\frac{1}{2}}-2-lnt(t>0)$ ，

令 $h(t)=2e^{t-\frac{1}{2}}-2-lnt(t>0)$，$h'(t)=2e^{t-\frac{1}{2}}-\cfrac{1}{t}$，(增 + 增 = 增)

易知 $h'(t)$ 在 $(0，+\infty)$ 上单调递增，且 $h(\cfrac{1}{2})=0$；

当 $t>\cfrac{1}{2}$ 时，$h'(t)>0$，当 $0<t<\cfrac{1}{2}$ 时，$h'(t)<0$，

即当 $t=\cfrac{1}{2}$ 时，$h(t)$ 取得极小值也是最小值，

$h(t)_{min}=h(\cfrac{1}{2})=2e^{\frac{1}{2}-\frac{1}{2}}-2-ln\cfrac{1}{2}=ln2$，故选 $B$.

【2016 第三次全国大联考第 16 题】若不等式 $2x^2+(1-a)y^2\ge (3+a)xy(x>0，y>0)$ 恒成立，求实数 $a$ 的最大值。

[法 1]：分离参数 + 构造函数，由题目可得 $a\leq \cfrac{2x^2+y^2-3xy}{y^2+xy}$，

令 $f (x,y)= \cfrac {2x^2+y^2-3xy}{y^2+xy}\xlongequal [关于 x，y 的二次齐次式]{分子分母同除以 y^2}$$\cfrac{2(\cfrac{x}{y})^2-3\cfrac{x}{y}+1}{1+\cfrac{x}{y}}\\$$\xlongequal [令 \cfrac {x}{y}=t>0]{二元变一元} g (t)$$=\cfrac{2t^2-3t+1}{t+1}$$=2(t+1)+\cfrac{6}{t+1}-7\ge 2\sqrt{12}-7$$=4\sqrt{3}-7$

当且仅当 $t=\sqrt{3}-1$ 时取到等号。故有 $a\leqslant 4\sqrt{3}-7$，所以 $a_{max}=4\sqrt{3}-7$。

[法 2]：二元变量集中为一元变量，两边同除以 $y^2$，得到 $2(\cfrac{x}{y})^2-(a+3)(\cfrac{x}{y})+(1-a)\ge 0$，

令 $\cfrac{x}{y}=t>0$，即 $2t^2-(a+3)t+(1-a)\geqslant 0$ 对任意 $t>0$ 恒成立，

令 $g(t)=2t^2-(a+3)t+(1-a)$ ，则分以下两种情形：

$1^。$ $\Delta=a^2+14a+1\leqslant 0$，解得 $-4\sqrt{3}-7\leqslant a \leqslant 4\sqrt{3}-7$；

$2^。$ $\begin{cases}\Delta >0\\\cfrac{a+3}{2\cdot 2}<0\\g(0)=1-a\ge 0\end{cases}$，解得 $a<-4\sqrt{3}-7$；

综上可知，$a\leqslant 4\sqrt{3}-7$，故 $a_{max}=4\sqrt{3}-7$。

【使用在解方程中：二元方程变为一元方程】

$a^2-3ab+2b^2=0\Rightarrow(\cfrac{a}{b})^2-3(\cfrac{a}{b})+2=0$

【三角变换中的三个角到一个角】

$\begin{align*}\cfrac{c\cdot cos(30^{\circ}-A)}{b+a}&=\cfrac{sinC\cdot cos(30^{\circ}-A)}{sinB+sinA}\\&=\cfrac{sinC\cdot cos(30^{\circ}-A)}{sin(\cfrac{\pi}{3}-A)+sinA}\\&=\cfrac{\cfrac{\sqrt{3}}{2}\cdot(\cfrac{\sqrt{3}}{2}cosA+\cfrac{1}{2}sinA)}{\cfrac{\sqrt{3}}{2}cosA+\cfrac{1}{2}sinA}\\&=\cfrac{\sqrt{3}}{2}\end{align*}$.

【2017 宝鸡中学高三理科第一次月考第 10 题】已知函数 $f(x)=\cfrac{2sinxcosx}{1+sinx+cosx}$，$x\in(0，\cfrac{\pi}{2}]$ 的最大值为 $M$，最小值为 $N$，则 $M-N$=？

分析：令 $sinx+cosx=t$ ，由于 $x\in(0，\cfrac{\pi}{2}]$，

则 $t=sinx+cosx=\sqrt{2}sin(x+\cfrac{\pi}{4})\in [1，\sqrt{2}]$，则 $2sinxcosx=t^2-1$，

故 $f(x)=\cfrac{t^2-1}{t+1}=g(t)=t-1$，

故 $f(x)_{max}=M=\sqrt{2}-1$；$f(x)_{min}=N=0$；即 $M-N=$$\sqrt{2}-1$。

【不等式 [证明]】

比如：已知 $x_1>x_2>0$，证明 $ln(\cfrac{x_1}{x_2})>2\cfrac{x_1-x_2}{x_1+x_2}$.

分析：令 $\cfrac{x_1}{x_2}=t$，则 $t>1$；$ln(\cfrac{x_1}{x_2})>2\cfrac{x_1-x_2}{x_1+x_2}$ 等价于 $lnt>2\cfrac{t-1}{t+1}$；然后作差构造函数 $g(t)=lnt-2\cfrac{t-1}{t+1}$，想办法证明 $g(t)>0$ 恒成立即可。

【不等式求解中】已知 $a，b\in R^{+}$，$a+b-ab+3=0$；

1、求 $ab$ 的范围；

解：$\because -3+ab=a+b\ge 2\sqrt{ab}$

$\therefore ab-2\sqrt{ab}-3\ge 0$，

$(\sqrt{ab}+1)(\sqrt{ab}-3) \ge 0$

$\sqrt {ab}\leq -1 或 \sqrt {ab}\ge 3$

又 $a，b\in R^{+}$，故 $\sqrt{ab}\ge 3$ (当且仅当 $a=b=3$ 取到等号)

故 $ab\ge 9$

2、求 $a+b$ 的范围；

解：$\because a+b+3=ab \leq (\cfrac{a+b}{2})^2$，令 $t=a+b$

$t^2-4t-12\ge0$，解得 $t\leq -2$ 或 $t\ge6$；

故 $a+b \ge 6$ (当且仅当 $a=b=3$ 取到等号)

【评析】代数式中同时有 $a+b$ 和 $ab$ 型，两元 $a+b，ab$ 常常转化集中为一元 $a+b$ 或 $ab$，这样就好处理多了。

【同类题】设 $m，n\in R$，则直线 $(m+1)x+(n+1)y-2=0$ 与圆 $(x-1)^2+(y-1)^2=1$ 相切，且 $m+n$ 的取值范围是_________。

分析：由圆心 $(1 ,1)$ 到直线的距离等于半径可得，

$\cfrac{(m+1)\cdot 1+(n+1)\cdot 1-2}{\sqrt{(m+1)^2+(n+1)^2}}=1$ ，

变形得到 $mn=m+n+1$，此时即转化为上述例 3 的类型了。

由 $mn\leq (\cfrac{m+n}{2})^2$，则 $m+n+1\leq (\cfrac{m+n}{2})^2$，

求解上述以 $m+n$ 为整体的不等式，得到 $m+n\leq 2-2\sqrt{2}$ 或者 $m+n\ge 2+2\sqrt{2}$；

已知实数 $a，b，c$ 满足 $a+b+c=9$，$ab+bc+ac=24$，则 $b$ 的取值范围是 $[1，5]$。

解：由于 $ab+bc+ac=(a+c)b+ac=24$

故 $ac=24-(a+c)b \leq (\cfrac{a+c}{2})^2$

故 $24-(a+c)b \leq (\cfrac{a+c}{2})^2$，(三元变成了两个元 $a+c，b$)

又因为 $a+c=9-b$，

即 $24-(9-b)b \leq \cfrac{(9-b)^2}{4}$,(两元 $a+c，b$ 变成了一元 $b$)

即 $b^2-6b+5 \leq 0$

解得 $1\leq b \leq 5$

【线性规划中】

$z=\cfrac{3x+4y+10}{x+2}=\cfrac{3(x+2)+4y+4}{x+2}=3+4\times\cfrac{y+1}{x+2}$；$\cfrac {y-(-1)}{x-(-2)} 为斜率$；

$z=\cfrac{x^2+y^2}{xy}=\cfrac{y}{x}+\cfrac{x}{y}=k+\cfrac{1}{k}(\cfrac{y}{x}=k)$；

【由平面直角坐标系到极坐标系的换系过程中】

在刻画距离 $OP$ 时，在平面直角坐标系中 $|OP|=\sqrt{x^2+y^2}$，为二元根式函数；在极坐标系中 $|OP|=\rho$，为一元一次函数；

【参数方程中】

圆 $C：x^2+y^2=4$ 上的任意点 $P$，当点 $P(x，y)$ 表达的时候，是二元的，但是换成参数方程时，点 $P(2cos\theta，2sin\theta)$ 表达时，就是一元函数了；

椭圆 $C：\cfrac{x^2}{9}+\cfrac{y^2}{4}=1$ 上的任意点 $P$，当点 $P(x，y)$ 表达的时候，是二元的，但是换成参数方程时，点 $P(3cos\theta，2sin\theta)$ 表达时，就是一元函数了；

【比例中、等幂中】

• 已知 $a:b:c=2:3:4$，引入非零因子 $k$，则可以这样表达，$a=2k，b=3k，c=4k$，可以看成 $a，b，c$ 都是 $k$ 的一元函数了。

• 令 $e^{m-2}=ln\cfrac{n}{2}+\cfrac{1}{2}=t(t>0)$，

(编者注：此处引入第三方变量 $t$，可以将 $m、n$ 用含有 $t$ 的表达式来刻画，则二元函数就此转化为了一元函数，我们就可以用导数求其最值了)

则 $m-2=lnt$，$m=2+lnt$；$ln\cfrac{n}{2}=t-\cfrac{1}{2}$，则 $n=2e^{t-\frac{1}{2}}$；

故 $n-m=2e^{t-\frac{1}{2}}-2-lnt(t>0)$ ，

【2017 全国卷 1 理科第 11 题】【等幂】已知 $2^x=3^y=5^z$，比较 $2x、3y、5z$ 的大小；

分析：令 $2^x=3^y=5^z=k$，则 $x=log_2k=\cfrac{lgk}{lg2}$，$y=log_3k=\cfrac{lgk}{lg3}$，$z=log_5k=\cfrac{lgk}{lg5}$，

故 $2x=\cfrac{2lgk}{lg2}=\cfrac{lgk}{\cfrac{1}{2}lg2}=\cfrac{lgk}{lg\sqrt{2}}$，$3y=\cfrac{3lgk}{lg3}=\cfrac{lgk}{\cfrac{1}{3}lg3}=\cfrac{lgk}{lg\sqrt[3]{3}}$，$5z=\cfrac{5lgk}{lg5}=\cfrac{lgk}{\cfrac{1}{5}lg5}=\cfrac{lgk}{lg\sqrt[5]{5}}$，

接下来，法 1：转化为只需要比较 $\sqrt[2]{2}$，$\sqrt[3]{3}$，$\sqrt[5]{5}$ 三者的大小即可。

先比较 $\sqrt[2]{2}$，$\sqrt[3]{3}$，给两个式子同时 6 次方，得到 $(\sqrt[2]{2})^6=2^3=8$，$(\sqrt[3]{3})^6=3^2=9$，故 $\sqrt[2]{2}<\sqrt[3]{3}$，则 $\cfrac{lgk}{lg\sqrt[2]{2}}>\cfrac{lgk}{lg\sqrt[3]{3}}$，即得到 $2x>3y$

再比较 $\sqrt[2]{2}$，$\sqrt[5]{5}$，给两个式子同时 10 次方，得到 $(\sqrt[2]{2})^{10}=2^5=32$，$(\sqrt[5]{5})^{10}=5^2=25$，故 $\sqrt[2]{2}>\sqrt[5]{5}$，则 $\cfrac{lgk}{lg\sqrt[2]{2}}<\cfrac{lgk}{lg\sqrt[3]{3}}$，即得到 $5z>2x$，综上得到 $3y<2x<5z$

法 2：作商法，$\cfrac{2x}{3y}=\cfrac{2}{3}\cdot \cfrac{lg3}{lg2}=\cfrac{lg9}{lg8}=log_89>1$，故 $2x>3y$；

$\cfrac{5z}{2x}=\cfrac{5}{2}\cdot \cfrac{lg2}{lg5}=\cfrac{lg2^5}{lg5^2}=log_{25}32>1$，故 $5z>2x$；故 $3y<2x<5z$。

难点题目

已知正实数 $x、y、z$ 满足 $x^2-3xy+4y^2-z=0$，当 $\cfrac{xy}{z}$ 取得最大值时，求 $\cfrac{2}{x}+\cfrac{1}{y}-\cfrac{2}{z}$ 的最大值．

分析：$z=x^2-3xy+4y^2\ge 2x\cdot 2y-3xy=xy$，当且仅当 $x=2y$ 时取得等号；

则 $\cfrac{1}{z}\leq \cfrac{1}{xy}$，当且仅当 $x=2y$ 时取得等号；

则 $\cfrac{xy}{z}\leq \cfrac{xy}{xy}=1$，即 $\cfrac{xy}{z}$ 的最大值为 $1$，当且仅当 $x=2y$ 时取得等号；

此时，$z=x^2-3xy+4y^2=4y^2-3y\cdot 2y+4y^2=2y^2$，

$\cfrac{2}{x}+\cfrac{1}{y}-\cfrac{2}{z}=\cfrac{2}{2y}+\cfrac{1}{y}-\cfrac{2}{2y^2}$

$=\cfrac{2}{y}-\cfrac{1}{y^2}=-(\cfrac{1}{y}-1)^2+1\leq 1$，

故 $\cfrac{2}{x}+\cfrac{1}{y}-\cfrac{2}{z}$ 的最大值为 1．

此时，$y=1，x=2，z=2$；

【点评】变量集中，三元变一元。

【2018 河南郑州一模】若对于任意的正整数 $x$，$y$ 都有 $(2x-\cfrac{y}{e})\cdot ln\cfrac{y}{x}\leq \cfrac{x}{me}$ 成立，则实数 $m$ 的取值范围是【】

$A.(\cfrac{1}{e}，1)$ $B.(\cfrac{1}{e^2}，1]$ $C.(\cfrac{1}{e^2}，e]$ $D.(0，\cfrac{1}{e}]$

分析：先将给定的式子通分变形为 $\cfrac{2ex-y}{e}\cdot ln\cfrac{y}{x}\leq \cfrac{x}{me}$，两边同乘以 $\cfrac{e}{x}$，

再次变形为 $(2e-\cfrac{y}{x})\cdot ln\cfrac{y}{x}\leq \cfrac{1}{m}$，

令 $\cfrac{y}{x}=t>0$，则不等式变形为 $(2e-t)\cdot lnt\leq \cfrac{1}{m}$，

令 $h(t)=(2e-t)\cdot lnt$，则需要求 $h(t)_{max}$；

$h'(x)=(-1)lnt+(2e-t)\cdot \cfrac{1}{t}=\cfrac{-t(lnt+1)+2e}{t}$，

先用观察法或经验找到导函数的分子的零点 $t=e$，

当 $t\in (0，e)$ 时，$h'(t)>0$，$h(t)$ 单调递增，当 $t\in (e，+\infty)$ 时，$h'(t)<0$，$h(t)$ 单调递减，

故 $h(t)_{max}=h(e)=e$，即 $\cfrac{1}{m}\ge e$，解得 $0<m\leq \cfrac{1}{e}$；故选 $D$。

【2019$\cdot$ 北京高考】已知函数 $f(x)=\cfrac{1}{4}x^3-x^2+x$，

(1). 求曲线 $y=f(x)$ 的斜率为 $1$ 的切线方程；

解：$f'(x)=\cfrac{3}{4}{x}^2-2x+1$，

由 $f'(x)=1$ 得 $\cfrac{3}{4}{x}^2-2x+1=1$，

整理得到 $x(x-\cfrac{8}{3})=0$，解得 $x_{1}=0$， $x_{2}=\cfrac{8}{3}$，

又 $f(0)=0$，$f(\cfrac{8}{3})=\cfrac{8}{27}$

即切点分别为 $(0,0)$ 和 $(\cfrac{8}{3},\cfrac{8}{27})$

故由点斜式得到切线方程分别为 $y-0=1\cdot(x-0)$ 和 $y-\cfrac{8}{27}=1\cdot(x-\cfrac{8}{3})$，

即切线方程分别为 $y=x$ 和 $y=x-\cfrac{64}{27}$.

(2). 当 $x \in[-2,4]$ 时，求证: $x-6\leqslant f(x)\leqslant x$.

解：对所要证明的结论作以适当的注意到双联不等式的左右端都有自变量 $x$，且同号，如果给不等式同时减去 $x$，则此双联不等式就会将自变量全部集中到中部一个位置，此处实际上使用了变量集中策略，$\quad$ 转化，

只需证 $-6\leqslant f(x)-x \leqslant 0$，这样问题就转化为求函数 $f(x)-x$ 在 $[-2,4]$ 上的值域问题了。

令 $g(x)=f(x)-x=\cfrac{1}{4}x^{3}-x^{2}$，$x\in[-2,4]$，

则 $g'(x)=\cfrac{3}{4}x^2-2x=\cfrac{3}{4}x(x-\cfrac{8}{3})$，

可知 $g'(x)$ 在 $[-2,0]$ 为正，在 $(0, \cfrac{8}{3})$ 为负，在 $[\cfrac{8}{3}, 4]$ 为正，

又 $g(-2)=-6$， $g(0)=0$， $g(\cfrac{8}{3})=-\cfrac{64}{27}>-6$， $g(4)=0$

则 $-6\leqslant g(x)\leqslant 0$，故 $x-6\leqslant f (x)\leqslant x$，证毕.

已知 $log_2x=log_3y=log_5z<-1$，则 【$\quad$】

$A.2x < 3y < 5z$ $B.5z < 3y < 2x$ $C.3y < 2x < 5z$ $D.5z < 2x < 3y$

解析：大胆引入第四个变量 $t$ ，以便于实现变量集中的设想，方便解题；

设 $t=log_2x=log_3y=log_5z<-1$，则依次得到，

$x=2^t$， $y=3^t$， $z=5^t$，到此就实现了变量的集中，便于下一步的运算和思考；

则 $2x=2^{t+1}$， $3y=3^{t+1}$， $5z=5^{t+1}$，

又由于 $t<-1$， 得到 $t+1<0$，故由幂函数的单调性或者指数函数的图像可知，

$5^{t+1}<3^{t+1}<2^{t+1}$，即 $5z<3y<2x$ ，即选 $B$.

构造函数 $f(x)=\log_x{(x+1)}$， 则 $f(x)=\log_x{(x\cdot\cfrac{x+1}{x})}=\log_xx+\log_x\cfrac{x+1}{x}=1+\log_x{(1+\cfrac{1}{x})}$，

用电脑验证，该函数的定义域为 $(0,1)\cup(1,+\infty)$，单调递减区间是 $(0,1)$ 和 $(1,+\infty)$，