用样本猜总体的秘密武器，4大抽样分布总结

数据分析时，我们经常需要从样本数据推断总体特征。

而抽样分布就是连接样本与总体的重要桥梁，如果你不理解它，就无法理解为什么我们可以通过调查几千人来预测全国的选举结果，也无法理解A/B测试背后的逻辑。

本文将尽量使用大白话和Python代码，带你彻底搞懂抽样分布，并掌握最常用的四大分布：Z分布、T分布、卡方分布和F分布。

1. 什么是抽样分布

想象一下，你想了解全市高中生的平均身高，由于时间和资源限制，你不可能测量每个学生。

你的做法是：

去学校随机挑选100位学生（这是一个样本，Sample）。

计算这100位学生的平均身高，比如是150cm（这是统计量，Statistic）。

但是，一次抽样可靠吗？

如果你运气不好，刚好选到的学生都是个子偏高的怎么办？

于是，你决定重复这个过程：

第2次，再选100位学生，算平均值是155cm。

第3次，再选100位学生，算平均值是148cm。

……

你重复了1000次。

现在，你手里有了1000个“平均身高”的数据。如果你把这1000个数据画成一个直方图，这个图展示的分布，就是抽样分布。

一句话定义：

抽样分布不是原始数据的分布，而是统计量（如平均值、方差）的概率分布。

2. 抽样分布的重要性

在现实工作中，我们通常只有一次抽样的机会（因为成本太高），我们手里只有一个样本数据。

我们面临的终极问题是：

既然我看不到总体（所有中学生身高），我怎么敢用手里这唯一的样本（100位学生的身高）去代表总体？

抽样分布 就是连接 “样本” 和 “总体” 的桥梁：

总体是未知的真相，样本是我们手里的碎片。

抽样分布告诉我们：样本统计量围绕总体真值波动的规律。

知道了这个规律（分布），我们就能算出：我手里这个样本，有多大的概率是靠谱的？

这就是置信区间和假设检验的基础。

3. 四大常用抽样分布

接下来，我们介绍四种最常用的抽样分布，并使用Python代码来做简单的演示。

3.1. Z分布

Z分布是统计学中的“皇冠”。

当样本量足够大（通常n > 30）时，根据中心极限定理，样本均值的分布近似于正态分布。

使用Z分布的前提是，假设已知总体方差，或者样本量极大以至于样本方差可以代替总体方差。

它的使用场景一般在大样本的均值检验（如：网站百万流量下的转化率分析）。

这种方法的优点在于其数学性质非常好，查表非常方便，而且计算过程也很简单。

然而，它也存在一些局限性，在现实生活中，我们很难准确地知道整个群体的方差情况。

此外，在样本数量较少的情况下，使用这种方法可能会导致较大的误差。

下面用代码模拟一个Z分布的示例。

import numpy as np
import scipy.stats as stats

# 演示Z分布在置信区间计算中的应用
# 假设我们调查了100名学生的月支出，平均值为2500元，已知总体标准差为500元
sample_mean = 2500   # 样本平均值
population_std = 500 # 总体标准差
sample_size = 100    # 样本数量
confidence_level = 0.95  # 置信水平

# 计算标准误差
standard_error = population_std / np.sqrt(sample_size)

# 计算Z值 (95%置信水平对应的Z值)
z_value = stats.norm.ppf((1 + confidence_level) / 2)

# 计算置信区间
margin_of_error = z_value * standard_error
confidence_interval = (sample_mean - margin_of_error, sample_mean + margin_of_error)

print(f"样本均值: {sample_mean}元")
print(f"95%置信区间: [{confidence_interval[0]:.2f}, {confidence_interval[1]:.2f}]元")
print(
    f"这意味着我们有95%的把握认为总体平均月支出在{confidence_interval[0]:.2f}元到{confidence_interval[1]:.2f}元之间"
)

# 运行结果：
'''
样本均值: 2500元
95%置信区间: [2402.00, 2598.00]元
这意味着我们有95%的把握认为总体平均月支出在2402.00元到2598.00元之间
'''

代码中用到了scipy库中的stats.norm.ppf()函数，这是累积分布函数(CDF)的反函数，可用来计算Z值。

使用测试数据绘制的图如下：

# 生成Z分布数据
x = np.linspace(-4, 4, 1000)
z_distribution = stats.norm.pdf(x)

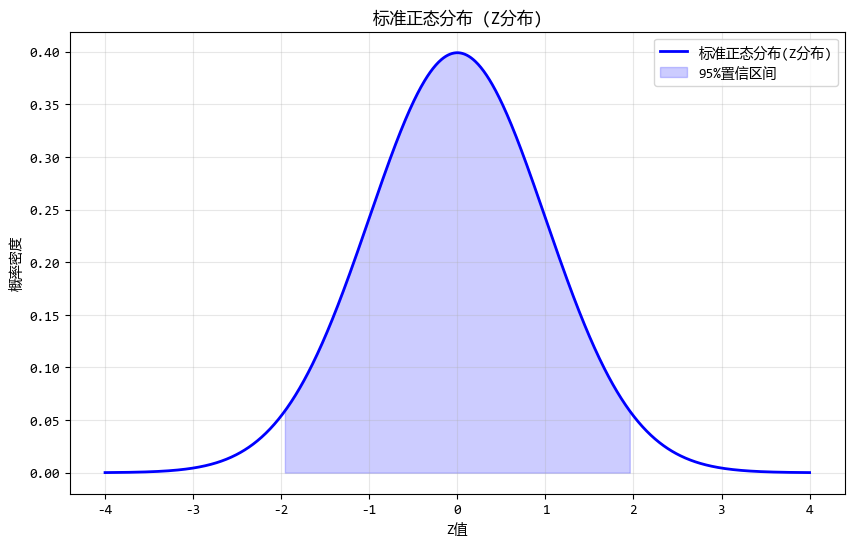
3.2. T分布

T分布是为了解决 “小样本”问题而生的。

当你手头数据很少（比如n < 30），且不知道总体方差时，Z分布会低估误差，这时候必须用T分布。

比如，在小样本实验（比如只有10只小白鼠参与的药物实验）或AB测试的早期阶段中，优先考虑使用T分布。

当处理小规模的数据集时，T分布能够提供更加准确的结果。

这是因为T分布具有所谓的“厚尾”特征，这意味着它对于数据中的不确定性给予了更多的关注，特别是提高了对极端值出现可能性的认可。

这样的特性使得在面对有限数量样本的情况下，T分布相较于Z分布而言，能更真实地反映出数据的变异程度。

然而，T分布并非没有缺点。

随着收集到的数据量不断增加，我们会观察到T分布逐渐趋向于标准正态分布，也就是我们常说的Z分布。

这表明，在大规模数据集面前，T分布所提供的额外灵活性变得不那么显著了。

下面用代码模拟一个T分布的示例。

# T分布在置信区间计算中的应用
# 假设我们调查了25名员工的月薪，平均值为8000元，样本标准差为1500元
sample_mean = 8000  # 样本平均值
sample_std = 1500   # 样本标准差
sample_size = 25    # 样本数量
confidence_level = 0.95   # 置信水平

# 计算标准误
standard_error = sample_std / np.sqrt(sample_size)

# 计算T值 (95%置信水平，自由度=n-1)
t_value = stats.t.ppf((1 + confidence_level) / 2, sample_size - 1)

# 计算置信区间
margin_of_error = t_value * standard_error
confidence_interval = (sample_mean - margin_of_error, sample_mean + margin_of_error)

print(f"样本均值: {sample_mean}元")
print(f"样本标准差: {sample_std}元")
print(f"样本大小: {sample_size}")
print(f"95%置信区间: [{confidence_interval[0]:.2f}, {confidence_interval[1]:.2f}]元")
print(f"注意：由于样本量较小且总体方差未知，我们使用T分布而不是Z分布")

# 运行结果：
'''
样本均值: 8000元
样本标准差: 1500元
样本大小: 25
95%置信区间: [7380.83, 8619.17]元
注意：由于样本量较小且总体方差未知，我们使用T分布而不是Z分布
'''

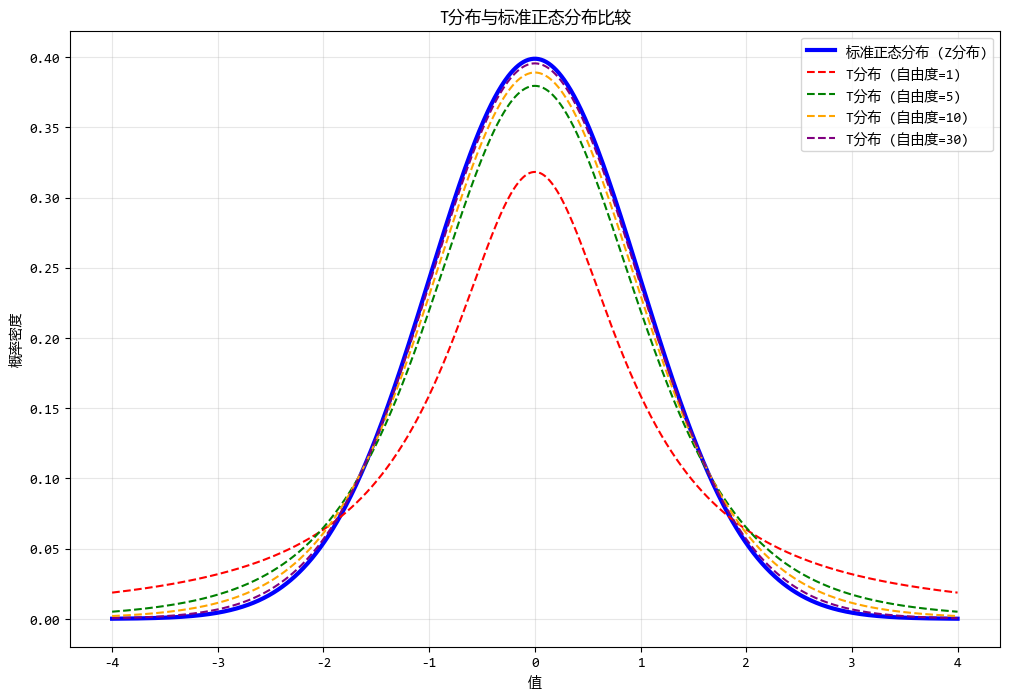
使用测试数据绘制不同自由度的T分布图形如下：

# 生成数据
x = np.linspace(-4, 4, 1000)
z_distribution = stats.norm.pdf(x)

# 绘制不同自由度的T分布
degrees_of_freedom = [1, 5, 10, 30]

for df in degrees_of_freedom:
    t_distribution = stats.t.pdf(x, df)

3.3. 卡方分布

前两个分布主要用于处理 “数值型” 数据（平均值），而 卡方分布 主要用于 “类别型” 数据。

卡方分布的主要应用场景有：

独立性检验：性别和购买偏好是否有关系？
拟合优度检验：这枚骰子是否均匀（实际观测频数 vs 理论期望频数）？
方差的检验：生产零件的波动率是否在控制范围内？

卡方分布在处理非数值型数据，比如分类数据时特别有用。

不过，它也有一定的局限性，首先，它对样本数量有一定的要求，通常每个类别中的样本数不能太少，否则结果可能不太准确。

另外，这种方法得到的结果分布是不对称的，并且只会出现正值。

下面用代码模拟一个卡方分布的示例。

# 卡方分布在独立性检验中的应用示例
# 模拟一个问卷调查数据：性别与产品偏好是否独立
# 创建模拟数据
observed = np.array(
    [[30, 20, 10], [15, 25, 20]]  # 男性选择A、B、C产品的人数
)  # 女性选择A、B、C产品的人数

print("观察到的列联表:")
print("        产品A  产品B  产品C")
print(f"男性    {observed[0][0]}    {observed[0][1]}    {observed[0][2]}")
print(f"女性    {observed[1][0]}    {observed[1][1]}    {observed[1][2]}")

# 执行卡方独立性检验
chi2_stat, p_value, dof, expected = stats.chi2_contingency(observed)

print(f"\n卡方检验结果:")
print(f"卡方统计量: {chi2_stat:.4f}")
print(f"P值: {p_value:.4f}")
print(f"自由度: {dof}")

alpha = 0.05
if p_value < alpha:
    print("结论: 拒绝原假设，性别与产品偏好之间存在显著关联")
else:
    print("结论: 无法拒绝原假设，性别与产品偏好之间没有显著关联")

# 运行结果：
'''
观察到的列联表:
        产品A  产品B  产品C
男性    30    20    10
女性    15    25    20

卡方检验结果:
卡方统计量: 8.8889
P值: 0.0117
自由度: 2
结论: 拒绝原假设，性别与产品偏好之间存在显著关联
'''

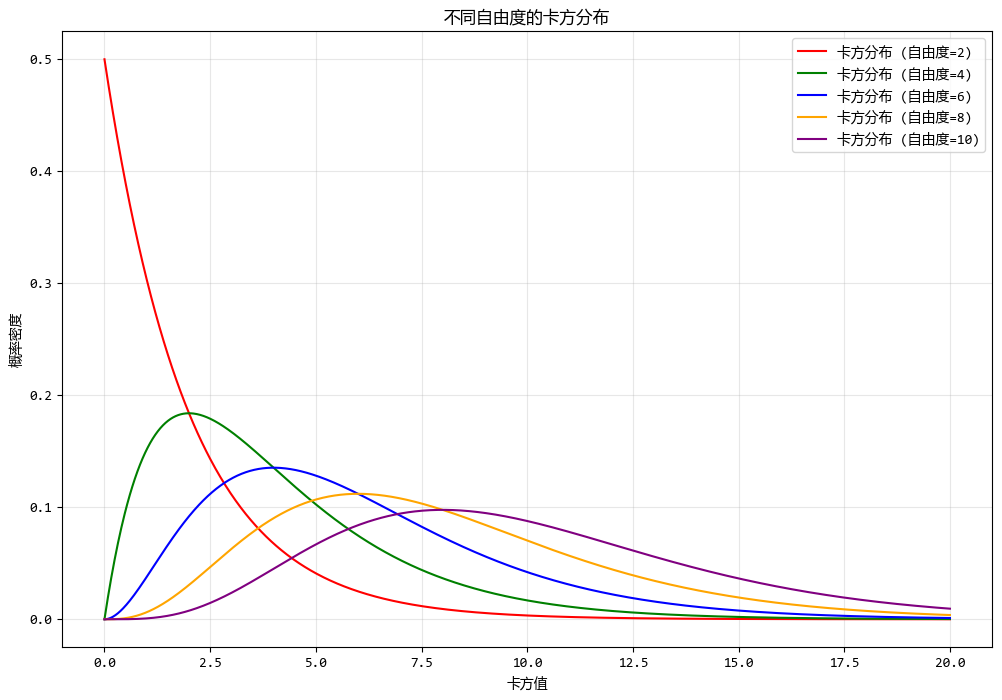
使用测试数据绘制不同自由度的卡方分布图形如下：

x = np.linspace(0, 20, 1000)
degrees_of_freedom_chi2 = [2, 4, 6, 8, 10]

for df in degrees_of_freedom_chi2:
    chi2_distribution = stats.chi2.pdf(x, df)

3.4. F分布

F分布主要关注两个方差的比率。如果说T检验是比 “均值” ，那F检验就是比 “波动” 。

F分布的主要应用场景有：

方差分析 (ANOVA)：比较3组及以上数据的均值差异（本质是比较组间方差和组内方差的比值）。
比较两个总体方差：机器A和机器B生产的产品，谁的质量更稳定？

F分布是ANOVA分析的核心，它的优势在于它能够同时处理多组数据之间的差异。

然而，其局限性表现在对数据正态性假设的敏感度较高。

下面用代码模拟一个F分布的示例。

# F分布在方差分析中的应用示例
# 模拟三种不同教学方法下学生的考试成绩
np.random.seed(42)  # 确保结果可重现

# 生成三个组的模拟成绩数据
method_a = np.random.normal(75, 8, 30)  # 教学方法A
method_b = np.random.normal(80, 10, 30)  # 教学方法B
method_c = np.random.normal(72, 9, 30)  # 教学方法C

# 执行单因素方差分析
f_stat, p_value = stats.f_oneway(method_a, method_b, method_c)

print("方差分析(ANOVA)示例: 比较三种教学方法的效果")
print(
    f"教学方法A: 平均分 = {np.mean(method_a):.2f}, 标准差 = {np.std(method_a, ddof=1):.2f}"
)
print(
    f"教学方法B: 平均分 = {np.mean(method_b):.2f}, 标准差 = {np.std(method_b, ddof=1):.2f}"
)
print(
    f"教学方法C: 平均分 = {np.mean(method_c):.2f}, 标准差 = {np.std(method_c, ddof=1):.2f}"
)
print(f"\n方差分析结果:")
print(f"F统计量: {f_stat:.4f}")
print(f"P值: {p_value:.4f}")

alpha = 0.05
if p_value < alpha:
    print("结论: 拒绝原假设，至少有一种教学方法的效果与其他方法有显著差异")
else:
    print("结论: 无法拒绝原假设，三种教学方法的效果没有显著差异")

# 运行结果：
'''
方差分析(ANOVA)示例: 比较三种教学方法的效果
教学方法A: 平均分 = 73.49, 标准差 = 7.20
教学方法B: 平均分 = 78.79, 标准差 = 9.31
教学方法C: 平均分 = 72.12, 标准差 = 8.93

方差分析结果:
F统计量: 5.1166
P值: 0.0079
结论: 拒绝原假设，至少有一种教学方法的效果与其他方法有显著差异
'''

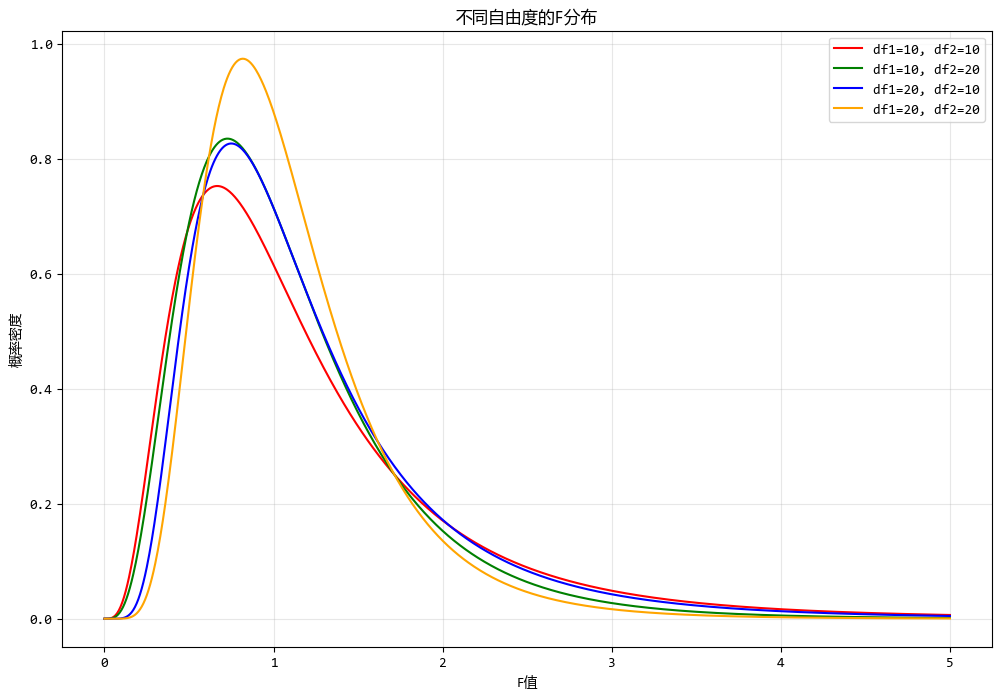
使用测试数据绘制不同自由度的F分布图形如下：

x = np.linspace(0, 5, 1000)
# 定义几组自由度组合
df_combinations = [(10, 10), (10, 20), (20, 10), (20, 20)]

for (df1, df2) in df_combinations:
    f_distribution = stats.f.pdf(x, df1, df2)

4. 总结

最后，为了理清思路，我整理了一个对比表格。

当我们面对数据时，可以按图索骥：

分布名称	核心关键词	典型应用场景	数据类型
Z分布	大样本、标准	样本量>30，已知总体方差的均值检验	数值型 (Continuous)
T分布	小样本、修正	样本量<30，未知总体方差，AB测试	数值型 (Continuous)
卡方分布	分类、独立性	检验男女是否偏好不同，骰子是否均匀	类别型 (Categorical) / 方差
F分布	多组比较、方差比	ANOVA方差分析（3组以上均值对比）	数值型 (比率)

数据分析不仅仅是敲代码（Python）或画图（Tableau/Excel），其灵魂在于统计思维。

抽样分布告诉我们要对随机性保持敬畏：不要轻信一次结果，要看这次结果在分布中的位置。

posted @ 2025-12-05 15:39 wang_yb 阅读(0) 评论(0) 收藏举报

刷新页面返回顶部

千里之行，始于足下