【8*】点分治学习笔记
前言
为什么我的点分治和点分树怎么写都很丑啊。这就是算法不可貌相吗......
这个知识点时间跨度也比较长,所以码风比较零碎,我认为模板题中的码风比较优异。
前置知识:【6】树的DFS序、直径、重心 中树的重心部分。
长文警告:本文一共 \(1068\) 行,请合理安排阅读时间。
此类知识点大纲中并未涉及,所以【8】是我自己的估计,后带星号表示估计,仅供参考。
点分治
点分治是处理树上路径问题的高效手段,通常会结合各种数据结构进行维护。
我们考虑在树上进行分治操作。每次选择一个点,统计通过此节点的路径信息,然后删除此节点,递归遍历得到的几棵子树。
统计通过此节点的路径信息时,我们一般把路径拆成两部分,一条路径为两棵不同子树中的节点到这个节点的路径拼起来。一棵子树中所有节点分别到这个节点的信息一般可以通过 DFS 求出。有时我们也会加入一个空路径表示只选一棵子树中的路径。这个拼起来的过程就像序列分治合并左右区间的过程,通常需要数据结构手段来辅助。
由于我们每次随便选择一个点,因此我们不妨选择树的重心。由于树的重心的性质,每棵子树大小至多为 \(O(\frac{n}{2})\),相当于每次折半,所以单纯点分治的时间复杂度为 \(O(n\log n)\)。而且由于一般跑不满(只有链能跑满),所以常数比较优秀。
下面给出点分治的一般模板。findroot 是找根,calc 是计算子树大小,dsu 是点分治主函数。有一些细节,注意标记和判断已经删除的节点,以及求子树重心时更新总结点数。
inline void findroot(int x,int fa)
{
int mx=0;
siz[x]=1;
for(int i=h[x];i;i=e[i].nxt)
if(e[i].v!=fa&&!del[e[i].v])findroot(e[i].v,x),siz[x]+=siz[e[i].v],mx=max(mx,siz[e[i].v]);
mx=max(mx,tn-siz[x]);
if(mx<=tn/2)rth=x;
}
inline void calc(int x,int fa)
{
siz[x]=1;
for(int i=h[x];i;i=e[i].nxt)
if(e[i].v!=fa&&!del[e[i].v])calc(e[i].v,x),siz[x]+=siz[e[i].v];
}
inline void dsu(int x,int fa)
{
del[x]=1;
//在这里遍历子树处理路径信息
for(int i=h[x];i;i=e[i].nxt)
if(!del[e[i].v])calc(e[i].v,x),tn=siz[e[i].v],findroot(e[i].v,x),dsu(rth,x);
}
点分治中处理路径的方式有两种,一种是依次遍历子树,把之前的子树的路径的贡献加入数据结构,遍历新的子树;另一种是把所有子树路径加入一个数据结构,然后依次遍历每个子树路径,容斥掉同一棵子树中的两条路径。
点分治例题
例题 \(1\) :
点分治模板题。由于只需要统计有没有出现过,我们依次遍历每一棵子树。考虑把之前的路径的长度加入一个 bool 类型的桶,然后遍历这一棵子树的路径,用 \(k\) 减去路径的长度得到 \(c\),查询之前的桶中有没有长度为 \(c\) 的路径,如果有,那这两条路径拼起来长度就为 \(k\) 了。
注意对于一棵子树,我们先遍历并计算子树路径的贡献,再把子树路径加入数据结构,因为同一棵子树的路径通过这种方式计算会出问题。最好一次点分治处理所有询问以减小常数。时间复杂度 \(O(nm\log n)\)。
#include <bits/stdc++.h>
using namespace std;
struct edge
{
int v,w,nxt;
}e[20000];
int n,m,u,v,w,h[20000],del[20000],siz[20000],k[200],ans[200],tn=0,rt=0,cnt=0;
vector<int>s;
bool t[20000000];
void add_edge(int u,int v,int w)
{
e[++cnt].nxt=h[u];
e[cnt].v=v;
e[cnt].w=w;
h[u]=cnt;
}
void findroot(int x,int fa)
{
int mx=0;
siz[x]=1;
for(int i=h[x];i;i=e[i].nxt)
if(e[i].v!=fa&&!del[e[i].v])findroot(e[i].v,x),siz[x]+=siz[e[i].v],mx=max(mx,siz[e[i].v]);
mx=max(mx,tn-siz[x]);
if(mx<=tn/2)rt=x;
}
void dfs(int x,int fa,int dis)
{
siz[x]=1;
if(dis<=1e7)s.push_back(dis);
for(int i=h[x];i;i=e[i].nxt)
if(e[i].v!=fa&&!del[e[i].v])dfs(e[i].v,x,dis+e[i].w),siz[x]+=siz[e[i].v];
}
void dsu(int x)
{
del[x]=1,t[0]=1;
for(int i=h[x];i;i=e[i].nxt)
if(!del[e[i].v])
{
dfs(e[i].v,x,e[i].w);
for(int i=0;i<(int)s.size();i++)
for(int j=1;j<=m;j++)
if(k[j]>=s[i]&&t[k[j]-s[i]])ans[j]=1;
for(int i=0;i<(int)s.size();i++)t[s[i]]=1;
s.clear();
}
t[0]=0;
for(int i=h[x];i;i=e[i].nxt)
if(!del[e[i].v])
{
dfs(e[i].v,x,e[i].w);
for(int i=0;i<(int)s.size();i++)t[s[i]]=0;
s.clear();
}
for(int i=h[x];i;i=e[i].nxt)
if(!del[e[i].v])tn=siz[e[i].v],findroot(e[i].v,x),dsu(rt);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n-1;i++)scanf("%d%d%d",&u,&v,&w),add_edge(u,v,w),add_edge(v,u,w);
for(int i=1;i<=m;i++)scanf("%d",&k[i]);
tn=n,findroot(1,0),dsu(rt);
for(int i=1;i<=m;i++)
if(ans[i])printf("AYE\n");
else printf("NAY\n");
return 0;
}
例题 \(2\) :
和上一个题基本一样,但是由于查询的是 \(\le k\) 的路径数量,所以需要记录出现次数。并且,考虑一条长度为 \(c\) 路径与之前的路径拼合时需要查询长度 \(\le k-c\) 的路径,即查前缀和。再考虑到每次加入路径时是单点修改,所以考虑使用树状数组维护。时间复杂度 \(O(n\log^2 n)\)。
码风古早,非常丑陋,并不可取。
#include <bits/stdc++.h>
using namespace std;
struct edge
{
long long v,next,dis;
}e[400010];
long long n,k,s[200010],h[200010],d[200010],del[200010],he=0,cnt=0,ans=99999999,tol=0;
long long f[200010],g[200010];
void add_edge(long long u,long long v,long long d)
{
e[++cnt].next=h[u];
e[cnt].v=v;
e[cnt].dis=d;
h[u]=cnt;
}
long long lowbit(long long x)
{
return x&(-x);
}
void add(long long x,long long s)
{
if(x==0)
{
g[0]+=k;
return;
}
while(x<=k)g[x]+=s,x+=lowbit(x);
}
long long getsum(long long x)
{
long long ans=0;
while(x>0)ans+=g[x],x-=lowbit(x);
return ans+g[0];
}
long long dfs(long long now,long long pre,long long cnt)
{
long long maxn=0;
s[now]=1,d[now]=0;
if(del[now])return 0;
for(long long i=h[now];i;i=e[i].next)
if(e[i].v!=pre)
{
long long z=dfs(e[i].v,now,cnt);
s[now]+=z,maxn=max(maxn,z);
}
if(max(maxn,cnt-s[now])<ans)ans=min(ans,max(maxn,cnt-s[now])),he=now;
return s[now];
}
void getdep(long long now,long long pre)
{
if(del[now])return;
for(long long i=h[now];i;i=e[i].next)
if(e[i].v!=pre)
{
d[e[i].v]=d[now]+e[i].dis;
getdep(e[i].v,now);
}
}
void count(long long now,long long pre)
{
if(del[now])return;
if(d[now]<=k)tol+=getsum(k-d[now]),f[d[now]]++;
for(long long i=h[now];i;i=e[i].next)
if(e[i].v!=pre)count(e[i].v,now);
}
void update(long long now,long long pre)
{
if(del[now])return;
if(d[now]<=k)add(d[now],f[d[now]]),f[d[now]]=0;
for(long long i=h[now];i;i=e[i].next)
if(e[i].v!=pre)update(e[i].v,now);
}
void clear(long long now,long long pre)
{
if(del[now])return;
if(d[now]<=k)add(d[now],-1);
for(long long i=h[now];i;i=e[i].next)
if(e[i].v!=pre)clear(e[i].v,now);
}
void dfz(long long now,long long siz)
{
if(del[now])return;
ans=99999999;
dfs(now,0,siz);
for(long long i=h[he];i;i=e[i].next)
{
d[e[i].v]=e[i].dis;
getdep(e[i].v,he);
}
g[0]=1;
for(long long i=h[he];i;i=e[i].next)
{
count(e[i].v,he);
update(e[i].v,he);
}
for(long long i=h[he];i;i=e[i].next)clear(e[i].v,he);
del[he]=1;
for(long long i=h[he];i;i=e[i].next)dfz(e[i].v,s[e[i].v]);
}
int main()
{
scanf("%lld",&n);
for(long long i=1;i<=n-1;i++)
{
long long u=0,v=0,d=0;
scanf("%lld%lld%lld",&u,&v,&d);
add_edge(u,v,d);add_edge(v,u,d);
}
scanf("%lld",&k);
dfz(1,n);
printf("%lld",tol);
return 0;
}
例题 \(3\) :
假设当前处理的树根为 \(x\),我们考虑如何统计经过点 \(x\) 的合法路径。
\(1\):存在一个与 \(x\) 颜色相同的点,且这个点到 \(x\) 的路径上没有与之颜色相同的点,那么这个点和 \(x\) 就构成了一条合法路径。
\(2\):存在一个与 \(x\) 颜色不相同的点,且这个点到 \(x\) 的路径上没有与之颜色相同的点。那么这个点与 \(x\) 的其他子树中与之颜色相同的点构成一条合法路径。
情况 \(2\) 可以通过记录一个颜色数组,将访问过的到 \(x\) 的路径上没有与之颜色相同的点的节点的颜色进行统计。两棵不同的子树之间的路径匹配时,直接使用颜色数组即可。
接下来就是点分治模板了。每次取重心,统计贡献,删除,递归点分治子树。即可统计所有合法路径。时间复杂度 \(O(n\log n)\)。
码风比较古早,实现得比较差,常数较大。
#include <bits/stdc++.h>
using namespace std;
struct edge
{
long long v,nxt;
}e[600000];
long long t,n,a[300000],s[300000],h[300000],del[300000],he=0,cnt=0,ans=1e10,tol=0;
long long pre[300000],x[300000],sum[300000],g[300000];
void init()
{
for(int i=1;i<=n;i++)del[i]=0,h[i]=0;
tol=0,cnt=0;
}
void add_edge(long long u,long long v)
{
e[++cnt].nxt=h[u];
e[cnt].v=v;
h[u]=cnt;
}
long long dfs1(long long now,long long fa,long long cnt)
{
long long maxn=0;
s[now]=1;
if(del[now])return 0;
for(long long i=h[now];i;i=e[i].nxt)
if(e[i].v!=fa)
{
long long z=dfs1(e[i].v,now,cnt);
s[now]+=z,maxn=max(maxn,z);
}
if(max(maxn,cnt-s[now])<ans)ans=min(ans,max(maxn,cnt-s[now])),he=now;
return s[now];
}
void dfs2(long long now,long long fa)
{
if(del[now])return;
s[now]=1,pre[now]=x[a[now]],x[a[now]]=now;
if(pre[now]==0)
{
if(a[now]==a[he])tol++;
else
{
tol+=sum[a[now]];
g[a[now]]++;
}
}
for(long long i=h[now];i;i=e[i].nxt)
if(e[i].v!=fa)
{
dfs2(e[i].v,now);
if(del[e[i].v]==0)s[now]+=s[e[i].v];
}
x[a[now]]=pre[now];
}
void update(long long now,long long fa)
{
if(del[now])return;
sum[a[now]]+=g[a[now]],g[a[now]]=0;
for(long long i=h[now];i;i=e[i].nxt)
if(e[i].v!=fa)update(e[i].v,now);
}
void clear(long long now,long long fa)
{
if(del[now])return;
pre[now]=0,x[a[now]]=0,sum[a[now]]=0;
for(long long i=h[now];i;i=e[i].nxt)
if(e[i].v!=fa)clear(e[i].v,now);
}
void dfz(long long now,long long siz)
{
if(del[now])return;
ans=1e10;
dfs1(now,0,siz);
for(long long i=h[he];i;i=e[i].nxt)
{
dfs2(e[i].v,he);
update(e[i].v,he);
}
for(long long i=h[he];i;i=e[i].nxt)clear(e[i].v,he);
del[he]=1;
for(long long i=h[he];i;i=e[i].nxt)dfz(e[i].v,s[e[i].v]);
}
int main()
{
scanf("%lld",&t);
while(t--)
{
scanf("%lld",&n);
init();
for(long long i=1;i<=n;i++)scanf("%lld",&a[i]);
for(long long i=1;i<=n-1;i++)
{
long long u=0,v=0;
scanf("%lld%lld",&u,&v);
add_edge(u,v),add_edge(v,u);
}
dfz(1,n);
printf("%lld\n",tol);
}
return 0;
}
例题 \(4\) :
前 \(k\) 大问题通常转化为第 \(k\) 大。我们先二分求出第 \(k\) 大路径长度,即求出使小于其的路径数小于 \(k\) 的最大路径长度,判定的话通过例题 \(2\) 的方式就行了,然后暴力合并找出前 \(k\) 大路径,差的用第 \(k\) 大路径长度补齐,时间复杂度 \(O(n\log^3 n)\)。
我们考虑优化。不难发现树都结构在每次二分中是不变的,因此我们考虑把每次点分治的结果预处理出来,然后二分时直接使用。
我们发现原本树状数组的思路并不好预处理,考虑更换方式,把所有子树的路径预处理出来一起处理。考虑贡献,我们把所有路径按长度排序,从小到大遍历每一条路径,通过双指针求出数量。注意还需要减去同一棵子树中的路径合并的方案,所以还需要记录每一条路径来自哪一棵子树,开桶记录合并时每一棵子树的路径分别有多少个,把同一棵子树中的路径减掉。
这样每次双指针是 \(O(n)\) 的,带上二分总复杂度 \(O(n\log^2 n)\)。预处理首先有点分治的复杂度,然后对点分治得到的点进行排序,总复杂度也为 \(O(n\log^2n)\)。于是我们很暴力地优化掉了一个 \(\log\)。
注意暴力合并找出前 \(k\) 大路径双指针时也需要用子树来源的桶存每一条路径,不然每次遍历可能会被卡回 \(O(n^2)\),虽然题目没有卡。写起来非常精神污染。
#include <bits/stdc++.h>
using namespace std;
struct node
{
int v,w,nxt;
}e[200000];
int n,m,u,v,w,h[200000],siz[200000],del[200000],t[200000],st[400000],top=0,tn=0,cnt=0,rt=0;
long long ans=0;
vector<pair<int,int> >s[200000];
vector<int>p[200000],q;
void add_edge(int u,int v,int w)
{
e[++cnt].nxt=h[u];
e[cnt].v=v;
e[cnt].w=w;
h[u]=cnt;
}
void findroot(int x,int fa)
{
int mx=0;
siz[x]=1;
for(int i=h[x];i;i=e[i].nxt)
if(e[i].v!=fa&&!del[e[i].v])findroot(e[i].v,x),siz[x]+=siz[e[i].v],mx=max(mx,siz[e[i].v]);
mx=max(mx,tn-siz[x]);
if(mx<=tn/2)rt=x;
}
void dfs(int x,int fa,int rt,int id,int dis)
{
siz[x]=1,s[rt].push_back({dis,id});
for(int i=h[x];i;i=e[i].nxt)
if(e[i].v!=fa&&!del[e[i].v])dfs(e[i].v,x,rt,id,dis+e[i].w),siz[x]+=siz[e[i].v];
}
void calc(int x,int fa)
{
siz[x]=1;
for(int i=h[x];i;i=e[i].nxt)
if(e[i].v!=fa&&!del[e[i].v])calc(e[i].v,x),siz[x]+=siz[e[i].v];
}
void dsu1(int x)
{
del[x]=1,s[x].push_back({0,0});
for(int i=h[x];i;i=e[i].nxt)
if(!del[e[i].v])dfs(e[i].v,x,x,e[i].v,e[i].w);
for(int i=h[x];i;i=e[i].nxt)
if(!del[e[i].v])tn=siz[e[i].v],findroot(e[i].v,x),dsu1(rt);
}
void dsu2(int x,int v)
{
del[x]=1;
int k=(int)s[x].size()-1,sum=0;
for(int j=0;j<(int)s[x].size();j++)
{
while(s[x][k].first+s[x][j].first>=v&&k>=0)t[s[x][k].second]++,sum++,k--;
ans+=(sum-t[s[x][j].second]);
}
for(int j=0;j<(int)s[x].size();j++)t[s[x][j].second]=0;
for(int i=h[x];i;i=e[i].nxt)
if(!del[e[i].v])calc(e[i].v,x),tn=siz[e[i].v],findroot(e[i].v,x),dsu2(rt,v);
}
void dsu3(int x,int v)
{
del[x]=1;
int k=(int)s[x].size()-1;
for(int j=0;j<(int)s[x].size();j++)
{
while(s[x][k].first+s[x][j].first>=v&&k>=0)
{
p[s[x][k].second].push_back(s[x][k].first);
if(p[s[x][k].second].size()==1)q.push_back(s[x][k].second);
k--;
}
for(int l=0;l<(int)q.size();l++)
if(q[l]<s[x][j].second)
for(int o=0;o<(int)p[q[l]].size();o++)
st[++top]=s[x][j].first+p[q[l]][o];
}
q.clear();
for(int i=0;i<(int)s[x].size();i++)p[s[x][i].second].clear();
for(int i=h[x];i;i=e[i].nxt)
if(!del[e[i].v])calc(e[i].v,x),tn=siz[e[i].v],findroot(e[i].v,x),dsu3(rt,v);
}
int check(int mid)
{
memset(del,0,sizeof(del));
tn=n,ans=0,findroot(1,0),dsu2(rt,mid+1);
ans/=2;
return ans;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n-1;i++)scanf("%d%d%d",&u,&v,&w),add_edge(u,v,w),add_edge(v,u,w);
tn=n,findroot(1,0),dsu1(rt);
for(int i=1;i<=n;i++)
if(s[i].size())sort(s[i].begin(),s[i].end());
int l=0,r=5e8,ans=0;
while(l<=r)
{
int mid=(l+r)>>1;
if(check(mid)<m)r=mid-1,ans=mid;
else l=mid+1;
}
memset(del,0,sizeof(del)),tn=n,findroot(1,0),dsu3(rt,ans+1);
while(top<m)st[++top]=ans;
sort(st+1,st+top+1);
for(int i=top;i>=1;i--)printf("%d\n",st[i]);
return 0;
}
本题还有一种比较帅的做法,使用 P2048 [NOI2010] 超级钢琴 中的优先队列维护多路前 \(k\) 大的技巧。即把点分治的过程中的路径拍成一个序列,使每条路径可以选择的路径的范围是一个区间,就变成了 P2048 [NOI2010] 超级钢琴。
点分树
考虑把点分治的过程记录下来,将分成的若干个子连通块的重心连向当前整个树的重心,依次递归,最终可以建出一棵树,我们将这棵树称作点分树。
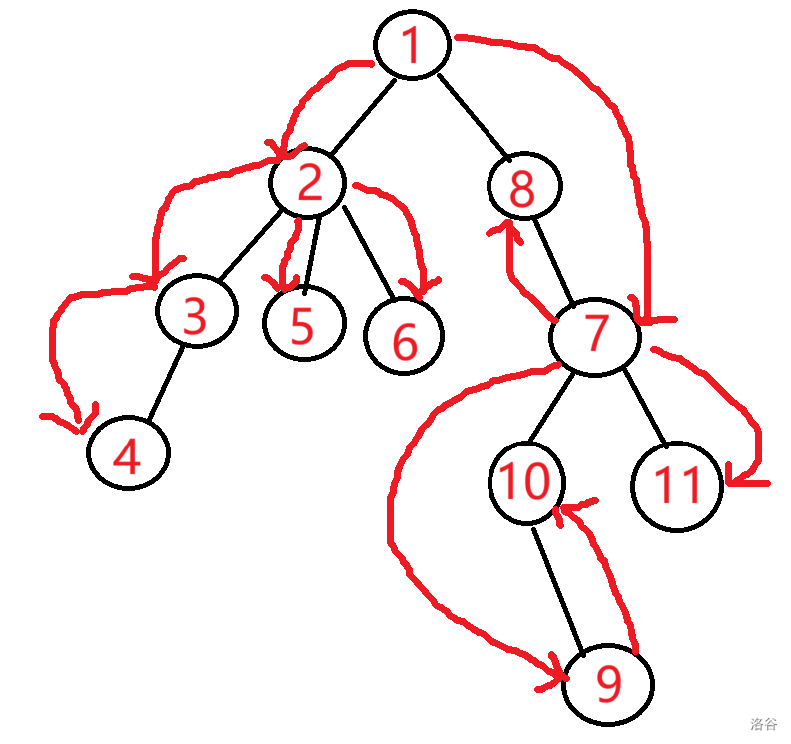
这就是一棵点分树。图中黑边表示原树的边,红边表示点分树的边,数字表示点分树上的 DFS 序。
点分树和原树的关系十分微弱,但是如果题目要求的东西与原树形态关系不大,例如路径问题,连通块问题,关键点问题,就可以利用点分树的特殊性质解决。
点分树具有如下关键性质。
\(1\):深度为 \(O(\log n)\)。
\(2\):点 \(x\) 和点 \(y\) 在点分树上的 \(\text{lca}(x,y)\) 是原树上 \(x\) 到 \(y\) 的路径的必经点。
\(3\):点分树上的一棵子树对应原树上的一个连通块。
点分树的题目有几个套路。
维护路径信息
因为点分树的边在原树上没有任何意义,因此我们对于某个节点维护子树内信息和子树内节点到这个点的父节点的信息。
然后计算信息的时候,由于性质 \(1\) 和性质 \(2\),我们暴力跳父节点,这是在枚举 \(\text{lca}(x,y)\)。这样,我们就可以通过在 \(\text{lca}(x,y)\) 处划分路径来统计信息了。我们通常会利用容斥处理信息,即先统计 \(x\) 子树内的信息,再统计 \(x\) 的父节点子树内的信息,然后减去 \(x\) 子树内到 \(x\) 的父节点的信息,以此类推,这样就不重不漏地统计了信息。
这是一份示例代码。其中 vf[x] 表示 \(x\) 在点分树上的父节点,query(rt[x]) 表示以 \(x\) 为根的点分树子树信息,query(rtf[x]) 表示以 \(x\) 为根的点分树子树到 \(x\) 的父节点的子树信息。对 ans 的加减旨在体现容斥,实际中可以根据实际情况调整。
int ask(int x,int k)
{
int ans=query(rt[x]),st=x,t=0;
while(x)
{
t=x,x=vf[x];
ans+=query(rt[x]);
ans-=query(rtf[t]);
}
return ans;
}
由于树高为 \(O(\log n)\) 级别的,所以我们修改一个节点的权值后可以暴力跳父节点更新子树内信息。因此,点分树支持单点修改,所以又称动态点分治。
这是一份示例代码。其中 update(rt[x],k) 表示更新以 \(x\) 为根的点分树子树信息,update(rtf[x],k) 表示以 \(x\) 为根的点分树子树到 \(x\) 的父节点的子树信息。
inline void access(int x,int k)
{
int st=x;
while(x)
{
update(rt[x],k);
if(vf[x])update(rtf[x],k);
x=vf[x];
}
}
寻找关键点
根据性质 \(3\),如果能通过判断与这个点的直连边来判断需要寻找的关键点在删除这个点后哪棵子树中,那我们可以通过在点分树上走边来寻找关键点。不难发现这样一定能走到关键点。
我们通过数据结构维护某个点的儿子节点,快速查找出满足条件的儿子,并走向其子树的重心,也就是在点分树上走向其所在的子树。直到不能再走了,此时这个点就是关键点。由于点分树的树高为 \(O(\log n)\),所以不计数据结构寻找关键点的时间复杂度为 \(O(\log n)\)。
这个技巧一般初始位置为整棵点分树的根,不然有可能遍历不了整棵树导致漏解。同时这个技巧也不适用于查询子树,因为点分树上的子树与原树的子树没有任何关系。
这是一份示例代码。其中 findnxt(x) 表示 \(x\) 在点分树上的满足关键点在这个儿子点分树上的子树对应的连通块中的儿子,一般通过数据结构查询。
int move(int x)
{
int k=findnxt(x);
if(k)return move(k);
return pr;
}
点分树例题
例题 \(5\) :
考虑如何维护子树内到 \(x\) 距离小于 \(k\) 的点的权值和。对每个 \(x\),我们维护一棵以距离为下标的动态开点线段树,维护内容为权值和。查询距离为 \(k\) 以内的点权就在线段树上查询 \([0,k]\) 的权值和就行了。维护子树内的点到子树根节点父节点的信息也是同理。
修改是容易的。考虑查询,暴力跳父节点,由于合并路径,此时到这个父节点 \(f\) 距离小于等于 \(k-\text{dis}(x,f)\) 的点在原树上与 \(x\) 距离不大于 \(k\),同样的方式查询,其中 \(\text{dis}(x,f)\) 表示 \(x\) 和 \(f\) 在原树上的距离。然后减掉 \(x\) 子树内的点到 \(f\) 的同样的信息就行了,这个已经维护过了。
写丑了,点分树不需要建出来,实际上一般记个父节点就行了,最多用 vector 存个儿子。而且 \(\text{lca}\) 最好使用 \(O(1)\) 的 \(\text{dfn}\) 序 \(\text{lca}\)。这个写法常数巨大,建议采用例题 \(7\) 的写法。
#include <bits/stdc++.h>
using namespace std;
struct edge
{
int v,nxt;
}e[200000];
struct node
{
int sum;
}tr[8000000];
int n,m,u[200000],v[200000],w[200000],op,x,y,a[200000],h[200000],siz[200000],del[200000],dep[200000],q[200000],fa[200000][20],la[200000][20],rt[200000],rtf[200000],lc[8000000],rc[8000000],top=0,cnt=0,cnd=0,tn=0,rth=0,rtb=0,las=0;
inline void add_edge(int u,int v)
{
e[++cnt].nxt=h[u];
e[cnt].v=v;
h[u]=cnt;
}
inline void dfs(int x,int pr)
{
dep[x]=dep[pr]+1,fa[x][0]=pr;
for(int i=1;i<=19;i++)
if(fa[x][i-1])fa[x][i]=fa[fa[x][i-1]][i-1];
else break;
for(int i=h[x];i;i=e[i].nxt)
if(e[i].v!=pr)dfs(e[i].v,x);
}
inline void getf(int x,int pr)
{
q[x]=pr;
for(int i=h[x];i;i=e[i].nxt)
if(e[i].v!=pr)getf(e[i].v,x);
}
inline int lca(int x,int y)
{
if(dep[x]>dep[y])swap(x,y);
int c=dep[y]-dep[x];
for(int i=19;i>=0;i--)
if(c&(1<<i))y=fa[y][i];
if(x==y)return x;
for(int i=19;i>=0;i--)
if(fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];
return fa[x][0];
}
inline int getdis(int x,int y)
{
return dep[x]+dep[y]-2*dep[lca(x,y)];
}
inline int gotdis(int x,int y,int l)
{
return dep[x]+dep[y]-2*dep[la[x][l]];
}
inline void findroot(int x,int fa)
{
int mx=0;
siz[x]=1;
for(int i=h[x];i;i=e[i].nxt)
if(e[i].v!=fa&&!del[e[i].v])findroot(e[i].v,x),siz[x]+=siz[e[i].v],mx=max(mx,siz[e[i].v]);
mx=max(mx,tn-siz[x]);
if(mx<=tn/2)rth=x;
}
inline void calc(int x,int fa)
{
siz[x]=1;
for(int i=h[x];i;i=e[i].nxt)
if(e[i].v!=fa&&!del[e[i].v])calc(e[i].v,x),siz[x]+=siz[e[i].v];
}
inline void dsu(int x,int fa)
{
del[x]=1;
if(fa)u[++top]=fa,v[top]=x;
for(int i=h[x];i;i=e[i].nxt)
if(!del[e[i].v])calc(e[i].v,x),tn=siz[e[i].v],findroot(e[i].v,x),dsu(rth,x);
}
inline void pushup(int x)
{
tr[x].sum=tr[lc[x]].sum+tr[rc[x]].sum;
}
inline void insert(int &x,int l,int r,int p,int k)
{
if(!x)x=++cnd;
if(l==r)
{
tr[x].sum+=k;
return;
}
int mid=(l+r)>>1;
if(p<=mid)insert(lc[x],l,mid,p,k);
else insert(rc[x],mid+1,r,p,k);
pushup(x);
}
inline int query(int x,int l,int r,int lx,int rx)
{
if(!x)return 0;
if(l>=lx&&r<=rx)return tr[x].sum;
int mid=(l+r)>>1,ans=0;
if(lx<=mid)ans+=query(lc[x],l,mid,lx,rx);
if(rx>=mid+1)ans+=query(rc[x],mid+1,r,lx,rx);
return ans;
}
inline void ances(int x)
{
int st=x,dep=1;
while(x)la[st][dep]=lca(st,x),dep++,x=q[x];
}
inline void access(int x,int k)
{
int st=x;
while(x)
{
insert(rt[x],0,n-1,getdis(st,x),k);
if(q[x])insert(rtf[x],0,n-1,getdis(st,q[x]),k);
x=q[x];
}
}
inline int ask(int x,int k)
{
int ans=query(rt[x],0,n-1,0,k),st=x,t=0,dep=1;
while(x)
{
dep++,t=x,x=q[x];
int l=gotdis(st,x,dep);
if(k-l>=0)
{
ans+=query(rt[x],0,n-1,0,k-l);
ans-=query(rtf[t],0,n-1,0,k-l);
}
}
return ans;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=n-1;i++)scanf("%d%d",&u[0],&v[0]),add_edge(u[0],v[0]),add_edge(v[0],u[0]);
dfs(1,0),tn=n,findroot(1,0),rtb=rth,dsu(rth,0);
memset(h,0,sizeof(h)),cnt=0;
for(int i=1;i<=top;i++)add_edge(u[i],v[i]),add_edge(v[i],u[i]);
getf(rtb,0);
for(int i=1;i<=n;i++)ances(i),access(i,a[i]);
for(int i=1;i<=m;i++)
{
scanf("%d",&op);
if(op==1)scanf("%d%d",&x,&y),x^=las,y^=las,access(x,-a[x]),a[x]=y,access(x,a[x]);
else scanf("%d%d",&x,&y),x^=las,y^=las,las=ask(x,y),printf("%d\n",las);
}
return 0;
}
例题 \(6\) :
还是考虑在点分树上维护信息。考虑维护一个节点不同子树内的关灯的节点到这个点的最长和次长路径,在这个节点直接合并就是这个连通块内经过这个节点的最长路径。
由于灯可能会再打开,所以需要支持撤销。因此,我们用可删堆维护每个节点不同子树内的节点到这个点的最长和次长路径,再用一个可删堆维护所有节点的最长路径,就可以支持撤销和 \(O(1)\) 查询了。
为了便于对每个点维护子树内关灯的节点到这个点的最长和次长路径,我们还需要用可删堆维护每个节点子树内的点到这个节点的父节点的距离的最大值。这样修改时我们先修改每个节点子树内的点到这个节点的父节点的距离的最大值,然后再修改子树内关灯的节点到这个点的最长和次长路径,最后再修改所有节点的最长路径。上面的修改均需要先撤销原来的贡献再加入新的贡献,在可删堆里删除加入元素即可。
最后特判一下关灯房间数小于等于 \(1\) 的情况,以及每个节点如果关灯,那么需要在这个节点子树内关灯的节点到这个点的最长和次长路径加入一个 \(0\) 表示和这个节点。
#include <bits/stdc++.h>
using namespace std;
struct edge
{
int v,nxt;
}e[200000];
struct heap
{
priority_queue<int>q,del;
void push(int x){q.push(x);}
void erase(int x){del.push(x);}
int top()
{
while(!q.empty()&&!del.empty()&&q.top()==del.top())q.pop(),del.pop();
if(q.empty())return 0;
return q.top();
}
int size(){return q.size()-del.size();}
}s[200000],sf[200000],z;
int n,q,u,v,h[200000],siz[200000],c[200000],del[200000],dfn[200000],vf[200000],st[200000][20],dep[200000],qf[200000],gf[200000],num=0,tn=0,rt=0,dfc=0,cnt=0;
char op;
void add_edge(int u,int v)
{
e[++cnt].nxt=h[u];
e[cnt].v=v;
h[u]=cnt;
}
void findroot(int x,int pr)
{
int mx=0;
siz[x]=1;
for(int i=h[x];i;i=e[i].nxt)
if(e[i].v!=pr&&!del[e[i].v])findroot(e[i].v,x),siz[x]+=siz[e[i].v],mx=max(mx,siz[e[i].v]);
mx=max(mx,tn-siz[x]);
if(mx<=tn/2)rt=x;
}
void dfs(int x,int pr)
{
st[++dfc][0]=pr,dfn[x]=dfc,dep[x]=dep[pr]+1;
for(int i=h[x];i;i=e[i].nxt)
if(e[i].v!=pr)dfs(e[i].v,x);
}
int lca(int x,int y)
{
if(x==y)return x;
int l=dfn[x],r=dfn[y],k=0;
if(l>r)swap(l,r);
l++,k=log2(r-l+1);
if(dfn[st[l][k]]<dfn[st[r-(1<<k)+1][k]])return st[l][k];
return st[r-(1<<k)+1][k];
}
int getdis(int x,int y)
{
return dep[x]+dep[y]-2*dep[lca(x,y)];
}
void calc(int x,int pr)
{
siz[x]=1;
for(int i=h[x];i;i=e[i].nxt)
if(e[i].v!=pr&&!del[e[i].v])calc(e[i].v,x),siz[x]+=siz[e[i].v];
}
void dsu(int x,int pr)
{
del[x]=1;
if(pr)vf[x]=pr;
for(int i=h[x];i;i=e[i].nxt)
if(!del[e[i].v])calc(e[i].v,x),tn=siz[e[i].v],findroot(e[i].v,x),dsu(rt,x);
}
void access(int x)
{
int st=x;
num-=c[st];
if(c[x])s[x].erase(0);
else s[x].push(0);
while(x)
{
if(qf[x])z.erase(qf[x]);
if(s[x].size()>=2)
{
int tmp=qf[x]=s[x].top();
s[x].erase(tmp),qf[x]+=s[x].top(),s[x].push(tmp);
z.push(qf[x]);
}
else qf[x]=0;
if(vf[x])
{
if(gf[x])s[vf[x]].erase(gf[x]);
if(c[st])sf[x].erase(getdis(st,vf[x]));
if(!c[st])sf[x].push(getdis(st,vf[x]));
if(sf[x].size())gf[x]=sf[x].top(),s[vf[x]].push(gf[x]);
else gf[x]=0;
}
x=vf[x];
}
c[st]^=1,num+=c[st];
}
int main()
{
cin>>n;
for(int i=1;i<=n-1;i++)cin>>u>>v,add_edge(u,v),add_edge(v,u);
dfs(1,0),tn=n,findroot(1,0),dsu(rt,0);
for(int j=1;j<=19;j++)
for(int i=1;i+(1<<j)-1<=dfc;i++)
if(dfn[st[i][j-1]]<dfn[st[i+(1<<(j-1))][j-1]])st[i][j]=st[i][j-1];
else st[i][j]=st[i+(1<<(j-1))][j-1];
for(int i=1;i<=n;i++)access(i);
cin>>q;
for(int i=1;i<=q;i++)
{
cin>>op;
if(op=='C')cin>>u,access(u);
else if(op=='G')
{
if(num==0)printf("-1\n");
else if(num==1)printf("0\n");
else printf("%d\n",z.top());
}
}
return 0;
}
例题 \(7\) :
利用点分树寻找关键点的经典题。考虑每次修改后如何求带点权边权的树的重心,考虑从某个点开始,如果有子树权值和 \(\gt\lfloor\frac{n}{2}\rfloor\) 的子树,就走到这棵子树。
但由于树的重心一直在变,所以这个子树权值和并不方便维护。我们考虑点分树可以维护的路径信息,将树的重心转化为到所有点带点权边权的距离。然后根据重心的性质,和上面一样走更优的点就行了。
考虑求某个点到所有点带点权边权的距离。我们通过维护每个点子树内的点到它的距离和到它父亲的距离,暴力跳父节点,通过容斥求出节点的贡献。然后还需要考虑初始点和父节点之间的路径长度的贡献,维护每个点子树内的点权和到它父亲点权,然后容斥求经过这条路径的点的数量乘上去。
但一般树的树高可能很高,因此我们考虑利用点分树寻找关键点技巧,把树高降低至 \(O(\log n)\) 级别。从点分树的根节点开始,每次遍历当前节点的邻节点,如果求出来距离和,就走到那个节点对应的子树的重心,即在点分树上走一条边。
由于每个点的度数有限制,所以时间复杂度为 \(O(nd\log^2 n)\)。当然也可以用 set 维护,时间复杂度 \(O(n\log^3 n)\)。
#include <bits/stdc++.h>
using namespace std;
struct edge
{
int v,w,nxt;
}e[200000];
int n,m,u,v,w,h[200000],siz[200000],del[200000],dfn[200000],vf[200000],st[200000][20],dis[200000],tn=0,rt=0,dfc=0,cnt=0;
long long a[200000],af[200000],sizc[200000],sizf[200000];
vector<int>s[200000],sr[200000];
void add_edge(int u,int v,int w)
{
e[++cnt].nxt=h[u];
e[cnt].v=v;
e[cnt].w=w;
h[u]=cnt;
}
void findroot(int x,int pr)
{
int mx=0;
siz[x]=1;
for(int i=h[x];i;i=e[i].nxt)
if(e[i].v!=pr&&!del[e[i].v])findroot(e[i].v,x),siz[x]+=siz[e[i].v],mx=max(mx,siz[e[i].v]);
mx=max(mx,tn-siz[x]);
if(mx<=tn/2)rt=x;
}
void dfs(int x,int pr,int d)
{
st[++dfc][0]=pr,dfn[x]=dfc,dis[x]=d;
for(int i=h[x];i;i=e[i].nxt)
if(e[i].v!=pr)dfs(e[i].v,x,d+e[i].w);
}
int lca(int x,int y)
{
if(x==y)return x;
int l=dfn[x],r=dfn[y],k=0;
if(l>r)swap(l,r);
l++,k=log2(r-l+1);
if(dfn[st[l][k]]<dfn[st[r-(1<<k)+1][k]])return st[l][k];
return st[r-(1<<k)+1][k];
}
int getdis(int x,int y)
{
return dis[x]+dis[y]-2*dis[lca(x,y)];
}
void calc(int x,int pr)
{
siz[x]=1;
for(int i=h[x];i;i=e[i].nxt)
if(e[i].v!=pr&&!del[e[i].v])calc(e[i].v,x),siz[x]+=siz[e[i].v];
}
void dsu(int x,int pr)
{
del[x]=1;
if(pr)vf[x]=pr;
for(int i=h[x];i;i=e[i].nxt)
if(!del[e[i].v])calc(e[i].v,x),tn=siz[e[i].v],findroot(e[i].v,x),s[x].push_back(e[i].v),sr[x].push_back(rt),dsu(rt,x);
}
void access(int x,int k)
{
int st=x;
while(x)
{
a[x]+=1ll*getdis(st,x)*k,sizc[x]+=k;
if(vf[x])af[x]+=1ll*getdis(st,vf[x])*k,sizf[x]+=k;
x=vf[x];
}
}
long long query(int x)
{
int st=x,t=0;
long long ans=a[x];
while(x)t=x,x=vf[x],ans+=(a[x]-af[t]+(sizc[x]-sizf[t])*getdis(st,x));
return ans;
}
long long move(int x,long long pr)
{
for(int i=0;i<(int)s[x].size();i++)
if(query(s[x][i])<pr)return move(sr[x][i],query(sr[x][i]));
return pr;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n-1;i++)scanf("%d%d%d",&u,&v,&w),add_edge(u,v,w),add_edge(v,u,w);
dfs(1,0,0),tn=n,findroot(1,0),dsu(rt,0);
for(int j=1;j<=19;j++)
for(int i=1;i+(1<<j)-1<=dfc;i++)
if(dfn[st[i][j-1]]<dfn[st[i+(1<<(j-1))][j-1]])st[i][j]=st[i][j-1];
else st[i][j]=st[i+(1<<(j-1))][j-1];
memset(del,0,sizeof(del)),tn=n,findroot(1,0);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&u,&w);
access(u,w);
printf("%lld\n",move(rt,query(rt)));
}
return 0;
}
后记
好累,从身体到心理,一种深深的孤独感与无力感一直笼罩着我。无论我怎么努力,OI 水平无法提高,文化课越来越稀烂。我常常想,另一个世界里,不学竞赛的我,应该会更幸福吧?
回忆无消泯 空留故人叹
南明火未息 徒我拥雪寒
生如星辰璀璨 俯仰天地 凭谁抬头看
千年流光 映夜昙




 浙公网安备 33010602011771号
浙公网安备 33010602011771号