【10】后缀自动机学习笔记
前言
后缀自动机可爱喵!最可爱的后缀类算法!
结论的证明会在结论底下给出,我会尽量证明每一个结论。没给证明一般是我不会证。
Parent Tree
假设我们在对串 \(\text{s}\) 建立 Parent Tree,记 \(\mid \text{s}\mid\) 为字符串 \(\text{s}\) 的长度。
\(\text{endpos}\) 集合:某个子串 \(\text{t}\) 在 \(\text{s}\) 中出现的位置的末尾的集合。
举个例子,若 \(\text{s}=\text{dababcab}\),那 \(\text{t}=\text{ab}\) 的 \(\text{endpos}\) 集合为 \(\{3,5,8\}\)。
性质 \(1\):令 \(\text{t}_1,\text{t}_2\) 是 \(\text{s}\) 的两个子串且 \(\mid \text{t}_1\mid\le\mid \text{t}_2\mid\),\(\text{t}_1\) 是 \(\text{t}_2\) 的后缀当且仅当 \(\text{endpos}(\text{t}_2)\) 是 \(\text{endpos}(\text{t}_1)\) 的子集。
充分性:\(\text{endpos}(\text{t}_2)\) 是 \(\text{endpos}(\text{t}_1)\) 的子集时,出现 \(\text{t}_2\) 的位置一定出现 \(\text{t}_1\),而 \(\text{t}_1\) 长度更短或相同,所以\(\text{t}_1\) 是 \(\text{t}_2\) 的后缀。
必要性:\(\text{t}_1\) 是 \(\text{t}_2\) 的后缀时,\(\text{t}_2\) 出现时 \(\text{t}_1\) 一定出现且 \(\text{endpos}\) 相同,而 \(\text{t}_1\) 可以单独出现,所以 \(\text{endpos}(\text{t}_2)\) 是 \(\text{endpos}(\text{t}_1)\) 的子集。
性质 \(2\):不同子串的 \(\text{endpos}\) 集合要么无交,要么包含。
假设存在相交关系,则证明其中某一个子串是另一个子串的后缀,而由性质 \(1\) 得此时一定是包含关系,矛盾,故原结论成立。
推论 \(1\):\(\text{t}_1\) 不是 \(\text{t}_2\) 的后缀当且仅当 \(\text{endpos}(\text{t}_1)\cap\text{endpos}(\text{t}_2)=\varnothing\)。
考虑性质 \(1\) 的逆否命题,此时这两个 \(\text{endpos}\) 集合不为包含关系,再根据性质 \(2\),此时只能为不交,即 \(\text{endpos}(\text{t}_1)\cap\text{endpos}(\text{t}_2)=\varnothing\)。
等价类:把 \(\text{endpos}\) 集合相同的子串 \(\text{t}\) 的集合称为等价类。
举个例子,若 \(\text{s}=\text{dababcab}\),那 \(\text{t}=\text{ab}\) 的 \(\text{endpos}\) 集合为 \(\{3,5,8\}\),\(\text{t}=\text{b}\) 的 \(\text{endpos}\) 集合也为 \(\{3,5,8\}\),所以子串 \(\text{ab}\) 和 \(\text{b}\) 属于同一个等价类。
在 Parent Tree 上,我们把一个等价类作为一个节点。在每个节点上,我们记 \(\text{maxstr}\) 为这个等价类中最长的字符串,\(\text{minstr}\) 为这个等价类中最短的字符串。
性质 \(3\):一个等价类中,\(\text{maxstr}\) 的任意一个长度大于等于 \(\text{minstr}\) 的后缀 \(\text{t}\) 都属于这个等价类。
根据等价类的定义 \(\text{endpos}(\text{maxstr})=\text{endpos}(\text{minstr})\),故 \(\text{endpos}(\text{maxstr})\) 是 \(\text{endpos}(\text{minstr})\) 的子集。又因为 \(\mid\text{minstr}\mid\le\mid\text{maxstr}\mid\),根据性质 \(1\) 有 \(\text{minstr}\) 是 \(\text{maxstr}\) 的后缀。
又因为 \(\text{t}\) 为 \(\text{maxstr}\) 的后缀且长度大于等于 \(\text{minstr}\),且 \(\text{minstr}\) 是 \(\text{maxstr}\) 的后缀,所以 \(\text{minstr}\) 是 \(\text{t}\) 的后缀,所以 \(\text{endpos}(\text{t})\) 是 \(\text{endpos}(\text{minstr})\) 的子集。又因为又因为 \(\text{t}\) 为 \(\text{maxstr}\) 的后缀,所以 \(\text{endpos}(\text{maxstr})\) 是 \(\text{endpos}(\text{t})\) 的子集。而 \(\text{endpos}(\text{maxstr})=\text{endpos}(\text{minstr})\),所以 \(\text{endpos}(\text{maxstr})=\text{endpos}(\text{minstr})=\text{endpos}(\text{t})\),根据等价类的定义,\(\text{t}\) 属于这个等价类。
推论 \(2\):一个等价类中后缀的长度是连续的,取值范围最小为 \(\mid\text{minstr}\mid\),最大为 \(\mid\text{maxstr}\mid\),且它们均互为后缀关系。
性质 \(3\) 的等价表述。
后缀链接:对于一个等价类 \(\text{a}\),如果我们在其 \(\text{maxstr}\) 前添加某个字符,则这个新字符串属于新的等价类 \(\text{b}\)。这种转化方式叫做后缀链接。
在 Parent Tree 上,我们把 \(\text{a}\) 记为 \(\text{b}\) 在 Parent Tree 上的父亲,记作 \(\text{fa(b)=a}\)。
特别的,Parent Tree 的根节点的等价类包含的字符串有且仅有空串,对应的 \(\text{endpos}\) 集合为 \(\text{s}\) 的每一个位置。
性质 \(4\):\(\mid\text{minstr(b)}\mid=\mid\text{maxstr(a)}\mid+1\)。
根据定义,设 \(\text{t}\) 为 \(\text{maxstr(a)}\) 前面添加一个字符后得到的字符串,有 \(\mid\text{t}\mid=\mid\text{maxstr(a)}\mid+1\) 且 \(\text{maxstr(a)}\) 为 \(\text{t}\) 的后缀。
假设 \(\mid\text{minstr(b)}\mid\lt \text{t}\),则 \(\text{minstr(b)}\) 为 \(\text{t}\) 的后缀,所以 \(\mid\text{minstr(b)}\mid\le\mid\text{maxstr(a)}\mid\),又因为 \(\text{maxstr(a)}\) 为 \(\text{t}\) 的后缀,所以 \(\text{minstr(b)}\) 为 \(\text{maxstr(a)}\) 的后缀,根据性质 \(3\) 得 \(\text{minstr(b)}\) 属于等价类 \(\text{a}\),矛盾,故 \(\mid\text{minstr(b)}\mid\ge \text{t}\)。
又因为取 \(\min\) 运算本身的性质,有 \(\mid\text{minstr(b)}\mid\le \text{t}\),所以 \(\mid\text{minstr(b)}\mid=\mid\text{t}\mid=\mid\text{maxstr(a)}\mid+1\)。同时也能推出 \(\text{minstr(b)=t}\)。
推论 \(3\):等价类 \(\text{a}\) 中任意一个字符串都是等价类 \(\text{b}\) 中任意一个字符串的后缀。
由性质 \(4\) 的过程,\(\text{maxstr(a)}\) 为 \(\text{minstr(b)}\) 的后缀。由推论 \(2\),等价类 \(\text{a}\) 中任意一个字符串都是 \(\text{maxstr(a)}\) 的后缀,\(\text{minstr(b)}\) 是等价类 \(\text{b}\) 中任意一个字符串的后缀,所以该推论成立。
性质 \(5\):一个等价类 \(\text{a}\) 所有后缀链接得到的等价类对应的 \(\text{endpos}\) 互不相交,且得到的等价类对应的 \(\text{endpos}\) 的并集为 \(\text{a}\) 对应的等价类的子集。
对于不同的后缀链接,添加的字符不同,得到的字符串不互为后缀关系。根据推论 \(1\),得到的字符串的 \(\text{endpos}\) 交集为空。根据等价类的定义,所有后缀链接得到的等价类对应的 \(\text{endpos}\) 互不相交。
由推论 \(3\) 和性质 \(1\),后缀链接得到的等价类对应的的 \(\text{endpos}\) 集合一定为等价类 \(\text{a}\) 对应的的 \(\text{endpos}\) 集合的子集,所以并集一定为 \(\text{a}\) 对应的等价类的子集。
性质 \(6\):Parent Tree 点数为 \(O(\mid s\mid)\) 级别。
根据性质 \(5\),考虑最劣情况,每次所有后缀链接对应的 \(\text{endpos}\) 的并集都是这个等价类的 \(\text{endpos}\)。我们可以把 Parent Tree 的某个节点的子节点对应的 \(\text{endpos}\) 看作对这个节点的对应的 \(\text{endpos}\) 的划分。每一次划分至多增加两个节点,而总共至多可以划分 \(\mid\text{s}\mid-1\) 次,所以 Parent Tree 点数为 \(O(\mid \text{s}\mid)\) 级别。
我们来直观地看一下 Parent Tree,这是字符串 \(\text{aababa}\) 的 Parent Tree。
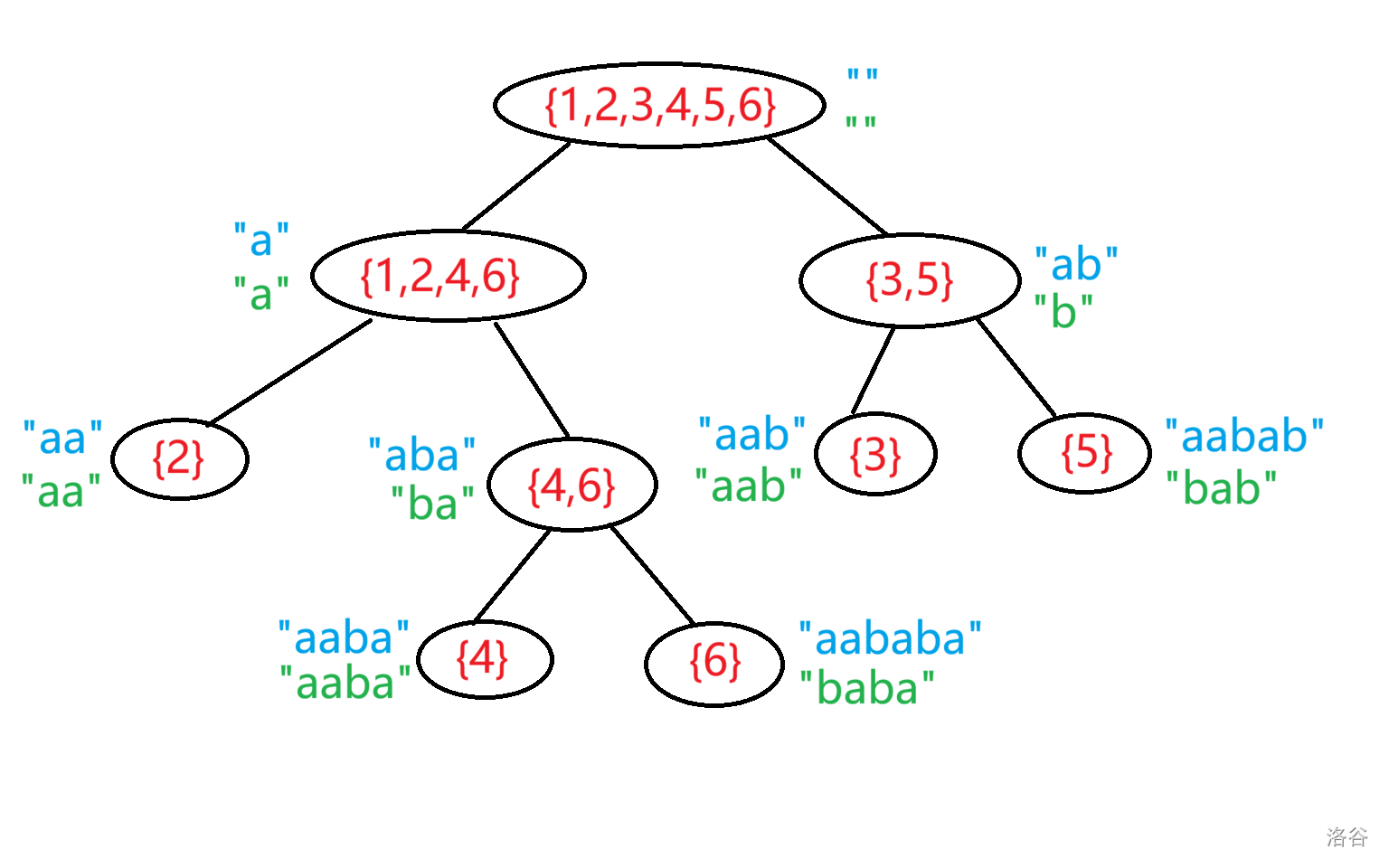
结合上面的推导,我们总结一下 Parent Tree 的直观性质。
\(1\):Parent Tree 是由 \(O(\mid\text{s}\mid)\) 个节点组成的树形结构。
\(2\):Parent Tree 每个节点代表一个 \(\text{endpos}\) 等价类,代表从 \(\text{maxstr}\) 到 \(\text{minstr}\) 中 \(\text{maxstr}\) 的每一个后缀。
\(3\):Parent Tree 从父亲走到儿子相当于在这个父亲等价类的 \(\text{maxstr}\) 前添加一个字符得到儿子等价类的 \(\text{minstr}\),每有一种得到的字符串对应的 \(\text{endpos}\) 等价类不为空的方式,就存在一个子节点。因此 Parent Tree 上包含原串中每一个子串。
\(4\):Parent Tree 中某个节点所有子节点的等价类对应的 \(\text{endpos}\) 集合的并集是这个节点的等价类对应的 \(\text{endpos}\) 集合的子集。
后缀自动机
假设我们在对串 \(\text{s}\) 建立后缀自动机。
后缀自动机:是一个 DAG,每条边的权值是一个字母,满足从起点开始走到任意一个点经过的边上的字母连成的字符串可以得到 \(\text{s}\) 的每一个子串,且不能形成非 \(\text{s}\) 的子串。
因此,后缀自动机上的边相当于在原串后面添加字符。同时,我们也能知道,后缀自动机上的每一条路径和一种子串构成双射。
严格意义上来讲,后缀自动机的定义里还有一条要求是最小的 DAG。但是加上这个限制之后证明非常麻烦,而不加这个其实构造出来的后缀自动机复杂度可以接受,所以我就舍弃了这个限制。
由于 Parent Tree 上包含原串中每一个子串,所以我们考虑在 Parent Tree 上构建后缀自动机。也就是说,后缀自动机的节点就是 Parent Tree 的节点。
接下来考虑构造后缀自动机,我们使用增量构造法,每次在末尾添加一个字符。对于正确性的证明,我们只需要证明在之前的状态满足 Parent Tree 和后缀自动机的性质的情况下,添加后的状态依旧满足 Parent Tree 和后缀自动机的性质的性质即可。
struct node
{
int ch[26],len,fa;
}sam[3000000];
这是后缀自动机的节点定义,这里只记录了构造后缀自动机必须的东西。\(\text{ch}\) 数组表示在末尾添加 \(\text{a}\) 到 \(\text{z}\) 字符时后缀自动机上的边,\(\text{len}\) 表示这个 \(\text{endpos}\) 等价类中的 \(\text{maxstr}\) 的长度,\(\text{fa}\) 表示这个 \(\text{endpos}\) 等价类在 Parent Tree 上的父节点。
int id=c-'a',np=++cnt;
p=las,las=np;
sam[np].len=sam[p].len+1;
现在我们往后缀自动机里添加了第 \(\text{n}\) 个字符 \(\text{c}\)。现在,我们需要把新增的子串插进后缀自动机。这些新子串中最简单的就是整个串,因为它对应的 \(\text{endpos}\) 有且仅有 \(\text{n}\),一定不属于以前任何一个节点,而且一定没有出现过,所以我们新建一个节点 \(\text{np}\) 来保存它。
\(\text{las}\) 记录的是上一次插入时整个串的在后缀自动机上的位置,我们现在让 \(\text{p}\) 指向来这个位置。显然,由于新的整个串就是在原来的整个串上加入了一个字符,且它们都是等价类中的 \(\text{maxstr}\),所以 \(\text{len(np)=len(p)+1}\)。
while(p&&!sam[p].ch[id])sam[p].ch[id]=np,p=sam[p].fa;
然后我们考虑其他的新串。其他新串在添加字符 \(\text{c}\) 之前,一定是上次的整个串的后缀。相当于在前面删字符,所以我们从上一个整个串处跳 Parent Tree 上的 \(\text{fa}\)。
如果某一个上次的整个串的后缀(包括整个串)对应的节点没有 \(\text{c}\) 的出边,证明这个新串没有出现过,\(\text{endpos}\) 与新的整个串相同,属于节点 \(\text{np}\),不需要新建节点。但是由于需要满足后缀自动机可以遍历每一个子串的性质,所以需要连一条边字符 \(\text{c}\) 的边到 \(\text{np}\)。
if(!p)sam[np].fa=1;
这是第一种情况。如果所有 \(\text{fa}\) 都不存在 \(\text{c}\) 的出边,证明新的子串都没有在原串中出现过,\(\text{endpos}\) 都为 \(\{\text{n}\}\),且 Parent Tree 上的父节点只能为根节点,因为其他节点都不包含 \(\text{n}\)。
else
{
int q=sam[p].ch[id];
if(sam[q].len==sam[p].len+1)sam[np].fa=q;
这是第二种情况。如果某一个 \(\text{fa}\) 存在 \(\text{c}\) 的出边,证明新的子串中有一部分已经出现过了。根据 Parent Tree 的性质,继续跳 \(\text{fa}\) 的串加上字符 \(\text{c}\) 也一定出现过了,所以在情况一之前的循环可以截止了。
然后考虑这种情况怎么处理。我们先把 \(\text{c}\) 的出边走到的节点记为 \(\text{q}\)。如果 \(\text{len(q)}\) 恰好等于 \(\text{len(p)+1}\),证明节点 \(\text{q}\) 仅包含新串。因为这是在原串的后缀后面添加了字符 \(\text{c}\),是新串,而这个节点中最长的串是一个新串,节点 \(\text{q}\) 中的节点都是这个串的后缀,又因为新串的后缀都是新串,所以节点 \(\text{q}\) 仅包含新串。且这些新串都是节点 \(\text{np}\) 包含的新串的后缀,为了维护 Parent Tree 的性质,我们令 \(\text{fa(np)=q}\)。
继续跳 \(\text{fa}\) 的串加上字符 \(\text{c}\) 的新串就不用管了,因为后缀自动机性质已满足,而它们由于在 Parent Tree 上是 \(\text{q}\) 的祖先,所以 Parent Tree 的性质也满足了,只不过相当于给这些节点的 \(\text{endpos}\) 都增加了一个元素 \(\text{n}\)。
else
{
int nq=++cnt;
sam[nq].fa=sam[q].fa,sam[nq].len=sam[p].len+1;
for(int i=0;i<26;i++)sam[nq].ch[i]=sam[q].ch[i];
sam[q].fa=sam[np].fa=nq;
这是第三种情况。如果 \(\text{len(q)}\) 不等于 \(\text{len(p)+1}\),则节点 \(\text{q}\) 中一定包含不属于新串的串。因为后缀自动机的边是添加字符,所以 \(\text{len(q)}\) 不会小于 \(\text{len(p)+1}\)。如果长度大于 \(\text{len(p)+1}\) 属于新串,那这个串去掉字符 \(\text{c}\) 后得到的串一定是原来的整个串的后缀,且长度大于 \(\text{len(p)}\)。而 Parent Tree 的走向儿子的边相当于在前面加字符,所以儿子的长度一定比父亲长,又因为得到的串一定是原来的整个串的后缀,所以会在 \(\text{p}\) 之前被跳到,与没跳到的事实矛盾,故一定包含不属于新串的串。
但是,\(\text{q}\) 又一定包含属于新串的串。根据情况二中的讨论,\(\text{q}\) 中长度 \(\le\text{len(p)+1}\) 的串都是新串。此时,新串的 \(\text{endpos}\) 会增加,而非新串不会,因此我们需要分裂这个节点。
我们把新串分裂到 \(\text{nq}\) 节点。根据情况二中的讨论,新串的最长长度为 \(\text{len(p)+1}\),因此 \(\text{len(nq)=len(p)+1}\)。而 \(\text{q}\) 和 \(\text{nq}\) 都属于原来的 \(\text{q}\) 节点,所以原来的 \(\text{q}\) 的出边就是 \(\text{nq}\) 的出边,这是为了维护后缀自动机的性质。
然后,我们维护 Parent Tree 的性质。根据上面分析,\(\text{nq}\) 中的串是 \(\text{q}\) 中的串的后缀,再根据情况二中的分析,这些串也是 \(\text{np}\) 中的串的后缀,所以令 \(\text{fa(q)=fa(np)=nq}\)。
while(p&&sam[p].ch[id]==q)sam[p].ch[id]=nq,p=sam[p].fa;
最后,分裂后不要忘记还有连向本来的节点 \(\text{q}\) 的边。\(\text{p}\) 的祖先加上字符 \(\text{c}\) 之后一定属于新串,如果连向 \(\text{q}\),分裂后应该连向 \(\text{nq}\) 而不是 \(\text{q}\)。
这里如果没有连向 \(\text{q}\) 就可以停止了,因为这样就只会连向 \(\text{q}\) 的祖先,即 \(\text{nq}\) 的祖先。而 \(\text{nq}\) 中全是新串,根据 Parent Tree 的性质,\(\text{q}\) 的祖先也全是新串,已经满足了所有性质。
不知道有没有人和我一样好奇连向 \(\text{q}\) 的边还剩什么,其实还可以由非 \(\text{p}\) 的祖先连后缀自动机的边走到,所以并不破坏性质。
void insert(char c)
{
int id=c-'a',np=++cnt;
p=las,las=np;
sam[np].len=sam[p].len+1;
while(p&&!sam[p].ch[id])sam[p].ch[id]=np,p=sam[p].fa;
if(!p)sam[np].fa=1;
else
{
int q=sam[p].ch[id];
if(sam[q].len==sam[p].len+1)sam[np].fa=q;
else
{
int nq=++cnt;
sam[nq].fa=sam[q].fa,sam[nq].len=sam[p].len+1;
for(int i=0;i<26;i++)sam[nq].ch[i]=sam[q].ch[i];
sam[q].fa=sam[np].fa=nq;
while(p&&sam[p].ch[id]==q)sam[p].ch[id]=nq,p=sam[p].fa;
}
}
}
拼起来,这就是后缀自动机的完整模板。
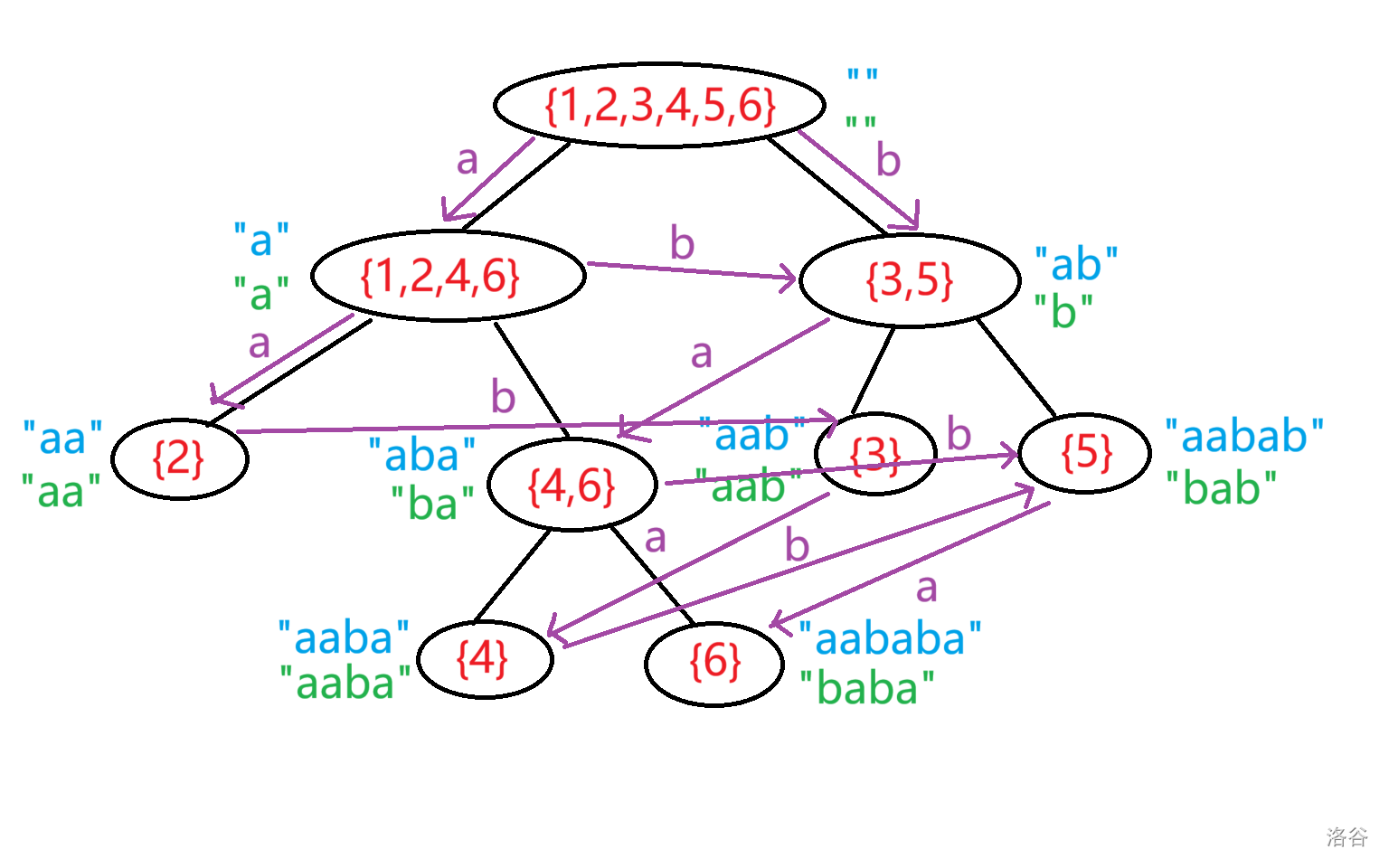
这就是建完之后的后缀自动机了,这里 \(\text{s=aababa}\)。
可以证明后缀自动机的边数为 \(O(\mid\text{s}\mid)\),与字符集大小无关,但是这篇文章中的证明我没有看懂。
但是如果我们知道了后缀自动机的边数为 \(O(\mid\text{s}\mid)\),那我们可以分析出上面的构造方式时间复杂度也是 \(O(\mid\text{s}\mid)\)。因为唯一可能造成复杂度爆炸的是两次 while 循环,而这两次 while 循环都相当于遍历一个新点的所有出边,且新点不会遍历两次,所以相当于把所有边遍历一次,总复杂度是 \(O(\mid\text{s}\mid)\) 的。
注意 Parent Tree 的节点个数有两倍常数,因为可能每个节点都加一个新节点并分裂,所以数组空间要开到两倍 \(\mid\text{s}\mid\)。
后缀自动机的应用可以看例题。
广义后缀自动机
有时我们需要对多个字符串同时分析子串,例如,给定若干个串,统计这些串的所有不重复子串数量。这时我们就需要建立广义后缀自动机。
广义后缀自动机:是一个 DAG,每条边的权值是一个字母,满足从起点开始走到任意一个点经过的边上的字母连成的字符串可以得到字符集 \(\text{S}\) 中每个字符串 \(\text{s}\) 的每一个子串,且不能形成其他子串。
和后缀自动机的定义类似的,广义后缀自动机也有最小性的要求,只是我们如果加上这一点非常不好证,能用就行。
较后缀自动机的构造,广义后缀自动机除了每次插入新串时需要将 \(las\) 清空为最开始的根节点,就只需要在每次插入一个字符时,判断根节点在后缀自动机上是否已经有这个字符的转移边,如果有,就直接使用上面的第二种情况和第三种情况的判断,并将 \(las\) 置为这个字符的转移边连向的节点。需要注意此时没有 \(np\),因此我们直接忽略对 \(np\) 父节点的更新。
正确性不会证,感性理解挺对的。有一个值得注意的点是广义后缀自动机的一个节点可能存储有多个串的信息,需要注意一下。
void insert(int id)
{
if(sam[las].ch[id])
{
int p=las,q=sam[las].ch[id];
if(sam[q].len==sam[p].len+1)las=q;
else
{
int nq=++cnt;
las=nq,sam[nq].fa=sam[q].fa,sam[nq].len=sam[p].len+1,sam[q].fa=nq;
for(int i=0;i<26;i++)sam[nq].ch[i]=sam[q].ch[i];
while(p&&sam[p].ch[id]==q)sam[p].ch[id]=nq,p=sam[p].fa;
}
return;
}
int np=++cnt,p=las;
las=np,sam[np].len=sam[p].len+1;
while(p&&!sam[p].ch[id])sam[p].ch[id]=np,p=sam[p].fa;
if(!p)sam[np].fa=1;
else
{
int q=sam[p].ch[id];
if(sam[q].len==sam[p].len+1)sam[np].fa=q;
else
{
int nq=++cnt;
sam[nq].fa=sam[q].fa,sam[nq].len=sam[p].len+1;
for(int i=0;i<26;i++)sam[nq].ch[i]=sam[q].ch[i];
sam[np].fa=sam[q].fa=nq;
while(p&&sam[p].ch[id]==q)sam[p].ch[id]=nq,p=sam[p].fa;
}
}
}
例题
例题 \(1\) :
子串的出现次数其实就是这个子串对应的 \(\text{endpos}\) 集合大小,我们维护这个就可以了。最后答案就是每个节点的 \(\text{len}\) 乘上 \(\text{endpos}\) 集合大小。
考虑什么情况下某个节点的 \(\text{endpos}\) 集合大小会增加。我们发现,新增的整个串的节点对应的 \(\text{endpos}\) 包含的 \(\{\text{n}\}\),在之前都没有出现过,又因为子节点并集是父节点的子集的性质,因此其所有 Parent Tree 上的祖先 \(\text{endpos}\) 集合大小都会加 \(1\)。且由于不同儿子之间交集为空,所以不存在其他节点 \(\text{endpos}\) 集合大小都会加 \(1\)。
因此,我们给每次新的整个串的节点打上树上差分标记,建完后缀自动机后在 Parent Tree DFS 给需要增加的节点加上。注意分裂时如果被分裂的节点有标记,那么标记应留在分裂后的儿子节点,即留在 \(\text{q}\) 中。\(\text{nq}\) 中不能有标记。
注意读题,出现次数不为 \(1\)。
#include <bits/stdc++.h>
using namespace std;
struct node
{
int ch[26],len,fa,siz;
}sam[3000000];
int n,p=0,las=1,cnt=1;
long long ans=0;
vector<int>t[3000000];
char s[2000000];
void insert(char c)
{
int id=c-'a',np=++cnt;
p=las,las=np;
sam[np].len=sam[p].len+1,sam[np].siz=1;
while(p&&!sam[p].ch[id])sam[p].ch[id]=np,p=sam[p].fa;
if(!p)sam[np].fa=1;
else
{
int q=sam[p].ch[id];
if(sam[q].len==sam[p].len+1)sam[np].fa=q;
else
{
int nq=++cnt;
sam[nq].fa=sam[q].fa,sam[nq].len=sam[p].len+1;
for(int i=0;i<26;i++)sam[nq].ch[i]=sam[q].ch[i];
sam[q].fa=sam[np].fa=nq;
while(p&&sam[p].ch[id]==q)sam[p].ch[id]=nq,p=sam[p].fa;
}
}
}
void dfs(int x)
{
for(int i=0;i<(int)t[x].size();i++)dfs(t[x][i]),sam[x].siz+=sam[t[x][i]].siz;
if(sam[x].siz!=1)ans=max(ans,1ll*sam[x].len*sam[x].siz);
}
int main()
{
scanf("%s",s+1);
n=strlen(s+1);
for(int i=1;i<=n;i++)insert(s[i]);
for(int i=1;i<=cnt;i++)t[sam[i].fa].push_back(i);
dfs(1);
printf("%lld\n",ans);
return 0;
}
例题 \(2\) :
(没找到相关例题,所以就自己出了一个)
给定字符串 \(\text{s}\),有若干次查询,每次给出一个字符串 \(\text{t}\),判断 \(\text{t}\) 是否为 \(\text{s}\) 的子串。如果是子串,还需要求出其出现次数和末尾出现位置。
\(\mid\text{s}\mid\le10^5,\sum\mid\text{t}\mid\le2\times10^6\),保证输出的末尾出现位置的总数 \(k\) 不超过 \(5\times10^5\)。
首先对 \(\text{s}\) 建立后缀自动机。考虑如何查询是否为子串,我们把 \(\text{t}\) 的每个字符在后缀自动机上走路,像 Trie 树一样,每次从当前节点走加入的新字符的边,如果没有边证明不是子串。
查询出现次数例题 \(1\) 已经讲过了,考虑怎么查询末尾出现位置,我们用动态开点线段树记录每个整个串的节点的 \(\text{endpos}\) 集合,然后在 DFS 回溯的过程中利用线段树合并上传,查询时线段树二分就行了。时间复杂度 \(O(\mid\text{s}\mid\log^2\mid\text{s}\mid+\sum\mid\text{t}\mid+k\log\mid\text{s}\mid)\)。
\(\text{endpos}\) 集合除了构建 SAM 的过程中维护,还有一种方式是先建完 SAM 后再逐个插入,每次在走到的点插入对应的 \(\text{ednpos}\),最后再用同样的线段树合并上传。感觉第二个做法更自然一点。
例题 \(3\) :
广义后缀自动机模板题,不多赘述。
#include <bits/stdc++.h>
using namespace std;
struct node
{
int ch[26],len,fa;
}sam[3000000];
int n,las=1,cnt=1;
long long ans=0;
char s[3000000];
void insert(int id)
{
if(sam[las].ch[id])
{
int p=las,q=sam[las].ch[id];
if(sam[q].len==sam[p].len+1)las=q;
else
{
int nq=++cnt;
las=nq,sam[nq].fa=sam[q].fa,sam[nq].len=sam[p].len+1,sam[q].fa=nq;
for(int i=0;i<26;i++)sam[nq].ch[i]=sam[q].ch[i];
while(p&&sam[p].ch[id]==q)sam[p].ch[id]=nq,p=sam[p].fa;
}
return;
}
int np=++cnt,p=las;
las=np,sam[np].len=sam[p].len+1;
while(p&&!sam[p].ch[id])sam[p].ch[id]=np,p=sam[p].fa;
if(!p)sam[np].fa=1;
else
{
int q=sam[p].ch[id];
if(sam[q].len==sam[p].len+1)sam[np].fa=q;
else
{
int nq=++cnt;
sam[nq].fa=sam[q].fa,sam[nq].len=sam[p].len+1;
for(int i=0;i<26;i++)sam[nq].ch[i]=sam[q].ch[i];
sam[np].fa=sam[q].fa=nq;
while(p&&sam[p].ch[id]==q)sam[p].ch[id]=nq,p=sam[p].fa;
}
}
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%s",s+1);
int l=strlen(s+1);
for(int j=1;j<=l;j++)insert(s[j]-'a');
las=1;
}
for(int i=1;i<=cnt;i++)ans+=(sam[i].len-sam[sam[i].fa].len);
printf("%lld\n%d\n",ans,cnt);
return 0;
}
例题 \(4\) :
首先对 \(\text{s}\) 建出后缀自动机。对于子串计数问题,我们一般考虑在后缀自动机上跑 DAG DP。
设 \(f[x]\) 表示以 \(x\) 为起点的本质不同子串数量(即相同子串出现多次算一次),\(g[x]\) 表示以 \(x\) 为起点的子串数量(即相同子串出现多次算多次)。我们知道后缀自动机的路径和字符串 \(\text{s}\) 的本质不同子串构成双射,所以 \(f[x]\) 就是后缀自动机这个 DAG 上的路径数量,很容易写出转移方程。
\(f[x]\) 初始值为 \(1\),因为有空串,也就是在 DAG 上一步都不走。
然后我们考虑 \(g[x]\)。注意到子串的出现次数其实就是这个字串属于的节点对应的 \(\text{endpos}\) 大小,所以我们可以认为每个节点在 DAG 上一步都不走有 \(\text{endpos}\) 大小中走法,这样这个 \(\text{endpos}\) 的子串就相当于被统计了出现次数次。所以,我们把 \(g[x]\) 的初值设为节点的 \(\text{endpos}\) 的大小,然后转移就和 \(f[x]\) 一样了。
然后我们考虑怎么求第 \(k\) 小子串。我们按照字典序遍历所有选择,即先遍历一步都不走的情况,再处理下一个字符是 \(\text{a}\) 的,一个字符是 \(\text{b}\) 的……如果对应选择的子串数大于等于 \(k\),那么第 \(k\) 小子串可以通过这个选择得到,直接做这个选择。否则,将 \(k\) 减去这个子串数,因为这些子串一定不会被是第 \(k\) 小子串且需要得到 \(k\) 在下一个选择中的相对大小,然后遍历下一个选择。
如果选择一步都不走的情况就可以结束了,因为子串已经确定,走字符边的情况还需要继续递归。
最后注意一一下本题中第 \(k\) 小子串
不考虑空串,所以根节点处的空串不能计算,修改一下 \(f[x]\) 和 \(g[x]\) 的初值即可。
#include <bits/stdc++.h>
using namespace std;
struct node
{
int ch[26],len,fa,siz;
}sam[1000000];
int n,l,id,las=1,cnt=1;
long long k,num[2][1000000];
vector<int>sf[1000000];
char s[1000000],t[1000000];
void insert(char c)
{
int id=c-'a',np=++cnt,p=0;
p=las,las=np;
sam[np].len=sam[p].len+1,sam[np].siz=1;
while(p&&sam[p].ch[id]==0)sam[p].ch[id]=np,p=sam[p].fa;
if(!p)sam[np].fa=1;
else
{
int q=sam[p].ch[id];
if(sam[q].len==sam[p].len+1)sam[np].fa=q;
else
{
int nq=++cnt;
sam[nq].len=sam[p].len+1,sam[nq].fa=sam[q].fa;
for(int i=0;i<26;i++)sam[nq].ch[i]=sam[q].ch[i];
sam[q].fa=sam[np].fa=nq;
while(p&&sam[p].ch[id]==q)sam[p].ch[id]=nq,p=sam[p].fa;
}
}
}
void dfs1(int x)
{
for(int i=0;i<(int)sf[x].size();i++)dfs1(sf[x][i]),sam[x].siz+=sam[sf[x][i]].siz;
}
void dfs2(int x)
{
if(num[0][x])return;
if(x!=1)num[0][x]=1,num[1][x]=sam[x].siz;
for(int i=0;i<26;i++)
if(sam[x].ch[i])dfs2(sam[x].ch[i]),num[0][x]+=num[0][sam[x].ch[i]],num[1][x]+=num[1][sam[x].ch[i]];
}
void dfs3(int x,int id,long long k)
{
if(x!=1&&id==0)
{
if(k>1)k--;
else return;
}
else if(x!=1&&id==1)
{
if(k>sam[x].siz)k-=sam[x].siz;
else return;
}
for(int i=0;i<26;i++)
if(sam[x].ch[i]&&k>num[id][sam[x].ch[i]])k-=num[id][sam[x].ch[i]];
else if(sam[x].ch[i])
{
t[++l]='a'+i,dfs3(sam[x].ch[i],id,k);
break;
}
}
int main()
{
scanf("%s%d%lld",s+1,&id,&k);
n=strlen(s+1);
for(int i=1;i<=n;i++)insert(s[i]);
for(int i=1;i<=cnt;i++)sf[sam[i].fa].push_back(i);
dfs1(1),dfs2(1);
if(num[id][1]>=k)dfs3(1,id,k),printf("%s",t+1);
else printf("-1");
return 0;
}
例题 \(5\) :
\(L\) 显然具有单调性,考虑二分 \(L\)。判定是一个区间划分问题,考虑动态规划,设 \(f_i\) 表示在点 \(i\) 后面断开的在文章中的位置的数量。有如下转移方程。
其中 \(\text{mx}_{i}\) 表示以 \(i\) 结尾的前缀的每一个后缀在标准作文库中能匹配的最大长度,这具有连续性,因此可以取区间转移。注意到 \(\text{mx}_i\le\text{mx}_{i-1}+1\),两边同时减 \(i\) 并取负有 \(i-\text{mx}_i\ge(i-1)-\text{mx}_{i-1}\),因此转移的左端点具有单调性,右端点也具有单调性,把转移式子中的 \(i\) 独立出来,可以使用单调队列优化 \(f_j-j\) 进行转移。
接下来,求 \(\text{mx}_i\) 是后缀自动机的经典运用,很多后缀自动机的题目做法与之高度相似。我们逐字符插入待检查的作文,考虑从后缀自动机的根节点开始走。每次找是否有与待检查作文的这个字符相同的转移边,如果有则令长度加 \(1\),走转移边。否则跳 Parent-Tree 上的边,直到存在与待检查作文的这个字符相同的转移边。并令长度为这个节点的 \(\text{len}+1\),走转移边。需要特判跳到根都没要满足要求的边的情况,此时要回到根重新走,并将长度清空。每个位置的 \(\text{mx}_i\) 就是插入这个位置后的长度。
正确性可以由后缀自动机的定义直接得出。复杂度是对的,因为每次跳 Parent-Tree 上的边会让长度至少减 \(1\),而每个位置长度至多加 \(1\),均摊复杂度 \(O(n)\)。
这里没有使用广义 SAM,而是用分隔符切断了每个标准作文用普通 SAM 解决。这样做的代价是后缀链接值域很大,需要使用 map 维护,时间复杂度劣一只 \(\log\)。总复杂度预处理和二分 DP 都是 \(O(n\log n)\)。
#include <bits/stdc++.h>
using namespace std;
struct node
{
int len,fa;
map<int,int>ch;
}sam[3000000];
int n,m,id=1,las=1,cnt=1,mx[2000000],f[2000000],q[2000000],l=1,r=0;
char s[2000000];
void insert(int id)
{
int np=++cnt,p=las;
las=np,sam[np].len=sam[p].len+1;
while(p&&!sam[p].ch[id])sam[p].ch[id]=np,p=sam[p].fa;
if(!p)sam[np].fa=1;
else
{
int q=sam[p].ch[id];
if(sam[q].len==sam[p].len+1)sam[np].fa=q;
else
{
int nq=++cnt;
sam[nq].fa=sam[q].fa,sam[nq].len=sam[p].len+1;
sam[nq].ch=sam[q].ch,sam[q].fa=sam[np].fa=nq;
while(p&&sam[p].ch[id]==q)sam[p].ch[id]=nq,p=sam[p].fa;
}
}
}
void calc(char s[])
{
int l=strlen(s+1),x=1,len=0;
for(int i=1;i<=l;i++)
{
int id=s[i]-'0';
if(sam[x].ch[id])x=sam[x].ch[id],len++;
else
{
while(x&&!sam[x].ch[id])x=sam[x].fa;
if(x)len=sam[x].len+1,x=sam[x].ch[id];
else x=1,len=0;
}
mx[i]=len;
}
}
bool check(char s[],int mid)
{
int n=strlen(s+1),ans=0;
f[0]=0,l=1,r=0;
for(int i=1;i<=n;i++)
{
f[i]=f[i-1];
if(i>=mid)
{
while(l<=r&&f[q[r]]-q[r]<=f[i-mid]-(i-mid))r--;
q[++r]=i-mid;
}
while(l<=r&&q[l]<i-mx[i])l++;
if(l<=r)f[i]=max(f[i],f[q[l]]-q[l]+i);
}
for(int i=1;i<=n;i++)ans=max(ans,f[i]);
return ans*10>=n*9;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
scanf("%s",s+1);
int l=strlen(s+1);
for(int j=1;j<=l;j++)insert(s[j]-'0');
insert(++id);
}
for(int i=1;i<=n;i++)
{
scanf("%s",s+1),calc(s);
int l=0,r=strlen(s+1),ans=0;
while(l<=r)
{
int mid=(l+r)>>1;
if(check(s,mid))ans=mid,l=mid+1;
else r=mid-1;
}
printf("%d\n",ans);
}
return 0;
}
例题 \(6\) :
后缀自动机处理拼合前后缀问题与字符串前加字符匹配的经典应用。
算法 \(1\):建出 \(t\) 串的后缀自动机,对于一个大小为 \(\text{siz}\) 的连通块,我们就有了一个 \(O(\text{siz}^2)\) 的暴力:遍历连通块中的每一个节点,从这个节点开始 DFS,走到每一个节点,同时记录在后缀自动机上的匹配状态。由于是往后加字符,所以我们记录现在在后缀自动机上的点后直接在后缀自动机上走边。利用例题 \(1\) 中的做法可以求出一个节点内的字符串的出现次数,直接累计答案即可。特别的,如果没有边,直接返回。
算法 \(2\):树上路径类问题考虑点分治。由于需要进行路径拼合,所以我们考虑枚举特征字符串每一个位置 \(i\),并处理出 \(\text{pr}[i]\) 和 \(\text{nx}[i]\) 分别表示子树中所有点到根的路径形成的字符串的结尾在 \(i\) 位置的出现次数和子树中根到所有点的路径形成的字符串开头在 \(i\) 的次数,对每个位置两项相乘再加起来就是答案。
注意到 \(\text{nx}[i]\) 等价于在特征字符串的反串上的 \(\text{pr}[m-i+1]\),因此我们只需要求两遍 \(\text{pr}[i]\),第二次在反串上求。
考虑怎么求 \(\text{pr}[i]\)。先假设我们知道一个串 \(\text{s}\) 对应后缀自动机中的哪一个节点,那我们发现它对所有满足 \(i\in\text{endpos}(\text{s})\) 的 \(\text{pr}[i]\) 都有 \(1\) 的贡献,即对这个节点对应的 \(\text{endpos}\) 集合中的位置有贡献。由例题 \(2\) 中的思考,我们发现 \(\text{endpos}(\text{s})\) 包含的每个位置都处于 \(\text{s}\) 对应节点的子树内,且每个位置各对应唯一一个 \(\text{endpos}\) 包含这个位置的节点,满足从这个节点往上所有的节点的 \(\text{endpos}\) 都包含这个位置,即插入完一个位置后的 \(\text{las}\)。因此,我们把每个位置对应到对应的 \(\text{las}\) 节点,处理串 \(\text{s}\) 的贡献时在对应节点打上标记,全部处理完后一遍 DFS 下推累加到所有子节点,位置 \(i\) 对应的 \(\text{las}\) 节点的值就是 \(\text{pr}[i]\)。这是一个扩展性很好的后缀自动机维护位置信息的方式。
接下来考虑快速找出子树中所有点到根的路径形成的字符串在后缀自动机中的节点。还是考虑从父节点走到儿子,这相当于在一个字符串前插入字符,维护匹配状态。在一个字符串前插入字符自然想到 Parent Tree,根据 Parent Tree 的性质,如果一个串在前面插入一个字符后这个串的长度没有超过未插入前这个串对应的节点的 \(\text{len}\),则要么字符不一样失配直接返回,要么依旧处于这个节点继续贡献。字符不一样失配比较好判断,维护 \(\text{endpos}\) 集合内的任意一个位置减去长度就能找出特征字符串中这个位置的字符,比较即可。
如果长度超过了 \(\text{len}\),则我们需要对每个节点维护一个 \(\text{nxt}[i]\) 数组表示超过长度时加入字符 \(i\) 在后缀自动机上会走到哪里。根据 Parent Tree 的性质,这一定是该节点在 Parent Tree 上的一个儿子,否则为空的话失配返回。在预处理时可以查询子节点的任意一个 \(\text{endpos}\) 中的位置减去父节点的 \(\text{len}\) 的位置的字符找到添加的是哪个字符,进而求出 \(\text{nxt}\) 数组。上面两段是后缀自动机维护前插字符匹配的通用方法。
需要注意此时来自同一子树内的贡献会算重,因此对每个子树还需要单独做一遍这个算法去重。由于子树也会做这个算法,对于一个大小为 \(\text{siz}\) 的连通块,时间复杂度 \(O(m+\text{siz})\)。
注意到上面两个算法不齐次,考虑均衡根号分治。依旧是点分治,设阈值为 \(B\),对 \(\text{siz}\le B\) 的连通块做算法 \(1\),\(\text{siz}\gt B\) 的连通块做算法 \(2\)。考虑每分出一个 \(\text{siz}\le B\) 的连通块就不需要继续点分治了,因此复杂度为 \(O(B^2\times\frac{n}{B})=O(nB)\)。考虑分治过程中 \(\text{siz}\gt B\) 的最后一层至多存在 \(\lfloor\frac{n}{B}\rfloor\) 个连通块,而上面每次至少合并两个连通块,至多合并 \(\lfloor\frac{n}{B}\rfloor\) 次,因此总复杂度是 \(O(\frac{n}{B}(m+B))=O(\frac{nm}{B}+n)\)。当 \(B=\sqrt{m}\) 时复杂度均衡为 \(O(n\sqrt{m})\)。实际块长取 \(B=500\) 非常优秀。
需要注意算法 \(2\) 在去重的过程中如果子节点连通块大小 \(\text{siz}\gt B\) 需要使用类似算法 \(1\) 的暴力做法,额外需要先走到根节点再走到其他节点。否则复杂度会退化。
#include <bits/stdc++.h>
using namespace std;
struct edge
{
long long v,nxt;
}e[120000];
long long n,m,k,u,v,h[60000],siz[60000],fa[60000],cnt=0,rt=0,tn=0,ans=0;
bool del[60000];
char s[60000],t[60000];
struct sam
{
struct node
{
long long ch[26],len,fa,siz;
}sam[120000];
long long las=1,cnt=1,b[120000],y[120000],pos[120000],nxt[120000][26];
char ss[60000];
vector<long long>s[120000];
void insert(long long id)
{
long long np=++cnt,p=las;
las=np,sam[np].len=sam[p].len+1,sam[np].siz++,pos[np]=sam[np].len;
while(p&&!sam[p].ch[id])sam[p].ch[id]=np,p=sam[p].fa;
if(!p)sam[np].fa=1;
else
{
long long q=sam[p].ch[id];
if(sam[q].len==sam[p].len+1)sam[np].fa=q;
else
{
long long nq=++cnt;
sam[nq].fa=sam[q].fa,sam[nq].len=sam[p].len+1;
for(int i=0;i<26;i++)sam[nq].ch[i]=sam[q].ch[i];
sam[np].fa=sam[q].fa=nq;
while(p&&sam[p].ch[id]==q)sam[p].ch[id]=nq,p=sam[p].fa;
}
}
}
void build()
{
for(int i=2;i<=cnt;i++)s[sam[i].fa].push_back(i);
}
void dfs(long long x)
{
for(int i=0;i<(int)s[x].size();i++)
{
dfs(s[x][i]);
sam[x].siz+=sam[s[x][i]].siz,pos[x]=pos[s[x][i]],nxt[x][ss[pos[x]-sam[x].len]-'a']=s[x][i];
}
}
void clear(long long x)
{
b[x]=0;
for(int i=0;i<(int)s[x].size();i++)clear(s[x][i]);
}
void pushdown(long long x)
{
for(int i=0;i<(int)s[x].size();i++)b[s[x][i]]+=b[x],pushdown(s[x][i]);
}
}sam1,sam2;
void add_edge(long long u,long long v)
{
e[++cnt].nxt=h[u];
e[cnt].v=v;
h[u]=cnt;
}
void calc(long long x,long long pr,long long now,long long opt)
{
ans+=opt*sam1.sam[now].siz;
for(int i=h[x];i;i=e[i].nxt)
if(!del[e[i].v]&&e[i].v!=pr&&sam1.sam[now].ch[s[e[i].v]-'a'])calc(e[i].v,x,sam1.sam[now].ch[s[e[i].v]-'a'],opt);
}
void bf_solve(long long x,long long pr)
{
if(sam1.sam[1].ch[s[x]-'a'])calc(x,0,sam1.sam[1].ch[s[x]-'a'],1);
for(int i=h[x];i;i=e[i].nxt)
if(!del[e[i].v]&&e[i].v!=pr)bf_solve(e[i].v,x);
}
void findroot(long long x,long long pr)
{
siz[x]=1;
long long mx=0;
for(int i=h[x];i;i=e[i].nxt)
if(!del[e[i].v]&&e[i].v!=pr)findroot(e[i].v,x),siz[x]+=siz[e[i].v],mx=max(mx,siz[e[i].v]);
mx=max(mx,tn-siz[x]);
if(mx<=tn/2)rt=x;
}
void dfs1(long long x,long long pr,long long now1,long long l1,long long now2,long long l2)
{
if(l1<sam1.sam[now1].len)
{
if(sam1.ss[sam1.pos[now1]-l1]!=s[x])now1=0;
else sam1.b[now1]++,l1++;
}
else if(sam1.nxt[now1][s[x]-'a'])now1=sam1.nxt[now1][s[x]-'a'],sam1.b[now1]++,l1++;
else now1=0;
if(l2<sam2.sam[now2].len)
{
if(sam2.ss[sam2.pos[now2]-l2]!=s[x])now2=0;
else sam2.b[now2]++,l2++;
}
else if(sam2.nxt[now2][s[x]-'a'])now2=sam2.nxt[now2][s[x]-'a'],sam2.b[now2]++,l2++;
else now2=0;
siz[x]=1;
for(int i=h[x];i;i=e[i].nxt)
if(!del[e[i].v]&&e[i].v!=pr)dfs1(e[i].v,x,now1,l1,now2,l2),siz[x]+=siz[e[i].v];
}
void access(long long x,long long now)
{
long long prt=0,rt=0;
while(x)
{
if(sam1.sam[now].ch[s[x]-'a'])now=sam1.sam[now].ch[s[x]-'a'];
else return;
prt=rt,rt=x,x=fa[x];
}
if(sam1.sam[now].ch[s[prt]-'a'])now=sam1.sam[now].ch[s[prt]-'a'];
else return;
calc(prt,rt,now,-1);
}
void dfs2(long long x,long long pr)
{
fa[x]=pr,access(x,1);
for(int i=h[x];i;i=e[i].nxt)
if(!del[e[i].v]&&e[i].v!=pr)dfs2(e[i].v,x);
}
void dsu(long long x)
{
del[x]=1;
long long now1=1,l1=0,now2=1,l2=0;
if(l1<sam1.sam[now1].len)sam1.b[now1]++,l1++;
else if(sam1.nxt[now1][s[x]-'a'])now1=sam1.nxt[now1][s[x]-'a'],sam1.b[now1]++,l1++;
else now1=0;
if(l2<sam2.sam[now2].len)sam2.b[now2]++,l2++;
else if(sam2.nxt[now2][s[x]-'a'])now2=sam2.nxt[now2][s[x]-'a'],sam2.b[now2]++,l2++;
else now2=0;
for(int i=h[x];i;i=e[i].nxt)
if(!del[e[i].v])dfs1(e[i].v,x,now1,l1,now2,l2);
sam1.pushdown(1),sam2.pushdown(1);
for(int i=1;i<=m;i++)ans+=sam1.b[sam1.y[i]]*sam2.b[sam2.y[i]];
sam1.clear(1),sam2.clear(1);
for(int i=h[x];i;i=e[i].nxt)
if(!del[e[i].v])
{
if(siz[e[i].v]>k)
{
dfs1(e[i].v,x,now1,l1,now2,l2);
sam1.pushdown(1),sam2.pushdown(1);
for(int i=1;i<=m;i++)ans-=sam1.b[sam1.y[i]]*sam2.b[sam2.y[i]];
sam1.clear(1),sam2.clear(1);
}
else fa[x]=0,dfs2(e[i].v,x);
}
for(int i=h[x];i;i=e[i].nxt)
if(!del[e[i].v])
{
if(siz[e[i].v]<=k)bf_solve(e[i].v,x);
else tn=siz[e[i].v],findroot(e[i].v,x),dsu(e[i].v);
}
}
int main()
{
scanf("%lld%lld",&n,&m);
k=500;
for(int i=1;i<=n-1;i++)scanf("%lld%lld",&u,&v),add_edge(u,v),add_edge(v,u);
scanf("%s%s",s+1,t+1);
for(int i=1;i<=m;i++)sam1.insert(t[i]-'a'),sam1.y[i]=sam1.las,sam1.ss[i]=t[i];
sam1.build(),sam1.dfs(1),reverse(t+1,t+m+1);
for(int i=1;i<=m;i++)sam2.insert(t[i]-'a'),sam2.y[m-i+1]=sam2.las,sam2.ss[i]=t[i];
sam2.build(),sam2.dfs(1);
tn=n,findroot(1,0),dsu(rt);
printf("%lld\n",ans);
return 0;
}
例题 \(7\) :
后缀自动机维护子串排名的经典应用,同时也是利用反串转换 Parent-Tree 和后缀自动机维护的信息的典型应用。
由于权值没有负数,当一个字符串的末尾延长时,这个字符串的权值会增大,而逆序排名会减小。因此对于一个左端点,一定仅存在一个右端点满足条件。这种问题的一个经典技巧是二分找到最右边的一个满足权值减排名小于等于 \(0\) 的位置,判定这个位置是否合法。
接下来只需要考虑判定问题,即查询子串权值和排名作差是否为 \(0\)。子串权值可以前缀和,子串排名考虑后缀自动机。
在正串的后缀自动机上求排名需要在后缀自动机上走路,很难维护,考虑利用反串反转 Parent Tree 和后缀自动机维护的信息。
有一个重要性质是反串的后缀自动机上的节点中的字符串在原串中排名连续。因为同一节点上的字符串相当于前加字符,在原串上是后加,且假设中途存在别的长度为 \(l\),那这个节点一定会在 \(l-1\) 的长度分裂。
因此我们建出反串的后缀自动机,然后考虑预处理出每个节点最长的串的排名。考虑字典序是从前往后,因此我们从前往后按字典序 DFS 后加访问每个子串,就可以直接通过遍历过的点加和求出字典序。这是后加,在反串上是前加,就是走 Parent Tree。利用例题 \(6\) 中的预处理一个节点前加一个字符的方法可以预处理出到每个子结点的边的字符,排序一遍做 DFS 按字典序遍历即可。
查询某个子串的排名的时候,由于我们的信息在 Parent Tree 上,是前加,对应到原串是后加,因此我们找到和例题 \(6\) 一样找到左端点对应的节点,这个节点父节点的 \(\text{endpos}\) 集合一定包含左端点,进而一定包含我们查询的子串。因此我们使用树上倍增找到这个子串在哪个节点,然后根据排名连续,用子串长度与节点内最长子串的差就可以求这个子串在原串中的排名,再求逆序即可。时间复杂度 \(O(n\log^2n)\)。
#include <bits/stdc++.h>
using namespace std;
struct node
{
int ch[26],len,fa;
}sam[600000];
int n,v[300000],sv[300000],y[300000],pos[600000],fa[600000][20],las=1,cnt=1;
long long rk[600000],rn;
vector<pair<int,int> >t[600000],ou;
char s[300000];
void insert(int id,int pl)
{
int np=++cnt,p=las;
las=np,sam[np].len=sam[p].len+1,pos[np]=pl,y[pl]=np;
while(p&&!sam[p].ch[id])sam[p].ch[id]=np,p=sam[p].fa;
if(!p)sam[np].fa=1;
else
{
int q=sam[p].ch[id];
if(sam[q].len==sam[p].len+1)sam[np].fa=q;
else
{
int nq=++cnt;
sam[nq].fa=sam[q].fa,sam[nq].len=sam[p].len+1;
for(int i=0;i<26;i++)sam[nq].ch[i]=sam[q].ch[i];
sam[np].fa=sam[q].fa=nq;
while(p&&sam[p].ch[id]==q)sam[p].ch[id]=nq,p=sam[p].fa;
}
}
}
void dfs1(int x)
{
for(int i=0;i<(int)t[x].size();i++)
{
dfs1(t[x][i].second);
if(!pos[x])pos[x]=pos[t[x][i].second];
}
}
void dfs2(int x)
{
rn+=(sam[x].len-sam[sam[x].fa].len),rk[x]=rn;
fa[x][0]=sam[x].fa;
for(int i=1;i<=19;i++)
if(fa[x][i-1])fa[x][i]=fa[fa[x][i-1]][i-1];
else break;
for(int i=0;i<(int)t[x].size();i++)dfs2(t[x][i].second);
}
long long check(int l,int r)
{
int x=y[l];
for(int i=19;i>=0;i--)
if(fa[x][i]&&sam[fa[x][i]].len>=r-l+1)x=fa[x][i];
return sv[r]-sv[l-1]-(rn-(rk[x]-(sam[x].len-(r-l+1)))+1);
}
int main()
{
scanf("%s",s+1);
n=strlen(s+1);
for(int i=1;i<=n;i++)scanf("%d",&v[i]),sv[i]=sv[i-1]+v[i];
for(int i=n;i>=1;i--)insert(s[i]-'a',i);
for(int i=2;i<=cnt;i++)t[sam[i].fa].push_back(make_pair(0,i));
dfs1(1);
for(int i=1;i<=cnt;i++)t[i].clear();
for(int i=2;i<=cnt;i++)t[sam[i].fa].push_back(make_pair(s[pos[i]+sam[sam[i].fa].len]-'a',i));
for(int i=1;i<=cnt;i++)
if(t[i].size())sort(t[i].begin(),t[i].end());
dfs2(1);
for(int i=1;i<=n;i++)
{
int l=i,r=n,ans=0;
while(l<=r)
{
int mid=(l+r)>>1;
if(check(i,mid)<=0)ans=mid,l=mid+1;
else r=mid-1;
}
if(check(i,ans)==0)ou.push_back(make_pair(i,ans));
}
sort(ou.begin(),ou.end());
printf("%d\n",(int)ou.size());
for(int i=0;i<(int)ou.size();i++)printf("%d %d\n",ou[i].first,ou[i].second);
return 0;
}
后记
集训时间比较紧啊,能抽出大宗时间来记这样一篇大工程已经很不错了。例题显然没有覆盖到后缀自动机的全部应用,以后会慢慢补充。
司仙琴 定八荒 情难思量
三魂遗 哪堪寻 大梦一场
朝可见暮已忘 桃源皎月飞光
心有山海 落星河滚烫




 浙公网安备 33010602011771号
浙公网安备 33010602011771号