【8*】根号分治学习笔记
前言
根号分治是继莫队之后(?)均衡规划思想的又一大体现,这篇学习笔记希望不仅仅是记录根号分治这一经典 trick,更是希望能展示均衡规划思想的广泛运用。
可能有的取等不太严谨,但我觉得应该影响不大。
UPD:好吧,根号分治和均衡思想还是有区分的,是我认知浅薄了。但是顺便记一记均衡规划思想也挺好。
此类知识点大纲中并未涉及,所以【8】是我自己的估计,后带星号表示估计,仅供参考。
根号分治
以下 \(\sqrt{n}\) 无特殊说明默认向下取整。
根号分治的本质一般是均衡思想,常见的表现形式是对于同一个问题有两种做法,对于某个阈值 \(\le\sqrt{n}\) 的部分采用第一个做法,阈值 \(\gt \sqrt{n}\) 的部分采用另一个做法,达到均衡的复杂度 \(O(n\sqrt{n})\)。
当然,根号分治有时是为了得到新的性质。
取模根号分治
考虑把 \(n\) 除以 \(k\) 使用带余除法展开,得到 \(n=pk+r\),其中 \(p=\lfloor\frac{n}{k}\rfloor,r=n\bmod k\)。
观察 \(p,r\),我们发现,当 \(k\le \sqrt{n}\) 时,有 \(r=n\bmod k\lt k=\sqrt{n}\),当 \(k\gt \sqrt{n}\) 时,有 \(p=\lfloor\frac{n}{k}\rfloor\le\lfloor\frac{n}{\sqrt{n}}\rfloor\le\sqrt{n}\)。我们发现,在两种情况下,\(p\) 和 \(r\) 中至少有一个 \(\sqrt{n}\)。
因此,对于 \(k\le \sqrt{n}\) 的我们通过 \(r\) 作为下标或枚举的变量来维护或查询,对于 \(k\gt \sqrt{n}\) 我们通过 \(p\) 作为下标或枚举的变量来维护或查询。若单点维护或查询的复杂度为 \(\text{poly}(n)\),则总复杂度为 \(O(\text{poly}(n)\sqrt n)\)。
这种模型在题目中一般表述为取模或除法的形式,因为展开后带余除法是等价的。
经典应用:例题 \(1,3\)。
频数根号分治
假设有 \(n\) 个数,我们统计每个数出现的次数。不难发现,出现次数 \(\gt \sqrt{n}\) 有 \(\le \sqrt{n}\) 个。这个结论运用非常广泛。
这种问题通常会有两种算法,一种复杂度和出现次数有关,另一种复杂度和总数有关。这时候我们就对出现次数 \(\le \sqrt{n}\) 的数使用第一种算法,对出现次数 \(\gt \sqrt{n}\) 的数使用第二种算法。若第一种算法时间复杂度为 \(\text{poly}_1(k)\),其中 \(k\) 为出现次数,第二种算法时间复杂度为 \(\text{poly}_2(n)\),则总复杂度为 \(O((\text{poly}_1(\sqrt{n})+\text{poly}_2(n))\sqrt{n})\)。
注意上述复杂度分析要求 \(\text{poly}_1(k)\) 要大于等于 \(O(n)\) 的算法,因为分析出的结论需要满足所有 \(\le \sqrt{n}\) 的数出现 \(\sqrt{n}\) 次取到复杂度最大值。否则会有一些比较复杂的取等,需要具体情况具体分析。
或者贡献只与出现次数有关,这时就可以分别维护出现次数 \(\le \sqrt{n}\) 的数和 \(\gt \sqrt{n}\) 的数,前者以出现次数为下标或枚举量,后者直接维护每一个数。
经典应用:例题 \(2,3,5\)。
均衡根号分治
或者叫做法拼合根号分治?其实就是上面两种根号分治的一般化。
我们考虑更一般的情景:我们人为对某个量 \(n\) 设定一个阈值 \(B\),且我们有两个算法,算法 \(1\) 关于 \(n\) 正增长,算法 \(2\) 关于 \(n\) 负增长,这时候,我们可以把这两个做法拼合起来,如果 \(n\le B\) 采用算法 \(1\),如果 \(n\gt B\) 采用算法 \(2\),从而做到复杂度均衡,即两边复杂度相同。毕竟,我们算复杂度的时候要按照最劣的来算。
举个例子,算法 \(1\) 时间复杂度 \(O(B)\),算法 \(2\) 时间复杂度 \(O(\frac{n}{B})\),有 \(B=\frac{n}{B}\),解得 \(B=\sqrt{n}\)。此时如果 \(n\le B\) 采用算法 \(1\),如果 \(n\gt B\) 采用算法 \(2\),时间复杂度即为 \(O(\sqrt{n})\)。这就是经典的根号分治。
再举个例子,算法 \(1\) 时间复杂度 \(O(B\log n)\),算法 \(2\) 时间复杂度 \(O(\frac{n}{B\log n})\),有 \(B\log n=\frac{n}{B\log n}\),解得 \(B=\frac{\sqrt n}{\log n}\),此时复杂度为 \(O(\sqrt{n})\)。
这个技巧还经常被用于数据结构中,例如根号均衡,询问分块,以及调块长等等。
经典应用:例题 \(4,5\)。
大小因数根号分治
对于一个正整数 \(n\),\(\gt\sqrt n\) 的因数至多有 \(1\) 个,这通常会启发出一些很好的性质。
带来新的性质的本质是对于这种因数来说,贡献是独立的,可以分别计算而不会影响到别的 \(\gt\sqrt n\) 的因数,因为这种因数至多含有一个。
例如,对于一些划分类题目,含有某个 \(\gt\sqrt n\) 的因数的数可以作为一个集合整体划分而不需要考虑别的因数的影响,从而实现对复杂度的优化。因此,这种题目通常与因数有关。
因此,这种根号分治优化的本质与前三种不同,前三种是为了均衡复杂度,而这一种是直接优化算法本身。
经典应用:例题 \(6,7\)。
例题
例题 \(1\) :
根号分治经典题。本题讲解中 \(n\) 指序列长度。
先考虑查询。若 \(x\le \sqrt{n}\),则对于每个位置 \(i\bmod x\le \sqrt{n}\),模数数量 \(\le \sqrt{n}\)。 所以我们对整个序列维护一个 \(s[x][y]\),表示模 \(x\) 为 \(y\) 下标的元素之和,时直接输出。
若 \(x\gt \sqrt{n}\),满足条件的 \(i\) 有 \(i\bmod x=y\),这样的数每 \(x\) 个会出现一次,总共有 \(\frac{n}{x}=O(\sqrt{n})\) 个,直接暴力求和即可。
再考虑修改。对于 \(x\gt \sqrt{n}\) 的查询,直接在原序列上改就行了。对于 \(x\le \sqrt{n}\) 的查询,我们把 \(\le \sqrt{n}\) 的模数 \(i\) 都试一遍,枚举这些 \(i\) 并修改 \(s[i][x\bmod i]\) 的值即可。
#include <bits/stdc++.h>
using namespace std;
long long q,op,x,y,s[1010][1010],a[600000];
int main()
{
scanf("%lld",&q);
while(q--)
{
scanf("%lld%lld%lld",&op,&x,&y);
if(op==1)
{
for(int i=1;i<=400;i++)s[i][x%i]+=y;
a[x]+=y;
}
else if(op==2)
{
if(x<=400)printf("%lld\n",s[x][y]);
else
{
long long ans=0;
for(int i=y;i<=500001;i+=x)ans+=a[i];
printf("%lld\n",ans);
}
}
}
return 0;
}
例题 \(2\) :
无向图三元环计数有一个固定的算法,分为三步。
\(1\) :给所有无向边重定向。记录每个点的度数,度数大的点指向度数小的点。如果度数相同,编号小的点指向编号大的点。最后这个图是有向无环图。
\(2\) :打标记。对于图中每一个点 \(u\),将其相邻的点标记可以被 \(u\) 到达。
\(3\) :统计答案。对于图中每一个点 \(u\),遍历其可以相邻的点 \(v\),如果 \(v\) 相邻的点 \(w\) 被标记可以被 \(u\) 到达,那么 \((u,v,w)\) 构成一个三元环。三元环不会被重复计算。
根号分治在这题中是为了证明复杂度。给所有无向边重定向这一步不仅去了重,还保证了时间复杂度,非常巧妙。
首先注意到,每一条边的贡献是其两端度数较小的点的度数。如果两端的点度数都小于等于 \(\sqrt{m}\),这条边贡献 \(\sqrt{m}\)。两端的点度数都大于 \(\sqrt{m}\),显然这样的边个数是 \(O(\sqrt{m})\) 级别的,总共献最坏 \(O(m\sqrt{m})\),均摊每条边 \(\sqrt{m}\)。因此总时间复杂度是 \(O(m\sqrt{m})\) 的。
#include <bits/stdc++.h>
using namespace std;
struct edge
{
int v,nxt;
}e[600000];
int n,m,h[200000],b[200000],ind[200000],u[400000],v[400000],cnt=0,ans=0;
void add_edge(int u,int v)
{
e[++cnt].nxt=h[u];
e[cnt].v=v;
h[u]=cnt;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)scanf("%d%d",&u[i],&v[i]),ind[u[i]]++,ind[v[i]]++;
for(int i=1;i<=m;i++)
if((ind[u[i]]>ind[v[i]])||(ind[u[i]]==ind[v[i]]&&u[i]<v[i]))add_edge(u[i],v[i]);
else add_edge(v[i],u[i]);
for(int i=1;i<=n;i++)
{
for(int j=h[i];j;j=e[j].nxt)b[e[j].v]=i;
for(int j=h[i];j;j=e[j].nxt)
for(int k=h[e[j].v];k;k=e[k].nxt)
if(b[e[k].v]==i)ans++;
}
printf("%d",ans);
return 0;
}
例题 \(3\) :
P5072 [Ynoi Easy Round 2015] 盼君勿忘
首先需要转化贡献体,考虑值域上某个数被计算了多少次。总个数是容易的,正难则反,考虑没有出现这个数的子序列个数。假设长度为 \(len\) 的区间内这个数出现了 \(cnt\) 次,则被计算的次数为 \(2^{len}-2^{len-cnt}\)。
和区间每个数出现次数有关,可以离线,考虑莫队。注意到题目每一个询问模数不同,显然不可以直接维护答案变化。虽然莫队修改有 \(O(n\sqrt{n})\) 次,但是询问只有 \(n\) 次,考虑莫队求出区间每个数出现次数,每次 \(O(\sqrt{n})\) 回答询问。
和每个数出现次数有关,考虑频数根号分治。对于出现次数 \(\gt\sqrt{n}\) 的数,不会超过 \(\sqrt{n}\) 个,我们暴力计算每一个的贡献即可。对于出现次数 \(\le \sqrt{n}\) 的数,因为每个数贡献只与出现次数有关,所以我们记录出现次数相同的数的出现次数,枚举出现次数依次计算贡献。
莫队维护出现次数的时候顺便维护一下 \(\gt\sqrt{n}\) 的数和 \(\le\sqrt{n}\) 的数转化,然后按照上述方式计算。
注意到每次算 \(2\) 的幂次带一个 \(\log\),会被卡,所以我们考虑光速幂技巧。具体的,进行取模根号分治,我们令 \(k=\sqrt{n}\),则带余除法展开 \(2^{x}=2^{pk+r}=(2^k)^{p}\times2^r\)。注意到 \(p,r\) 显然 \(\le\sqrt{n}\),于是我们维护 \(2^k\) 和 \(2\) 的 \(\le\sqrt{n}\) 次幂即可做到 \(O(\sqrt{n})\) 预处理,\(O(1)\) 查询。
时间复杂度 \(O(n\sqrt{n})\),两倍常数,前一半是莫队修改 \(O(n\sqrt{n})\) 次,每次 \(O(1)\),后一半是每次 \(O(\sqrt{n})\) 回答 \(O(n)\) 个询问。
#include <bits/stdc++.h>
using namespace std;
struct ask
{
int l,r,mod,p;
}q[100001];
int n,m,k,a[100001],b[100001],t[100001],ans[100001],f[100001],g[100001],tol=0,l=1,r=0;
long long sum[100001];
unordered_set<int>s;
bool cmp(struct ask a,struct ask b)
{
if((a.l-1)/k!=(b.l-1)/k)return a.l<b.l;
if(((a.l-1)/k+1)&1)return a.r<b.r;
else return a.r>b.r;
}
int power(int x,int mod)
{
return 1ll*f[x/k]*g[x%k]%mod;
}
void add(int x)
{
if(t[x]<=k&&t[x])sum[t[x]]-=b[x];
t[x]++,sum[t[x]]+=b[x];
if(t[x]==k+1)s.insert(x);
}
void del(int x)
{
if(t[x]<=k&&t[x])sum[t[x]]-=b[x];
t[x]--,sum[t[x]]+=b[x];
if(t[x]==k)s.erase(x);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&a[i]),b[i]=a[i];
k=sqrt(n-1)+1,f[0]=g[0]=1,sort(b+1,b+n+1),tol=unique(b+1,b+n+1)-b-1;
for(int i=1;i<=n;i++)a[i]=lower_bound(b+1,b+tol+1,a[i])-b;
for(int i=1;i<=m;i++)scanf("%d%d%d",&q[i].l,&q[i].r,&q[i].mod),q[i].p=i;
sort(q+1,q+m+1,cmp);
for(int i=1;i<=m;i++)
{
while(l>q[i].l)l--,add(a[l]);
while(r<q[i].r)r++,add(a[r]);
while(l<q[i].l)del(a[l]),l++;
while(r>q[i].r)del(a[r]),r--;
for(int j=1;j<k;j++)g[j]=g[j-1]*2%q[i].mod;
f[1]=g[k-1]*2%q[i].mod;
for(int j=2;j<=k;j++)f[j]=1ll*f[1]*f[j-1]%q[i].mod;
int res=0;
for(int j=1;j<=k;j++)res=(res+1ll*sum[j]*(1ll*power(q[i].r-q[i].l+1,q[i].mod)-power(q[i].r-q[i].l+1-j,q[i].mod)+q[i].mod)%q[i].mod)%q[i].mod;
auto it=s.begin();
while(it!=s.end())res=(res+1ll*b[*it]*(1ll*power(q[i].r-q[i].l+1,q[i].mod)-power(q[i].r-q[i].l+1-t[*it],q[i].mod)+q[i].mod)%q[i].mod)%q[i].mod,it++;
ans[q[i].p]=res;
}
for(int i=1;i<=m;i++)printf("%d\n",ans[i]);
return 0;
}
例题 \(4\) :
校内 OJ #547. 我愿相信由你所描述的童话(站外题,提供题面展示)
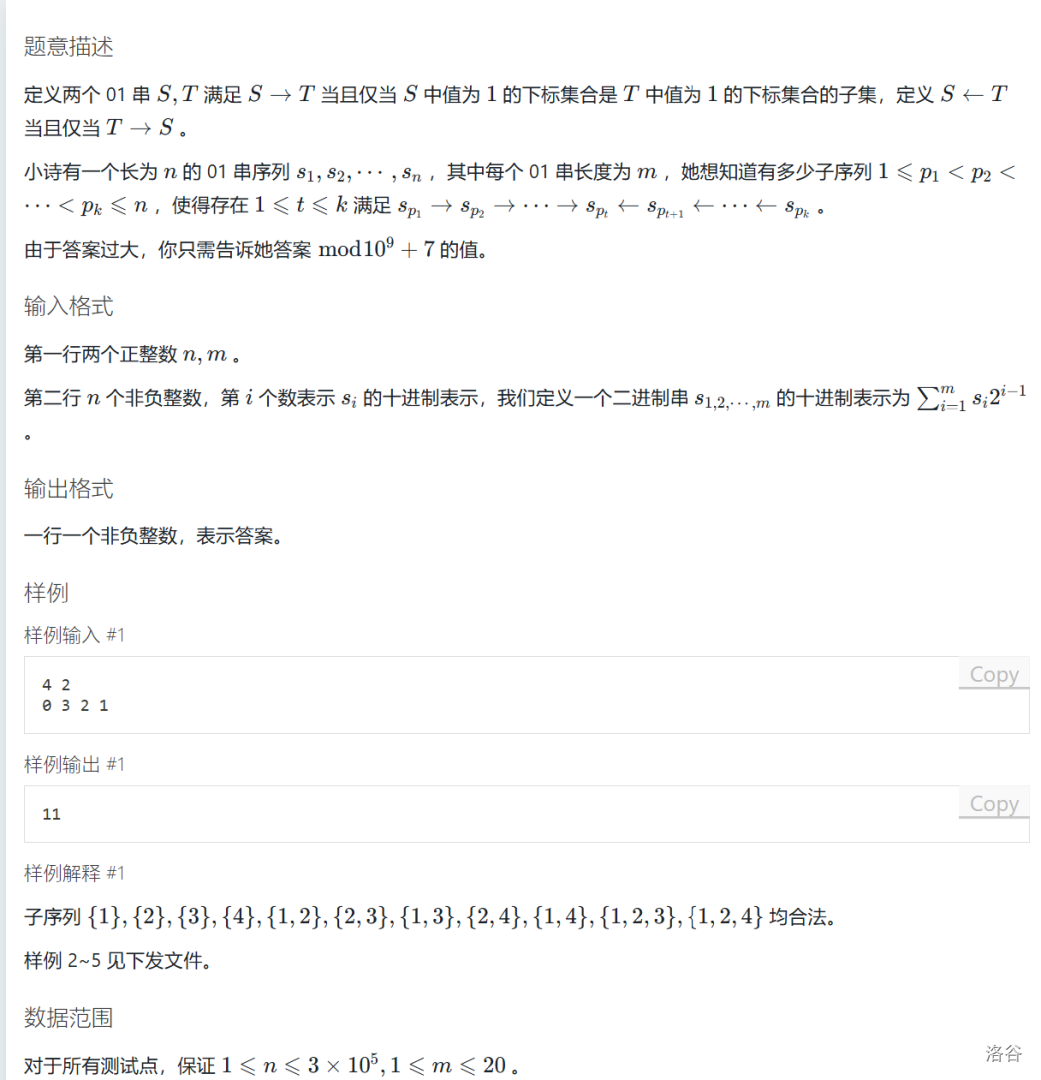
首先考虑朴素 DP,记 \(f_1[x]\) 表示从前往后相邻元素依次满足满足 \(T\to S\),\(f_2[x]\) 表示从后往前相邻元素依次满足满足 \(T\to S\),很容易写出状态转移方程。特别的,令 \(s_0\) 和 \(s_{n+1}\) 为空集。
上式中 \([x]\) 为判断,若 \(x\) 为真则 \([x]=1\),否则 \([x]=0\)。
统计答案的话考虑相加取 \(\max\) 合并 \(f_1\) 和 \(f_2\),但注意到直接合并会在一段连续的相同数字出处算重,因此,我们再记一个 \(f_3\) 强制 \(f_2\) 在最后一步转移时与上一个不同,这样合并的时候第一个出现选择的数位置一定不同,故不会算重。这个 trick 很常用。
然后考虑怎么查。算法 \(1\) 插入枚举超集,查询直接得到答案。算法 \(2\) 直接插入,查询枚举子集。考虑均衡,插入对于低 \(B\) 位枚举超集,对于高 \(B\) 为直接开 \(2^B\) 个桶记录在低 \(B\) 位枚举超集对应的每个数组里。查询对于低 \(B\) 位直接找到对应的桶,然后在这个桶里维护高 \(B\) 位的子集进行查询。对于 \(f_3\) 转移不能相同就另外记一个桶把相同的贡献减去即可。\(B=\log\sqrt{V}\) 时均衡,\(B=10\)。
时间复杂度 \(O(n\sqrt{V})\),空间复杂度 \(O(V)\)。
#include <bits/stdc++.h>
using namespace std;
long long n,m,a[400000],c[400000],f1[400000],f2[400000],f3[400000],s[1100][1100],t[1100000],ans=0;
const long long mod=1e9+7;
void insert(long long x,long long k)
{
for(int i=0;i<(1<<10);i++)
if(((i|(((1<<10)-1)<<10))&x)==x)s[i][x>>10]=(s[i][x>>10]+k)%mod;
}
long long query(long long x)
{
long long ans=0,id=x&((1<<10)-1);
for(int i=0;i<(1<<10);i++)
if((i&(x>>10))==i)ans=(ans+s[id][i])%mod;
return ans;
}
int main()
{
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
for(int i=0;i<=n+1;i++)f1[i]=f2[i]=f3[i]=1;
for(int i=1;i<=n;i++)
f1[i]=(f1[i]+query(a[i]))%mod,insert(a[i],f1[i]);
memset(s,0,sizeof(s));
for(int i=n;i>=1;i--)
f2[i]=(f2[i]+query(a[i]))%mod,insert(a[i],f2[i]);
memset(s,0,sizeof(s));
for(int i=n;i>=1;i--)
f3[i]=((f3[i]+query(a[i]))%mod-t[a[i]]+mod)%mod,insert(a[i],f2[i]),t[a[i]]=(t[a[i]]+f2[i])%mod;
for(int i=1;i<=n;i++)ans=(ans+f1[i]*f3[i]%mod)%mod;
printf("%lld\n",ans);
return 0;
}
例题 \(5\) :
[ICPC 2025 Wuhan]Path Summing Problem(站外题,提供题面翻译)
多测,给定 \(n\times m\) 的矩形,每个位置有颜色,从 \((1,1)\) 出发只能向右或向下走到 \((n,m)\),每条路径的贡献是路径上不同颜色数,求所有路径的贡献和。
\(\sum n\times m\le 10^5\)。
直接做显然不可行,考虑转化贡献体。对于每个位置的数,它有贡献当且仅当走到这个数时没有经过与它相同的数。于是,某个位置的贡献为在它之前没有经过与此位置颜色相同的数走到此位置的路径数乘以这个位置到终点的路径数。
后面一部分好求,直接组合数即可。设需要向下走 \(x\) 次,向右走 \(y\) 次,路径数为 \(C_{x+y}^x\)。
考虑求前一部分,显然可以对某一个颜色的所有位置一起求。设现在正在求不经过 \(c\) 颜色。
算法 \(1\) 考虑容斥。把 \(c\) 颜色所有位置按 \(x\) 第一关键字,\(y\) 第二关键字排好序,设 \(f[i]\) 为钦定排序后第 \(i\) 个位置是第一个经过的 \(c\) 颜色的位置,首先总路径数为 \(C_{x_i,y_i}^{x_i}\)。然后减掉不合法的路径,即枚举 \(j\lt i\) 且满足 \(x_j\le x_i,y_j\le y_i\) 的位置,减掉经过了这个位置的方案数,即 \(f[j]\times C_{x_i-x_j+y_i-y_j}^{x_i-x_j}\),前一部分是 \((1,1)\to(x_j,y_j)\),后一部分是 \((x_j,y_j)\to(x_i,y_i)\)。因为第一个到达的 \(c\) 颜色的位置不同,所以减掉的路径一定不重。设有 \(k\) 个 \(c\) 颜色的位置,时间复杂度 \(O(k^2)\)。
算法 \(2\) 朴素 DP,记 \(f[x][y]\) 为 \((1,1)\to(x,y)\) 不经过 \(c\) 的路径数,从非 \(c\) 颜色的 \((x-1,y)\) 和 \((x,y-1)\) 累加转移。颜色 \(c\) 的位置要求的贡献也从 \((x-1,y)\) 和 \((x,y-1)\) 累加转移,只不过不参与后面的转移。时间复杂度 \(O(mn)\)。
考虑频数根号分治,并进行均衡。出现次数 \(\gt\sqrt n\) 的数至多有 \(\sqrt{n}\) 个,这种数我们直接使用算法 \(2\),这一部分时间复杂度 \(O(\sqrt{n})\)。出现次数 \(\le\sqrt n\) 的数我们使用算法 \(1\),根据频数根号分治中的分析这一部分复杂度为 \(O(n\sqrt{n})\)。总的时间复杂度为 \(O(n\sqrt{n})\)。
#include <bits/stdc++.h>
using namespace std;
long long t,n,m,a[300000],cnt[300000],f[300000],g[300000],jc[300000],inv[300000];
vector<pair<long long,long long> >p[300000];
const long long mod=998244353;
long long has(long long x,long long y)
{
return (x-1)*m+y;
}
long long power(long long a,long long p)
{
long long x=a,ans=1;
while(p)
{
if(p&1)ans=ans*x%mod;
p>>=1;
x=x*x%mod;
}
return ans;
}
long long c(long long n,long long k)
{
return jc[n]*inv[n-k]%mod*inv[k]%mod;
}
int main()
{
scanf("%lld",&t);
jc[0]=1;
for(int i=1;i<=200000;i++)jc[i]=jc[i-1]*i%mod;
inv[200000]=power(jc[200000],mod-2);
for(int i=199999;i>=0;i--)inv[i]=inv[i+1]*(i+1)%mod;
while(t--)
{
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n*m;i++)cnt[i]=0,p[i].clear();
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%lld",&a[has(i,j)]),cnt[a[has(i,j)]]++,p[a[has(i,j)]].push_back({i,j});
long long ans=0;
for(int k=1;k<=n*m;k++)
if(cnt[k]<sqrt(n*m))
{
for(int i=0;i<(int)p[k].size();i++)g[i]=0;
for(int i=0;i<(int)p[k].size();i++)
{
g[i]=c(p[k][i].first-1+p[k][i].second-1,p[k][i].first-1);
for(int j=0;j<i;j++)
if(p[k][j].first<=p[k][i].first&&p[k][j].second<=p[k][i].second)g[i]=(g[i]-g[j]*c(p[k][i].first-p[k][j].first+p[k][i].second-p[k][j].second,p[k][i].first-p[k][j].first)%mod+mod)%mod;
}
for(int i=0;i<(int)p[k].size();i++)ans=(ans+g[i]*c(n-p[k][i].first+m-p[k][i].second,n-p[k][i].first)%mod)%mod;
}
else
{
for(int i=1;i<=n*m;i++)f[i]=0;
f[has(1,1)]=1;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
if(i!=1&&a[has(i-1,j)]!=k)f[has(i,j)]=(f[has(i,j)]+f[has(i-1,j)])%mod;
if(j!=1&&a[has(i,j-1)]!=k)f[has(i,j)]=(f[has(i,j)]+f[has(i,j-1)])%mod;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(a[has(i,j)]==k)ans=(ans+f[has(i,j)]*c(n-i+m-j,n-i)%mod)%mod;
}
printf("%lld\n",ans);
}
return 0;
}
例题 \(6\) :
首先考虑一个显然的状压 DP,记 \(f[x][S_1][S_2]\) 表示考虑到美味度为 \(x\) 的寿司,小 G 已有的质因数集合为 \(S_1\),小 W 已有的质因数集合为 \(S_2\) 的方案数,且 \(S_1\&S_2=\varnothing\)。转移的话考虑预处理出所有 \(x\) 含有的质因数的集合 \(S_x\),如果 \(S_x\) 与 \(S_1\) 没有交集,那么这个寿司就可以分给小 W。反之同理。
可以使用滚动数组优化,时间复杂度 \(O(n2^{2\times\text{n以内的质数个数}})\),显然过不了。
考虑大小因数根号分治。对于 \(\gt\sqrt{n}\) 的大质因数,每个数至多包含一个。因此,我们把拥有同一个大质因数的数(没有则为 \(1\))放到一起转移,不需要考虑其他大质因数的影响。由于拥有同一个大质因数的数只能给小 G 和小 W 中的一人,所以我们分别转移小 G 和小 W 在这些拥有同一个大质因数的数任选的方案数,最后把相同状态,即 \(S_1,S_2\) 相同的状态直接累加合并。注意这会算重,因为这些寿司一个都不选的情况被计算的两次,因此我们还需把转移前 \(f[x][S_1][S_2]\) 的状态记下来,表示一个都不选的情况数,减掉即可。
然后考虑 \(\le\sqrt{n}\) 的小质因数,注意到这种因数并不多,只有 \(7\) 个,所以我们之前的状压 DP 是完全可以使用的。对每个数记录它小质因数的集合 \(S_x\),在转移拥有同一个大质因数的数的时候就可以直接按照之前的方式转移了。时间复杂度 \(O(n2^{14})\),非常优异。
注意对于不包含大质因数的数,也就是代码中认为大质因数为 \(1\) 的数需要单独按照最暴力的方式转移。
代码比较古早,所以滚动数组写得特别唐。
#include <bits/stdc++.h>
using namespace std;
int n,p,id[1000],di[1000],hav[1000],f[2][600][600],f1[600][600],f2[600][600],f3[600][600],ans=0,now=0;
vector<int>b[1000];
void init()
{
id[2]=0,id[3]=1,id[5]=2,id[7]=3,id[11]=4,id[13]=5,id[17]=6,id[19]=7;
di[0]=2,di[1]=3,di[2]=5,di[3]=7,di[4]=11,di[5]=13,di[6]=17,di[7]=19;
for(int i=2;i<=n;i++)
{
int x=i;
for(int j=0;j<=7;j++)
if(x%di[j]==0)
{
hav[i]|=(1<<j);
while(x%di[j]==0)x/=di[j];
}
b[x].push_back(i);
}
}
int main()
{
scanf("%d%d",&n,&p);
init();
f[now][0][0]=1;
for(int i=1;i<=500;i++)
{
if(b[i].empty())continue;
if(i==1)
{
long long l=b[i].size();
for(int ak=0;ak<=511;ak++)
for(int bk=0;bk<=511;bk++)
f1[ak][bk]=f[now][ak][bk];
for(int j=0;j<l;j++)
{
for(int ak=0;ak<=511;ak++)
for(int bk=0;bk<=511;bk++)
{
if(ak&bk)continue;
f[now^1][ak|hav[b[i][j]]][bk]=(f[now^1][ak|hav[b[i][j]]][bk]+f1[ak][bk])%p;
f[now^1][ak][bk|hav[b[i][j]]]=(f[now^1][ak][bk|hav[b[i][j]]]+f1[ak][bk])%p;
f[now^1][ak][bk]=(f[now^1][ak][bk]+f1[ak][bk])%p;
}
if(j!=l-1)
for(int ak=0;ak<=511;ak++)
for(int bk=0;bk<=511;bk++)
f1[ak][bk]=f[now^1][ak][bk],f[now^1][ak][bk]=0;
}
}
else
{
long long l=b[i].size();
for(int ak=0;ak<=511;ak++)
for(int bk=0;bk<=511;bk++)
f1[ak][bk]=f[now][ak][bk],f2[ak][bk]=0;
for(int j=0;j<l;j++)
{
for(int ak=0;ak<=511;ak++)
for(int bk=0;bk<=511;bk++)
{
if(ak&bk)continue;
f2[ak|hav[b[i][j]]][bk]=(f2[ak|hav[b[i][j]]][bk]+f1[ak][bk])%p;
f2[ak][bk]=(f2[ak][bk]+f1[ak][bk])%p;
}
if(j!=l-1)
for(int ak=0;ak<=511;ak++)
for(int bk=0;bk<=511;bk++)
f1[ak][bk]=f2[ak][bk],f2[ak][bk]=0;
}
for(int ak=0;ak<=511;ak++)
for(int bk=0;bk<=511;bk++)
f1[ak][bk]=f[now][ak][bk],f3[ak][bk]=0;
for(int j=0;j<l;j++)
{
for(int ak=0;ak<=511;ak++)
for(int bk=0;bk<=511;bk++)
{
if(ak&bk)continue;
f3[ak][bk|hav[b[i][j]]]=(f3[ak][bk|hav[b[i][j]]]+f1[ak][bk])%p;
f3[ak][bk]=(f3[ak][bk]+f1[ak][bk])%p;
}
if(j!=l-1)
for(int ak=0;ak<=511;ak++)
for(int bk=0;bk<=511;bk++)
f1[ak][bk]=f3[ak][bk],f3[ak][bk]=0;
}
for(int ak=0;ak<=511;ak++)
for(int bk=0;bk<=511;bk++)
f[now^1][ak][bk]=((f2[ak][bk]+f3[ak][bk]-f[now][ak][bk])%p+p)%p;
}
now^=1;
}
for(int i=0;i<=511;i++)
for(int j=0;j<=511;j++)
if(!(i&j))ans=(ans+f[now][i][j])%p;
printf("%d\n",ans);
return 0;
}
例题 \(7\) :
首先注意到值域只有 \(2000\),且每张卡牌顺序可以忽略,所以我们在值域上做,先记录每一个值对应的数的个数。
直接容斥求没办法优化,考虑正难则反。沿用容斥的思想,我们先减掉钦定 \(1\) 个给定的质数没出现,其他给定的质数出不出现随意的情况数,再加上钦定 \(2\) 个质数的情况数,再减掉钦定 \(3\) 个质数的情况数,以此类推,根据容斥原理可以知道这是对的。时间复杂度 \(O(2^{\text{2000以内质数个数}})\),显然过不了。
考虑大小因数根号分治。对于 \(\gt\sqrt{n}\) 的大质因数,每个数至多包含一个。因此,我们把拥有同一个大质因数的数一起考虑。然后,我们考虑 \(\le\sqrt{n}\) 的小质因数,发现这种质因数只有 \(13\) 个,于是我们可以沿用上面的容斥。并且每一个大质因数的数选或不选的方案是独立的,可以直接相乘合并。
因此,我们先枚举对给出的小质因数的容斥状态(即每个小质因数是否出现的状态),再考虑每一个给出的大质因数集合的在该容斥状态下贡献。显然,因为每个大质因数都必须要存在,所以这些数至少要选一个,假设这个大质因数集合有 \(cnt\) 个符合小质因数的容斥状态的数,则方案数为 \(cnt\times2^{cnt-1}\)。
我们可以对于每一个大质因数集合每一个容斥状态预处理出 \(cnt\),这样复杂度为 \(O(2000\times2^{13}+2^{13}\sum c_i)\),可以通过。
#include <bits/stdc++.h>
using namespace std;
long long n,m,q,a[2000000],b[20000],c[20000],t[20000],p[20000],p2[2000000],md[20000],y[20000],f[20000][2001];
const long long mod=998244353;
bool v[20000];
void init(long long mx)
{
v[1]=1,y[2]=0,y[3]=1,y[5]=2,y[7]=3,y[11]=4,y[13]=5,y[17]=6,y[19]=7,y[23]=8,y[29]=9,y[31]=10,y[37]=11,y[41]=12;
for(int i=2;i<=mx;i++)
if(!v[i])for(int j=i*2;j<=mx;j+=i)v[j]=1;
for(int i=1;i<=mx;i++)
{
long long x=i;
for(int j=2;j*j<=x;j++)
if(x%j==0)
{
if(j<=41)p[i]|=(1<<y[j]);
md[i]=max(md[i],1ll*j);
while(x%j==0)x/=j;
}
md[i]=max(md[i],x);
if(x!=1&&x<=41)p[i]|=(1<<y[x]);
}
}
int main()
{
init(2000),p2[0]=1;
for(int i=1;i<=1000000;i++)p2[i]=p2[i-1]*2%mod;
scanf("%lld",&n);
for(int i=1;i<=n;i++)scanf("%lld",&a[i]),b[a[i]]++;
for(int i=0;i<(1<<13);i++)
{
for(int j=2;j<=2000;j++)
{
if(p[j]&i)continue;
f[i][md[j]]+=b[j],t[i]+=b[j];
}
t[i]+=b[1];
}
scanf("%lld",&m);
while(m--)
{
scanf("%lld",&q);
long long mi=0,ans=0;
for(int i=1;i<=q;i++)
{
scanf("%lld",&c[i]);
if(c[i]<=41)mi|=(1<<y[c[i]]);
}
sort(c+1,c+q+1);
for(int i=0;i<(1<<13);i++)
{
if((i|mi)!=mi)continue;
long long cnt=t[i],sum=1,x=i,cp=0;
for(int j=1;j<=q;j++)
if((c[j]>41)&&(j==1||c[j]!=c[j-1]))sum=sum*(p2[f[i][c[j]]]-1)%mod,cnt-=f[i][c[j]];
sum=sum*p2[cnt]%mod;
while(x)cp++,x-=x&(-x);
if(cp&1)ans=((ans-sum)%mod+mod)%mod;
else ans=(ans+sum)%mod;
}
printf("%lld\n",ans);
}
return 0;
}
后记
感觉题目非常杂啊,很多都涉及到的其他知识点。
还有一个趣闻轶事:Kirinosama 老师在讲例题 \(6\) 的时候写了代码,然后调不出来翻车了。于是我们机房所有人每次听到这个题就想起这件事。
昔盘古 开天地 万古穹苍
归墟掩 蟠龙印 遗落星芒
故人立 朝露间 我着浓紫衣裳
见眼底 漾来琥珀光




 浙公网安备 33010602011771号
浙公网安备 33010602011771号