【8】可持久化线段树学习笔记
前言
可持久化线段树,又称为主席树,用于维护静态区间权值信息。例如,在区间 \([l_1,r_1]\) 中查询权值在 \([l_2,r_2]\) 的数的个数。位置区间套权值区间的问题,多使用这个算法。
可持久化线段树
可持久化:数据结构不仅需要维护当前的版本的信息,还需要支持查询之前的历史版本的信息。
为了支持查询历史版本的信息,我们在线段树更新是不能直接在原树上更新,而是应该新建一棵线段树。
我们发现,更新前后两棵树有区别的节点只有更新时用到的 \(\log n\) 个节点,大部分节点都相同。因此,我们只把更新的节点专门记录,未更新的节点直接使用,就做到了 \(O(n\log n)\) 的时间空间复杂度。
具体到代码中,就是当更新一个节点时,先复制上一个版本的这个节点,然后更新这个节点的信息,包括维护的信息,左右儿子等。如果左或者右儿子是更新而新增的节点,则改变这个节点的左右儿子信息。我们按照线段树的方式进行递归更新,更新到的节点都按照这种方式处理。
记录每一个版本的根节点,以某个版本的根节点作为查询时的起始节点,即可查询这一个版本的信息。
void add(int pr,int &now,int p)
{
now=++cnt,tr[now]=tr[pr];
tr[now].v++;
if(tr[now].l==tr[now].r)return;
int mid=(tr[now].l+tr[now].r)/2;
if(p<=mid)add(tr[pr].lc,tr[now].lc,p);
else add(tr[pr].rc,tr[now].rc,p);
}
在实际应用中会有一些不同的写法,但是大同小异,核心是一样的。
这样讲可能有一些抽象,所以给出图片讲解,这里以维护权值 \([l,r]\) 中出现的元素数量为例。
首先,先建立一棵线段树。
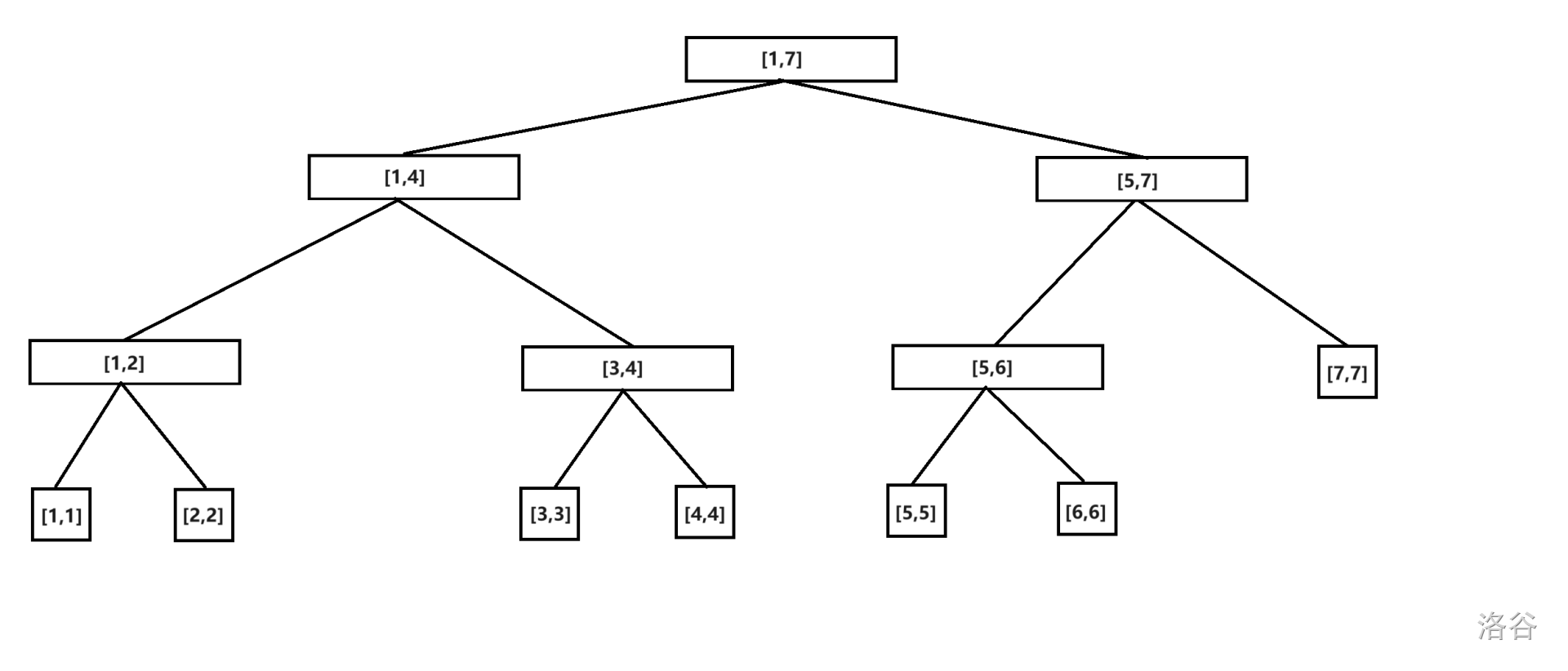
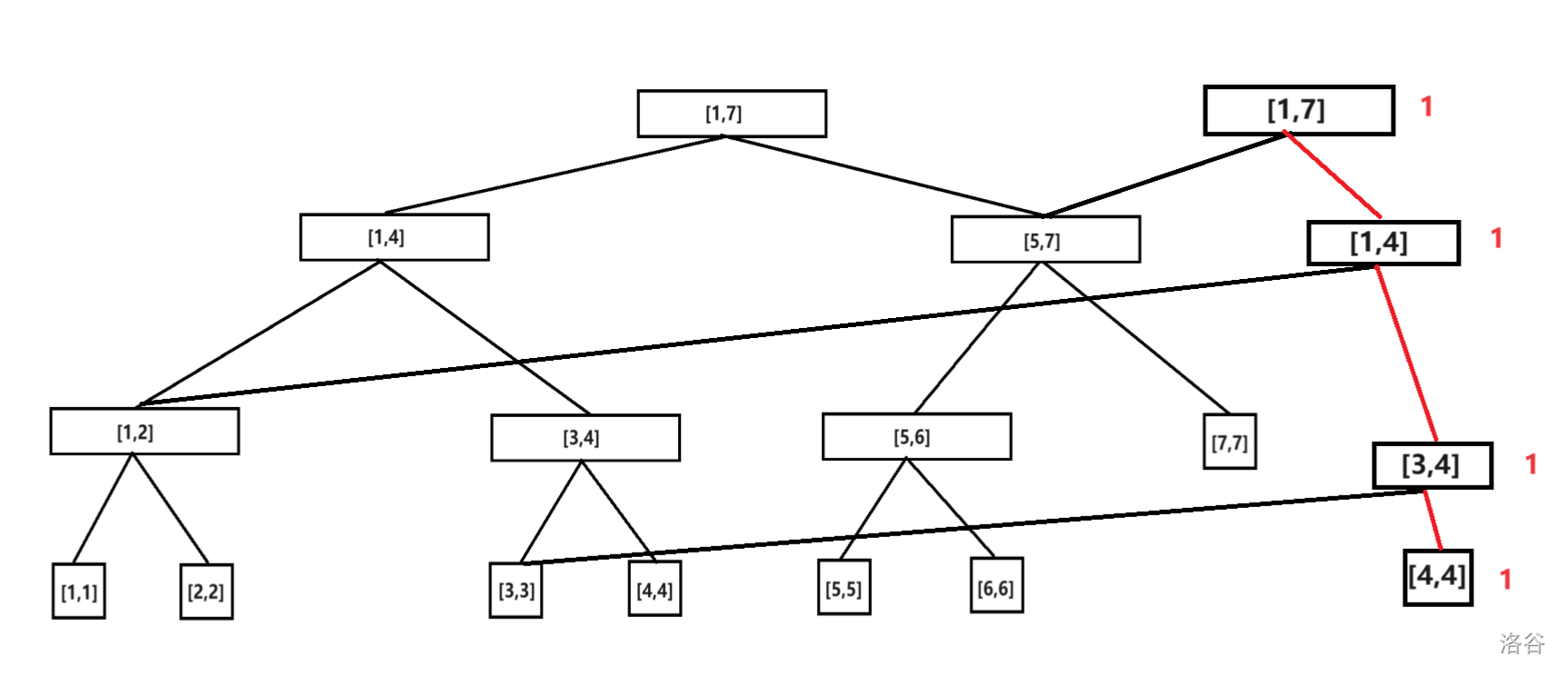
插入数字 \(4\)。节点旁边标红的数字是权值区间内的信息,也就是这个权值区间中出现了多少个元素。没有标注的默认为 \(0\)。
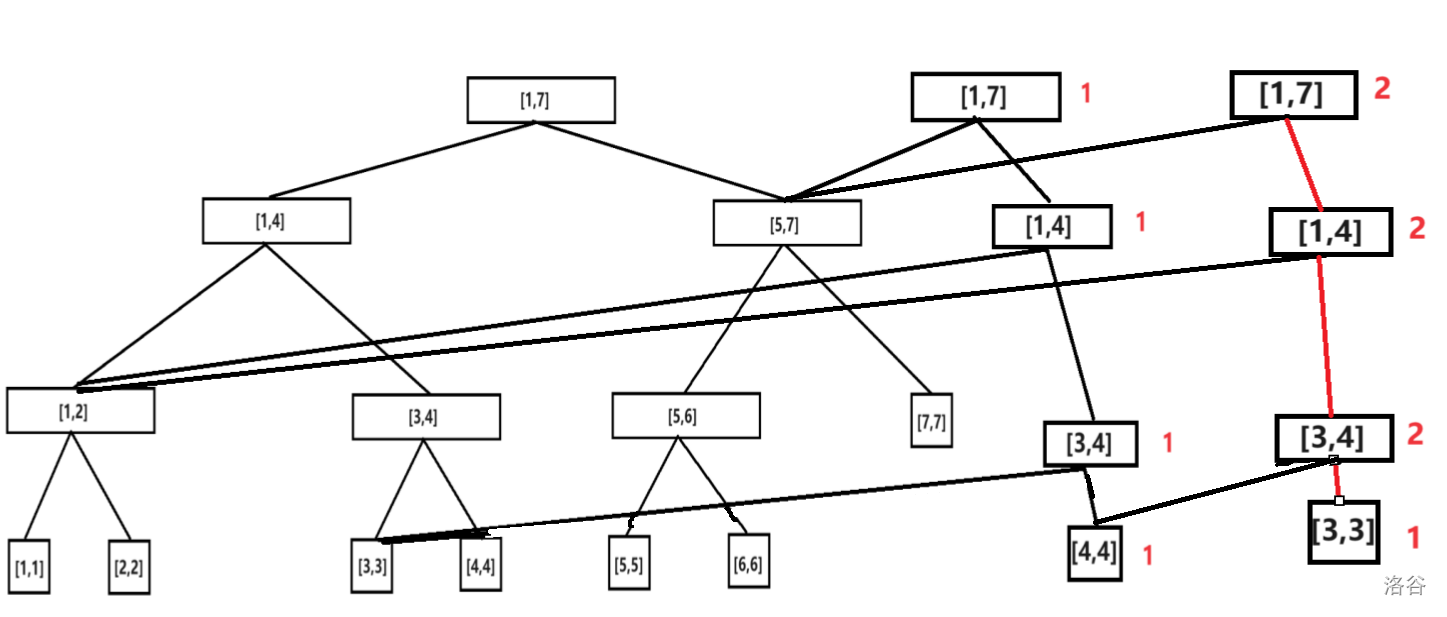
插入数字 \(3\)。
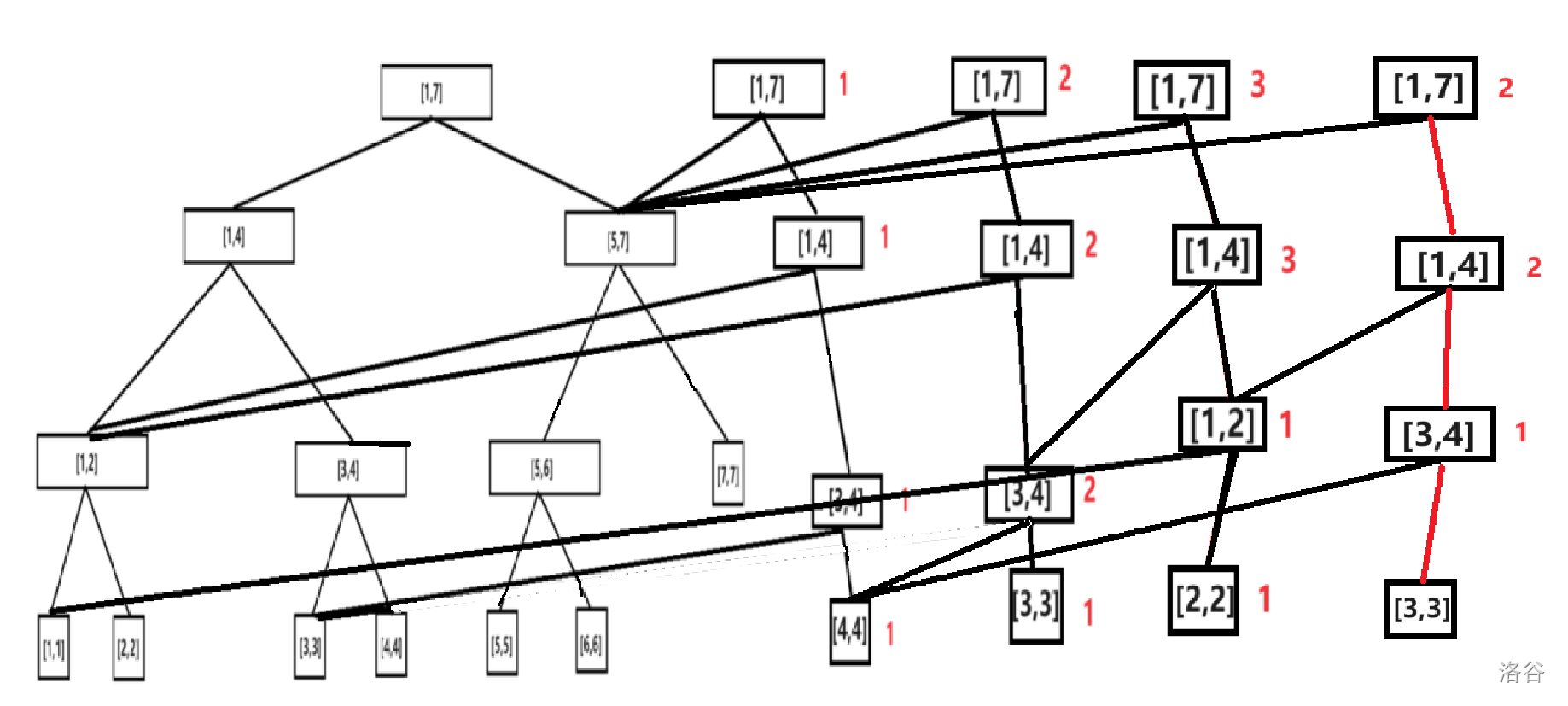
插入数字 \(2\)。

删除数字 \(3\)。
例题
例题 \(1\):
可持久化线段树模板题,节点维护位置区间即可,不多赘述。
#include <bits/stdc++.h>
using namespace std;
struct node
{
int l,r,v,lc,rc;
}tr[50000000];
int n,m,v,op,p,c,a[2000000],root[2000000],cnt=0;
void build(int &now,int l,int r)
{
now=++cnt,tr[now].l=l,tr[now].r=r;
if(l==r)
{
tr[now].v=a[l];
return;
}
build(tr[now].lc,l,(l+r)/2);build(tr[now].rc,(l+r)/2+1,r);
}
void modify(int pr,int &now,int p,int k)
{
now=++cnt;
tr[now]=tr[pr];
if(tr[now].l==tr[now].r)
{
tr[now].v=k;
return;
}
int mid=(tr[now].l+tr[now].r)/2;
if(p<=mid)modify(tr[pr].lc,tr[now].lc,p,k);
else modify(tr[pr].rc,tr[now].rc,p,k);
}
int query(int now,int p)
{
if(tr[now].l==tr[now].r)return tr[now].v;
int mid=(tr[now].l+tr[now].r)/2;
if(p<=mid)return query(tr[now].lc,p);
else return query(tr[now].rc,p);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
build(root[0],1,n);
for(int i=1;i<=m;i++)
{
scanf("%d%d",&v,&op);
if(op==1)
{
scanf("%d%d",&p,&c);
modify(root[v],root[i],p,c);
}
else
{
scanf("%d",&p);
root[i]=root[v];
printf("%d\n",query(root[v],p));
}
}
return 0;
}
例题 \(2\):
由于需要查询区间第 \(k\) 小,我们需要使用权值线段树来维护每个权值内的信息,使用 【6】线段树学习笔记 中提到的方法在 \(O(\log n)\) 的时间内找出第 \(k\) 小。
这是个非常经典的可持久化权值线段树入门题,我们使用一个非常经典的 trick:由于需要维护区间信息,很容易想到前缀和。对于每一个位置,我们建立一棵权值线段树,维护这个前缀中每一个权值范围内出现的数的个数。这样,我们就可以通过两棵权值线段树对应区间权值相减得到这个区间内每个权值区间的数的出现次数,进而求出区间第 \(k\) 小。
我们发现第 \(i+1\) 棵权值线段树可以由第 \(i\) 棵权值线段树进行单点修改得到(\([a_{i+1},a_{i+1}]\) 权值范围内加 \(1\)),这个过程可以使用可持久化。这样既可以访问每一棵权值线段树,也可以节省空间,满足题目要求。
另外,还需要离散化。
#include <bits/stdc++.h>
using namespace std;
struct node
{
int l,r,v,lc,rc;
}tr[4000000];
struct val
{
int v,p;
}d[400000];
int n,m,l,r,k,a[400000],root[400000],y[400000],tol=0,cnt=0;
bool cmp(struct val a,struct val b)
{
return a.v<b.v;
}
void build(int &now,int l,int r)
{
now=++cnt,tr[now].l=l,tr[now].r=r;
if(l==r)return;
build(tr[now].lc,l,(l+r)/2);build(tr[now].rc,(l+r)/2+1,r);
}
void add(int pr,int &now,int p)
{
now=++cnt;
tr[now]=tr[pr];
tr[now].v++;
if(tr[now].l==tr[now].r)return;
int mid=(tr[now].l+tr[now].r)/2;
if(p<=mid)add(tr[pr].lc,tr[now].lc,p);
else add(tr[pr].rc,tr[now].rc,p);
}
int query(int pl,int pr,int k)
{
int num=tr[tr[pr].lc].v-tr[tr[pl].lc].v;
if(tr[pl].l==tr[pl].r)return y[tr[pl].l];
if(k<=num)return query(tr[pl].lc,tr[pr].lc,k);
else return query(tr[pl].rc,tr[pr].rc,k-num);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d",&d[i].v);
d[i].p=i;
}
sort(d+1,d+n+1,cmp);
for(int i=1;i<=n;i++)
{
if(d[i].v!=d[i-1].v||i==1)tol++,y[tol]=d[i].v;
a[d[i].p]=tol;
}
build(root[0],1,tol);
for(int i=1;i<=n;i++)add(root[i-1],root[i],a[i]);
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&l,&r,&k);
printf("%d\n",query(root[l-1],root[r],k));
}
return 0;
}
例题 \(3\):
由于有一次加法运算,所以不可以使用字典树维护,考虑贪心。
我们先忽略那个加法,在区间内找出一个数,使这个数与 \(b_i\) 异或和最大。
首先,我们要使最高位最大。如果 \(b_i\) 的最高位为 \(1\),则我们需要选出的数最高位为 \(0\)。假设最高位为第 \(i\) 位,则需要选出的数最小为 \(0\),最大为 \(2^i-1\)。如果 \(b_i\) 的最高位为 \(0\),则我们需要选出的数最高位为 \(1\)。假设最高位为第 \(i\) 位,则需要选出的数最小为 \(2^i\),最大为 \(2^{i+1}-1\)。当然,如果没有满足最优化条件的数,那么就只能退而求其次了。
我们发现可以选取的数组成了两个区间,\([0,2^i-1]\) 和 \([2^i,2^{i+1}-1]\)。我们只需要维护每个区间内每个权值区间内出现的数的个数,就可以进行查询。我们维护一个变量表示当前已经确定的位数,可以利用这个变量来确定下一位为 \(0\) 或 \(1\) 时的选择范围。一直重复这个过程,直到确定最低位。
这样可以方便地支持那个加法:查询区间变为 \([-x_i,2^i-1-x_i]\) 和 \([2^i-x_i,2^{i+1}-1-x_i]\) 即可。最后,使用主席树维护每个区间内每个权值区间出现的数的个数,就做完了。
#include <bits/stdc++.h>
using namespace std;
struct node
{
long long l,r,v;
}tr[5000000];
long long n,m,b,x,l,r,a[300000],rt[300000],lc[5000000],rc[5000000],cnt=0;
void pushup(long long now)
{
tr[now].v=tr[lc[now]].v+tr[rc[now]].v;
}
void build(long long &now,long long l,long long r)
{
now=++cnt,tr[now].l=l,tr[now].r=r;
if(l==r)return;
long long mid=(l+r)>>1;
build(lc[now],l,mid);
build(rc[now],mid+1,r);
pushup(now);
}
void insert(long long pr,long long &nr,long long p)
{
nr=++cnt,tr[nr]=tr[pr];
lc[nr]=lc[pr],rc[nr]=rc[pr];
if(tr[nr].l==tr[nr].r)
{
tr[nr].v++;
return;
}
long long mid=(tr[nr].l+tr[nr].r)>>1;
if(p<=mid)insert(lc[pr],lc[nr],p);
else if(p>=mid+1)insert(rc[pr],rc[nr],p);
pushup(nr);
}
long long query(long long pr,long long nr,long long l,long long r)
{
long long ans=0;
if(tr[nr].r<l||tr[nr].l>r)return 0;
if(tr[nr].l>=l&&tr[nr].r<=r)return tr[nr].v-tr[pr].v;
long long mid=(tr[nr].l+tr[nr].r)>>1;
if(l<=mid)ans+=query(lc[pr],lc[nr],l,r);
if(r>=mid+1)ans+=query(rc[pr],rc[nr],l,r);
return ans;
}
int main()
{
scanf("%lld%lld",&n,&m);
build(rt[0],-1e5,1e5);
for(int i=1;i<=n;i++)scanf("%lld",&a[i]),insert(rt[i-1],rt[i],a[i]);
for(int i=1;i<=m;i++)
{
scanf("%lld%lld%lld%lld",&b,&x,&l,&r);
long long ans=0;
for(int j=20;j>=0;j--)
{
long long id=(b>>j)&1;
if(id==0&&query(rt[l-1],rt[r],ans+(1<<j)-x,ans+(1<<(j+1))-1-x))ans+=(1<<j);
else if(id==1&&!query(rt[l-1],rt[r],ans-x,ans+(1<<j)-1-x))ans+=(1<<j);
}
printf("%lld\n",ans^b);
}
return 0;
}
例题 \(4\):
我们发现难以直接维护中位数,考虑二分答案。
我们考虑什么样的数有可能成为中位数。假设这个数为 \(x\),我们把大于 \(x\) 的数标记为 \(1\),小于 \(x\) 的数标记为 \(-1\)。我们把标记后的数组称为 \(1,-1\) 数组。一个数在 \([l,r]\) 可以成为中位数,标记后 \([l,r]\) 中的和至少要大于 \(0\)。我们考虑二分每个数,如果存在某个区间内的数之和最大值大于 \(0\),这个数就有可能成为中位数。因为我们调整区间,让区间长度减小,就可以让区间内数的和等于 \(0\)。
特别的,二分出的答案必定在区间中。假设我们当前的答案符合条件但是区间中没有,那么把当前答案增大为区间中出现过的 \(1\) 个更大的数,必定也符合条件,所以最后的答案肯定在区间中出现过。
为了快速求出和最大的区间,我们不仅需要预处理出每一段区间的和,还要预处理出每一段区间的最大前缀和,最大后缀和。询问 \([a,b]\) 和 \([c,d]\) 中最大的一段和就是 \([a,b]\) 中的最大后缀和加上 \([b+1,c-1]\) 的和加上 \([c,d]\) 的最大前缀和。使用 【6】线段树学习笔记 中例题 \(4\) 的处理方式即可。
接下来,我们考虑如何对于每个数预处理出对应的 \(1,-1\) 数组。我们发现从小到大每次数变化时 \(1,-1\) 数组只有一部分会变化,考虑使用可持久化线段树维护。
总的时间复杂度为 \(O(Q\log^2n)\),空间复杂度为 \(O(n\log n)\)。
#include <bits/stdc++.h>
using namespace std;
struct node
{
long long v,rm,lm;
}tr[8000000];
struct val
{
int v,p;
}d[400000];
int n,m,ans=0,zc[400],a[400000],root[400000],lc[400000],rc[400000],cnt=0;
bool cmp(struct val a,struct val b)
{
return a.v<b.v;
}
void decode()
{
for(int i=1;i<=4;i++)zc[i]=(zc[i]+ans)%n,zc[i]++;
sort(zc+1,zc+5);
}
struct node merge(struct node a,struct node b)
{
struct node ans;
ans.v=0,ans.lm=0,ans.rm=0;
ans.v=a.v+b.v;
ans.lm=max(a.lm,a.v+b.lm);
ans.rm=max(b.rm,b.v+a.rm);
return ans;
}
void pushup(long long now)
{
tr[now].v=tr[lc[now]].v+tr[rc[now]].v;
tr[now].lm=max(tr[lc[now]].lm,tr[lc[now]].v+tr[rc[now]].lm);
tr[now].rm=max(tr[rc[now]].rm,tr[rc[now]].v+tr[lc[now]].rm);
}
void build(int &now,int l,int r)
{
now=++cnt;
if(l==r)
{
tr[now].v=tr[now].lm=tr[now].rm=1;
return;
}
build(lc[now],l,(l+r)>>1);
build(rc[now],((l+r)>>1)+1,r);
pushup(now);
}
void add(int pr,int &now,int l,int r,int p)
{
now=++cnt,tr[now]=tr[pr],lc[now]=lc[pr],rc[now]=rc[pr];
if(l==r)
{
tr[now].v=tr[now].lm=tr[now].rm=-1;
return;
}
int mid=(l+r)>>1;
if(p<=mid)add(lc[pr],lc[now],l,mid,p);
else add(rc[pr],rc[now],mid+1,r,p);
pushup(now);
}
struct node query(int now,int l,int r,int lq,int rq)
{
int mid=(l+r)>>1;
if(lq<=l&&rq>=r)return tr[now];
else
{
if(rq<=mid)return query(lc[now],l,mid,lq,rq);
if(lq>=mid+1)return query(rc[now],mid+1,r,lq,rq);
}
return merge(query(lc[now],l,mid,lq,rq),query(rc[now],mid+1,r,lq,rq));
}
int check(int now)
{
int s=0;
struct node ans;
ans.v=0,ans.lm=0,ans.rm=0;
if(zc[2]+1<=zc[3]-1)ans=query(root[now],1,n,zc[2]+1,zc[3]-1);
s+=ans.v;
ans=query(root[now],1,n,zc[1],zc[2]);
s+=ans.rm;
ans=query(root[now],1,n,zc[3],zc[4]);
s+=ans.lm;
return s;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
d[i].v=a[i],d[i].p=i;
}
sort(d+1,d+n+1,cmp);
build(root[1],1,n);
for(int i=2;i<=n;i++)add(root[i-1],root[i],1,n,d[i-1].p);
scanf("%d",&m);
for(int i=1;i<=m;i++)
{
scanf("%d%d%d%d",&zc[1],&zc[2],&zc[3],&zc[4]);
decode();
int l=1,r=n;
ans=0;
while(l<=r)
{
int mid=(l+r)>>1;
if(check(mid)>=0)ans=mid,l=mid+1;
else r=mid-1;
}
ans=d[ans].v;
printf("%d\n",ans);
}
return 0;
}
后记
利用树套树,可持久化线段树甚至可以被用于维护动态区间权值信息。比如这一题:P2617 Dynamic Rankings。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号