【6】树状数组学习笔记
前言
树状数组是我学的第一个高级数据结构,属于 \(\log\) 级数据结构。
其实现在一般不会单独考察数据结构,主要是其在其他算法(如贪心,DP)中起到优化作用。
长文警告:本文一共 \(995\) 行,请合理安排阅读时间。
lowbit函数
lowbit函数用于求解一个数二进制位最右边的 \(1\) 表示的权值,可以使用下面函数计算。
int lowbit(int x)
{
return (x&(-x));
}
举个例子:
树状数组本质上是一个数组,属于线性数据结构。树状数组中,把数按照其 \(lowbit\) 值进行分层,分层虽然没有明显的操作与现象,但导致画出来的层次像树一样,所以叫做树状数组。
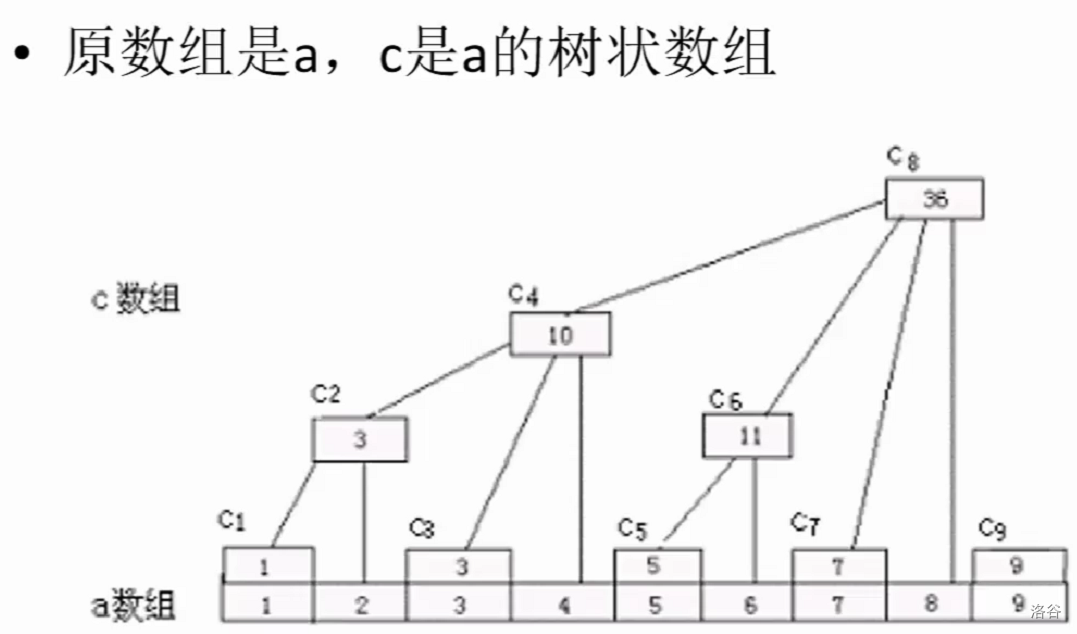
单点修改+区间查询
树状数组支持单点修改,区间查询(一般是求和)。
对于 \(c\) 数组的定义(初始化):
原理类似于倍增,把原数组下标 \(k\) 按照二进制每位进行拆分,通过每个二进制位求出一段区间的和,最后加和得到区间前缀和。
注意:下标从 \(1\) 开始存储。
查询前缀和
使用 \(lowbit\) 求出下标最右边二进制位为 \(1\) 的数位表示的值,然后 \(c\) 数组对应元素累加到结果,再减去这个 \(lowbit\) 值,使之后可以求出下标第二右边二进制位为 \(1\) 的数位表示的值。重复这个过程,直到下标为 \(0\) 。
举个例子:
求 \(a\) 中 \([1,6]\) 的前缀和。
首先,因为 \(6=110,lowbit(6)=2\) ,所以 \(c_6=a_5+a_6\) 。
然后,将最后一位的 \(1\) 减掉,得到 \(4=100,lowbit(4)=4\) ,所以 \(c_4=a_1+a_2+a_3+a_4\) 。
最后,\(c_4+c_6=a_1+a_2+a_3+a_4+a_5+a_6\) ,也就是 \(a\) 中 \([1,6]\) 的前缀和。
正确性证明:
设原下标为 \(k\) ,由 \(lowbit\) 和 \(c\) 数组的定义得求出 \([k-lowbit(k)+1,k]\) 的和。设减去 \(lowbit(k)\) 得 \(l\) ,求出 \([l-lowbit(l)+1,k-lowbit(k)]\) 。观察得这两个区间是相接且不交叉的,可以合并为 \([l-lowbit(l)+1,k]\) ,这样递推下去。由于最后下标为 \(0\) ,故一定可以合并成 \([1,k]\) 。证毕。
int getsum(int x)
{
int t=0;
while(x>0)t+=c[x],x-=lowbit(x);
return t;
}
时间复杂度:\(O(\log n)\)
单点修改
单点修改一个下标后,受影响的必然是减去 \(lowbit\) 后是这个下标,所以可以把 \(lowbit\) 加回来,同时把 \(c\) 数组增加。当然,如果超过了数组元素个数 \(n\) 就没必要再加了。
void add(int x,int d)
{
while(x<=n)c[x]+=d,x+=lowbit(x);
}
时间复杂度:\(O(\log n)\)
初始化
不需要按照 \(c\) 数组的定义来,可以把每一个数都进行一次单点修改操作。
void init()
{
for(int i=1;i<=n;i++)add(i,a[i]);
}
时间复杂度:\(O(n\log n)\)
区间求和
使用查询前缀和查询出前缀和,然后相减就是区间的和。
int ask(int x,int y)
{
return getsum(y)-getsum(x-1);
}
时间复杂度:\(O(\log n)\)
单点修改+区间查询例题
例题 \(1\) :
单点修改+区间查询模板题,不多赘述。
#include <bits/stdc++.h>
using namespace std;
int n,m,a[600000],c[600000];
int lowbit(int x)
{
return (x&(-x));
}
void add(int x,int d)
{
while(x<=n)c[x]+=d,x+=lowbit(x);
}
void init()
{
for(int i=1;i<=n;i++)add(i,a[i]);
}
int getsum(int x)
{
int t=0;
while(x>0)t+=c[x],x-=lowbit(x);
return t;
}
int ask(int x,int y)
{
return getsum(y)-getsum(x-1);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
init();
for(int i=0;i<m;i++)
{
int op,x,y;
scanf("%d%d%d",&op,&x,&y);
if(op==1)add(x,y);
else if(op==2)printf("%d\n",ask(x,y));
}
return 0;
}
例题 \(2\) :
类似例题 \(1\) ,但是不用初始化,注意字符的输入。
#include <bits/stdc++.h>
using namespace std;
long long n,m,a[600000],c[600000];
long long lowbit(long long x)
{
return (x&(-x));
}
void add(long long x,long long d)
{
while(x<=n)c[x]+=d,x+=lowbit(x);
}
long long getsum(long long x)
{
long long t=0;
while(x>0)t+=c[x],x-=lowbit(x);
return t;
}
long long ask(long long x,long long y)
{
return getsum(y)-getsum(x-1);
}
int main()
{
cin>>n>>m;
for(int i=0;i<m;i++)
{
char op;
int x,y;
cin>>op>>x>>y;
if(op=='x')add(x,y);
else if(op=='y')printf("%lld\n",ask(x,y));
}
return 0;
}
例题 \(3\) :
P2982 [USACO10FEB]Slowing down G
树上树状数组。
由于每次每头牛走完之后会单点修改一个值,而放慢速度的次数又取决于从根到目标节点的区间和,自然联想到树状数组。
首先预处理出每个节点的层次,一方面方便遍历树,另一方面方便树上树状数组。
对于单点修改的操作,考虑预处理出修改每个节点之后会影响的点,可以通过先搜索层次深的节点,搜索更浅的节点时记忆化,做到将近 \(O(n\log n)\) 的复杂度。
对于区间查询的操作,考虑预处理出查询每个节点之前会计算的点,可以通过先搜索层次浅的节点,搜索更深的节点时记忆化,同样做到将近 \(O(n\log n)\) 的复杂度。
然后,由于已经预处理了每个点的影响与计算,所以树状数组操作时只需要遍历这些预处理的记录就行了。
注意一定要记忆化,否则很容易退化回 \(O(n^2)\) 。
#include <bits/stdc++.h>
#define lowbit(x) (x&(-x))
using namespace std;
struct edge
{
int to,next;
}e[300000];
struct order
{
int p,c;
}xu[100001];
struct node
{
int b;
vector<int>low;
vector<int>high;
}retree[100001];
int n,h[100001],tol=0,c[100001],book[100001];
inline int read()
{
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
bool cmp(struct order a,struct order b)
{
return a.c>b.c;
}
void add_edge(int u,int v)
{
e[++tol].next=h[u];
e[tol].to=v;
h[u]=tol;
}
void dfs1(int root,int ce)
{
retree[root].b=ce;
for(register int i=h[root];i;i=e[i].next)
{
if(book[e[i].to])continue;
book[e[i].to]=1;
dfs1(e[i].to,ce+1);
}
}
void dfs2(int root,int from,int want)
{
if(retree[root].b==want)
{
int l=retree[root].low.size();
for(int i=0;i<l;i++)retree[from].low.push_back(retree[root].low[i]);
return;
}
if(want>n)return;
for(register int i=h[root];i;i=e[i].next)
{
if(retree[e[i].to].b<=retree[root].b)continue;
dfs2(e[i].to,from,want);
}
}
void dfs3(int root,int from,int want)
{
if(retree[root].b==want)
{
int l=retree[root].high.size();
for(int i=0;i<l;i++)retree[from].high.push_back(retree[root].high[i]);
want-=lowbit(want);
return;
}
if(want<=0)return;
for(register int i=h[root];i;i=e[i].next)
{
if(retree[e[i].to].b>=retree[root].b)continue;
dfs3(e[i].to,from,want);
}
}
void add(int x)
{
int l=retree[x].low.size();
for(register int i=0;i<l;i++)c[retree[x].low[i]]++;
}
int query(int x)
{
int t=0,l=retree[x].high.size();
for(register int i=0;i<l;i++)
t+=c[retree[x].high[i]];
return t;
}
int main()
{
n=read();
for(register int i=0;i<n-1;i++)
{
int u,v;
u=read();v=read();
add_edge(u,v);
add_edge(v,u);
}
for(register int i=1;i<=n;i++)
{
retree[i].low.push_back(i);
retree[i].high.push_back(i);
}
book[1]=1;
dfs1(1,1);
for(register int i=1;i<=n;i++)
xu[i].p=i,xu[i].c=retree[i].b;
sort(xu+1,xu+n+1,cmp);
for(register int i=1;i<=n;i++)dfs2(xu[i].p,xu[i].p,retree[xu[i].p].b+lowbit(retree[xu[i].p].b));
for(register int i=n;i>=1;i--)dfs3(xu[i].p,xu[i].p,retree[xu[i].p].b-lowbit(retree[xu[i].p].b));
for(register int i=1;i<=n;i++)
{
int p;
p=read();
printf("%d\n",query(p));
add(p);
}
return 0;
}
当然,每次修改时计算也是可以的,而且可以大大减少码量,这里不多赘述。
例题 \(4\) :
由于权值值域很小( \(c\le100\) ),可以对每一种权值建立一个二维树状数组,每次更新时单独更新。一个某种权值的格子会对这种权值的答案造成 \(1\) 的贡献,所以可以把每个这种权值的格子视为 \(1\) ,其他的格子视为 \(0\) 。统计个数时加起来就行了。
操作 \(1\) 的处理:
首先,如果把 \(a\) 修改成 \(b\) ,那么会影响 \(a\) 和 \(b\) 两种权值的二维树状数组。可以把 \(a\) 的树状数组影响到的值都加 \(1\) ,而 \(b\) 的树状数组影响到的值都减 \(1\) ,从而达到修改的目的。
对于影响到的值,可以参考一维树状数组的解决方式。将横坐标与纵坐标分别加上其 \(lowbit\) ,把原区间划分为四个小区间。
void add(int x,int y,int k,int s)
{
int i=x,j=y;
while(x<=n)
{
y=j;
while(y<=m)c[x][y][s]+=k,y+=lowbit(y);
x+=lowbit(x);
}
}
void insert()
{
int x=0,y=0,c=0;
scanf("%d%d%d",&x,&y,&c);
add(x,y,1,c);
add(x,y,-1,a[x][y]);
a[x][y]=c;
}
操作 \(2\) 的处理:
设 \(s[i][j]\) 表示二维右下点为 \((i,j)\) 的矩形的前缀和,利用容斥原理得到矩形 \((x_1,y_1,x_2,y_2)\) 的加和值为:
对于前缀和的处理,可以参考一维树状数组的解决方式。将横坐标与纵坐标分别减去其 \(lowbit\) ,把原区间划分为四个小区间。
int getsum(int x,int y,int k)
{
int t=0,i=x,j=y;
while(x>0)
{
y=j;
while(y>0)t+=c[x][y][k],y-=lowbit(y);
x-=lowbit(x);
}
return t;
}
int query()
{
int x1,y1,x2,y2,c;
scanf("%d%d%d%d%d",&x1,&x2,&y1,&y2,&c);
return (getsum(x2,y2,c)-getsum(x1-1,y2,c)-getsum(x2,y1-1,c)+getsum(x1-1,y1-1,c));
}
最后,把这些操作拼起来,再加上输入输出与初始化即可。
#include <bits/stdc++.h>
using namespace std;
int n,m,q,a[301][301],c[301][301][101],op;
int lowbit(int x)
{
return (x&(-x));
}
void add(int x,int y,int k,int s)
{
int i=x,j=y;
while(x<=n)
{
y=j;
while(y<=m)c[x][y][s]+=k,y+=lowbit(y);
x+=lowbit(x);
}
}
void insert()
{
int x=0,y=0,c=0;
scanf("%d%d%d",&x,&y,&c);
add(x,y,1,c);
add(x,y,-1,a[x][y]);
a[x][y]=c;
}
int getsum(int x,int y,int k)
{
int t=0,i=x,j=y;
while(x>0)
{
y=j;
while(y>0)t+=c[x][y][k],y-=lowbit(y);
x-=lowbit(x);
}
return t;
}
int query()
{
int x1,y1,x2,y2,c;
scanf("%d%d%d%d%d",&x1,&x2,&y1,&y2,&c);
return (getsum(x2,y2,c)-getsum(x1-1,y2,c)-getsum(x2,y1-1,c)+getsum(x1-1,y1-1,c));
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf("%d",&a[i][j]);
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
add(i,j,1,a[i][j]);
scanf("%d",&q);
for(int i=0;i<q;i++)
{
scanf("%d",&op);
if(op==1)insert();
else if(op==2)printf("%d\n",query());
}
return 0;
}
区间修改+单点查询
树状数组支持单点查询,区间修改(一般是求和)。
单点修改,区间查询使用的是前缀和思想,把它反过来,变成差分思想,就能够实现单点查询,区间修改。
首先建立一个差分数组,其中每个值定义为:
之后,在差分数组上建立树状数组。
单点查询
同单点修改,区间查询的查询前缀和。
因为由差分数组的定义,可以知道差分数组前 \(i\) 项的和为:
所以,可以直接在差分数组上查询前 \(i\) 项的前缀和,就是 \(a_i\) 的值。
int getsum(int x)
{
int t=0;
while(x>0)t+=c[x],x-=lowbit(x);
return t;
}
时间复杂度:\(O(\log n)\)
区间修改
对于 \([l,r]\) 区间增加 \(k\) 的修改,可以把位置分为一下几类:
\(1\) :\(l\lt i\le r\)
没有变化,无需修改。
\(2\) :\(i=l\)
按照之前的修改操作将第 \(l\) 项 \(+k\) 即可。
\(3\) :\(i=r+1\)
按照之前的修改操作将第 \(r+1\) 项 \(-k\) 即可。
void add(int x,int d)
{
while(x<=n)c[x]+=d,x+=lowbit(x);
}
void pluss()
{
int x,y,k;
scanf("%d%d%d",&x,&y,&k);
add(x,k);add(y+1,-k);
}
时间复杂度:\(O(\log n)\)
初始化
在差分数组上建立树状数组。
void init()
{
for(int i=1;i<=n;i++)add(i,b[i]);
}
时间复杂度:\(O(n\log n)\)
区间修改+单点查询例题
例题 \(5\) :
区间修改+单点查询模板题,不多赘述。
#include <bits/stdc++.h>
using namespace std;
int n,m,a[600000],b[600000],c[600000];
int lowbit(int x)
{
return (x&(-x));
}
void add(int x,int k)
{
while(x<=n)c[x]+=k,x+=lowbit(x);
}
void init()
{
for(int i=1;i<=n;i++)add(i,b[i]);
}
int getsum(int x)
{
int ans=0;
while(x>0)ans+=c[x],x-=lowbit(x);
return ans;
}
void pluss()
{
int x,y,k;
scanf("%d%d%d",&x,&y,&k);
add(x,k);add(y+1,-k);
}
int ask()
{
int x;
scanf("%d",&x);
return getsum(x);
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)scanf("%d",&a[i]);
for(int i=1;i<=n;i++)b[i]=a[i]-a[i-1];
init();
for(int i=1;i<=m;i++)
{
int op;
scanf("%d",&op);
if(op==1)pluss();
else if(op==2)printf("%d\n",ask());
}
return 0;
}
例题 \(6\) :
同例题 \(5\) ,不用初始化。
对于数字反转,可以修改时直接将数字加 \(1\) ,查询时利用对 \(2\) 取模的周期性来解决。
#include <bits/stdc++.h>
using namespace std;
int n,m,b[600000],c[600000];
int lowbit(int x)
{
return (x&(-x));
}
void add(int x,int k)
{
while(x<=n)c[x]+=k,x+=lowbit(x);
}
int getsum(int x)
{
int ans=0;
while(x>0)ans+=c[x],x-=lowbit(x);
return ans;
}
void pluss()
{
int x,y,k=1;
scanf("%d%d",&x,&y);
add(x,k);add(y+1,-k);
}
int ask()
{
int x;
scanf("%d",&x);
return (getsum(x)+2)%2;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int op;
scanf("%d",&op);
if(op==1)pluss();
else if(op==2)printf("%d\n",ask());
}
return 0;
}
树状数组求逆序对
一般来说,可以使用归并排序来求一个序列中的逆序对数。但是,树状数组也可以完成。
其中步骤如下:
\(1\) :将数组离散化,映射到 \(1\sim n\) 。
教练推荐的离散化博客:浅谈数据的离散化
\(2\) :建立一个树状数组,\(c_i\) 表示离散化后数字 \(i\) 出现的次数。
\(3\) :从左到右依次遍历数组,设这个 \(a_i\) 为 \(k\) 每次修改对应 \(c_k\) ,进行一次 \(+1\) 。然后根据数组有序时的要求是升序还是降序,查询 \([k+1,n]\) 或 \([1,k-1]\) 的区间和,累加进 \(ans\) 。
\(4\) :结束,输出 \(ans\) 。
树状数组求逆序对用到的是单点修改+区间查询的树状数组。
树状数组求逆序对例题
例题 \(7\) :
求逆序对数板子题,可以归并排序,亦可树状数组,这里使用树状数组,不多赘述。
#include <bits/stdc++.h>
using namespace std;
struct node
{
long long x,y;
}a[600000];
long long n,m,ans=0,b[600000],c[600000];
bool cmp(struct node a,struct node b)
{
return a.y<b.y;
}
long long lowbit(long long x)
{
return (x&(-x));
}
void add(long long x,long long d)
{
while(x<=n)c[x]+=d,x+=lowbit(x);
}
void init()
{
sort(a+1,a+n+1,cmp);
b[a[1].x]=++m;
for(long long i=2;i<=n;i++)
if(a[i].y!=a[i-1].y)b[a[i].x]=++m;
else b[a[i].x]=m;
}
long long getsum(long long x)
{
long long t=0;
while(x>0)t+=c[x],x-=lowbit(x);
return t;
}
int main()
{
scanf("%lld",&n);
for(long long i=1;i<=n;i++)
{
scanf("%lld",&a[i].y);
a[i].x=i;
}
init();
for(long long i=1;i<=n;i++)
{
add(b[i],1);
ans+=(i-getsum(b[i]));
}
printf("%lld",ans);
return 0;
}
例题 \(8\) :
实质就是求一个数组的逆序对数,推导过程可以看 零碎知识点整理 杂项部分 \(3.2\) 的证明部分。
#include <bits/stdc++.h>
using namespace std;
struct node
{
long long x,y;
}a[600000];
long long n,m,ans=0,b[600000],c[600000];
bool cmp(struct node a,struct node b)
{
return a.y<b.y;
}
long long lowbit(long long x)
{
return (x&(-x));
}
void add(long long x,long long d)
{
while(x<=n)c[x]+=d,x+=lowbit(x);
}
void init()
{
sort(a+1,a+n+1,cmp);
b[a[1].x]=++m;
for(long long i=2;i<=n;i++)
if(a[i].y!=a[i-1].y)b[a[i].x]=++m;
else b[a[i].x]=m;
}
long long getsum(long long x)
{
long long t=0;
while(x>0)t+=c[x],x-=lowbit(x);
return t;
}
int main()
{
scanf("%lld",&n);
for(long long i=1;i<=n;i++)
{
scanf("%lld",&a[i].y);
a[i].x=i;
}
init();
for(long long i=1;i<=n;i++)
{
add(b[i],1);
ans+=(i-getsum(b[i]));
}
printf("%lld",ans);
return 0;
}
例题 \(9\) :
首先,为了计算方便,可以以中间那个数,也就是 \(a_j\) 为基准。设在在这个数之前有 \(n\) 个数比它小,在这个数之后有 \(m\) 个数比它大,那么由于前后各自任选一个就能构成一组 thair ,根据乘法原理得到 \(ans\) 应该累加 \(n\times m\) 。
我们可以进行两次树状数组求逆序对:第一次求某个数之前比它小的数的个数,第二次反转序列,求某个数之后比它大的数的个数。
由于 \(a_i\) 的范围很小,所以不用离散化,但是 警示后人(73pts,WA on #4 #9 #10) 。
#include <bits/stdc++.h>
using namespace std;
long long n,ans=0,maxn=0,a[300000],c[300000],ls[300000],rb[300000];
long long lowbit(long long x)
{
return (x&(-x));
}
void add(long long x,long long d)
{
while(x<=maxn)c[x]+=d,x+=lowbit(x);
}
long long getsum(long long x)
{
long long t=0;
while(x>0)t+=c[x],x-=lowbit(x);
return t;
}
int main()
{
scanf("%lld",&n);
for(long long i=1;i<=n;i++)
{
scanf("%lld",&a[i]);
maxn=max(maxn,a[i]);
}
for(long long i=1;i<=n;i++)
{
add(a[i],1);
ls[i]=getsum(a[i]-1);
}
memset(c,0,sizeof(c));
for(long long i=n;i>=1;i--)
{
add(a[i],1);
rb[i]=getsum(maxn)-getsum(a[i]);
}
for(long long i=1;i<=n;i++)
ans+=ls[i]*rb[i];
printf("%lld\n",ans);
return 0;
}
例题 \(10\) :
排序题目的巅峰。
首先,由于距离是两数之差的平方,有一个显然的贪心:把两个数组从小到大排序,同一位置的数互相对应,此时距离最小。交换两数后,由于平方的影响,绝对值之差会较大,导致距离也较大,证明了贪心的正确性。
然后,将 \(a\) 数组的每个数与 \(b\) 数组建立映射关系,同时进行离散化。可以记录下数组 \(a\) 中每个数字排序前的位置,再以排序后其对应的 \(b\) 数组的元素的位置作为关键字进行离散化。这样相当于数组中记录的是在不改变 \(b\) 数组的情况下,每个数组元素在距离最小情况下的排名。
由于数组记录的是排名,那么最小情况必然是一个单升不降的序列。此时的序列是一个乱序序列,要求最小化将这个序列排好序的相邻两数交换次数。这点就很像例题 \(8\) ,实质就是求一个数组的逆序对数,树状数组求解即可,推导过程可以看 零碎知识点整理 杂项部分 \(3.2\) 的证明部分。
由于每次交换,逆序对数量要么 \(+1\) ,要么 \(-1\) ,两个序列地位相同,可以只变换一个序列,最终最优解不受影响,再次保证了算法的正确性。
#include <bits/stdc++.h>
const int MOD=100000000-3;
using namespace std;
struct node
{
int x,v;
}a[200000],b[200000];
long long n,m=1,ans,c[200000],d[200000];
bool cmp(struct node a,struct node b)
{
return a.v<b.v;
}
long long lowbit(long long x)
{
return (x&(-x));
}
void add(long long x,long long k)
{
while(x<=m)c[x]+=k,x+=lowbit(x);
}
long long getsum(long long x)
{
long long ans=0;
while(x>0)ans+=c[x],x-=lowbit(x);
return ans;
}
int main()
{
scanf("%lld",&n);
for(int i=1;i<=n;i++)
{
scanf("%lld",&a[i].v);
a[i].x=i;
}
for(int i=1;i<=n;i++)
{
scanf("%lld",&b[i].v);
b[i].x=i;
}
sort(a+1,a+n+1,cmp);
sort(b+1,b+n+1,cmp);
for(int i=1;i<=n;i++)
{
if(i!=1&&a[i].v!=a[i-1].v)m++;
d[a[i].x]=b[i].x;
}
for(int i=1;i<=n;i++)
{
add(d[i],1);
ans+=((getsum(m)%MOD-getsum(d[i])%MOD)+MOD)%MOD;
ans%=MOD;
}
printf("%lld\n",ans%MOD);
return 0;
}
后记
树状数组讲了两个星期,可见其内容之多,共 \(995\) 行。
数据结构果然毒瘤啊qaq



 浙公网安备 33010602011771号
浙公网安备 33010602011771号