【5】KMP学习笔记
前言
WFLS 2023 寒假集训 Day1
KMP好闪,拜谢KMP!
暴力算法
单模字符串匹配算法
设 \(i\) 为主串 \(s\)(文本串)指针,\(j\) 为子串 \(t\)(模式串)指针,最开始 \(i,j\) 都从 \(0\) 开始,如果 \(s[i]==t[j]\) 那么 \(i++\) , \(j++\) 。否则匹配失败(失配),则 \(i=i-j+1\) , \(j=0\) 。
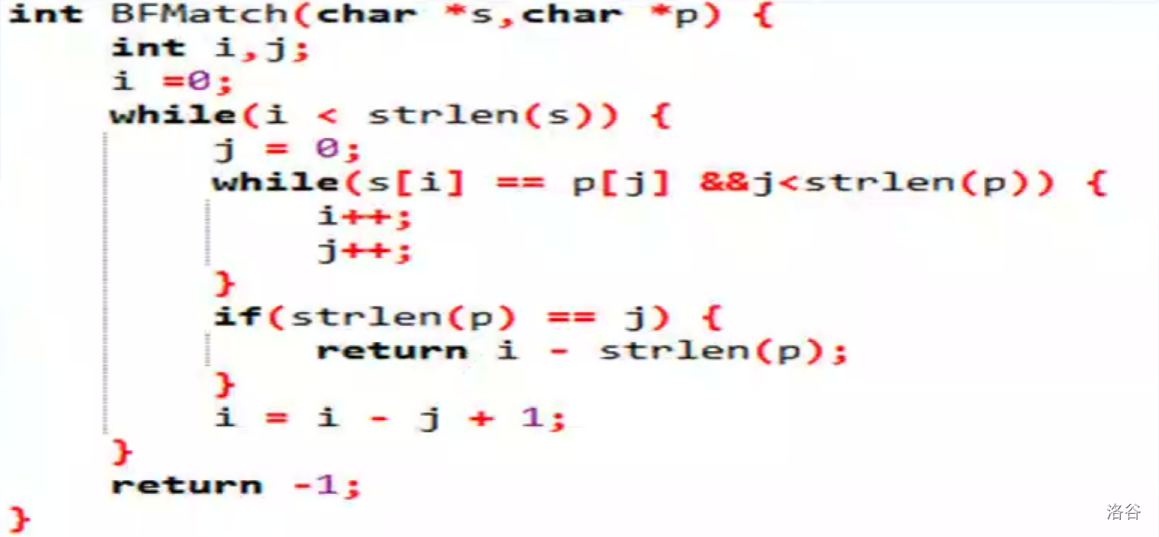
时间复杂度: \(O(mn)\)
KMP
首先我们要思考,暴力算法慢在哪里。
最主要的问题,就是这一句话:
i=i-j+1;
有没有办法可以使主指针 \(i\) 不回溯呢?
next数组
如果匹配到 \(t[j]\) 时失配,那么前 \(j-1\) 项肯定匹配。
这时就要考虑使用模式串自身的性质了。
举个例子:
asbhguwsdwqqddwsdwsdwsr
wsdwsr
^ ^
i j
此时在 \(j\) 处失配了,但是根据观察,我们可以把模式串挪到下面位置,从而减少运算量。
asbhguwsdwqqddwsdwsdwsr
wsdwsr
^
i,j
由于在模式串中的前 \(j-1\) 项已经匹配了,所以我们可以在前 \(j-1\) 项中找到一个前缀,使其与后面第 \(j\) 项之前的某一段相同,然后就可以直接跳到这一段,继续进行匹配。
这是就要引入一个概念了:最大公共前缀
其实就是上面说的 一个前缀 ,在进行KMP算法时,可以把每个 \(j\) 的最大公共前缀存进一个表中,这个表就是next数组。
例如字符串 wsdwsr 的next数组
| w | s | d | w | s | r | |
|---|---|---|---|---|---|---|
| \(next[j]\) | \(-1\) | \(0\) | \(0\) | \(0\) | \(1\) | \(2\) |
求next数组的方法:
设现在算到了第 \(n\) 位
\(1\) :第一位的next值为 \(-1\)
\(2\) :查看第 \(n-1\) 位的next值,记为 \(a\)
\(3\) :判断 \(a\) 是否为 \(-1\) ,如果 \(a\) 为 \(-1\) ,则 \(next[n]=0\)
\(4\) :否则将第 \(n-1\) 个字符与第 \(a\) 个字符进行比较
\(5\) :若相同,则 \(next[n]=a+1\)
\(6\) :若不相同,则令 \(a=next[a]\) ,执行第 \(3\) 步。
计算完毕后,\(next[n]\) 就表示前 \(n-1\) 个字符的最大公共前缀。
模板如下:
int getnext(char t[],int next[])
{
int i=0,j=-1,res=-2;
next[0]=-1;
int l=strlen(t);
while(i<l)
{
if(j==-1||t[i]==t[j])
{
i++;
j++;
next[i]=j;
}
else j=next[j];
}
for(int i=0;i<l;i++)
res=max(res,next[i]);
return res;
}
单模字符串匹配
有了 \(next\) 表,在匹配过程中如果失配,我们可以直接令 \(j=next[j]\) ,查表跳转到最大公共前缀的后一个位置就行了。
模板如下:
int kmp(char s[],char t[],int next[])
{
int i=0,j=0,cnt=0;
int ls=strlen(s),lt=strlen(t);
while(i<ls)
{
if(j==-1||s[i]==t[j])
{
i++;
j++;
}
else j=next[j];
if(j==lt)
{
printf("%d\n",i-lt+1);
j=next[j];
cnt++;
}
}
return cnt;
}
复杂度分析
时间复杂度: \(O(m+n)\) (听说可以被卡回 \(O(mn)\) )
空间复杂度: \(O(m)\)
KMP例题
例题 \(1\) :
KMP板子题,注意匹配成功时的处理,不多赘述。
#include <bits/stdc++.h>
using namespace std;
char s[1000010],t[1000010];
int next1[1000010];
int getnext(char t[],int next[])
{
int i=0,j=-1,res=-2;
next[0]=-1;
int l=strlen(t);
while(i<l)
{
if(j==-1||t[i]==t[j])
{
i++;
j++;
next[i]=j;
}
else j=next[j];
}
for(int i=0;i<l;i++)
res=max(res,next[i]);
return res;
}
int kmp(char s[],char t[],int next[])
{
int i=0,j=0,cnt=0;
int ls=strlen(s),lt=strlen(t);
while(i<ls)
{
if(j==-1||s[i]==t[j])
{
i++;
j++;
}
else j=next[j];
if(j==lt)
{
printf("%d\n",i-lt+1);
j=next[j];
cnt++;
}
}
return cnt;
}
int main()
{
scanf("%s",s);
scanf("%s",t);
int ans=getnext(t,next1);
int cnt=kmp(s,t,next1);
int l=strlen(t);
for(int i=1;i<=l;i++)
printf("%d ",next1[i]);
return 0;
}
例题 \(2\) :
P4391 [BOI2009]Radio Transmission 无线传输
此题最大的难点在于如何求出一个周期。
我们可以求出整个字串的最大公共前缀,然后开始分类讨论:
\(1\) :周期是完整的
最大公共前缀大致是这样:
周期 周期 ... 周期 周期
—————————————————— (前缀)
——————————————————— (与前缀相同的部分)
此时,用字符串总长度减去最大公共前缀的长度就是答案,也就是 \(n-next[n]\) 。
\(2\) :周期不是完整的
最大公共前缀大致是这样:
半周 周期 ... 周期 半周
—————————————————— (前缀)
——————————————————— (与前缀相同的部分)
把中间的一堆完整周期看作一个周期,因为无论有多少个整周期都没有影响,问题就变成了这样:
半周 周期 半周
———————— (前缀)
———————— (与前缀相同的部分)
由最大公共前缀,得到这两段是完全相同的。所以可以把前面的半周对应到底下的前周,就是这样:
半周 前周 后周 半周
————————————— (前缀)
————————————(与前缀相同的部分)
西周 东周 周天子
所以前面的半周与前周完全相同,就可以把前面的半周都消掉,同理也可以消掉后周,就变成了:
半周 周期 ... 周期 半周
—————————————————— (前缀)
——————————————————— (与前缀相同的部分)
结论还是 \(n-next[n]\) 。
#include <bits/stdc++.h>
using namespace std;
char t[1000010];
int next1[1000010];
int getnext(char t[],int next[])
{
int i=0,j=-1,res=-2;
next[0]=-1;
int l=strlen(t);
while(i<l)
{
if(j==-1||t[i]==t[j])
{
i++;
j++;
next[i]=j;
}
else j=next[j];
}
for(int i=0;i<l;i++)
res=max(res,next[i]);
return res;
}
int main()
{
int ans;
scanf("%d%s",&ans,t);
getnext(t,next1);
printf("%d",ans-next1[ans]);
return 0;
}
例题 \(3\) :
借用 KMP 思想优化的动态规划。
首先,用 \(dp[i]\) 表示把前 \(i\) 位的字符完全匹配需要的最少词缀数(下标均从 \(1\) 开始)。那么,我们可以从点 \(i+1\) 开始,向后逐位与字符串 \(T\) 比较。设此时匹配到了 \(T\) 中的第 \(j\) 位,如果相等,则易得转移方程:
如果不相等或到达了字符串 \(T\) 末尾,则证明在此之后不会更长的有魔法词缀,可以结束这一次匹配,令 \(i=i+1\) 计算下一位即可。
很明显,这个算法的时间复杂度是 \(O(|S||T|)\) 的,当数据范围达到 \(|S|,|T|\le10^6\) 时,算法必然超时。
考虑优化这个算法,我们知道,如果不相等或到达了字符串 \(T\) 末尾,失配后是可以直接跳过一部分不可能产生新的解的数据。这样就自然而然地想到了用这个思想把单模字符串匹配优化到 \(O(|S|+|T|)\) 的 KMP 算法。
借助 KMP 的思想,首先求出字符串 \(T\) 的 \(next\) 数组,然后开始按照 KMP 的方式匹配:(设此时文本串匹配到第 \(i\) 项,模式串匹配到第 \(j\) 项)
设置一个名为 \(now\) 的临时变量,用于存储如果匹配的最少词缀数。
可以直接逐位比较。如果相等,则按照 KMP 思想,将模式串和文本串指针一起后移,令 \(dp[i]=now\) 后比较下一位。
如果不相等,可以令 \(j=next[j]\) 之后重新计算 \(now\) 的值。因为一旦匹配失败,只能再次选择一个词缀。每次 KMP 算法在匹配失败后,会利用最长公共前后缀的性质使得文本串指针 \(i\) 不往前跳。而每次利用最长公共前后缀的性质,会改变模式串匹配的起始位置,所以需要重新计算 \(now\) 的值。可以直接用 \(dp[i-j]\) 计算出模式串匹配的起始位置的前一个位置,把 \(now\) 的值更新为 \(dp[i-j]+1\) 以保证正确性。模式串匹配到末尾也是同理。
DP 边界:\(dp[0]=1\)。
DP 目标:\(dp[|S|]\)。
时间复杂度:\(O(|S|+|T|)\)。
注意,由于有无解的情况,所以当 \(next\) 数组跳到 \(-1\) 时,应该直接判定无解并输出 Fake。因为如果 \(next\) 数组跳到 \(-1\) 证明匹配第一个字符就失配了,此时后面没有办法再进行匹配,无解。
完整代码:(由于代码中的字符串下标是从 \(0\) 开始的,所以可能会和上文的讲解有些出入)
#include <bits/stdc++.h>
using namespace std;
int lt,ls,next1[10000010],f[10000010];
char t[10000010],s[10000010];
void get_next(char t[],int next[])
{
int i=0,j=-1;
next[0]=-1;
while(i<lt)
{
if(j==-1||t[i]==t[j])i++,j++,next[i]=j;
else j=next[j];
}
}
bool kmp(char s[],char t[],int next[])
{
int i=0,j=0,now=1;
f[0]=1;
while(i<ls)
{
if(j==-1)return 0;
if(s[i]==t[j])i++,j++,f[i]=now;
else j=next[j],now=f[i-j]+1;
if(j==lt)now=f[i-j]+1,j=next[j];
}
return 1;
}
int main()
{
scanf("%d%d%s%s",<,&ls,t,s);
get_next(t,next1);
if(!kmp(s,t,next1))printf("Fake");
else printf("%d",f[ls]);
return 0;
}
后记
为什么只有两道例题?因为别的我不会
UPD on 2024/6/23 现在有三道例题了。
集训真的好累好累啊,眼睛受不了的!
不过能提升我的OI水平,想想也没什么的。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号