数据结构丨二叉树
树的遍历
树的遍历-介绍
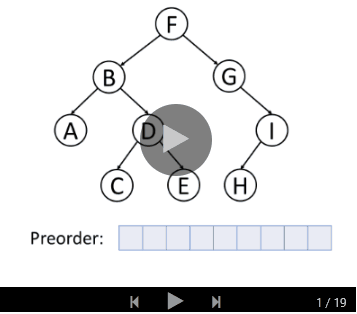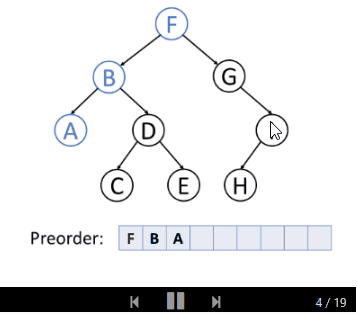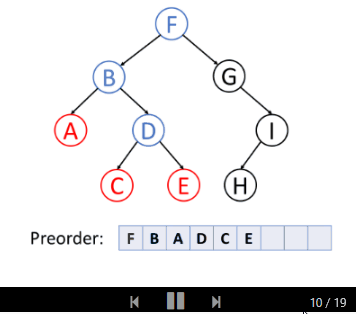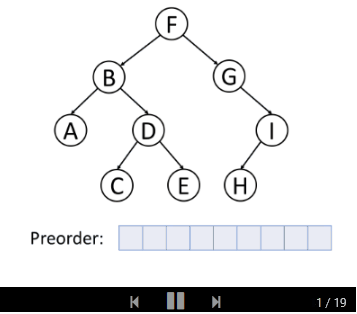
前序遍历
前序遍历首先访问根节点,然后遍历左子树,最后遍历右子树。
请看下面的例子:
中序遍历
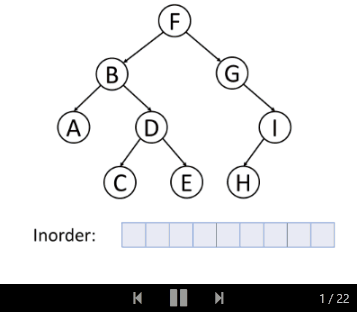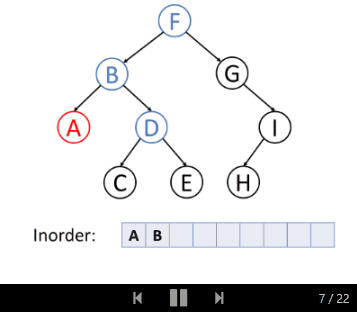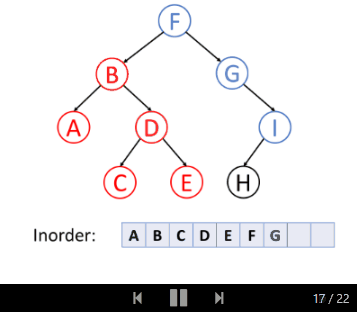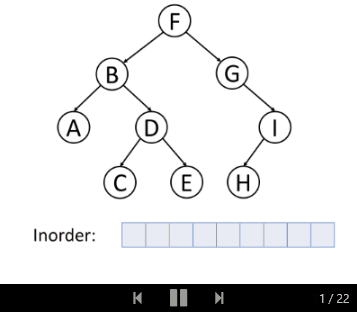
中序遍历是先遍历左子树,然后访问根节点,然后遍历右子树。
让我们一起来看树的中序遍历:
后序遍历
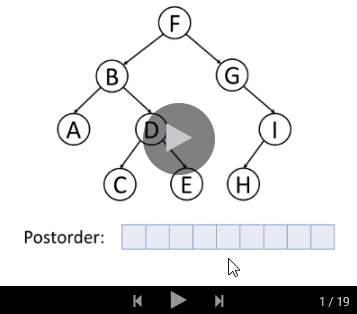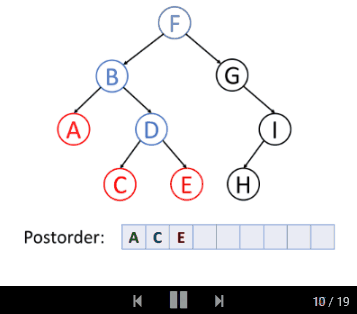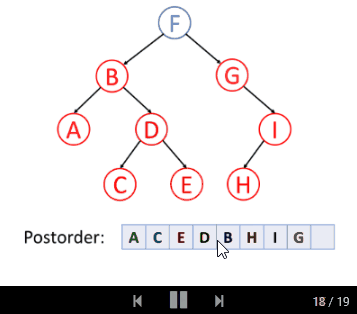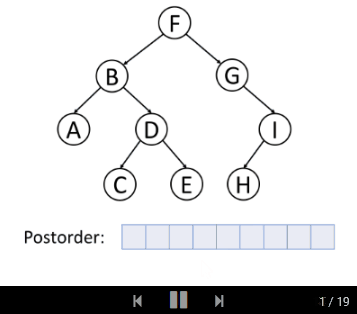
后序遍历是先遍历左子树,然后遍历右子树,最后访问树的根节点。
我们一起来看后序遍历的动画演示:
值得注意的是,当你删除树中的节点时,删除过程将按照后序遍历的顺序进行。 也就是说,当你删除一个节点时,你将首先删除它的左节点和它的右边的节点,然后再删除节点本身。
另外,后序在数学表达中被广泛使用。 编写程序来解析后缀表示法更为容易。 这里是一个例子:
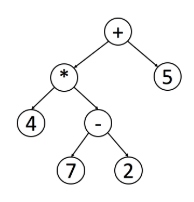
您可以使用中序遍历轻松找出原始表达式。 但是程序处理这个表达式时并不容易,因为你必须检查操作的优先级。
如果你想对这棵树进行后序遍历,使用栈来处理表达式会变得更加容易。 每遇到一个操作符,就可以从栈中弹出栈顶的两个元素,计算并将结果返回到栈中。
递归和迭代
请练习文章后面习题中的三种遍历方法。 您可以通过递归或迭代方法实现算法,并比较它们之间的差异。
二叉树的前序遍历
给定一个二叉树,返回它的 前序 遍历。
示例:
输入: [1,null,2,3]
1
\
2
/
3
输出: [1,2,3]
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
struct TreeNode{
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x):val(x),left(NULL),right(NULL){}
};
// Recursive
// Time Complexity: O(n), n is the node number in the tree
// Space Complexity: O(h), h is the height of the tree
class SolutionA{
public:
vector<int> preorderTraversal(TreeNode* root){
vector<int> res;
preorderTraversal(root, res);
return res;
}
private:
void preorderTraversal(TreeNode* node, vector<int> &res){
if(node){
res.push_back(node->val);
preorderTraversal(node->left, res);
preorderTraversal(node->right, res);
}
}
};
// Classic Non-Recursive algorithm for preorder traversal
// Time Complexity: O(n), n is the node number in the tree
// Space Complexity: O(h), h is the height of the tree
class SolutionB{
public:
vector<int> preorderTraversal(TreeNode* root){
vector<int> res;
if(root == NULL);
return res;
stack<TreeNode*> stack;
stack.push(root);
while(!stack.empty()){
TreeNode* curNode = stack.top();
stack.pop();
res.push_back(curNode->val);
if(curNode->right)
stack.push(curNode->right);
if(curNode->left)
stack.push(curNode->left);
}
return res;
}
}
int main(){
return 0;
}
二叉树的中序遍历
给定一个二叉树,返回它的中序 遍历。
示例:
输入: [1,null,2,3]
1
\
2
/
3
输出: [1,3,2]
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
/// Definition for a binary tree node.
struct TreeNode{
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x):val(x), left(NULL), right(NULL){}
};
// Recursive
// Time Complexity: O(n), n is the node number in the tree
// Space Complexity: O(h), h is the height of the tree
class SolutionA{
public:
vector<int> inorderTraversal(TreeNode* root){
vector<int> res;
__inorderTraversal(root, res);
return res;
}
private:
void __inorderTraversal(TreeNode* node, vector<int>& res){
if(node){
__inorderTraversal(node->left, res);
res.push_back(node->val);
__inorderTraversal(node->right, res);
}
}
};
// Classic Non-Recursive algorithm for inorder traversal
// Time Complexity: O(n), n is the node number in the tree
// Space Complexity: O(h), h is the height of the tree
class SolutionB{
public:
vector<int> inorderTraversal(TreeNode* root){
vector<int> res;
if(root == NULL)
return res;
stack<TreeNode*> stack;
TreeNode* cur = root;
while(cur != NULL || !stack.empty()){
//先到达左下端
while(cur != NULL){
stack.push(cur);
cur = cur->left;
}
cur = stack.top();
stack.pop();
res.push_back(cur->val);
cur = cur->right;
}
return res;
}
};
二叉树的后序遍历
给定一个二叉树,返回它的 后序 遍历。
示例:
输入: [1,null,2,3]
1
\
2
/
3
输出: [3,2,1]
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
struct TreeNode{
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x): val(x), left(NULL), right(NULL){}
};
// Recursive
// Time Complexity: O(n), n is the node number in the tree
// Space Complexity: O(h), h is the height of the tree
class SolutionA{
public:
vector<int> postorderTraversal(TreeNode* root){
vector<int> res;
__postorderTraversal(root, res);
return res;
}
private:
void __postorderTraversal(TreeNode* node, vector<int> &res){
if(node){
__postorderTraversal(node->left, res);
__postorderTraversal(node->right, res);
res.push_back(node->val);
}
}
};
// Classic Non-Recursive
// Using a pre pointer to record the last visted node
//
// Time Complexity: O(n)
// Space Complexity: O(h)
class SolutionB{
public:
vector<int> postorderTraversal(TreeNode* root){
vector<int> res;
if(root == NULL)
return res;
stack<TreeNode*> stack;
TreeNode* pre = NULL;
TreeNode* cur = root;
while(cur != NULL || !stack.empty()){
//到达最左下端
while(cur != NULL){
stack.push(cur);
cur = cur->left;
}
cur = stack.top();
stack.pop();
//确保该节点没有右子树或者右子树已遍历过
if(cur->right == NULL || pre == cur->right){
res.push_back(cur->val);
pre = cur;
cur = NULL;
}
else{
stack.push(cur);
cur = cur->right;
}
}
return res;
}
};
层次遍历-介绍
层序遍历就是逐层遍历树结构。
广度优先搜索是一种广泛运用在树或图这类数据结构中,遍历或搜索的算法。 该算法从一个根节点开始,首先访问节点本身。 然后遍历它的相邻节点,其次遍历它的二级邻节点、三级邻节点,以此类推。
当我们在树中进行广度优先搜索时,我们访问的节点的顺序是按照层序遍历顺序的。
这是一个层序顺序遍历的例子:
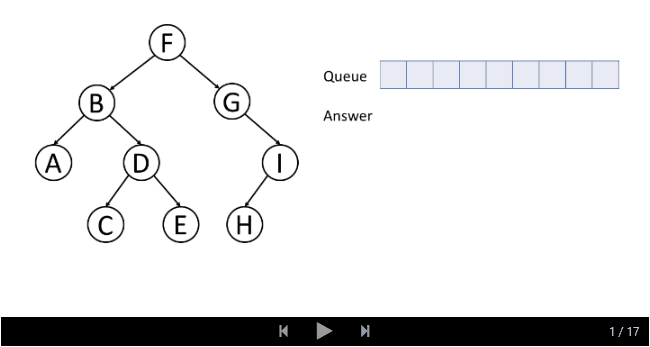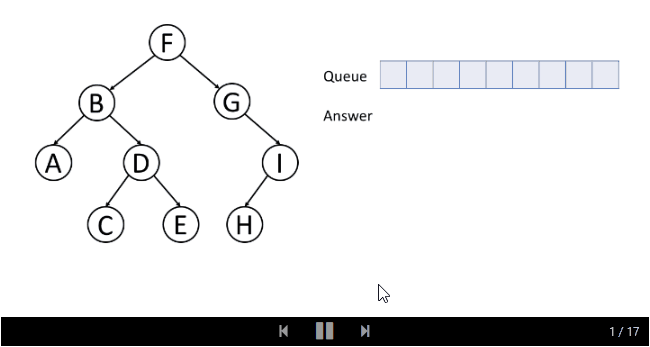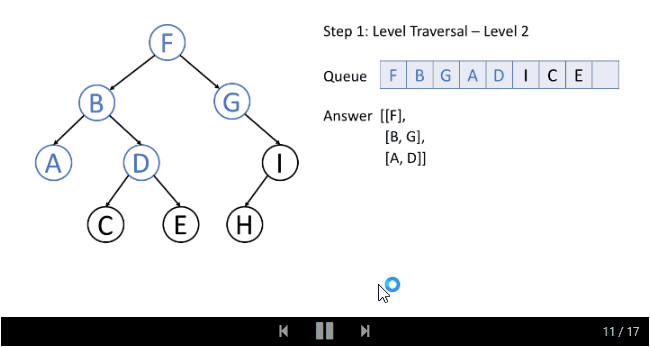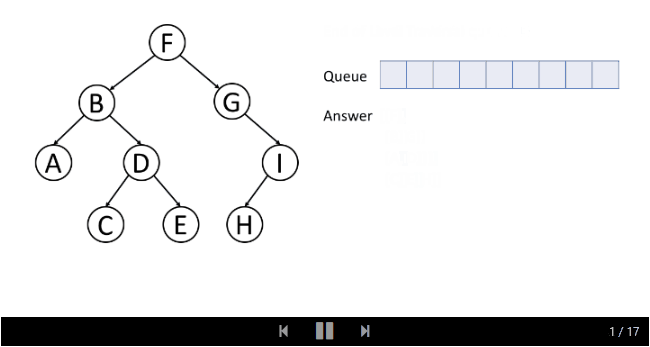
通常,我们使用一个叫做队列的数据结构来帮助我们做广度优先搜索。 如果您对队列不熟悉,可以在我们即将推出的另一张卡片中找到更多有关信息。
二叉树的层次遍历
给定一个二叉树,返回其按层次遍历的节点值。 (即逐层地,从左到右访问所有节点)。
例如:
给定二叉树: [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回其层次遍历结果:
[
[3],
[9,20],
[15,7]
]
#include <iostream>
#include <vector>
#include <queue>
#include <cassert>
using namespace std;
struct TreeNode{
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x): val(x), left(NULL), right(NULL){}
};
/// BFS
/// Time Complexity: O(n), where n is the number of nodes in the tree
/// Space Complexity: O(n)
class Solution{
public:
vector<vector<int>> levelOrder(TreeNode* root){
vector<vector<int>> res;
if(root == NULL)
return res;
queue<pair<TreeNode*, int>> q;
q.push(make_pair(root, 0));
while(!q.empty()){
TreeNode* node = q.front().first;
int level = q.front().second;
q.pop();
if(level == res.size())
res.push_back(vector<int>());
assert(level <res.size());
res[level].push_back(node->val);
if(node->left)
q.push(make_pair(node->left, level+1));
if(node->right)
q.push(make_pair(node->right, level+1));
}
return res;
}
};
运用递归解决问题
运用递归解决树的问题
在前面的章节中,我们已经介绍了如何利用递归求解树的遍历。 递归是解决树的相关问题最有效和最常用的方法之一。
我们知道,树可以以递归的方式定义为一个节点(根节点),它包括一个值和一个指向其他节点指针的列表。 递归是树的特性之一。 因此,许多树问题可以通过递归的方式来解决。 对于每个递归层级,我们只能关注单个节点内的问题,并通过递归调用函数来解决其子节点问题。
通常,我们可以通过 “自顶向下” 或 “自底向上” 的递归来解决树问题。
“自顶向下” 的解决方案
“自顶向下” 意味着在每个递归层级,我们将首先访问节点来计算一些值,并在递归调用函数时将这些值传递到子节点。 所以 “自顶向下” 的解决方案可以被认为是一种前序遍历。 具体来说,递归函数 top_down(root, params) 的原理是这样的:
1. return specific value for null node
2. update the answer if needed // anwer <-- params
3. left_ans = top_down(root.left, left_params) // left_params <-- root.val, params
4. right_ans = top_down(root.right, right_params) // right_params <-- root.val, params
5. return the answer if needed
例如,思考这样一个问题:给定一个二叉树,请寻找它的最大深度。
我们知道根节点的深度是1。 对于每个节点,如果我们知道某节点的深度,那我们将知道它子节点的深度。 因此,在调用递归函数的时候,将节点的深度传递为一个参数,那么所有的节点都知道它们自身的深度。 而对于叶节点,我们可以通过更新深度从而获取最终答案。 这里是递归函数 maximum_depth(root, depth) 的伪代码:
1. return if root is null
2. if root is a leaf node:
3. answer = max(answer, depth) // update the answer if needed
4. maximum_depth(root.left, depth + 1) // call the function recursively for left child
5. maximum_depth(root.right, depth + 1) // call the function recursively for right child
以下的例子可以帮助你理解它是如何工作的:
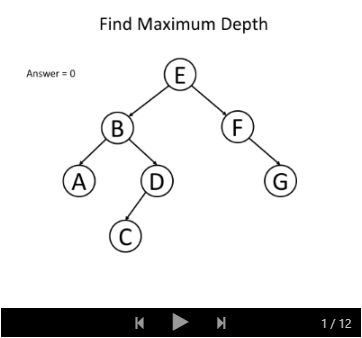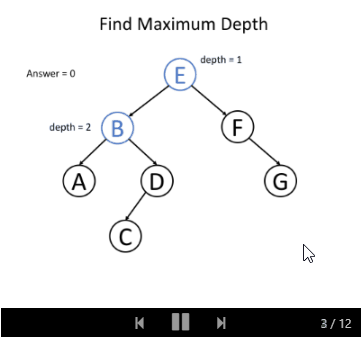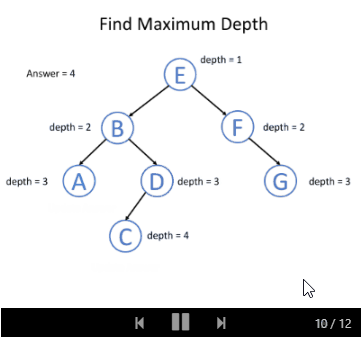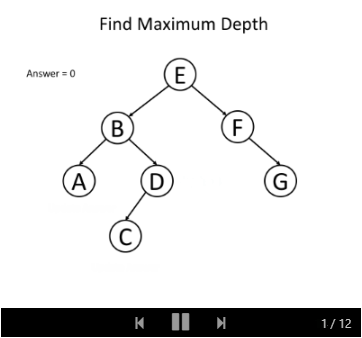
“自底向上” 的解决方案
“自底向上” 是另一种递归方法。 在每个递归层次上,我们首先对所有子节点递归地调用函数,然后根据返回值和根节点本身的值得到答案。 这个过程可以看作是后序遍历的一种。 通常, “自底向上” 的递归函数 bottom_up(root) 为如下所示:
1. return specific value for null node
2. left_ans = bottom_up(root.left) // call function recursively for left child
3. right_ans = bottom_up(root.right) // call function recursively for right child
4. return answers // answer <-- left_ans, right_ans, root.val
让我们继续讨论前面关于树的最大深度的问题,但是使用不同的思维方式:对于树的单个节点,以节点自身为根的子树的最大深度x是多少?
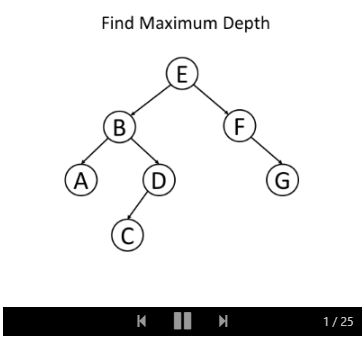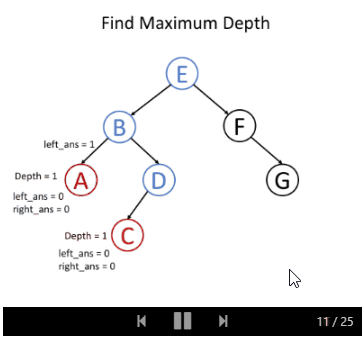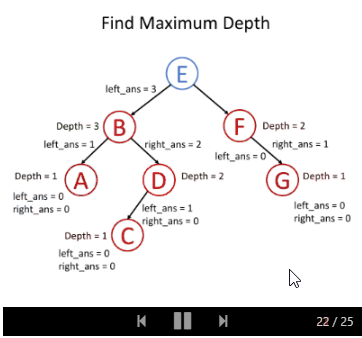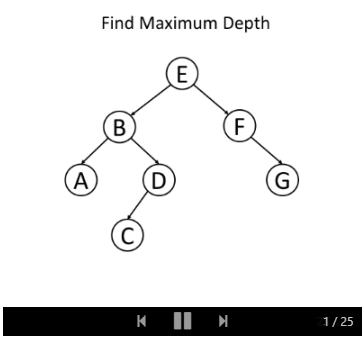
如果我们知道一个根节点,以其左子节点为根的最大深度为l和以其右子节点为根的最大深度为r,我们是否可以回答前面的问题? 当然可以,我们可以选择它们之间的最大值,再加上1来获得根节点所在的子树的最大深度。 那就是 x = max(l,r)+ 1。
这意味着对于每一个节点来说,我们都可以在解决它子节点的问题之后得到答案。 因此,我们可以使用“自底向上“的方法。下面是递归函数 maximum_depth(root) 的伪代码:
1. return 0 if root is null // return 0 for null node
2. left_depth = maximum_depth(root.left)
3. right_depth = maximum_depth(root.right)
4. return max(left_depth, right_depth) + 1 // return depth of the subtree rooted at root
以下的例子可以帮助你理解它是如何工作的:
总结
了解递归并利用递归解决问题并不容易。
当遇到树问题时,请先思考一下两个问题:
- 你能确定一些参数,从该节点自身解决出发寻找答案吗?
- 你可以使用这些参数和节点本身的值来决定什么应该是传递给它子节点的参数吗?
如果答案都是肯定的,那么请尝试使用 “自顶向下” 的递归来解决此问题。
或者你可以这样思考:对于树中的任意一个节点,如果你知道它子节点的答案,你能计算出该节点的答案吗? 如果答案是肯定的,那么 “自底向上” 的递归可能是一个不错的解决方法。
在接下来的章节中,我们将提供几个经典例题,以帮助你更好地理解树的结构和递归。
二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。
#include <iostream>
using namespace std;
struct TreeNode{
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x): val(x), left(NULL), right(NULL){}
};
/// Recursive
/// Time Complexity: O(n), where n is the nodes' number in the tree
/// Space Complexity: O(h), where h is the height of the tree
class Solution{
public:
int maxDepth(TreeNode* root){
if(root == NULL)
return 0;
return 1+max(maxDepth(root->left), maxDepth(root->right));
}
};
int main(){
return 0;
}
对称二叉树
给定一个二叉树,检查它是否是镜像对称的。
例如,二叉树 [1,2,2,3,4,4,3] 是对称的。
1
/ \
2 2
/ \ / \
3 4 4 3
但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:
1
/ \
2 2
\ \
3 3
说明:
如果你可以运用递归和迭代两种方法解决这个问题,会很加分。
#include <iostream>
#include <queue>
using namespace std;
/// Definition for a binary tree node.
struct TreeNode
{
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
/// Recursive
/// No need to revert one child tree
/// See if the two child trees of the root are mirror directly
///
/// Time Complexity: O(n)
/// Space Complexity: O(h)
class SolutionA
{
public:
bool isSymmetric(TreeNode *root)
{
if (root == NULL)
return true;
return is_mirror(root, root);
}
private:
bool is_mirror(TreeNode *root1, TreeNode *root2)
{
if (root1 == NULL && root2 == NULL)
return true;
if (root1 == NULL || root2 == NULL)
return false;
if (root1->val != root2->val)
return false;
return is_mirror(root1->left, root2->right) &&
is_mirror(root1->right, root2->left);
}
};
/// Non-Recursive
/// Using one queues to level traverse the root in different directions
///
/// Time Complexity: O(n)
/// Space Complexity: O(n)
class SolutionB{
public:
bool isSymmetric(TreeNode* root){
if(root == NULL)
return true;
queue<TreeNode*> q;
q.push(root);
q.push(root);
while(!q.empty()){
TreeNode* node1 = q.front();
q.pop();
TreeNode* node2 = q.front();
q.pop();
if(node1 == NULL && node2 == NULL)
continue;
if(node1 == NULL || node2 == NULL)
return false;
if(node1->val != node2->val)
return false;
q.push(node1->left);
q.push(node2->right);
q.push(node1->right);
q.push(node2->left);
}
return true;
}
};
路径总和
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ \
7 2 1
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
#include <iostream>
using namespace std;
/// Definition for a binary tree node.
struct TreeNode
{
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
/// Recursive
/// Time Complexity: O(n), where n is the nodes' number of the tree
/// Space Complexity: O(h), where h is the height of the tree
class Solution
{
public:
bool hasPathSum(TreeNode *root, int sum)
{
if (root == NULL)
return false;
if (root->left == NULL && root->right == NULL)
return sum == root->val;
return hasPathSum(root->left, sum - root->val) || hasPathSum(root->right, sum - root->val);
}
};
int main(){
return 0;
}
总结
从中序与后序遍历序列构造二叉树
根据一棵树的中序遍历与后序遍历构造二叉树。
注意:
你可以假设树中没有重复的元素。
例如,给出
中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]
返回如下的二叉树:
3
/ \
9 20
/ \
15 7
#include <iostream>
#include <vector>
#include <cassert>
#include <algorithm>
using namespace std;
/// Definition for a binary tree node.
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
/// Recursive
/// Time Complexity: O(n*h) where n is the num of node in th tree
/// and h is the height of the tree
/// Space Complexity: O(h)
class Solution {
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
return buildTree(inorder, 0, inorder.size(), postorder, 0, postorder.size());
}
private:
TreeNode* buildTree(vector<int>& inorder, int inorderL, int inorderR,
vector<int>& postorder, int postorderL, int postorderR){
if(inorderL >= inorderR){
assert(postorderL >= postorderR);
return NULL;
}
if(inorderL + 1 == inorderR){
assert(postorderL + 1 == postorderR);
return new TreeNode(inorder[inorderL]);
}
TreeNode* root = new TreeNode(postorder[postorderR - 1]);
int rootPos = find(inorder.begin() + inorderL, inorder.begin() + inorderR, root->val) - inorder.begin();
assert(inorderL <= rootPos && rootPos < inorderR);
int lsize = rootPos - inorderL;
int rsize = inorderR - (rootPos + 1);
root->left = buildTree(inorder, inorderL, inorderL + lsize, postorder, postorderL, postorderL + lsize);
root->right = buildTree(inorder, rootPos + 1, inorderR, postorder, postorderL + lsize, postorderR - 1);
return root;
}
};
int main() {
vector<int> inorder = {9,3,15,20,7};
vector<int> postorder = {9,15,7,20,3};
TreeNode* root = Solution().buildTree(inorder, postorder);
printf("ok");
return 0;
}
从前序与中序遍历序列构造二叉树
根据一棵树的前序遍历与中序遍历构造二叉树。
注意:
你可以假设树中没有重复的元素。
例如,给出
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树:
3
/ \
9 20
/ \
15 7
#include <iostream>
#include <vector>
#include <cassert>
#include <algorithm>
using namespace std;
/// Definition for a binary tree node.
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
/// Recursive
/// Time Complexity: O(n*h) where n is the num of node in th tree
/// and h is the height of the tree
/// Space Complexity: O(h)
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
return buildTree(preorder, 0, preorder.size(), inorder, 0, inorder.size());
}
private:
TreeNode* buildTree(const vector<int>& preorder, int preorderL, int preorderR,
const vector<int>& inorder, int inorderL, int inorderR){
if(inorderL >= inorderR){
assert(preorderL >= preorderR);
return NULL;
}
if(inorderL + 1 == inorderR){
assert(preorderL + 1 == preorderR);
return new TreeNode(inorder[inorderL]);
}
TreeNode* root = new TreeNode(preorder[preorderL]); //就变化了这一行
int rootPos = find(inorder.begin() + inorderL, inorder.begin() + inorderR, root->val) - inorder.begin();
assert(rootPos >= inorderL && rootPos < inorderR);
int lsize = rootPos - inorderL;
int rsize = inorderR - (rootPos + 1);
root->left = buildTree(preorder, preorderL + 1, preorderL + 1 + lsize, inorder, inorderL, rootPos);
root->right = buildTree(preorder, preorderL + 1 + lsize, preorderR, inorder, rootPos + 1, inorderR);
return root;
}
};
int main() {
vector<int> preorder = {3, 9, 20, 15, 7};
vector<int> inorder = {9,3,15,20,7};
TreeNode* root = Solution().buildTree(preorder, inorder);
printf("ok");
return 0;
}
填充每个节点的下一个右侧节点指针
给定一个完美二叉树,其所有叶子节点都在同一层,每个父节点都有两个子节点。二叉树定义如下:
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
示例:
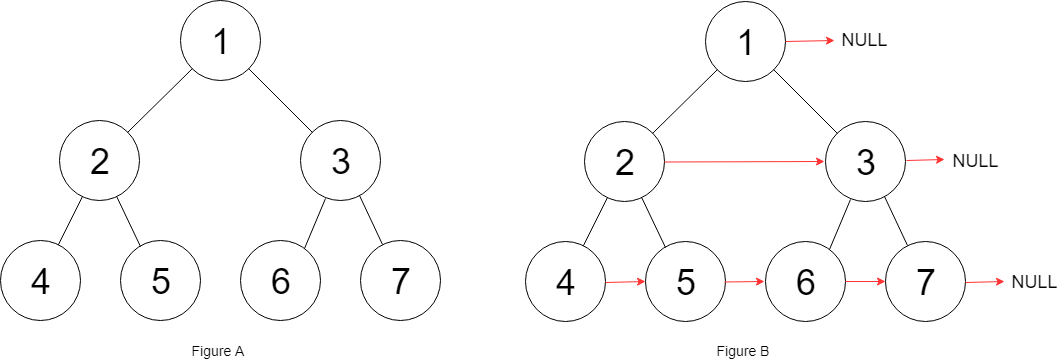
输入:{"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":null,"right":null,"val":4},"next":null,"right":{"$id":"4","left":null,"next":null,"right":null,"val":5},"val":2},"next":null,"right":{"$id":"5","left":{"$id":"6","left":null,"next":null,"right":null,"val":6},"next":null,"right":{"$id":"7","left":null,"next":null,"right":null,"val":7},"val":3},"val":1}
输出:{"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":{"$id":"4","left":null,"next":{"$id":"5","left":null,"next":{"$id":"6","left":null,"next":null,"right":null,"val":7},"right":null,"val":6},"right":null,"val":5},"right":null,"val":4},"next":{"$id":"7","left":{"$ref":"5"},"next":null,"right":{"$ref":"6"},"val":3},"right":{"$ref":"4"},"val":2},"next":null,"right":{"$ref":"7"},"val":1}
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。
提示:
- 你只能使用常量级额外空间。
- 使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
#include <iostream>
#include <queue>
#include <cassert>
using namespace std;
/// Using queue for BFS
/// Time Complexity: O(n)
/// Space Compelxity: O(n)
/// Definition for binary tree with next pointer.
struct TreeLinkNode{
int val;
TreeLinkNode *left, *right, *next;
TreeLinkNode(int x): val(x), left(NULL), right(NULL), next(NULL){}
};
//层次遍历中前一个节点的next指向后一个节点
class SolutionA{
public:
void connect(TreeLinkNode* root){
if(!root) return;
queue<TreeLinkNode*> q;
q.push(root);
int level = 0;
while(!q.empty()){
//移动几位就是二的几次方,跟每层的节点数目相对应
int n = (1 << level);
while(n --){ //遍历每一个节点
TreeLinkNode* cur = q.front();
q.pop();
if(n) //每层的最后一个节点不作处理
cur->next = q.front();
if(cur->left){
q.push(cur->left);
assert(cur->right);
q.push(cur->right);
}
}
level ++;
}
}
};
/// DFS
/// Time Complexity: O(n)
/// Space Compelxity: O(logn)
/// Definition for binary tree with next pointer.
class SolutionB{
public:
void connect(TreeLinkNode* root){
if(!root || !root->left) return;
dfs(root->left, root->right); //所有左节点的next指向右节点
connect(root->left);
connect(root->right);
}
private:
void dfs(TreeLinkNode* l, TreeLinkNode* r){
if(l){
l->next = r;
dfs(l->right, r->left); //所有右节点的next指向左节点
}
}
};
/// BFS without queue
/// Since the upper level have already been a linked list
/// We can traverse the upper level in a linked list way to connect the lower level
/// Actually, the upper linked list is our queue :-)
///
/// Time Complexity: O(n)
/// Space Compelxity: O(1)
/// Definition for binary tree with next pointer.
class SolutionC{
public:
void connect(TreeLinkNode* root){
if(!root) return;
while(root->left){
TreeLinkNode* p = root;
TreeLinkNode* dummyHead = new TreeLinkNode(-1);
TreeLinkNode* cur = dummyHead;
while(p){
cur->next = p->next;
cur = cur->next;
cur->next = p->right;
cur = cur->next;
p = p->next;
}
}
}
}
填充每个节点的下一个右侧节点指针 II
给定一个二叉树
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。
初始状态下,所有 next 指针都被设置为 NULL。
示例:
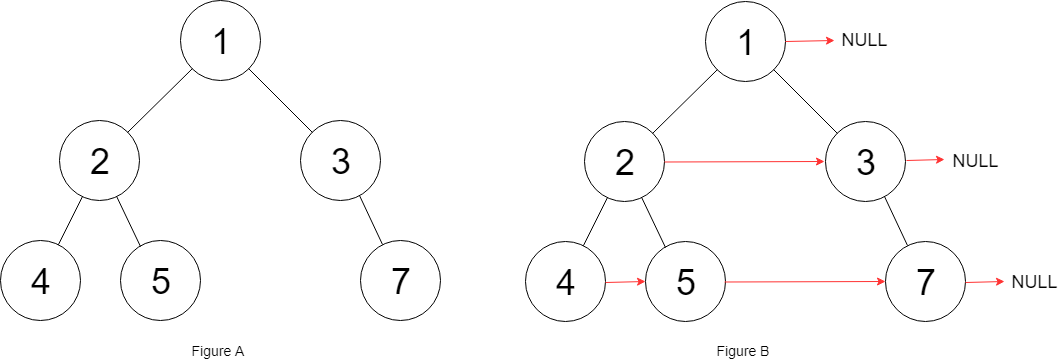
输入:{"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":null,"right":null,"val":4},"next":null,"right":{"$id":"4","left":null,"next":null,"right":null,"val":5},"val":2},"next":null,"right":{"$id":"5","left":null,"next":null,"right":{"$id":"6","left":null,"next":null,"right":null,"val":7},"val":3},"val":1}
输出:{"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":{"$id":"4","left":null,"next":{"$id":"5","left":null,"next":null,"right":null,"val":7},"right":null,"val":5},"right":null,"val":4},"next":{"$id":"6","left":null,"next":null,"right":{"$ref":"5"},"val":3},"right":{"$ref":"4"},"val":2},"next":null,"right":{"$ref":"6"},"val":1}
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如图 B 所示。
提示:
- 你只能使用常量级额外空间。
- 使用递归解题也符合要求,本题中递归程序占用的栈空间不算做额外的空间复杂度。
#include <iostream>
#include <queue>
using namespace std;
/// Using BFS
/// Time Complexity: O(n)
/// Space Complexity: O(n)
/// Definition for binary tree with next pointer.
struct Node{
int val;
Node* left, *right, *next;
Node(int x): val(x), left(NULL), right(NULL), next(NULL) {}
};
//该解法和3.3的解法没有差异
class Solution{
public:
Node* connect(Node* root){
if(!root)
return NULL;
queue<Node*> q;
q.push(root);
int level_num = 1;
while(!q.empty()){
int new_level_num = 0;
for(int i=0; i<level_num; i++){
Node* node = q.front();
q.pop();
node->next = (i == level_num - 1 ? NULL : q.front());//用来判断是否为最后一个节点
if(node->left){
q.push(node->left);
new_level_num ++;
}
if(node->right){
q.push(node->right);
new_level_num ++;
}
}
level_num = new_level_num; //用来对下一层的节点进行计数
}
return root;
}
};
二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
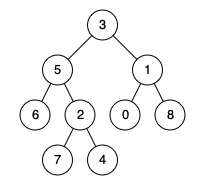
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉树中。
最近是指离叶子最近,最远公共祖先一定是根节点,无意义
#include <iostream>
#include <cassert>
using namespace std;
/// Recursion implementation
/// Time Complexity: O(n)
/// Space Complexity: O(1)
///Definition for a binary tree node.
struct TreeNode{
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x): val(x), left(NULL), right(NULL){}
};
class Solution{
public:
// 在root中寻找p和q
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q){
//底部的基本情况
if(root == NULL) // 节点为空
return root;
if(root == p || root == q) // 节点不为空,判断是否找到,无需关心是否为叶子节点
return root;
TreeNode* left = lowestCommonAncestor(root->left, p, q);
TreeNode* right = lowestCommonAncestor(root->right, p, q);
if(left != NULL && right != NULL) //且左右节点都是目标,返回自身
return root;
//自底向上,最后返回的,自身为目标节点,且另一个目标节点在其之下。
if(left != NULL) //左节点非空
return left;
if(right != NULL) //右节点非空
return right;
return NULL; //左右节点都为空
}
};
二叉树的序列化与反序列化
序列化是将一个数据结构或者对象转换为连续的比特位的操作,进而可以将转换后的数据存储在一个文件或者内存中,同时也可以通过网络传输到另一个计算机环境,采取相反方式重构得到原数据。
请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑,你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。
示例:
你可以将以下二叉树:
1
/ \
2 3
/ \
4 5
序列化为 "[1,2,3,null,null,4,5]"
提示: 这与 LeetCode 目前使用的方式一致,详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式,你也可以采用其他的方法解决这个问题。
说明: 不要使用类的成员 / 全局 / 静态变量来存储状态,你的序列化和反序列化算法应该是无状态的。
#include <iostream>
#include <vector>
#include <queue>
#include <cassert>
using namespace std;
/// BFS
/// Time Complexity: O(n)
/// Space Complexity: O(n)
/// Definition for a binary tree node.
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Codec{
public:
//Encodes a tree to a single string.
string serialize(TreeNode* root){
if(root)
return "[null]";
string ret = "[";
queue<TreeNode*> q;
q.push(root);
ret += to_string(root->val);
while(!q.empty()){
TreeNode* cur = q.front();
q.pop();
if(cur->left){
ret += "," + to_string(cur->left->val);
q.push(cur->left);
}
else
ret += ",null";
if(cur->right){
ret += "," + to_string(cur->right->val);
q.push(cur->right);
}
else
ret += ",null";
}
return ret + "]";
}
// Decodes your encoded data to tree.
TreeNode* deserialize(string data){
vector<string> vec = get_vector(data);
if(vec.size()==0 || (vec.size() == 1 && vec[0]=="nulll"))
return NULL;
TreeNode* root = new TreeNode(atoi(vec[0].c_str()));
queue<TreeNode*> q;
q.push(root);
int index = 1;
while(!q.empty()){
TreeNode* cur = q.front();
q.pop();
assert(vec.size() - index >= 2);
if(vec[index] != "null"){
cur->left = new TreeNode(atoi(vec[index].c_str()));
q.push(cur->left);
}
index ++;
if(vec[index] != "null"){
cur->right = new TreeNode(atoi(vec[index].c_str()));
q.push(cur->right);
}
index ++;
}
return root;
}
private:
vector<string> get_vector(const string& data){
string s = data.substr(1, data.size() -2) + ",";
vector<string> res;
int i = 0;
while(i < s.size()){
int comma = s.find(',', i);
res.push_back(s.substr(i, comma - i));
i = comma + 1;
}
return res;
}
};
int main() {
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->right->left = new TreeNode(4);
root->right->right = new TreeNode(5);
string s = Codec().serialize(root);
cout << s << endl;
TreeNode* x = Codec().deserialize(s);
cout << Codec().serialize(x) << endl;
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号