数据总结

队列

单调队列

P1886 滑动窗口 /【模板】单调队列

「单调」指的是元素的「规律」——递增（或递减）。

「队列」指的是元素只能从队头和队尾进行操作。

要求的是每连续的 $k$ 个数中的最大（最小）值，很明显，当一个数进入所要 "寻找" 最大值的范围中时，若这个数比其前面（先进队）的数要大，显然，前面的数会比这个数先出队且不再可能是最大值。

也就是说——当满足以上条件时，可将前面的数 "弹出"，再将该数真正 $push$ 进队尾。

这就相当于维护了一个递减的队列，符合单调队列的定义，减少了重复的比较次数，不仅如此，由于维护出的队伍是查询范围内的且是递减的，队头必定是该查询区域内的最大值，因此输出时只需输出队头即可。

显而易见的是，在这样的算法中，每个数只要进队与出队各一次，因此时间复杂度被降到了 $O(N)$。

#include <iostream>
#include <cstdio>
#include <deque>

using namespace std;

const int maxn = 1e6 + 5;
int n, m;
int a[maxn];
deque<int> q;

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    for (int i = 1; i <= n; i++)
    {
        while (!q.empty() && a[q.back()] > a[i])
            q.pop_back();
        q.push_back(i);
        if (i >= m)
        {
            while (!q.empty() && q.front() <= i - m)
                q.pop_front();
            printf("%d ", a[q.front()]);
        }
    }
    printf("\n");
    while (!q.empty())
        q.pop_back();
    for (int i = 1; i <= n; i++)
    {
        while (!q.empty() && a[q.back()] < a[i])
            q.pop_back();
        q.push_back(i);
        if(i>=m)
        {
            while(!q.empty()&&q.front()<=i-m) q.pop_front();
            printf("%d ",a[q.front()]);
        }
    }
    return 0;
}

单调队列应用场景：

单调队列（Monotonic Queue）是一种数据结构，常用于解决一些与滑动窗口相关的问题。它可以在 $O(1)$ 的时间复杂度内实现以下操作：

在队尾添加元素
在队头移除元素
获取当前队列中的最大（或最小）元素

使用单调队列的典型场景包括：

滑动窗口最大值（或最小值）问题：给定一个数组和窗口的大小，需要找到每个窗口内的最大（或最小）值。单调队列可以帮助我们在窗口滑动的过程中高效地获取最大（或最小）值。
求解滑动窗口的某种性质：有时候我们需要在滑动窗口中求解的不仅仅是最大（或最小）值，还可能是其他一些特定的性质，比如窗口内的元素之和、平均值等。通过维护一个适当的单调队列，我们可以在滑动窗口中高效地求解这些性质。
解决一些需要在固定大小的窗口中维护最大（或最小）值的问题：比如在一个数据流中，需要不断更新当前窗口的最大（或最小）值。单调队列可以帮助我们在数据流中高效地维护这些值。

P1714 切蛋糕

前置内容：P1115 最大子段和，先用两种方式解决该问题。

动态规划

code
贪心

从 $i=1$ 开始扫到 $n$ ，如果比 $ans$ 大记录答案，如果是负数则舍弃当前答案，归零继续扫描（若加到 $a_i$ 时 $sum$ 是负数，则 $sum+a_{i+1}$ 一定小于 $0+a_{i+1}$ ）。

本质上是从 dp 做法转化而来。

于是此题成为了前置题目的升级版，要求限定范围内的最大值。首先对于范围求和，使用前缀和在 $O(1)$ 时间复杂度求解，然后将问题变为：求两个位置 $l,r$ 使得 $r-l \leqslant m$ ，直接暴力显然超时。

但是对于一个固定的位置 $p$ ，对于 $1 \sim p-1$ 的满足条件最大子段和，只需找到 $p$ 前 $m$ 个数的区间中最小的 $pre_i$ ，此时 $pre_p \sim pre_i$ 就是当前的区间最大值。

维护固定长度的最值，考虑使用单调队列，维护前 $m$ 个数的最小值。时间复杂度 $\ O(n)$ 。

树状数组

P3372 【模板】线段树 1

使用树状数组解决区间修改+区间查询问题，使用到二阶树状数组，保留上一道题的差分思想，我们又有一下式子：

\[ \begin{aligned} \sum_{i=1}^{k}a_i &= \sum_{i=1}^{k} \sum_{j=1}^{i}D_j \\ &= \sum_{i=1}^{k}(k-i+1)D_i\\ &= k \sum_{i=1}^{k}D_i-\sum_{i=2}^{k-1}(i-1)D_i \\ &= k\sum_{i=1}^{k}D_i-\sum_{i=1}^{k}D_i \end{aligned}\]

即：

\[\begin{aligned}a_1+a_2+a_3+...+a_k &= D_1+(D_1+D_2)+(D_1+D_2+D_3)+...+ (D_1+D_2+D_3+...+D_k)\\ &=kD_1+(k-1)D_2+(k-2)D_3+...+(k-(k-1))D_k\\ &=k(D_1+D_2+D_3+...+D_k)-(D_2+2D_3+3D_4+...+(k-1)D_k)\\ &= k\sum_{i=1}^{k}D_i-\sum_{i=1}^{k}(i-1) D_i \end{aligned} \]

观察到公式最后一行是求两个前缀和，用两个树状数组维护，一个实现 $D_i$，一个实现 $(i-1)D_i$。

平衡树

Treap

关键点1

如果给定的键值与随机优先值确定，且两两不同，得到的 treap 是唯一确定的。

浅证：考虑对 $n$ 个二元组 $(k_i,v_i)$ 建立笛卡尔树。先将二元组以 $v_i$ 排序得到 $(k_i',v_i')$ 满足 $v_i'$ 单调递增。

那么根节点一定是 $(k_1',v_1')$，其余的 $k$ 值小于 $k_1'$ 的分离，大于 $k_1'$ 的分离建立左右子树，与原问题是一样的，由于这是一个确定的过程，根据归纳法知树也是唯一确定的。

P1486 [NOI2004] 郁闷的出纳员

treap 模板题，首先如果想要用平衡树，那么键值一定是不方便修改的，考虑引入变量 $\Delta$，一个数 $x$ 插入到平衡树中的值应为 $x-\Delta$，同时一个数能在平衡树内，当且仅当 $x \ge lower$。

接下来考虑依次对每个操作维护上述性质。

对于新建节点：比较 $x -\Delta$ 与 $lower$ 的大小决定是否插入。

对于所有人工资加 $k$ ：等价于 $lower \gets lower - k$，同时由于此次操作后新建的节点是吃不到加成的，将 $\Delta \gets \Delta +k $。

对于所有人工资减 $k$ ：与上面的操作相反。由于这个操作可能导致人退出，我们暴力删除元素，知道平衡树所有元素满足 $x\ge lower$。

对于查询第 $k$ 大：平衡树自然支持。

P3261 [JLOI2015] 城池攻占

一开始为每个人建立一个可合并数据结构，维护最大值与费用总和，自底向上维护总费用。数据结构可以用左偏树或 treap + 启发式合并或优先队列的启发式合并。

线段树

一种非常优美的数据结构。

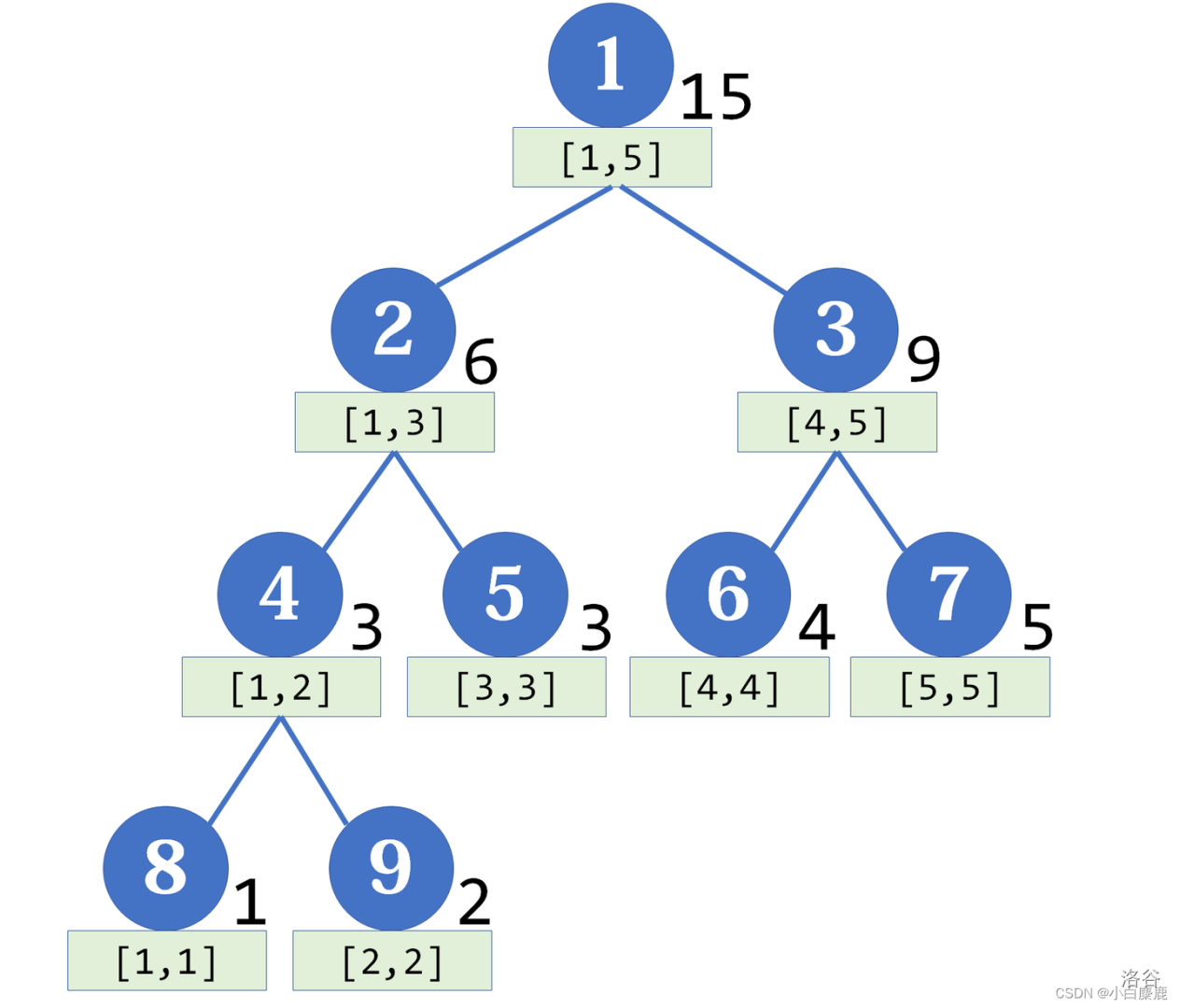
运用分治的思想，不断的将区间从中间分开成为两个子区间，通过不超过 $\log n$ 个子区间拼凑出目标区间。

树链剖分

本质上是一种思想，可以利用树的 dfs 序将树的子树转化为一段连续的区间，一段路径转化为 $\Theta(\log n)$ 个连续的 dfs 序区间。

这样，树上问题就变成了区间问题，用线段树维护即可。

可持久化线段树

主要是基于两个方面：

对于线段树单点修改，每次在线段树上最多只影响到 $\log n$ 个节点，于是考虑只新建这些节点，剩余的全部继承，即可实现可持久化。
如果维护的是可差分信息，那么线段树也是可以相加减的，这样可以通过前缀和思想得到只维护 $[l,r]$ 区间的线段树。

P3567 [POI 2014] KUR-Couriers

查询严格众数。

考虑直接建立可持久化线段树，对于询问分情况讨论：

左子树的数字个数等于右子树：一定不存在绝对众数。
返回数字更多的子树信息，因为少的一定已经严格小于了 $\frac{1}{2}$，没必要看了，多的还有可能，注意最后判断一下。

code

~~没想到多年未打主席树依然记得。~~

P3402 可持久化并查集

本质上就是可持久化数组，由于路径压缩不是单点修改，所以考虑启发式合并，将 $sz,fa$ 数组同时可持久化。

code

分块 & 莫队

严格来讲只是一种思想，也分块也可以看成一种数据结构。

分块

将序列分成很多个段，思想是小块暴力，大块整段维护，时间复杂度可以通过均值不等式计算。

#6278. 数列分块入门 2 & #6279. 数列分块入门 3

考虑对每个块维护其有序序列，这样可以二分做到快速定位。

设将序列分成了 $T$ 段，同时对每一块内排序，初始化 $\Theta(T \times \frac{n}{T} \log \frac{n}{T}) = \Theta(n \log \frac{n}{T})$。

对每个操作，最坏情况复杂度 $\Theta(\frac{n}{T} \log n + T)$。

总复杂度 $\Theta(n \log \frac{n}{T}+\frac{mn}{T}\log \frac{n}{T} + mT)$，最小 $\Theta(m \sqrt n \log n)$。

#6281. 数列分块入门 5

有一个结论，一个正整数开平方下取整，只用 $\Theta(\log \log n)$ 次就会收敛到 $1$。

考虑分块并打上 $\text{tag}$，表示这一块是否都为 $0/1$ 不用继续操作，如果没有 $\text{tag}$ 就暴力修改，时间复杂度均摊 $\Theta(n \sqrt n \log \log n)$。

#6285. 数列分块入门 9 | P4168 [Violet] 蒲公英

维护区间众数，由于不具有可加性，考虑分块。

你以为莫队只能离线？莫队的在线化改造讲得好。

预处理出两个数组：

区间答案
其他信息（本题是元素出现次数）

即维护两个辅助信息 $p_{i,j}$ 表示块 $i,j$ 之间的众数，$s_{i,j}$ 表示前 $i$ 个块中数 $j$ 出现的次数。

对于查询 $[l,r]$ 间的众数，如果在相邻块中，则暴力查询，复杂度 $\Theta(\frac{N}{T})$。

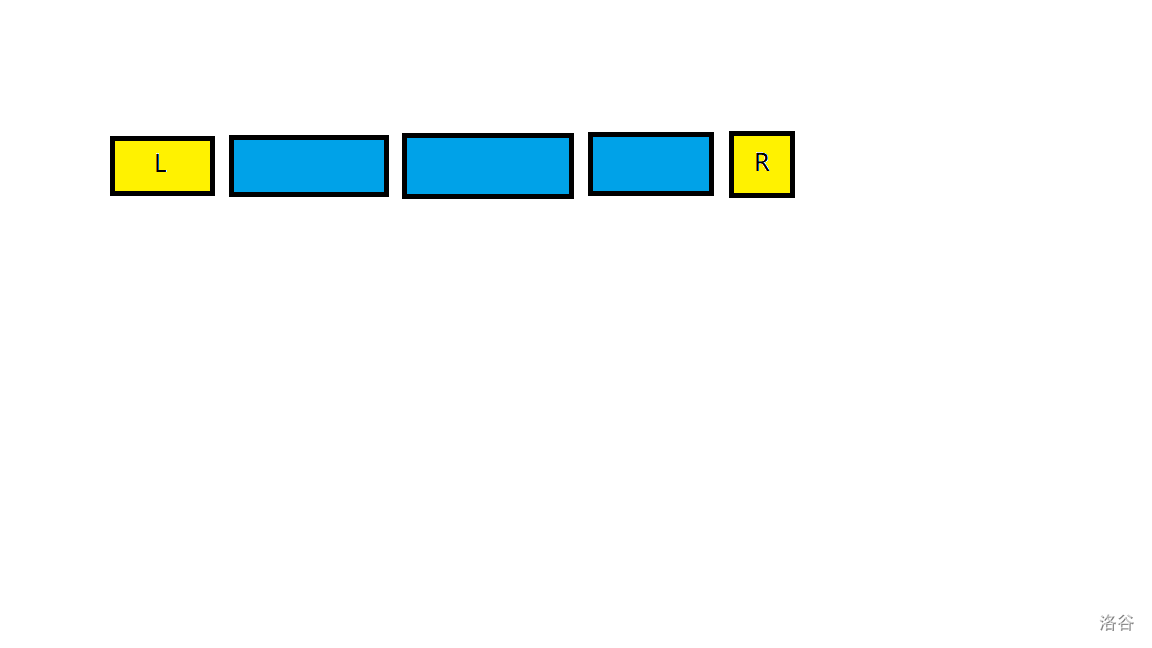
否则，如上图的情况，众数要么来自蓝色的块中，要么是黄色的散块中。我们先将答案设置为预处理出的蓝色区间中的答案。由于已经求出了蓝色区间每个数出现了多少次（根据前缀和数组 $s$ 可计算），然后考虑剩下的可能成为众数的数，暴力扫黄色区间即可。

理论可以计算出 $T = n^{\frac{1}{2}}$ 时取到最优复杂度。

code

P5048 [Ynoi2019 模拟赛] Yuno loves sqrt technology III

上面分块求区间众数的时间复杂度是 $\Theta(n \sqrt n)$，空间复杂度是 $\Theta(n \sqrt n)$。

考虑如何做到线性空间。

依然预处理 $f_{i,j}$ 表示块 $[i,j]$ 众数出现次数。

同时用 vector 保存每个值出现的位置下标，对序列中的每个数再记录他在 vector 的哪个位置。

接下来考虑询问，小范围的直接暴力做掉，先假定答案由中间的块贡献 $ans = f_{l+1,r-1}$。

剩余的两边的碎块，我们要看他们能不能成为答案。

对于左边的碎块，我们只要满足 $p_x + ans \le r$，说明 $ans+1$ 可以成为答案， $ans \gets ans+1$。

对右边同理，检查 $p_x - ans \ge l$，并不断更新答案。

时间复杂度，我们会检查 $\Theta (\sqrt n)$ 个元素，$ans$ 指针的跨越也是 $\Theta(\sqrt n)$ 的（因为两边最多 $2\sqrt n$ 个元素可以贡献答案），时间复杂度 $\Theta(n \sqrt n)$，空间复杂度 $\Theta(n)$。

P3203 [HNOI2010] 弹飞绵羊

本题的每一个节点都唯一对应了一个后继结点，故最终形成了一种树状结构。

如果只有查询操作，那么只用 $\Theta(n)$ 预处理即可回答查询，瓶颈在于修改必需得重新处理。

不妨分块，对每个块内预处理 $to_i,cnt_i$ 表示 $i$ 跳出这个块跳到了 $to_i$ 号节点，用了 $cnt_i$ 步。

这样修改时就只有一个块内的元素需要重新扫描，时间复杂度 $\Theta(n\sqrt n)$。

CF551E GukiZ and GukiZiana

简单分块，在每个块内维护一个哈希表，直接暴力查询即可。

P12685 [国家集训队] 排队加强版

我的题解

先离散化，然后考虑在线地维护这个过程。假设我们交换了 $l,r(l<r)$ 两个位置，那么它对答案的影响就是：

\[(-1)^{[h_l > h_r]} - \sum_{i=l+1}^{r-1}[h_i< h_l] - \sum_{i=l+1}^{r-1} [h_i > h_r] + \sum_{i=l+1}^{r-1} [h_i < h_r] + \sum_{i=l+1}^{r-1} [h_i>h_l] \]

发现这是求区间排名问题。

同时交换操作需要我们支持单点修改。

这是一个经典的树套树问题，可以采用树状数组套线段树或者线段树套平衡树，这里采用简洁的分块套树状数组。

时间复杂度 $\Theta(n \sqrt n \log n)$。

Chef and Churu

区间和套区间和的问题，我们可以很轻松对 $a$ 进行维护，可是对于函数的序列，一次修改会影响到多个函数且函数之间没有关系，不好上数据结构，故考虑分块。

设块长为 $T$，我们预处理每个块中序列元素的出现次数，可以用差分做区间加，时间复杂度 $\Theta(\frac{N}{T} \times (T+N)) = \Theta(\frac{N^2}{T} + N)$。

然后求出每个块内函数值之和，复杂度也是 $\Theta(\frac{N^2}{T})$。

然后考虑查询，散块的直接扫，整段的和已经求出，不妨用树状数组维护原数组，时间复杂度 $\Theta(T \log N)$。

对应地，修改的时间复杂度为 $\Theta(\log N + \frac{N}{T})$。

总时间复杂度 $\Theta(\frac{N^2}{T} + N(T\log N + \frac{N}{T})) = \Theta(\frac{N^2}{T} + N T\log N)$。

由均值不等式，当且仅当 $\frac{N^2}{T} = NT\log N$ 时取最小值，即 $T=\sqrt \frac{N}{\log N}$ 时，理论最优复杂度为 $\Theta(n \sqrt n \log n)$。

$\text{upd:}$ 可以将树状数组替换为分块，分块维护前缀和，这样单点改为 $\Theta(\sqrt n)$，区间查为 $\Theta(1)$。总复杂度降到 $\Theta(n \sqrt n)$。

值域分块

顾名思义就是在值域上分块，在一些情况下用于替代线段树或树状数组以获得更优复杂度。

我们发现对于区间修改，区间查询，分块的修改和查询时间复杂度都是 $\Theta(\sqrt n)$。

对于单点修改，区间查询，可以做到修改 $\Theta(1)$，查询 $\Theta(\sqrt n)$。

相比树状数组的 $\Theta(\log n)$，在修改远多于查询时，我们可以用 $\Theta(1)$ 的操作均摊掉复杂度，使得最终复杂度为 $\Theta(\sqrt n)$ 而不是 $\Theta(\sqrt n \log n)$。

P4867 Gty的妹子序列

考虑莫队，使用树状数组维护是 $\Theta(n \sqrt n \log n)$ 的，将树状数组用值域分块替换，由于更少的查询操作，时间复杂度变为 $\Theta(n \sqrt n)$。

莫队

本质上还是一种暴力，但是通过离线使得暴力移动的次数有了保障。

SP3267 DQUERY - D-query

按照块的 $\text{id}$ 排序，如果在同一个块内，则按照右端点排序。

对于一个块内的询问，右端点最多移动 $\Theta(n)$ 次，左端点最多移动 $\Theta(\sqrt n)$次。

一共有 $\sqrt n$ 个块，复杂度 $\Theta(n\sqrt n)$。

对于相邻两块之间的移动，最多移 $\Theta(n)$ 次，一共移 $\Theta(n \sqrt n)$ 次。

总复杂度 $\Theta(n \sqrt n)$。

P1903 [国家集训队] 数颜色 / 维护队列

带修莫队板子。

考虑给移动的指针加上时间维度，对于每一次修改操作建立时间戳。

code

注意到有一个 trick，由于一个值要反复正着改，反着改，不妨直接交换对应数值，省去记录原值的码量。

SP10707 COT2 - Count on a tree II

树上莫队板子。

主要思想是利用括号序将树上的信息转化到序列上利用莫队统计答案。

括号序的求法：dfs 的过程中入队的时候记录一次节点编号，出队的时候再记录一次。

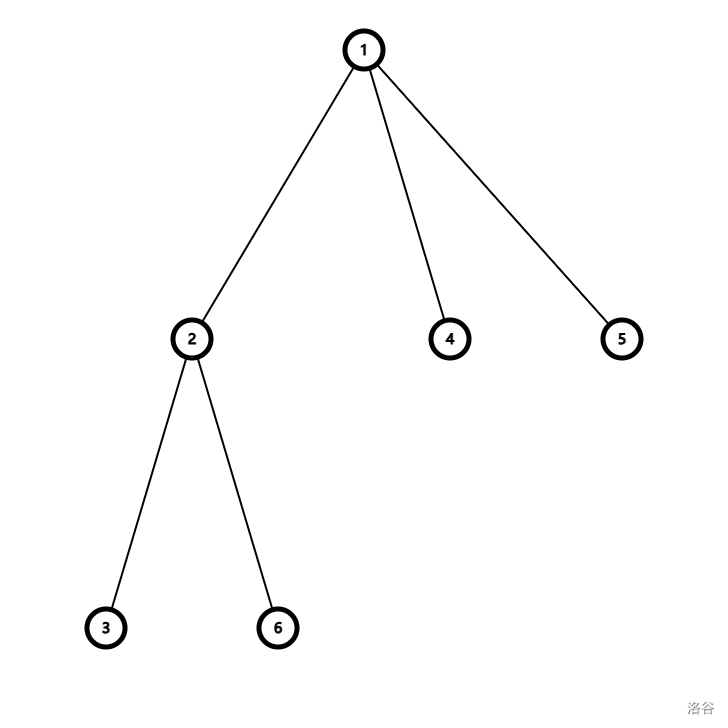
这棵树的括号序就是：1 2 3 3 6 6 2 4 4 5 5 1。

容易发现一个性质：记一个节点进入时的下标为 $in_u$，结束时下标为 $out_u$，那么在 $in_u$ 与 $out_u$ 之间的都是 $u$ 的子树。

接下来考虑用括号序序列 $a$ 表示路径 $u \rightsquigarrow v$。

$u,v$ 有祖先关系。

结论：取 $a$ 的 $[in_u,in_v]$ 且 $in_u< in_v$。

举例：路径 $1\rightsquigarrow 6$，则取括号序 1 2 3 3 6。
不难观察到，路径上的点只出现了一次，而出现了两次的必定在 $v$ 的子树中，直接忽略其贡献即可。
$u,v$ 无祖先关系。

结论：取 $a$ 的 $[out_u,in_v]$ 且 $out_u< in_v$，同时要单独考虑 $lca_{u,v}$ 的影响。

举例：路径 $3\rightsquigarrow 4$，则取括号序 3 6 6 2 4，同时要加入 $lca_{3,4}=1$。

证明：假设 $lca_{u,v} = w$，如下图。

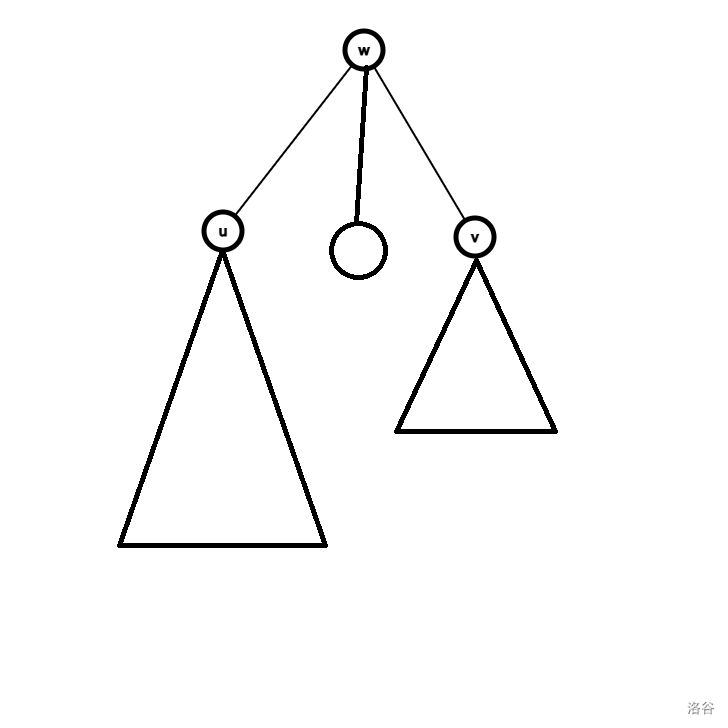
从 $ed_u$ 开始截取，那么此时 dfs 开始回溯，路径 $u \rightsquigarrow w$ 上的点在 $s$ 只出现一次，且不包括 $w$。对于路径 $w \rightsquigarrow v$ 上的点，也仅会出现一次，且不包括 $w$。

对于 $w$ 的其他子树，节点会恰好出现两次，可以直接忽略其贡献。

最后除了 $w$ 其他路径上的节点都被统计，只用单独处理 $w$ 的影响即可。

综上，树上的每条路径都对应了长度为 $2n$ 的括号序上的一段区间（也可以是一段区间加上一个单点）。直接离线下来莫队即可。

AT_joisc2014_c 歴史の研究

回滚莫队/不删除莫队板子。

此题要求维护的信息是类似区间最大值，那么普通莫队当缩短区间时计算答案就出现了瓶颈：如果在删除时将区间最大值删掉了，我们不知道区间次小值，只能暴力找答案，同理，找次次小值时也要重新更新。

就这样，移动一次指针的复杂度变为了 $\Theta(n)$，不能接受。

观察到加入一个点更新答案是很容易的，那么有没有一种方法能够不做删除操作只是插入，这就是回滚莫队的基本思想。

先按照普通莫队的方法排序，注意不能使用奇偶块优化，保证右端点单调递增。

我们依次考虑每个左端点对应块中的询问。

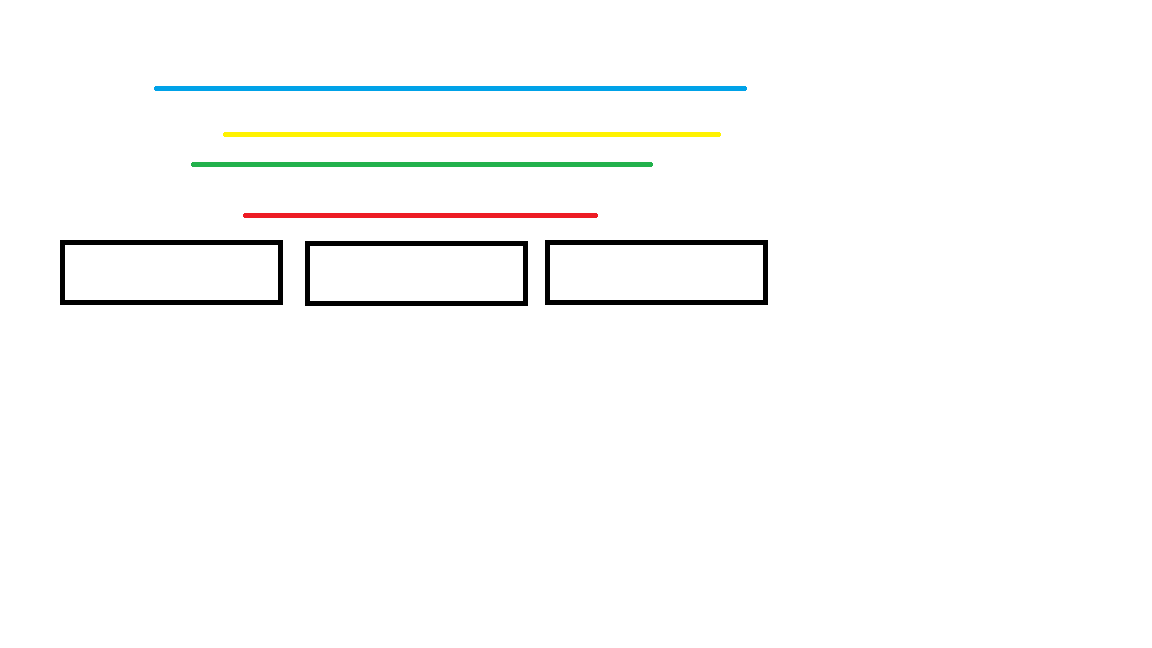
如图，每条线都代表了一个询问区间。回滚莫队按照一下方式处理询问：

对于左右端点在同一块内的询问，提前暴力做掉，保证询问的右端点总是跨区间的。
将当前区间 $l \gets ed_{bel_l},r\gets l-1$，表示一段空区间。
将当前答案置为 $lst$，即左端点还在原位置的答案。
移动 $r$ 指针。
将 $lst$ 置为当前答案，描述左端点未移动的区间。
移动左端点更新答案，最后再删除贡献。

一个块处理完后，清空桶后处理下一个块。

复杂度 $l$ 指针一个块移动 $\sqrt n$ 次，$r$ 移动 $n$ 次，总复杂度 $\Theta(n \sqrt n)$。

P4137 Rmq Problem / mex

只删不增莫队板子题。

观察到我们对于一个集合 $S$，删除其中的元素后求 $\text{mex}$ 比插入是更容易的。所以将回滚莫队的初始区间设为一个极大的区间即可。

code

带修莫队 / 分块

U573250 强制在线寂寂寞寞队

首先考虑没有询问怎么做，显然采用上面的分块思想，记录 $f_{i,j}$ 表示 $[i,j]$ 块的答案，$s_{i,j}$ 表示前 $i$ 个块中 $j$ 出现的次数。

没有修改就 $\Theta(n \sqrt n)$ 做完了。

现在有了修改操作，不妨参考线段树懒标记的思想，我们改了一个位置 $p$，这表示跟 $p$ 的块有关的答案都失效了（但是我们可以更新 $s$ 数组，复杂度是可以接受的），那么我们可以对 $f$ 数组记录时间戳代表他的更新时间，不做真正的更新。

在询问时，同一块内的暴力扫掉，在不同块时，我们要先得到中间块的答案辅助转移，所以我们只需要考虑当前时间与时间戳时间的修改，先复原出原来的 $cnt$ 数组，然后考虑修改的影响。

这样就得到了临近整块的答案，最后的碎块暴力扫掉即可。

时间复杂度 $\Theta(n^{\frac{5}{3}})$。

code

~~在线莫队出处写的代码为了像莫队而太冗长了。~~

LCT

困难。

扫描线

面积类

序列类

P10814 【模板】离线二维数点

板子题。

计算 $\sum_{i=l}^{r} [a_i \le k]$。

以序列位置 $i$ 为 $x$ 轴，值域为 $y$ 轴建立平面直角坐标系。

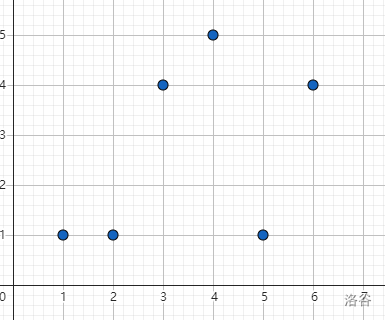
然后将答案差分转化为在 $l-1,r$ 两个点的询问，即$\sum_{i=1}^{r} [a_i \le k] - \sum_{i=1}^{l-1} [a_i \le k]$。

这样我们假设有一根线，并且我们用树状数组维护它，让它从左向右扫描，扫到一个数就加到树状数组上，这样就可以 $\Theta(\log n)$ 求出每个询问。

时间复杂度 $\Theta(n \log n)$

P1972 [SDOI2009] HH的项链

考虑建立扫描线模型。

我们想要不重不漏地统计到每个数的贡献，就得建立一个标准，使其被正确计算。

不放认为在一段区间 $[l,r]$ 中如果出现一个数 $a$，我们只认首次出现的 $a_i$，对于如何刻画首次出现，可以考虑 $a_i$ 前面的 $a_i$ 出现的位置，记为 $lst_i$，如果 $a_i$ 首次出现，应有 $lst_i < l$，如果 $a_i$ 前面没有相同的数值不妨认为 $lst_i = 0$。

这样一个区间的答案就是 $\sum_{i=l}^{r} [lst_i < l]$。

建立 $i$ 为 $x$ 轴，$lst$ 为 $y$ 轴的平面直角坐标系，问题就转化为扫描线模板。

P3755 [CQOI2017] 老C的任务

离线二维数点板子。

C. World of Darkraft: Battle for Azathoth

初始时已经给定了偏序关系，考虑创建一个数值的扫描线，横轴维护防御，纵轴维护攻击，沿着 $x$ 轴扫，相当于枚举防具，然后不断地碰到怪兽。

纵向开一个线段树表示选取攻击力为 $i$ 的武器时能获得的最大收益，那么碰到一个怪物相当于值域在 $(y_k,+ \infty )$ 武器收益增加 $z_k$，然后求最大值减去当前防具的代价就是当前的答案。

code

posted @ 2025-04-09 20:25 vanueber 阅读(26) 评论(0) 收藏举报

刷新页面返回顶部

ber!

队列

单调队列

树状数组

平衡树

Treap

关键点1

线段树

树链剖分

可持久化线段树

分块 & 莫队

分块

#6278. 数列分块入门 2 & #6279. 数列分块入门 3

#6285. 数列分块入门 9 | P4168 [Violet] 蒲公英

值域分块

莫队

带修莫队 / 分块

LCT

扫描线

面积类

序列类

公告