快速傅里叶变换总结
基本概念
对于求和式 \(\sum a_ix^i\)，如果是有限项相加，称为多项式，记作
\[f(x)=\sum_{i=0}^n a_ix^i。
\]
其中最高次项的次数为 \(n\)，为 \(n\) 次多项式。
用 \(n+1\) 个点可以唯一地确定一个 \(n\) 次多项式，这一过程可以参考 拉格朗日插值。
引入
给定多项式 \(f(x),g(x)\)，求 \(f(x)\cdot g(x)\)各项系数。
通过系数表达式直接乘时间复杂度 \(\Theta(n^2)\)，但考虑两个函数的一组点值表达式
\[(x_1,f(x_1))\cdots(x_k,f(x_k))\\
(x_1,g(x_1))\cdots(x_k,g(x_k))
\]
此时两者相乘的点值表达式可以在 \(\Theta(n)\) 的时间求出。
即:
\[(x_1,f(x_1)\cdot g(x_1))\cdots(x_k,f(x_k)\cdot g(x_k))
\]
于是就有想法：将系数表达式 \(\Rightarrow\) 点值表达式，点值相乘后 \(\Rightarrow\) 系数表达式。
快速傅里叶变换就是完成中间过程的工具，可以在 \(\Theta(n \log n)\) 的时间完成系数表示与点值表示的转换。
前置知识
有以下重要知识
欧拉公式：
\[\mathrm{e}^{\mathrm{i}x}=\cos x+\mathrm{i}\sin x
\]
单位复数根：
\[\begin{aligned}
\omega_n^k&= \cos \frac{2 \pi k}{n} + \mathrm{i} \sin \frac{2 \pi k}{n} \\
\omega_n^n&=1\\
\omega_n^k&=\omega_{2n}^{2k}\\
\omega_{2n}^{k+n}&=-\omega_{2n}^k\\
\end{aligned}
\]
快速傅里叶变换
将多项式 \(f(x)=\sum_{i=0}^{n}a_ix^i\) 按照下标为奇偶数划分为两个多项式
\[G(x)=a_0+a_2{x^1}+a_4{x^2}+\dots+a_{n-2}x^{\frac{n}{2}-1}\\
H(x)=a_1+a_3{x}+a_5{x^2}+ \dots+a_{n-1}x^{\frac{n}{2}-1}\]
有：
\[f(x)= G(x^2) + xH(x^2)
\]
代入两组值得到：
\[\begin{aligned}
f(\omega_n^k) &= G((\omega_n^k)^2) + \omega_n^k \times H((\omega_n^k)^2) \\
&= G(\omega_n^{2k}) + \omega_n^k \times H(\omega_n^{2k}) \\
&= G(\omega_{n/2}^k) + \omega_n^k \times H(\omega_{n/2}^k)
\end{aligned}
\\
\begin{aligned}
f(\omega_n^{k+n/2}) &= G(\omega_n^{2k+n}) + \omega_n^{k+n/2} \times H(\omega_n^{2k+n}) \\
&= G(\omega_n^{2k}) - \omega_n^k \times H(\omega_n^{2k}) \\
&= G(\omega_{n/2}^k) - \omega_n^k \times H(\omega_{n/2}^k)
\end{aligned}
\]
发现只要求出 \(G(\omega_n^{2k}),H(\omega_{n/2}^k)\) 的值就可以同时求得 \(f(\omega_n^k),f(\omega_n^{k+n/2})\) 的值。
并且这个问题跟原问题是相同的。
于是分治下来解决子问题，最后合并为原问题即可。
void FFT(comp f[],int n)
{
if(n==1) return;
comp f1[n/2],f2[n/2];
for(int i=0;i<n/2;++i)
{
f1[i]=f[i<<1],f2[i]=f[i<<1|1];
}
FFT(f1,n/2),FFT(f2,n/2);
comp w=polar(1.0,(2.0*pi/n)),wk=comp(1,0);
for(int i=0;i<n/2;++i)
{
f[i]=f1[i]+f2[i]*wk;
f[i+n/2]=f1[i]-f2[i]*wk;
wk*=w;
}
}
快速傅里叶逆变换
现在完成了系数表示法 \(\Rightarrow\) 点值表示法的过程，现在考虑逆向转换。
有结论：
IFFT等价于 FFT 中代入得复数变为其倒数，再除以变换长度。
故结论成立。
容易证明，这也等价于将\(\{y_0,y_1,y_2,\cdots,y_{n-1}\}\) 做 FFT 变换后除以 \(n\)，再反转后 \(n - 1\) 个元素。
优化
以上的代码实现都基于递归，常数较大。
基于以下观察，可以写出迭代写法。
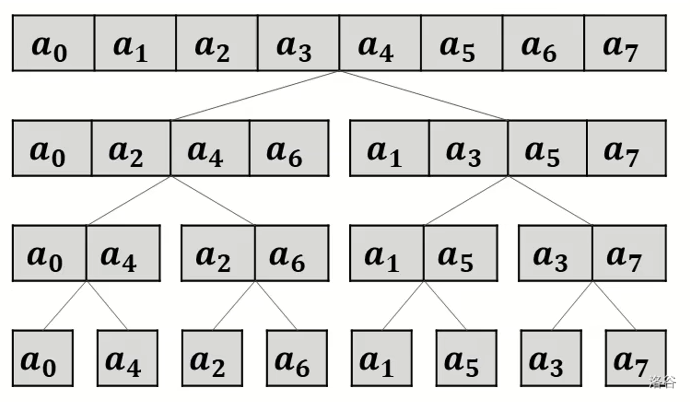
原位置对应元素的下表二进制翻转后，成了最后当前元素的下标，于是这样处理之后直接自底向上合并即可。
代码
递归版本
#include <bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
inline int read()
{
int w=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
w=(w<<1)+(w<<3)+(ch^48);
ch=getchar();
}
return w*f;
}
inline void write(int x)
{
if(x<0)
{
putchar('-');
x=-x;
}
if(x>9) write(x/10);
putchar(x%10+'0');
}
#define comp complex<double>
const int maxn=2e6+10;
const double pi=3.1415926535;
void FFT(comp f[],int n)
{
if(n==1) return;
comp f1[n/2],f2[n/2];
for(int i=0;i<n/2;++i)
{
f1[i]=f[i<<1],f2[i]=f[i<<1|1];
}
FFT(f1,n/2),FFT(f2,n/2);
comp w=polar(1.0,(2.0*pi/n)),wk=comp(1,0);
// comp w=comp(cos(2.0*pi/n),type*sin(2.0*pi/n)),wk=comp(1,0);
for(int i=0;i<n/2;++i)
{
f[i]=f1[i]+f2[i]*wk;
f[i+n/2]=f1[i]-f2[i]*wk;
wk*=w;
}
}
void IFFT(comp f[],int n)
{
FFT(f,n);
reverse(f+1,f+n);
}
int n,m;
comp a[maxn<<1],b[maxn<<1];
int main()
{
#ifndef ONLINE_JUDGE
//freopen("in.txt","r",stdin);
#endif
n=read(),m=read();
for(int i=0;i<=n;++i) a[i]=comp(read(),0);
for(int i=0;i<=m;++i) b[i]=comp(read(),0);
int k=1;
while(k<=n+m) k<<=1;
// cout<<k<<endl;
FFT(a,k),FFT(b,k);
for(int i=0;i<=k;++i)
{
a[i]*=b[i];
}
IFFT(a,k);
for(int i=0;i<=n+m;++i)
{
cout<<(int)(a[i].real()/k+0.5)<<" ";
}
return 0;
}
迭代版本
#include <bits/stdc++.h>
using namespace std;
inline int read()
{
int w=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9')
{
w=(w<<1)+(w<<3)+(ch^48);
ch=getchar();
}
return w*f;
}
void write(int x)
{
if(x<0) x=-x;
if(x>9) write(x/10);
putchar(x%10+'0');
}
#define comp complex<double>
const double pi=acos(-1);
const int maxn=4e6+10;
int n,m,len,k;
int rev[maxn];
comp a[maxn],b[maxn];
int get(int x)
{
int res=0;
for(int i=0;i<len;++i)
{
res+=(x>>i&1)<<(len-i-1);
}
return res;
}
void fft(comp f[],int n)
{
for(int i=0;i<n;++i)
{
rev[i]=get(i);
if(i<rev[i]) swap(f[i],f[rev[i]]);
}
for(int h=2;h<=n;h<<=1)
{
comp w=polar(1.0,2.0*pi/h);
for(int i=0;i<n;i+=h)
{
comp wk=comp(1,0);
for(int j=0;j<h/2;++j)
{
comp x=f[i+j],y=f[i+j+h/2]*wk;
f[i+j]=x+y,f[i+j+h/2]=x-y;
wk*=w;
}
}
}
}
void ifft(comp f[],int n)
{
fft(f,n);
reverse(f+1,f+n);
}
int main()
{
n=read(),m=read();
for(int i=0;i<=n;++i) a[i]=read();
for(int i=0;i<=m;++i) b[i]=read();
k=1;
while(k<=n+m) k<<=1,++len;
fft(a,k),fft(b,k);
for(int i=0;i<=k;++i) a[i]*=b[i];
ifft(a,k);
for(int i=0;i<=n+m;++i) printf("%d ",(int)(a[i].real()/k+0.5));
return 0;
}
解释：蝶形变换的位置数组有 \(\Theta(n)\) 的解法，但考虑 FFT 的瓶颈不在此，暴力的写法也是可行的。
浙公网安备 33010602011771号