dp重修

区间 dp

枚举断点型

dp 的状态表示设计为一段区间，一般为 \(dp_{l,r}\) 为区间 \([l,r]\) 中的答案。

状态转移时，一般按照 \(len\) 扩展答案，更新状态 \(dp_{l,r}\) 时考虑分割成两个区间的答案。

即枚举断点 \(k\)，结合 \(dp_{l,k},dp_{k+1,r}\) 的区间信息拼出 \(dp_{l,r}\) 的信息。

P3146 [USACO16OPEN] 248 G

套路题，\(dp_{l,r}\) 表示 \([l,r]\) 的最大数字，显然有转移：

\[dp_{l,r}=dp_{l,k}+1(dp_{l,k}=dp_{k+1,r}) \]

イウィ

依然套路题，用 \(dp_{l,r}\) 表示区间 \([l,r]\) 最多删去的字符数。

有如下转移：

\[dp_{l,r}=dp_{l,k}+dp_{k+1,r} \]

特别地，如果有：

且 \(\dots\) 中都被消除，即 \(dp_{l+1,k-1}=k-1-(l-1)+1 \wedge dp_{k+1,r-1}=(r-1)-(k+1)+1\)。

此时答案为 \(r-l+1\)。

最后答案即为 \(\frac{dp_{1,n}}{3}\)。

区间贡献/答案统计型

状态设计一般为区间的答案，可以考虑根据已知的信息逐步递推。

Coloring Brackets

考虑状态 \(dp_{l,r,x,y}\) 表示区间 \([l,r]\) 的左端点染色 \(x\)，右端点染色 \(y\) 的方案数。

此时根据区间长度划分递推不太好做，可以使用记忆化搜索。

考虑当前处理区间 \([l,r]\)。

1. 若 \(r=l+1\)，有 \(dp_{l,r,0,1}=dp_{l,r,0,2}=dp_{l,r,1,0}=dp_{l,r,2,0}=1\)
2. 若 \(match_l \not = r\)，即形如 \((\dots)(\dots \dots)\) 的情况，递归处理两个括号后，答案即为两者乘积。
3. 若 \(match_l = r\)，即形如 \(((\dots)\dots(\dots))\) 的情况，有转移 \(dp_{l,r,lc1,rc1}=\sum dp_{l+1,r-1,lc2,rc2}\)。

注意颜色判断，代码呼之欲出。

P8675 [蓝桥杯 2018 国 B] 搭积木

设计状态 \(dp_{k,l,r}\) 表示在第 \(k\) 层的 \([l,r]\) 填充满积木的方案数。

首先有一个 trick，判断 \([l,r]\) 是否能合法地充满积木，可以对该层求前缀和( \(1\) 代表 \(\text{X}\) )，那么

\[[l,r]\text{合法} \iff pre_r-pre_{l-1}=0 \]

然后，设计 dp 状态：

初始状态：关于 \(dp_n\) 的初始值，即第一层的状态。

状态转移：

\[dp_{i,l,r}=\sum_{x=1}^{l}\sum_{y=r}^{m}dp_{i+1,x,y} \]

最终答案：

\[1+\sum_{i=1}^{k}\sum_{j=1}^{m}\sum_{k=j}^{m}dp_{i,j,k} \]

时间复杂度 \(\Theta(mn^4)\)，考虑优化。

观察到状态转移的式子中是一个二维区间和，使用前缀和优化。

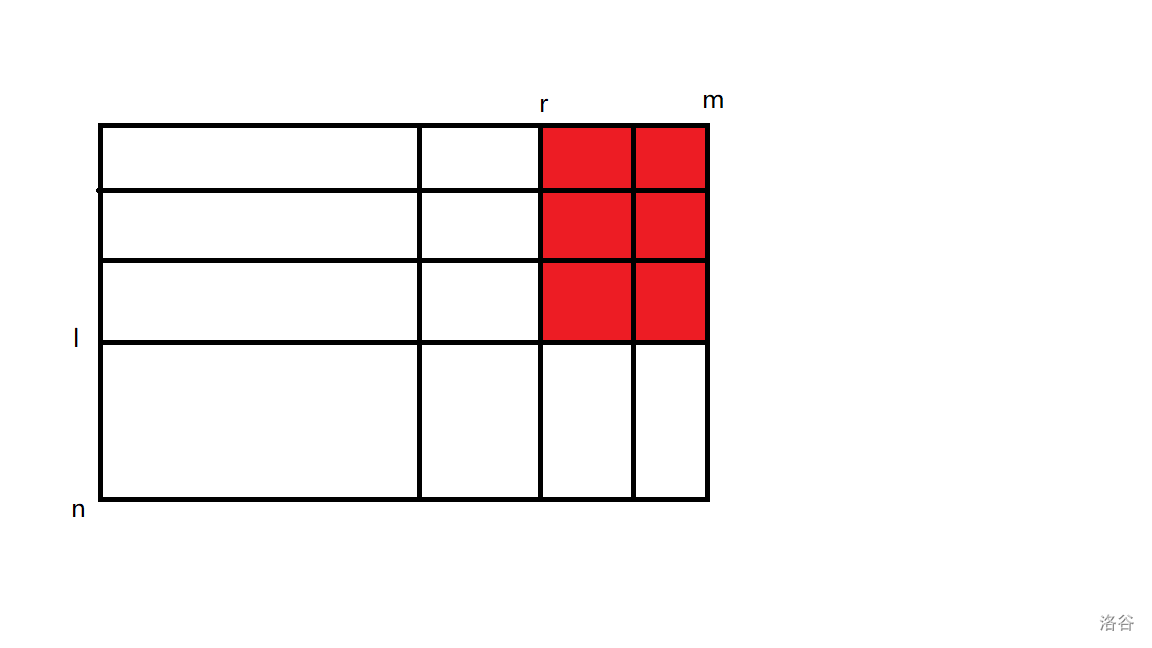
时间复杂度 \(\Theta(n^2m)\)，可以通过。

关于此题一些解释：

1. 状态计算从何而来：考虑该层的基座如何覆盖 \([l,r]\)，如果基座满足 \([l,r]\subseteq[l',r']\)，那么基座的每一个方案都能对当前区间的答案做贡献。
2. 答案为什么是上式：考虑以第 \(k\) 层为顶端的情况，所有的 \(dp_{k,l,r}\) 都能贡献答案，最后加上一个不放的情况。

dp 做题

[ABC207E] Mod i

将序列分成若干段，使得第 \(i\) 段的所有数之和为 \(i\) 的倍数的方案数。

分析

设计出普通的 dp。

令 \(dp_{i,j}\) 表示处理到第 \(i\) 个点，将序列分为 \(j\) 个序列的总方案数。

有以下转移：

\[dp_{i,j}=\sum_{k=0}^{i-1}[j \mid \sum_{p=k+1}^{i} a_p]dp_{k,j-1} \]

这相当于枚举上一个断点 \(k\) 来转移（特别地 \(k=0\) 表示前面没有断点）。

有边界条件

\[dp_{0,0} =1 \]

答案

\[\sum_{i=1}^{n} dp_{n,i} \]

这样做时间复杂度 \(\Theta(n^3)\)。

const int mod=1e9+7;
const int maxn=3005;
int n,a[maxn],dp[maxn][maxn],pre[maxn];
int query(int l,int r)
{
	return pre[r]-pre[l-1];
}
//到位置i分成了j段,i分到第j段 
//dp[i][j]=dp[1][j-1]+dp[2][j-1]+...+dp[i-1][j-1],(a[k-1]+...+a[i])%j=0 

signed main()
{
#ifndef ONLINE_JUDGE
#define LOCAL
//	freopen("in.txt","r",stdin);
#endif
	n=read();
	for(int i=1;i<=n;++i)
	{
		a[i]=read();
		pre[i]=pre[i-1]+a[i];
//		pre[i]%=mod;
	}
	dp[0][0]=1;
	for(int i=1;i<=n;++i)
	{
		for(int j=1;j<=i;++j)
		{
			for(int k=0;k<=i-1;++k)
			{
				if(query(k+1,i)%j==0)
				{
					dp[i][j]+=dp[k][j-1];
					dp[i][j]%=mod;
				}
			}
		}
	}
	int ans=0;
	for(int j=1;j<=n;++j)
	{
		ans+=dp[n][j];
		ans%=mod;
	}
	cout<<ans<<endl;
#ifdef LOCAL
	fprintf(stderr,"%f\n",1.0*clock()/CLOCKS_PER_SEC);
#endif
	return 0;
}

考虑优化，观察到

1. \(j\) 只跟前一个状态有关，可以先枚举 \(j\)。
2. 记前缀和为 \(pre\)，转移条件 \(pre_i-pre_k \equiv 0 \pmod j\) 等价于 \(pre_i \equiv pre_k \pmod j\)。
3. 每次 \(dp\) 第一位考虑的都是当前 \(i\) 的前缀。

于是开一个桶记录贡献，每次有

\[val_{pre_{i-1} \bmod j} + dp_{i-1,j-1} \]

直接转移

\[dp_{i,j}=val_{pre_i \bmod j} \]

时间复杂度 \(\Theta(n^2)\)。

const int mod=1e9+7;
const int maxn=3005;
int n,a[maxn],dp[maxn][maxn],pre[maxn];
int query(int l,int r)
{
	return pre[r]-pre[l-1];
}
//到位置i分成了j段,i分到第j段 
//dp[i][j]=dp[1][j-1]+dp[2][j-1]+...+dp[i-1][j-1],(a[k]+...+a[i])%j=0 

signed main()
{
#ifndef ONLINE_JUDGE
#define LOCAL
//	freopen("in.txt","r",stdin);
#endif
	n=read();
	for(int i=1;i<=n;++i)
	{
		a[i]=read();
		pre[i]=pre[i-1]+a[i];
//		pre[i]%=mod;
	}
	dp[0][0]=1;
	for(int j=1;j<=n;++j)
	{
		map<int,int> val;
		for(int i=1;i<=n;++i)
		{
			val[pre[i-1]%j]+=dp[i-1][j-1];
			val[pre[i-1]%j]%=mod;
			dp[i][j]+=val[pre[i]%j];
		}
	}
	int ans=0;
	for(int j=1;j<=n;++j)
	{
		ans+=dp[n][j];
		ans%=mod;
	}
	cout<<ans<<endl;
#ifdef LOCAL
	fprintf(stderr,"%f\n",1.0*clock()/CLOCKS_PER_SEC);
#endif
	return 0;
}