用根心定理证明牛顿定理三

引理：等腰梯形的四个顶点共圆。

易证。

牛顿定理三：四边形 \(A_1 A_2 A_3 A_4\) 与其内切圆的四个切点分别为 \(B_1,B_2,B_3,B_4\)，证明：\(A_1 A_3,A_2 A_4,B_1 B_3,B_2 B_4\) 四线共点。

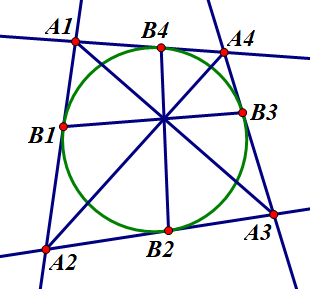
证明：在直线 \(A_1 A_2\) 上取两个点 \(P_1,P_2\)，在直线 \(A_2 A_3\) 上取两个点 \(P_3,P_4\)，在直线 \(A_3 A_4\) 上取两个点 \(P_5,P_6\)，在直线 \(A_4 A_1\) 上取两个点 \(P_7,P_8\)，使得：

\[\begin{align*} B_1 P_1=B_1 P_2\\ =B_2 P_3=B_2 P_4\\ =B_3 P_5=B_3 P_6\\ =B_4 P_7=B_4 P_8 \end{align*} \]

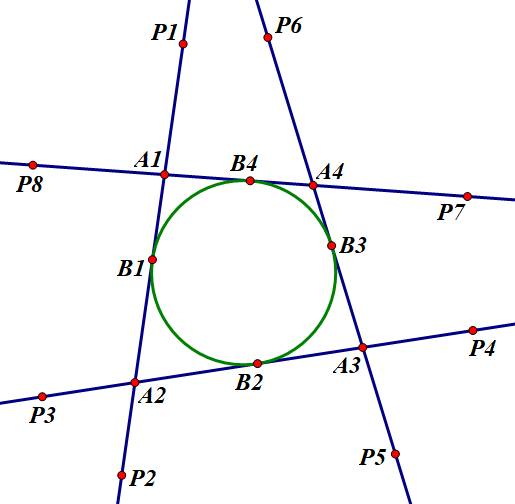
由平行线分线段成比例的逆定理，得：

\[\begin{align*} P_1 P_6 \parallel B_1 B_3 \parallel P_2 P_5\\ P_7 P_4 \parallel B_4 B_2 \parallel P_8 P_3 \end{align*} \]

故有四个等腰梯形：\(P_1 P_6 B_3 B_1,B_1 B_3 P_5 P_2,P_7 P_4 B_2 B_4,B_4 B_2 P_3 P_8\)。由引理，这些等腰梯形的四个顶点共圆。

考察圆 \(P_1 P_6 B_3 B_1\) 与圆 \(P_7 P_4 B_2 B_4\)，简记为圆 \(\alpha\) 与圆 \(\beta\)：

其中圆 \(\alpha\) 与原内切圆的根轴为 \(B_1 B_3\)，圆 \(\beta\) 与原内切圆的根轴为 \(B_4 B_2\)。

由切线长定理与 \(B_1 P_1=B_2 P_4\)，可得 \(A_2\) 关于圆 \(\alpha\) 的幂 \(A_2 B_1 \cdot A_2 P_1\) 等于 \(A_2\) 关于圆 \(\beta\) 的幂 \(A_2 B_2 \cdot A_2 P_4\)。故 \(A_2\) 在圆 \(\alpha\) 与圆 \(\beta\) 的根轴上。

同理可得 \(A_4\) 也在圆 \(\alpha\) 与圆 \(\beta\) 的根轴上。所以 \(A_2 A_4\) 即为圆 \(\alpha\) 与圆 \(\beta\) 的根轴。

由根心定理，圆 \(\alpha\)、圆 \(\beta\)、原内切圆的三条根轴 \(B_1 B_3,B_4 B_2,A_2 A_4\) 共点。

同理考察圆 \(\alpha\) 与圆 \(B_4 B_2 P_3 P_8\)，可得 \(B_1 B_3,B_4 B_2,A_1 A_3\) 共点。

故 \(A_1 A_3,A_2 A_4,B_1 B_3,B_2 B_4\) 四线共点。证毕。