“图像的手绘效果”实例分析

from PIL import Image
import numpy as np

a = np.asarray(Image.open('C:\\Users\\Public\\Pictures\\Saved Pictures\\structure.jpg'))

depth = 10.                    #浮点数，预设深度为10
grad = np.gradient(a)          #取图像灰度的梯度值
grad_x，grad_y = grad          #分别取横纵图像梯度值
grad_x = grad_x*depth/100.
grad_y = grad_y*depth/100. #根据预设深度调整图像梯度值，除以100 进行归一化
A = np.sqrt(grad_x**2 + grad_y**2 + 1.) #构造x和y梯度的三维归一化单位坐标系
uni_x = grad_x/A
uni_y = grad_y/A
uni_z = 1./A

vec_el = np.pi/2.2            #光源的俯视角度，弧度值
vec_az = np.pi/4.             #光源的方位角度，弧度值
dx = np.cos(vec_el)*np.cos(vec_az)  #光源分别对x y z三个轴的影响
dy = np.cos(vec_el)*np.sin(vec_az)  
dz = np.sin(vec_el)
#np.cos(vec_el）为单位光线在地平面上的投影长度

b = 225*(dx*uni_x + dy*uni_y + dz*uni_z) #梯度与光源相互作用，梯度转化为灰度
b = b.clip(0,255)  #防止数据越界，将生成的灰度值裁剪至0-225之间

im = Image.fromarray(b.astype('unit8'))  #重构图像
im.save('C:\\Users\\Public\\Pictures\\Saved Pictures\\structureHD.jpg') 

》》几个基本概念

图像深度值：

图像深度是指存储每个像素所用的位数，也用于量度图像的色彩分辨率。

图像梯度：

**梯度**的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。

**图像梯度**可以把图像看成**二维离散函数**，图像梯度其实就是这个二维离散函数的求导：

图像梯度: G(x,y) = dx(i,j) + dy(i,j);

dx(i,j) = I(i+1,j) - I(i,j); dy(i,j) = I(i,j+1) - I(i,j);

其中，I是图像像素的值(如：RGB值)，(i,j)为像素的坐标。 图像梯度一般也可以用中值差分： dx(i,j) = [I(i+1,j) - I(i-1,j)]/2; dy(i,j) = [I(i,j+1) - I(i,j-1)]/2;

图像边缘一般都是通过对图像进行梯度运算来实现的。

灰度：

灰度使用黑色调表示物体,即用黑色为基准色，不同的饱和度的黑色来显示图像。 每个灰度对象都具有从 0%（白色）到100%（黑色）的亮度值。

》》为什么归一化

基本上归一化思想是利用图像的不变矩寻找一组参数使其能够消除其他变换函数对图像变换的影响。也就是转换成唯一的标准形式以抵抗仿射变换

图像归一化使得图像可以抵抗几何变换的攻击，它能够找出图像中的那些不变量，从而得知这些图像原本就是一样的或者一个系列的

主要要通过归一化减小图片由于光线不均匀造成的干扰。

》》光源模型

   

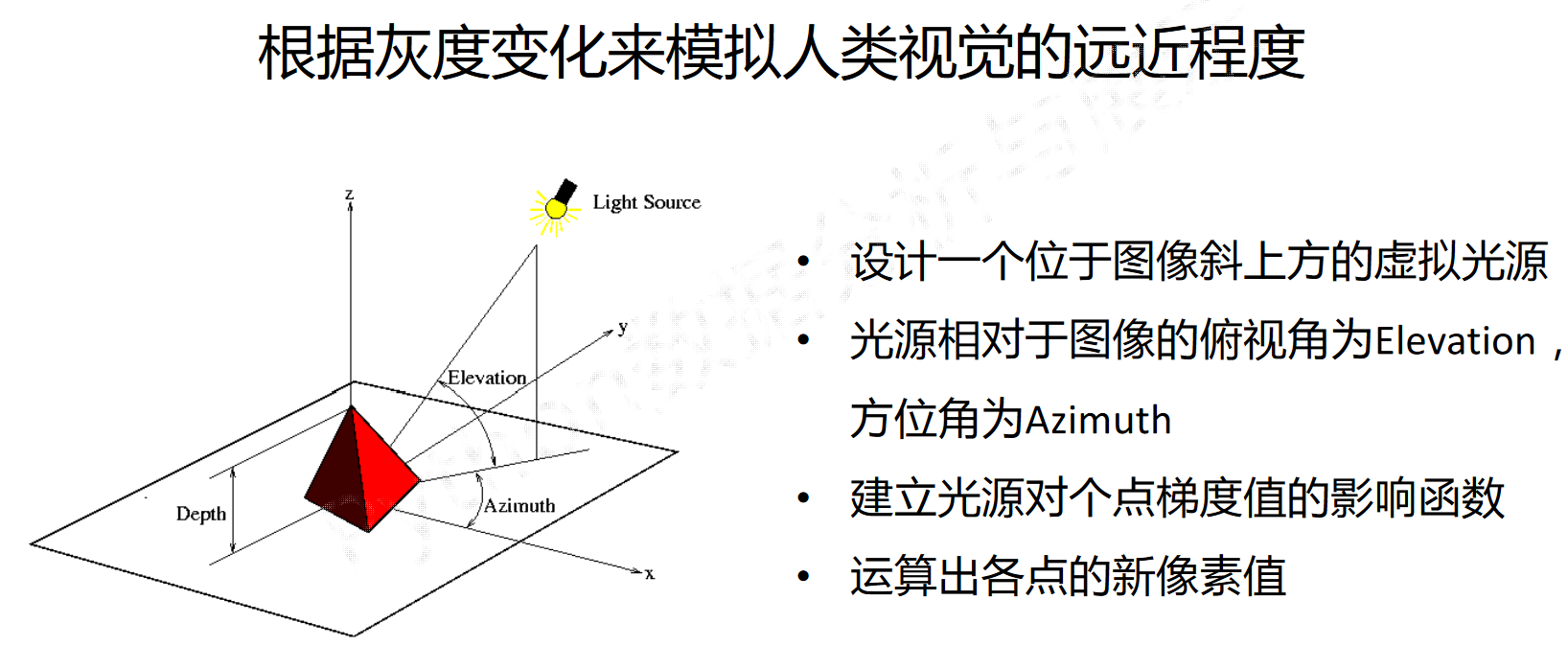
 ###注：文章笔记来自中国大学MOOC北京理工大学嵩天老师数据与分析课程