组合数学

排列与组合

定义

排列数：\(A_n^m=n\times(n-1)\times\dots\times(n-m+1)=\frac{n!}{(n-m)!}\) （从 \(n\) 个数里选 \(m\) 个数，不考虑选的数实际意义上相同的方案数）

全排列数：\(A_n^n\)

组合数：\(C_n^m=\frac{A_n^m}{A_n^n}\) （意思就是排列数的方案排序之后有可能是重复的，所以除以选出的 \(n\) 个数的全排列数）

圆排列数：\(Q_n^r=\frac{A_n^r}{r}\)（因为我们发现算完排列数可以转一圈，那也就重复了 \(r\) 次）

常用方法

1. 捆绑法：将必定相邻的物品当作一个整体先计算，之后再考虑整体方案数（用来处理某些物品必定相邻的问题）
2. 插空法：先计算其他没有要求的物品的方案数，再计算将有要求的数插进去的方案数（用来处理某些物品必定两两不相邻的问题）
3. 隔板法：就是在间隔之中选择一些来确定板子，从而达到分组的目的（用来处理无穷多重集的组合计数，即不定方程的根个数问题）
4. 对立法：其实就是正难则反（考虑事件的对立，用来处理含有“至少”这样含义的问题）

扩展

允许重复的组合

定理：在 \(n\) 个不同的元素中取 \(r\) 个进行组合，若允许重复，则组合数为 \(C(n+r−1,r)\) 。

证明：

设一个合法组合是 \(a_1,a_2,\dots,a_r\)，那么 \(1\le a_1\le\dots\le a_n\le n\)。

我们考虑这样一件事情：不允许重复的组合就是 \(1\le a_1< \dots< a_n\) ，那么考虑将此时的关系构造成这样：就是使 \(a_2+1,a_3+2,\dots,a_r+(r-1)\) 。

所以此时 \(1\le a_1<a_2+1<a_3+2<\dots<a_r+r-1\le n+r-1\) 。转化到这里就非常简单了，方案数就是 \(C(n+r-1,r)\) 。

等价问题：

1. 求方程 \(x_1+x_2+⋯+x_n=m\) 的非负整数解的个数，其中 \(n\) 和 \(m\) 都是整数，\(n≥1\)
2. \((x+\dots+z)^k\) 有多少项？

不相邻组合

定理：从 \(1\sim n\) 这 \(n\) 个自然数中选 \(k\) 个，这 \(k\) 个数中任何两个数都不相邻的组合有 \(C(n-k+1,k)\) 种。

证明：其实和允许重复的组合数一个方法证

经典问题

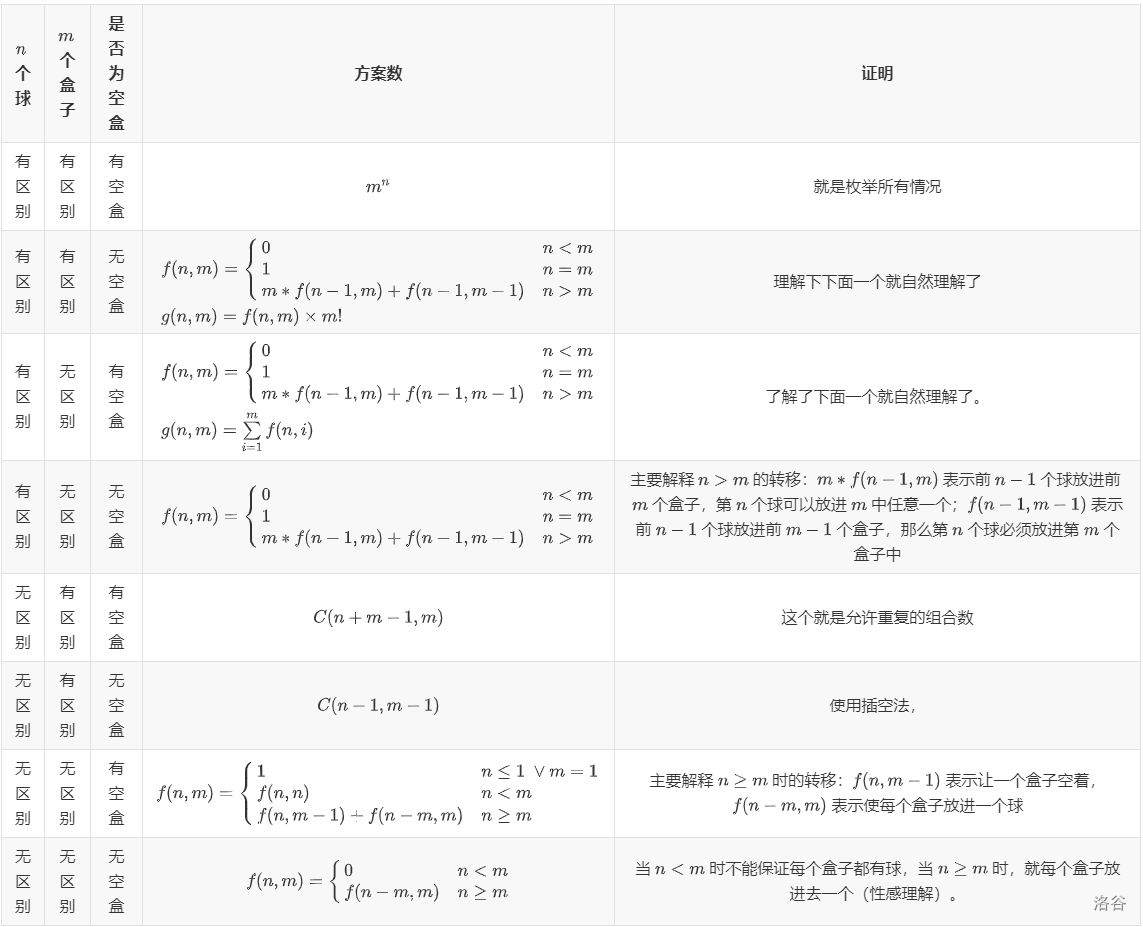
性质

对称性：\(C(n,m)=C(n-m,m)\)

递推式：\(C(n,m)=\frac{n}{m}C(n-1,m-1)\)

杨辉三角：\(C(n,m)=C(n-1,m)+C(n-1,m-1)\)（如果 \(n,m\) 较小，我们通常会考虑使用杨辉三角的递推式来预处理）

二项式定理

定理：\((a+b)^n=\sum\limits_{i=0}^n {n\choose k}a^{n-i}b^i\)

证明：

使用归纳法证明。

范德蒙恒等式

定理：\(\sum\limits_{i=0}^m {n\choose i}{m\choose k-i}={n+m\choose k}\)

证明：采用组合意义证明，考虑有两个班级，人数分别为 \(n,m\)，要选 \(k\) 个人就能理解了。

Lucas 定理

对于质数 \(p\)，有，

\[{n\choose m}\bmod p={\lfloor\frac{n}{p}\rfloor\choose\lfloor\frac{m}{p}\rfloor}*{n\bmod p \choose m\bmod p} \bmod p \]

证明：

Lucas 定理能够在 \(O(f(p)+g(n)\log n)\) 的时间复杂度下（\(f(p)\) 表示预处理组合数的复杂度，\(g(n)\) 表示单次求组合数的复杂度），求出一个组合数 \(C(n,m)\)。

其实我们可以使用乘法逆元 \(O(\log p)\) 求组合数：预处理一下阶乘即可

生成函数

定义

生成函数，也叫母函数。

常用的母函数有两个：

\(G(x)=\sum\limits_{i=0}^{+\infty} a_n x^n\) 和 \(G(x)=\sum\limits_{i=0}^{+\infty}a_n \frac{x^n}{n!}\)

形式幂级数形式：例如 \(G(x)=a_0+a_1x+\dots+a_nx^n+\dots\)

性质幂级数的封闭形式：例如 \(G(x)=(1+x)^n\)

性质

如果序列 \({a_n}\) 有通项公式，那么它的普通生成函数的系数就是通项公式。

扩展

母函数定理

设从 \(n\) 元集合 \(S={a_0,a_1,a_2,\dots,a_n}\) 中取 \(k\) 个元素的组合是 \(b_k\)，若限定元素 \(a_i\) 出现次数的集合为 \(M_i(1≤i≤n)\)，则该组合数序列的母函数为

\[\prod_{i=0}^n(\sum_{m\in M_i} x^m) \]

常见序列的普通母函数

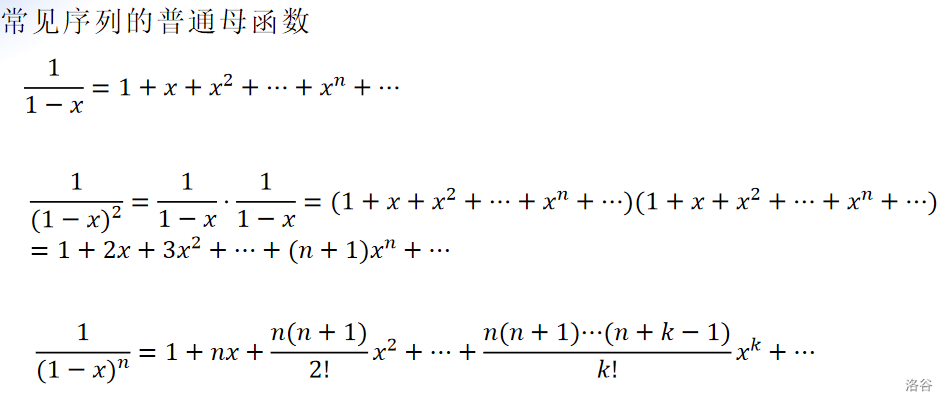
Fabonacci 数列

定义：\(f_0=0,f_1=1,f_i=f_{i-1}+f_{i-2}\) 。

之后带入原来的式子使用 \(\frac{1}{1-ax}=\sum\limits_{i=0} a^ix^i\) 得到 \(f_i\) 的通项公式：

\[f_x=\frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^n-(\frac{1-\sqrt{5}}{2})^n] \]

分拆数

定义

分拆：将自然数 \(n\) 写成递降正整数和的表示。

分拆数：\(p_n\) ，自然数 \(n\) 的分拆情况数（这个可以通过阈值分治，达到 \(O(n\sqrt{n})\) ，题目）

\(k\) 部分拆数：将 \(n\) 分成恰有 \(k\) 个部分的分拆，称为 \(k\) 部分拆数，记作 \(p(n,k)\)。

互异分拆数：\(pd_n\) 。自然数 \(n\) 的各部分互不相同的分拆方法数。

奇分拆数：\(po_n\)。自然数 \(n\) 的各部分都是奇数的分拆方法数。

递推式

\(p(n,k)\)：\(p(n,k)=p(n-1,k-1)+p(n-k,k)\)

\(pd(n,k)\)：\(pd(n,k)=pd(n-k,k-1)+pd(n-k,k)\)

\(po(n,k)\)：\(po(n,k)=po(n-k,k-1)+po(n-k,k)\)

容斥原理

定理

\[|\bigcup_{i=1}^{n}S_i|=\sum_i|S_i|-\sum_{i<j}|S_i\cap S_j|+\sum_{i<j<k}|S_i\cap S_j\cap S_k|-\dots+(-1)^{k-1}|\bigcap\limits_{i=1}^n S_i| \]

证明就是抽象成韦恩图的形式了。

一些定义

补集：\(\large|\overline{A}|=|U|-|A|\Rightarrow \bigcap\limits_{i=1}^n|S_i|=|U|-|\bigcup\limits_{i=1}^n \overline{S_i}|\)（\(|U|\)：表示全集）。

扩展

不定方程非整数解计数

\[\begin{cases} x_1+x_2+\dots+x_n=m \\ x_i\le b_i \\ m,b_i\in N & i=1,2\dots,n \end{cases} \]

如果没有这个 \(x_i\le b_i\) 的限制，那么我们可以发现，这就是一个球盒问题（将 \(m\) 个无区别的球放进 \(n\) 个有区别的盒子，盒子允许为空），方案数为 \({n+m-1\choose m}\)，虽然这只是一个弱化问题，但是这可以看作为一个解决该问题的全集 \(|U|\)，设 \(S_i\) 为 \(x_i\le b_i\) 满足情况的方案数，答案也就是 \(|\bigcap S_i|=|U|-|\bigcup \overline{S_i}|\)，现在目标是求 \(\bigcup \overline{S_i}\) 。

错位排列

\(D_n=(n-1)(D_{n-1}-D_{n-2})\)

证明：其实是分类讨论，假设将 \(n\) 放在 \(k(k\ne n)\)，如果 \(k\) 放在 \(n\) 处是 \(D(n-2)\)，如果 \(k\) 没有放在 \(n\) 处，等等，\(k\) 没有放在 \(n\) 处，这不是可以当作 \(D(n-1)\) 吗？由于 \(k\) 有 \(n-1\) 中取值，所以 \(D_n=(n-1)(D_{n-1}+D_{n-2})\) 。

经过不断的递推得到：\(D_n=nD_n+(-1)^n\)

通项公式

容斥原理推导欧拉函数

\(\varphi(n)\)：表示 \([1,n]\) 内与 \(n\) 互质数的个数。

通项公式：\(\varphi(n)=n\prod (\frac{p_i-1}{p_i})\) 。

证明：

首先，将 \(n\) 唯一分解 \(n=\prod\limits_{i=1}^m p_i^{k_i}\) .

之后，考虑使用容斥，\(S_i\) 表示和 \(n\) 有 \(i\) 个相同质因子。

那么，

\[\varphi(n)=n-\sum\limits_{i}\frac{n}{p_i}+\sum\limits_{i<j}\frac{n}{p_ip_j}-\dots+(-1)^k\frac{n}{p_1p_2\dots p_n} \\ =n{\Big(}1-\sum\limits_{i}\frac{1}{p_i}+\sum\limits_{i<j}\frac{1}{p_ip_j}-\dots+(-1)^k\frac{1}{p_1p_2\dots p_n}\Big) \\ =n\prod (\frac{p_i-1}{p_i}) \]

再给出最后一步的证明：

使用数学归纳法。

那么当 \(\Large\varphi(\frac{n}{p_m^{k_m}})=\frac{n}{p_m^{k_m}}\prod\limits^{m-1} (\frac{p_i-1}{p_i})\) 成立，

\[\varphi(n)=n{\Big(}1-\sum\limits_{i}\frac{1}{p_i}+\sum\limits_{i<j}\frac{1}{p_ip_j}-\dots+(-1)^k\frac{1}{p_1p_2\dots p_m}\Big) \\ 提出\frac{1}{p_m}得，\varphi(n)=n\prod\limits^{m-1} (\frac{p_i-1}{p_i})- n\Big(\frac{1}{p_m}(1-\sum\limits_{i\ne m}\frac{1}{p_i}+\sum\limits_{i<j,j\ne m}\frac{1}{p_ip_j}-\dots+(-1)^{k-1}\frac{1}{p_1p_2\dots p_{k-1} p_{k+1}\dots p_m})\Big) \\ \varphi(n)=n\prod\limits^{m-1} (\frac{p_i-1}{p_i})-n(\frac{1}{p_m}\Big(\prod\limits^{m-1} (\frac{p_i-1}{p_i})\Big) \\ \varphi(n)=n\prod (\frac{p_i-1}{p_i}) \]

广义容斥原理与狭义容斥原理

定义

\[\large \alpha(k)=\sum\limits_{i_1=1}^k\sum_{i_2=i_1+1}^k\dots\sum_{i_k=k}^k \Big| S_{i_1} \bigcap S_{i_2}\bigcap\dots\bigcap S_{i_k} \Big| \\ \large\beta(k) 为恰好有 k 个性质的元素个数 \]

广义容斥原理

\[\large\beta(k)=\sum\limits_{i=0}^{n-k} (-1)^i{k+i\choose k} \alpha(k+i) \]

这里的证明是考虑组合意义性感证明：

在这里考虑 \(\alpha(k)\) ：计数了具有 \(i+k\) 种性质的元素 \(i+k\choose k\) 次（其中 \(0\le i\le n-k\)），这是因为一个元素有 \(i+k\) 种性质，在统计至少有 \(k\) 种性质的元素时，这个元素的每 \(k\) 种性质就会使其产生 \(1\) 的贡献，而这个「每 \(k\) 种性质」一共会有 \(i+k\choose k\) 种。

狭义容斥原理

就是 \(\beta(0)\)！

莫比乌斯反演