图
1.学习总结
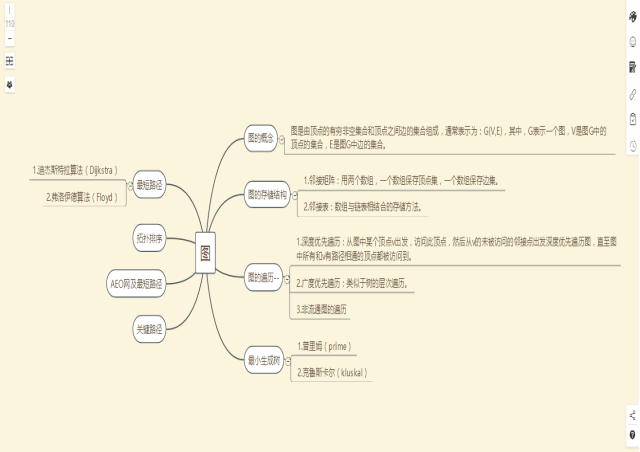
1.1图的思维导图
1.2 图结构学习体会
图的遍历有两种遍历方式:深度优先遍历和广度优先遍历
图的遍历:图的遍历有深度优先搜索和广度优先搜索,二者效率是一样的,时间复杂度为O(n+e)。
深度优先搜索
从图中某一顶点出发,访问后标记visit[i]为1,然后依次搜索第i个结点的领接点j,再依次搜索j结点的每个领接点,直到所有结点都被遍历搜索就是遍历整个图,把所有顶点遍历完,这就需要先定义一个数组,用来表示该顶点是否访问过。如果没访问过,就进行搜索,可以通过打印顶点名字表示搜索了,搜索后还要把该顶点表示为搜索过了。
广度优先搜索
这种搜索方式就和树的逐层遍历一样,先搜索A指向的所有顶点,然后搜索A指向的第一个顶点所指向的所有顶点,直到遍历完图,如果还有未搜索的,就再搜索它,和深度优先搜索的不同之处仅仅在于顶点的访问顺序不同。
3.深度优先遍历和广度优先遍历区别在于广度优先搜索与深度优先搜索的时间复杂度相同,只是遍历顺序不同。
Prim和Kruscal算法
Kruscal算法:
1.问题描述:设G=(V,E)是无向连通带权图,如果G的一个子图G’是一棵包含G的所有顶点的树,则称G’为G的生成树。生成树的各边权的总和称为该生成树的耗费,求在G的所有生成树中耗费最小的最小生成树。
2.算法思想:
(1)将代价树中权值非0的所有的边进行小顶堆排序,依次存入到road[]数组中,然后将road[]进行倒置,注意在进行排序时,按照road[i]的权值进行排序,然后记录这条边的起始顶点也要相对应。
(2)从最小边开始扫描各边,并检测当前所选边的加入是否会构成回路,如果不会构成回路,则将该边并入到最小生成树中。
(3)不断重复步骤2,直到所有的边都检测完为止。
其中判断当前检测边的加入是否会使原来生成树构成回路的算法思想是:
(1)采用树的双亲存储结构,即数组v[i]的值表示编号为i的顶点的父结点编号。并将数组v[]初始化为v[i]=i;
(2)若当前要并入的边起点为a,终点为b,需要判断起点a是否被修改过,即a!=v[a],若已被修改过,就要修改终点v[b]的值,使v[b]=a,即结点b的父结点为a。
(3)若当前检测的边结点起点为a,终点为b,则判断该边是否能被加入的方法是:分别访问a,b的根结点(a,b的父结点有可能还有父结点),若a,b的根结点相同,则不可以并入,否则可以将该边并入。
Prim算法:
此算法可以称为“加点法”,每次迭代选择代价最小的边对应的点,加入到最小生成树中。算法从某一个顶点s开始,逐渐长大覆盖整个连通网的所有顶点。
- 图的所有顶点集合为V;初始令集合u={s},v=V−u;
- 在两个集合u,v能够组成的边中,选择一条代价最小的边(u0,v0),加入到最小生成树中,并把v0并入到集合u中。
- 重复上述步骤,直到最小生成树有n-1条边或者n个顶点为止。
由于不断向集合u中加点,所以最小代价边必须同步更新;需要建立一个辅助数组closedge,用来维护集合v中每个顶点与集合u中最小代价边信息
,Dijkstra算法:
1.算法描述
1)算法思想:设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
2)算法步骤:
a.初始时,S只包含源点,即S={v},v的距离为0。U包含除v外的其他顶点,即:U={其余顶点},若v与U中顶点u有边,则<u,v>正常有权值,若u不是v的出边邻接点,则<u,v>权值为∞。
b.从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
c.以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
d.重复步骤b和c直到所有顶点都包含在S中
拓扑排序算法:
1.定义:是将一个有向无环图G的所有的顶点排成一个线性序列,使得有向图中的任意的顶点u 和 v 构成的弧<u, v>属于该图的边集,并且使得 u 始终是出现在 v 的前面。通常这样的序列称为是拓扑序列。
2.PTA实验作业(4分)
7-1 图着色问题
图着色问题是一个著名的NP完全问题。给定无向图G=(V,E),问可否用K种颜色为V中的每一个顶点分配一种颜色,使得不会有两个相邻顶点具有同一种颜色?
但本题并不是要你解决这个着色问题,而是对给定的一种颜色分配,请你判断这是否是图着色问题的一个解。
输入格式:输入在第一行给出3个整数V(0<V≤500)、E(≥0)和K(0<K≤V),分别是无向图的顶点数、边数、以及颜色数。顶点和颜色都从1到V编号。随后E行,每行给出一条边的两个端点的编号。在图的信息给出之后,给出了一个正整数N(≤20),是待检查的颜色分配方案的个数。随后N行,每行顺次给出V个顶点的颜色(第i个数字表示第i个顶点的颜色),数字间以空格分隔。题目保证给定的无向图是合法的(即不存在自回路和重边)。
输出格式:
对每种颜色分配方案,如果是图着色问题的一个解则输出Yes,否则输出No,每句占一行。
2.2 设计思路
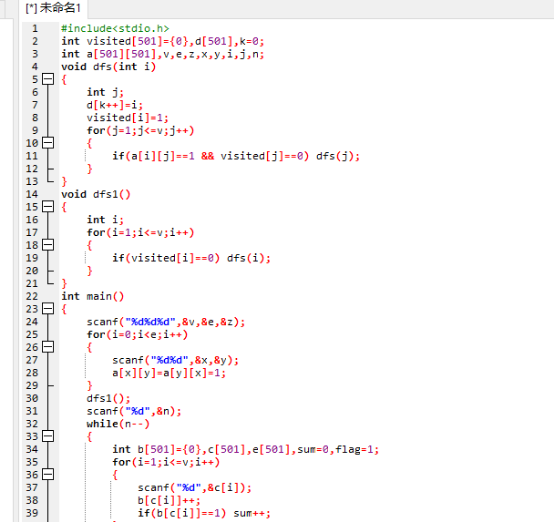
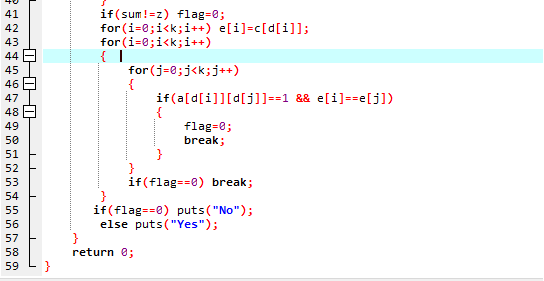
直接用图的遍历,遍历的时候判断是否颜色相等即可。
注意需要不同颜色的个数需要等于k。
2.3 代码截图
2.4 PTA提交列表说明

7-4 公路村村通
现有村落间道路的统计数据表中,列出了有可能建设成标准公路的若干条道路的成本,求使每个村落都有公路连通所需要的最低成本。
输入数据包括城镇数目正整数N(≤1000)和候选道路数目M(≤3N);随后的M行对应M条道路,每行给出3个正整数,分别是该条道路直接连通的两个城镇的编号以及该道路改建的预算成本。为简单起见,城镇从1到N编号。
输出格式:
输出村村通需要的最低成本。如果输入数据不足以保证畅通,则输出−1,表示需要建设更多公路。
直接用图的遍历,遍历的时候判断是否颜色相等即可。
注意需要不同颜色的个数需要等于k。
2.2 设计思路
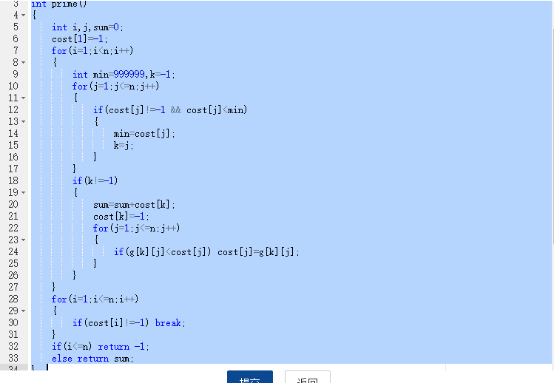
即运用普里姆算法求最小生成树
2.3 代码截图
2.4 PTA提交列表说明
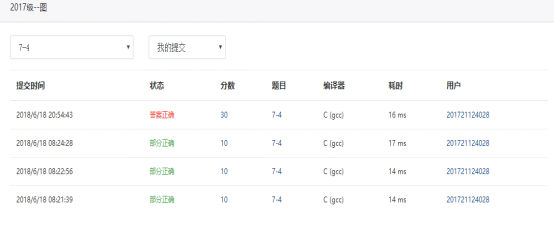
7-2 排座位
布置宴席最微妙的事情,就是给前来参宴的各位宾客安排座位。无论如何,总不能把两个死对头排到同一张宴会桌旁!这个艰巨任务现在就交给你,对任何一对客人,请编写程序告诉主人他们是否能被安排同席。
输入格式:
输入第一行给出3个正整数:N(≤100),即前来参宴的宾客总人数,则这些人从1到N编号;M为已知两两宾客之间的关系数;K为查询的条数。随后M行,每行给出一对宾客之间的关系,格式为:宾客1 宾客2 关系,其中关系为1表示是朋友,-1表示是死对头。注意两个人不可能既是朋友又是敌人。最后K行,每行给出一对需要查询的宾客编号。
这里假设朋友的朋友也是朋友。但敌人的敌人并不一定就是朋友,朋友的敌人也不一定是敌人。只有单纯直接的敌对关系才是绝对不能同席的。
输出格式:
对每个查询输出一行结果:如果两位宾客之间是朋友,且没有敌对关系,则输出No problem;如果他们之间并不是朋友,但也不敌对,则输出OK;如果他们之间有敌对,然而也有共同的朋友,则输出OK but...;如果他们之间只有敌对关系,则输出No way。
2.2 设计思路
需要考虑的情况:
如:A和B不认识,但是A和C是好朋友,B和D是好朋友,C和D是好朋友,那么,根据朋友的朋友是朋友的假设可得出,A和B是好朋友。
2.3 代码截图

2.4 PTA提交列表说明。
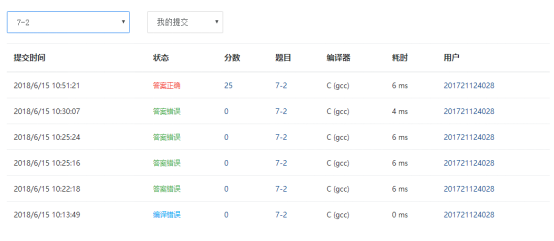
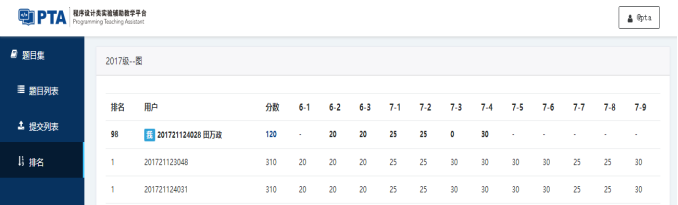
3.截图本周题目集的PTA最后排名
- 阅读代码
這是一个有关抢红包的代码:没有人没抢过红包吧…… 这里给出N个人之间互相发红包、抢红包的记录,请你统计一下他们抢红包的收获。
- #include<iostream>
- #include<algorithm>
- using namespace std;
- struct money
- {
- int id,value,cnt;
- }e[10001];
- int cmp(money a,money b)
- {
- if(a.value!=b.value) return a.value>b.value;
- else return a.cnt>b.cnt;
- }
- int main()
- {
- int n,m,x,y,i;
- cin>>n;
- for(i=0;i<n;i++)
- {
- e[i].id=i+1;
- cin>>m;
- while(m--)
- {
- cin>>x>>y;
- e[i].value=e[i].value-y;
- e[x-1].value=e[x-1].value+y;
- e[x-1].cnt++;
- }
- }
- stable_sort(e,e+n,cmp);
- for(i=0;i<n;i++)
- printf("%d %.2f\n",e[i].id,(double)(e[i].value/100.0));
- return 0;
- }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号