图像细化算法介绍与实现(Introduction and implementation of image thinning algorithm)
1. 图像细化基础理论
对图像细化的过程实际上是求图像骨架的过程。图像骨架是二维二值目标的重要拓扑描述,它指的是图像中央的骨骼部分,是描述像几何及拓扑性质的重要特征之一。例如一个长方形的骨架是其长方向上的中轴线,正方形的骨架是它的中心点,圆的骨架是它的圆心,直线的骨架是它自身,孤立点的骨架也是它自身。细化的目的就是在将图像的骨架提取出来的同时保持图像细小部分的连通性。对图像进行细化处理有助于突出形状特点和减少冗余信息量。
在细化一幅图像X的过程中应满足两个条件:
(1)在细化的过程中,X应该有规律地缩小;
(2)在X逐步缩小的过程中,应当使X的连通性质保持不变。
下面通过不同中心点的连接方式举例子来说明如何判断细化处理过程中是否满足以上两个条件。

上图中,每幅小图的中心点即要判断的是否满足条件的像素点,如满足条件则删除。
- 图(1)不能删,因为它是个内部点,要求的是骨架,如果连内部点也删了,骨架也会被掏空的;
- 图(2)不能删,和图(1)是同样的道理;
- 图(3)可以删,这样的点不是骨架;
- 图(4)不能删,因为删掉后,原来相连的部分也断开了;
- 图(5)可以删,这样的点不是骨架;
- 图(6)不能删,因为它是直线的端点,如果这样的点删了,那么最后整个直线也被删了。
2. Zhang-Suen细化算法。
Zhang-Suen算法由T.Y. Zhang和C.Y. Suen于1984年提出,是二值图像骨架提取的经典算法,广泛应用于OCR字符识别、指纹分析、医学图像处理(如血管提取)等领域。该算法通过迭代删除图像边界像素,最终得到单像素宽度的骨架结构,同时保持原始图像的拓扑特征。
Zhang-Suen细化算法相关说明定义:
(1)采用8邻域模型,定义中心像素p1的邻域位置,邻域图如图所示:

(2)在判断某个前景像素是否可以删除时,我们需计算以下两个值:
- N(p1) 即 p1 的 8 个邻域中前景(值为 1)的个数;
- S(p1) 即顺序遍历 p2, p3, …, p9, p2(构成闭环)时背景(0)到前景(1)的转变次数。举例说明:假设某像素的 8 邻域值序列为 (0, 1, 1, 0, 0, 0, 0, 0) ,则遍历序列 [0,1,1,0,0,0,0,0,0] 所得转变次数为 1。
Zhang-Suen细化算法具体流程:
Zhang-Suen通常是一个迭代算法,整个迭代过程分为两步:步骤一:循环所有前景像素点,对符合如下条件的像素点标记为删除:
(1)2 <= N(p1) <=6
(2)S(P1) = 1
(3)P2 * P4 * P6 = 0
(4)P4 * P6 * P8 = 0
步骤二:跟步骤1很类似,条件1、2完全一致,只是条件3、4稍微不同,满足如下条件的像素P1则标记为删除,条件如下:
(1)2 <= N(p1) <=6
(2)S(P1) = 1
(3)P2 * P4 * P8 = 0
(4)P2 * P6 * P8 = 0
循环上述两步骤,直到两步中都没有像素被标记为删除为止,输出的结果即为二值图像细化后的骨架。
3. 代码实现。
1 import cv2
2 import matplotlib.pyplot as plt
3
4
5 # 获取中心点附近的邻域值
6 def neighbours(x, y, image):
7 # Return 8-neighbours of image point P1(x,y), in a clockwise order
8 img = image
9 x_1, y_1, x1, y1 = x-1, y-1, x+1, y+1
10 return [img[x_1][y], img[x_1][y1], img[x][y1], img[x1][y1], # P2,P3,P4,P5
11 img[x1][y], img[x1][y_1], img[x][y_1], img[x_1][y_1]] # P6,P7,P8,P9
12
13
14 # 计算邻域值中从P2-P9-P2中0到1的突变次数
15 def transitions(data):
16 # "No. of 0,1 patterns (transitions from 0 to 1) in the ordered sequence"
17 n = data + data[0:1] # P2, P3, ... , P8, P9, P2
18 return sum((n1, n2) == (0, 1) for n1, n2 in zip(n, n[1:])) # (P2,P3), (P3,P4), ... , (P8,P9), (P9,P2)
19
20
21 # 实现Zhang_Suen细化算法
22 def Zhang_Suen_xihua(image_binary):
23
24 h, w = image_binary.shape[:2]
25 image_thinned = image_binary.copy()
26 flag1 = flag2 = 1
27
28 while flag1 or flag2:
29 flag1 = []
30 # numpy.full_like()函数的基本功能是创建一个与给定数组具有相同形状和数据类型的新数组,并用指定的值填充这个新数组
31 for i in range(1, h-1):
32 for j in range(1, w-1):
33 P2, P3, P4, P5, P6, P7, P8, P9 = data = neighbours(i, j, image_thinned)
34 if (image_thinned[i][j] == 1 and # Condition 0: Point P1 in the object regions
35 2 <= sum(data) <= 6 and # Condition 1: 2<= N(P1) <= 6
36 transitions(data) == 1 and # Condition 2: S(P1)=1
37 P2 * P4 * P6 == 0 and # Condition 3
38 P4 * P6 * P8 == 0): # Condition 4
39 flag1.append((i, j))
40
41 for i, j in flag1:
42 image_thinned[i][j] = 0
43
44 flag2 = []
45 # numpy.full_like()函数的基本功能是创建一个与给定数组具有相同形状和数据类型的新数组,并用指定的值填充这个新数组
46 for i in range(1, h-1):
47 for j in range(1, w-1):
48 P2, P3, P4, P5, P6, P7, P8, P9 = data = neighbours(i, j, image_thinned)
49 if (image_thinned[i][j] == 1 and # Condition 0: Point P1 in the object regions
50 2 <= sum(data) <= 6 and # Condition 1: 2<= N(P1) <= 6
51 transitions(data) == 1 and # Condition 2: S(P1)=1
52 P2 * P4 * P8 == 0 and # Condition 3
53 P2 * P6 * P8 == 0): # Condition 4
54 flag2.append((i, j))
55
56 for i, j in flag2:
57 image_thinned[i][j] = 0
58
59 # 画出结果图
60 plt.figure(), plt.title("original"), plt.imshow(image_binary, "gray")
61 plt.figure(), plt.title("thinned"), plt.imshow(image_thinned, "gray")
62 plt.show()
63
64
65 if __name__ == "__main__":
66 # 读取图片
67 image = cv2.imread("data/jisuan.jpg", 0)
68 _, binary = cv2.threshold(image, 127, 255, cv2.THRESH_BINARY) # 得到的图片背景是黑色,前景是白色
69 binary = binary/255 # 将前景从255改成1
70 Zhang_Suen_xihua(binary)
代码运行结果:

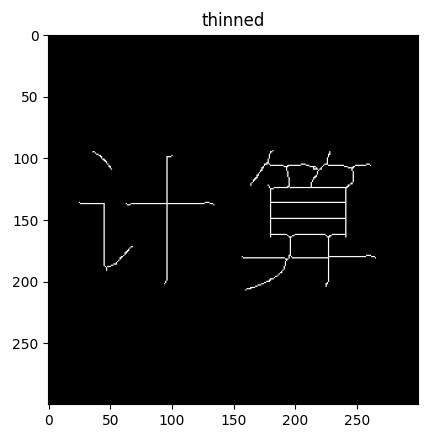
注意:在使用该算法时一定要保证前景目标为白色,背景为黑色,并且要求把前景目标的白色像素值设置为1.只有符合该条件时才可以直接使用以上算法,不然要修改一些参数。
这里提供原始图片方便复现代码:

参考资料:
《数字图像处理与深度学习技术应用》 杨淑莹 电子工业出版社 2024 ISBN:9787121483011
https://github.com/linbojin/Skeletonization-by-Zhang-Suen-Thinning-Algorithm
https://blog.csdn.net/u011447369/article/details/53375383


 浙公网安备 33010602011771号
浙公网安备 33010602011771号