三角函数

三角函数

1 三角函数

1.1 任意角

初中学的角度全都是从 0~360°，而高中最大的进步就是拓展了角度的范围，可以从负无穷到正无穷。

（1）任意角的定义：一条射线绕着端点在平面内旋转而成的图形，角的大小就是转过的角度，角的正负就是旋转的方向（逆时针为正）。

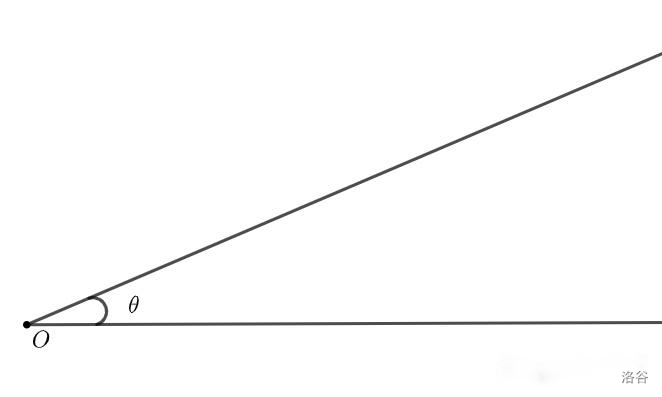
就像这个角是 \(\theta\) ，大家不要被迷惑，以为它看上去就是大约 20°，他也有可能是 380°（先逆时针转 360° 回到原位置，再逆时针转 20°），甚至有可能是 -340°（顺时针转一圈不到 20°），还有更多可能。

（2）任意角的正负：强调一下逆时针为正。

（3）任意角的象限：

其实就是把这条射线的初始位置放到 \(x\) 轴，并且把原点和射线的起点重合。因此每一个角都会落在某个象限或者某个坐标轴上。

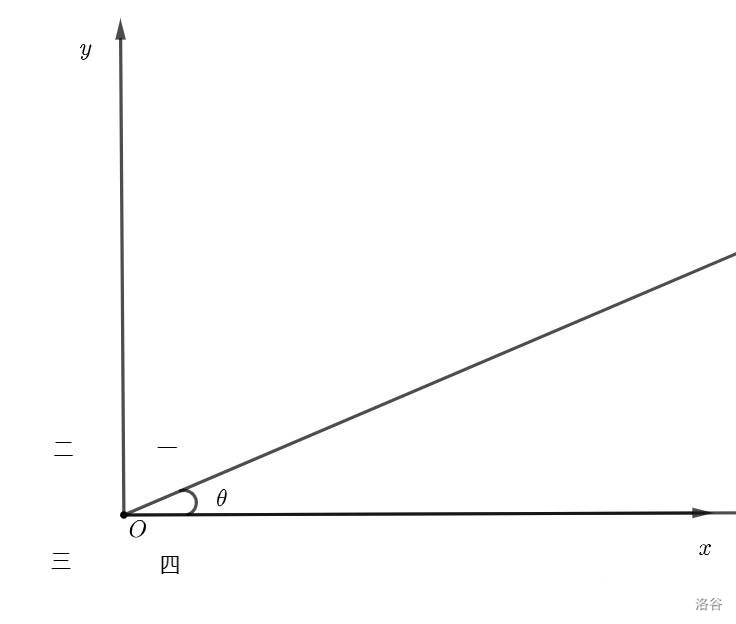
此时的角就落在第一象限

1.2 弧度制

弧度制的作用就是更方便地求弧长。除此之外它就打不过角度制了。

（1）定义：弧长和半径相等的圆心角就是 1 弧度的角。单位为 rad，读作弧度，这种用“弧度”来表示角度的方法叫做弧度制。

（2）弧长计算公式

\[l=\theta R\\ \]

能够更加方便地求出弧长，这就是弧度制最大的魅力。

（3）弧度制和角度制的转换：

\[2\pi=360° \Longrightarrow\pi=180° \Longrightarrow\frac{\pi}{2}=90° \\\Longrightarrow\frac{\pi}{4}=45°\Longrightarrow\frac{\pi}{3}=60°\Longrightarrow\frac{\pi}{6}=30° \]

1.3 任意角的三角函数

（1）定义：设 \(\theta\) 是一个任意角，它的终边和单位圆的交点为 \(P(a,b)\) ，如图：

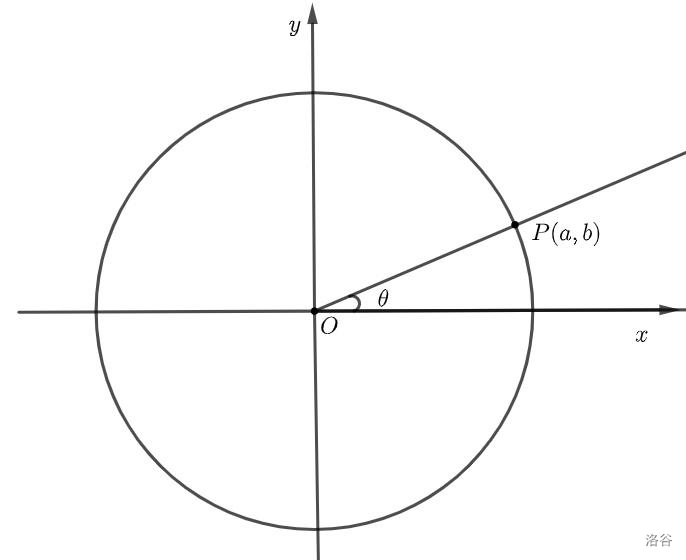
\[\sin{\theta}=b,\cos{\theta}=a,\tan{\theta}=\frac{b}{a}\\ \]

注：
①三个三角函数都有可能是负值，具体取决于 \(a\) 和 \(b\) 的正负。
②正弦和余弦的定义域是 \(R\) ，但是正切的定义域为 \(\{\theta|\theta\ne k\pi+\frac{\pi}{2},k\in Z\}\)

1.4 诱导公式

对于三角函数，根据它的定义，有下列诱导公式

\[\sin(\alpha+k\cdot 2\pi)=\sin\alpha,\cos(\alpha+k\cdot 2\pi)=\cos\alpha,\tan(\alpha+k\cdot 2\pi)=\tan\alpha\\[5pt] \sin{(-\alpha)}=-\sin{\alpha},\cos{(-\alpha)}=\cos{\alpha},\tan{(-\alpha)}=-\tan{\alpha}\\[5pt] \sin{(\pi\pm\alpha)}=\mp\sin{\alpha},\cos{(\pi\pm\alpha)}=-\cos{\alpha},\tan{(\pi\pm\alpha)}=\pm\tan{\alpha}\\[5pt] \sin{(\frac{\pi}{2}\pm\alpha)}=\cos{\alpha},\cos{(\frac{\pi}{2}\pm\alpha)}=\mp\sin{\alpha},\tan{(\frac{\pi}{2}\pm\alpha)}=\mp\cot{\alpha}\\[5pt] \]

通过上面的公式我们就可以把所有的角都化为一个锐角了，锐角处理起来还不是有手就行。至于推导的话主要遵循一个口诀：奇变偶不变，符号看象限。

怎么理解“奇变偶不变，符号看象限”?

诱导公式可概括为角 \(k\cdot\displaystyle\frac{\pi}{2}\pm\alpha(k\in\Z)\) 的各三角函数值的化简公式。奇与偶指角 \((k\cdot\displaystyle\frac{\pi}{2}\pm\alpha)\) 中 \(\displaystyle\frac{\pi}{2}\) 的倍数 \(k\) 的奇偶；变与不变指的是三角函数名，变是指正弦变余弦、余弦变正弦，不变是指三角函数名不变；符号看象限是指把角 \(\alpha\) 看成锐角时原函数值的符号.

1.5 三角函数的图像

我们可以画出三角函数的图像，例如

\(y=2\sin{(x+\displaystyle\frac{\pi}{3})}\) 的图像为

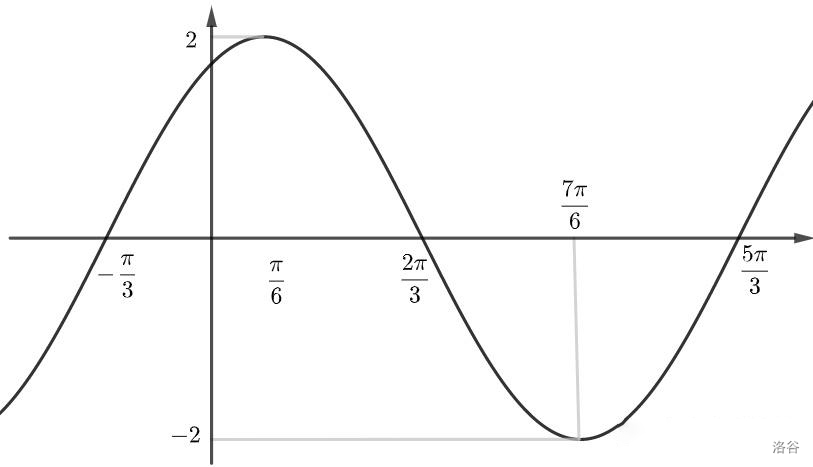
在数学中，这是典型的五点法作图。

更多具体的图像我们留到振动和波动章节再细说。

2 三角恒等变换

2.1 三角恒等变换的基本概念

三角恒等变换是数学的一类公式，用于三角等价变化。咳咳咳，最重要的其实还是在同学面前装13，接下去的内容两角和差公式以及辅助角公式需要牢牢掌握，和差化积、积化和差以及万能公式就可以记下来在同学面前装13了。

2.2 两角和差公式

\[\sin(\alpha\pm\beta)=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta, \cos(\alpha\pm\beta)=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta\\[5pt] \tan(\alpha\pm\beta)=\frac{\tan\alpha\pm\tan\beta}{1\mp\tan\alpha\tan\beta}\Rightarrow\tan\alpha\pm\tan\beta=\tan(\alpha\pm\beta)(1\mp\tan\alpha\tan\beta)\\[5pt] \]

这是最最最最重要的公式，一定要背下来。就像张无忌的九阳神功，没有九阳神功他也学不会乾坤大挪移。

2.3 辅助角公式

（1）作用

辅助角公式常用来求极值。

（2）辅助角公式

\[a\sin{\alpha}+b\cos{\alpha}=\sqrt{a^2+b^2}\sin(\alpha+\varphi)\\[5pt] \sin{\varphi}=\frac{b}{\sqrt{a^2+b^2}},\cos{\varphi}=\frac{a}{\sqrt{a^2+b^2}},\tan{\varphi}=\frac{b}{a}\\[5pt] \]

【例题】求函数 \(f(x)=(1+\sqrt3\tan{x})\cos{x}(x\in R)\) 的最大值。

【解析】

\[f(x)=\cos{x}+\sqrt3\sin{x}=2\sin{(x+\frac{\pi}{6})}\\ \therefore f_{max}=2 \]

2.4 二倍角公式

\[\sin{2\alpha}=2\sin\alpha\cos\alpha\Rightarrow 1\pm\sin2\alpha=\sin^2\alpha+\cos^2\alpha\pm2\sin\alpha\cos\alpha=(\sin\alpha\pm\cos\alpha)^2\\[5pt] \cos{2\alpha}=\cos^2{\alpha}-\sin^2{\alpha}=2\cos^2{\alpha}-1=1-2\sin^2{\alpha},\tan{2\alpha}=\frac{2\tan{\alpha}}{1-\tan^2{\alpha}}\\[5pt] \]

【例题】求函数 \(f(\alpha)=\displaystyle\frac{1}{2}\cos{2\alpha}+\cos{\alpha}(x\in[0,2\pi])\) 的最小值。

【解析】

\[f(\alpha)=\frac{1}{2}\cos{2\alpha}+\cos{\alpha}=\frac{1}{2}(2\cos^2{\alpha}-1)+\cos{\alpha}\\ =\cos^2{\alpha}+\cos{\alpha}-\frac{1}{2}=(\cos{\alpha}+\frac{1}{2})^2-\frac{3}{4}\\ \therefore f_{min}=-\frac{3}{4} \]

2.5 升幂、降幂公式

\[1+\cos\alpha=2\cos^2\frac{\alpha}{2},1-\cos\alpha=2\sin^2\frac{\alpha}{2}\\[5pt] \cos^2\alpha=\frac{1+\cos2\alpha}{2},\sin^2\alpha=\frac{1-\cos2\alpha}{2}\\[5pt] \]

2.6 半角公式

\[\sin\frac{\alpha}{2}=\pm\sqrt{\displaystyle\frac{1-\cos\alpha}{2}},\cos\frac{\alpha}{2}=\pm\sqrt{\displaystyle\frac{1+\cos\alpha}{2}}\\[5pt] \tan\frac{\alpha}{2}=\pm\sqrt{\displaystyle\frac{1-\cos\alpha}{1+\cos\alpha}}=\frac{\sin\alpha}{1+\cos\alpha}=\frac{1-\cos\alpha}{\sin\alpha}\\[5pt] \]

2.7 万能公式

\[\sin{\alpha}=\frac{2\tan{\displaystyle\frac{\alpha}{2}}}{1+\tan^2{\displaystyle\frac{\alpha}{2}}},\cos{\alpha}=\frac{1-\tan^2{\displaystyle\frac{\alpha}{2}}}{1+\tan^2{\displaystyle\frac{\alpha}{2}}},\tan{\alpha}=\frac{2\displaystyle\tan{\frac{\alpha}{2}}}{1-\tan^2{\displaystyle\frac{\alpha}{2}}}\\ \]

2.8 积化和差

\[\sin{\alpha}\cos{\beta}=\frac{1}{2}[\sin{(\alpha}+\beta)+\sin{(\alpha}-\beta)]\\[5pt] \cos{\alpha}\sin{\beta}=\frac{1}{2}[\sin{(\alpha}+\beta)-\sin{(\alpha}-\beta)]\\[5pt] \cos{\alpha}\cos{\beta}=\frac{1}{2}[cos{(\alpha}+\beta)+\cos{(\alpha}-\beta)]\\[5pt] \sin{\alpha}\sin{\beta}=-\frac{1}{2}[cos{(\alpha}+\beta)-\cos{(\alpha}-\beta)]\\[5pt] \]

证明：

emm证明的话其实和差化积和积化和差可以互证（把和差化积的 \(\alpha\) 换为 \(\alpha+\beta\) ， \(\beta\) 换为 \(\alpha-\beta\) 就得到了积化和差，其实用两角和差公式展开就行了）

\[\frac{1}{2}[\sin{(\alpha}+\beta)+\sin{(\alpha}-\beta)]\\ =\frac{1}{2}[\sin\alpha\cos\beta+\cos\alpha\sin\beta+\sin\alpha\cos\beta-\cos\alpha\sin\beta]\\ =\frac{1}{2}[2\sin\alpha\cos\beta]=\sin\alpha\cos\beta \]

后面的三个公式就不证明了，证明方法相同。需要知道的是，其实积化和差、和差化积公式都是从最基础的两角和差公式推演过来的，因此大家需要把握住两角和差公式。

【例题】若 \(\cos{(\alpha+\beta)}\cos{(\alpha-\beta)}=\displaystyle\frac{1}{3}\) ，求 \(\cos^2{\alpha}-\sin^2{\beta}\) 。

【解析】

根据积化和差公式的第三个公式

\[\cos{(\alpha+\beta)}\cos{(\alpha-\beta)}=\frac{1}{2}(\cos{2\alpha}+\cos{2\beta})\\ =\frac{1}{2}(2\cos^2{\alpha}-1+1-2\sin^2{\beta})=\cos^2{\alpha}-\sin^2{\beta}=\frac{1}{3} \]

2.9 和差化积公式

\[\sin{\alpha}+\sin{\beta}=2\sin{\frac{{\alpha}+\beta}{2}}\cos{\frac{{\alpha}-\beta}{2}}\\[5pt] \sin{\alpha}-\sin{\beta}=2\cos{\frac{{\alpha}+\beta}{2}}\sin{\frac{{\alpha}-\beta}{2}}\\[5pt] \cos{\alpha}+\cos{\beta}=2\cos{\frac{{\alpha}+\beta}{2}}\cos{\frac{{\alpha}-\beta}{2}}\\[5pt] \cos{\alpha}-\cos{\beta}=-2\sin{\frac{{\alpha}+\beta}{2}}\sin{\frac{{\alpha}-\beta}{2}}\\[5pt] \]

3 解三角形

三角形是大家见到的最基础的图形，那么它的三条边和三个角有什么关系呢？一般我们把三条边记为 \(a,b,c\) ，三条边的 对角记为 \(A,B,C\) ，这一小节我们将介绍三角形中两个基本定理：正弦定理和余弦定理。

3.1 正弦定理

3.1.1 内容

\[\frac{a}{\sin{A}}=\frac{b}{\sin{B}}=\frac{c}{\sin{C}}=2R\\ \]

其中 \(R\) 是三角形内接圆的半径。

3.1.2 证明

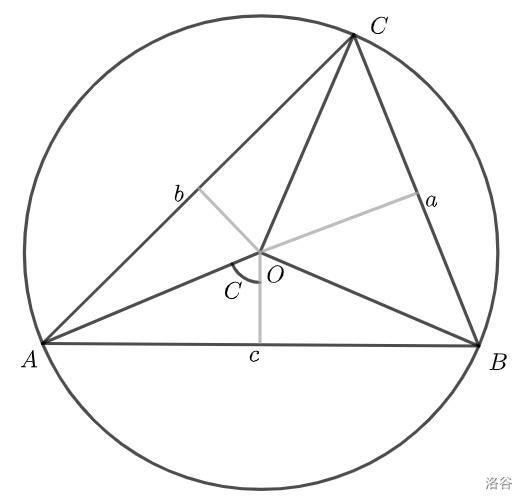
根据圆周角和圆心角的关系\(\angle{AOB}=2C\)，因此 \(\overline{AB}=c=2R\sin{C}\) ，所以我们就能得到 \(\frac{\displaystyle c}{\displaystyle\sin{C}}=2R\)，其他边的证明同理。

证毕。

3.2 余弦定理

3.2.1 内容

\[\begin{aligned} a^2&=b^2+c^2-2bc\cos{A}\\[5pt] b^2&=c^2+a^2-2ac\cos{B}\\[5pt] c^2&=a^2+b^2-2ab\cos{C}\\[5pt] \end{aligned} \]

还有一些推论

\[\begin{aligned} \cos a&=\frac{b^2+c^2-a^2}{2bc}\\[5pt] \cos b&=\frac{a^2+c^2-b^2}{2ac}\\[5pt] \cos c&=\frac{a^2+b^2-c^2}{2ab}\\[5pt] \end{aligned} \]

注：勾股定理其实只是余弦定理的特例，现在能够感受到余弦定理的厉害之处了吧。

3.2.2 证明

在 \(\triangle ABC\) 中由 \(\vec{CB}= \vec{AB}-\vec{AC}\) 可得

\[\begin{aligned} \vec{CB}\cdot\vec{CB}=&(\vec{AB}-\vec{AC})\cdot(\vec{AB}-\vec{AC})\\ =&\vec{AB}^2+\vec{AC}^2-2\vec{AB}\cdot\vec{AC}\\ =&b^2-c^2-2bc\cos A \end{aligned} \]

即 \(a^2=b^2-c^2-2bc\cos A\)，其他边的证明同理。

证毕。

3.3 一些应用

\[S\triangle ABC=\frac{1}{2}ab\sin C=\frac{1}{2}ac\sin B=\frac{1}{2}bc\sin A \]

还有些别的先待我先学习学习再补充。