学习笔记：莫队

莫队

莫队是由莫涛发明的一种适用于区间查询等问题的离线算法。基于分块思想，时间复杂度为 $O(n\sqrt{n})$。

一般地，如果在知道区间 $[l,r]$ 的答案的情况下可以在 $O(1)$ 或 $O(\log n)$ 内通过运算很方便地得到区间 $[l,r+1]$，$[l,r-1]$，$[l+1,r]$，$[l-1,r]$ 的答案时则可以考虑使用莫队算法。

通常情况下，如果转移的时间复杂度是 $O(1)$ 的话，则总的时间复杂度大概是 $O(n\sqrt{n})$；如果转移的时间复杂度是 $O(\log n)$ 的话，则总的时间复杂度大概是 $O(n\sqrt{n}\log n)$。

下面来看一道莫队的板子题：

SP3267 DQUERY - D-query

简要题意

给定一个长度为 $n$ 的序列，总共有 $q$ 个询问，对于每个询问区间 $[l,r]$，你需要求出区间 $[l,r]$ 中一共有多少不同的数字。

样例

样例输入 #1

5
1 1 2 1 3
3
1 5
2 4
3 5

样例输出 #1

3
2
3

解析

这道题也可以用树状数组做，但用莫队的话思维难度会比较低，相对比较好想。

之前说过，我们要把一个区间的答案转移到与之相邻的区间中去，具体怎么做呢？我们用一个数组 Cnt[] 来记录每个数出现的次数，cur 表示当前区间的答案。

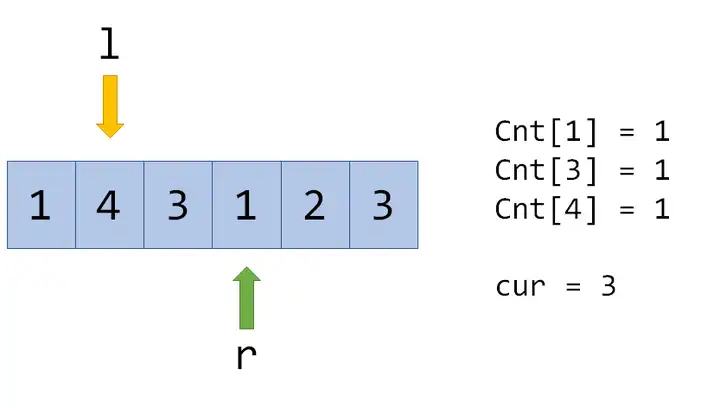
现在转移到紧邻的区间就很简单了，例如转移到 $[l,r+1]$：

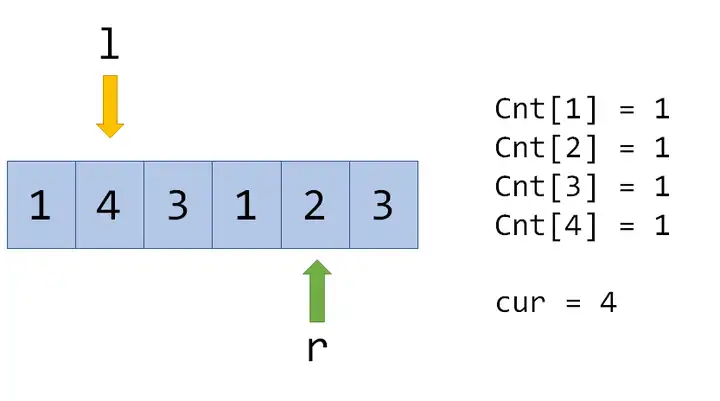
$Cnt[2]=0$，说明添加了一个没出现过的数，所以 $cur$ 变成 $4$，但如果在这里再次向右转移：

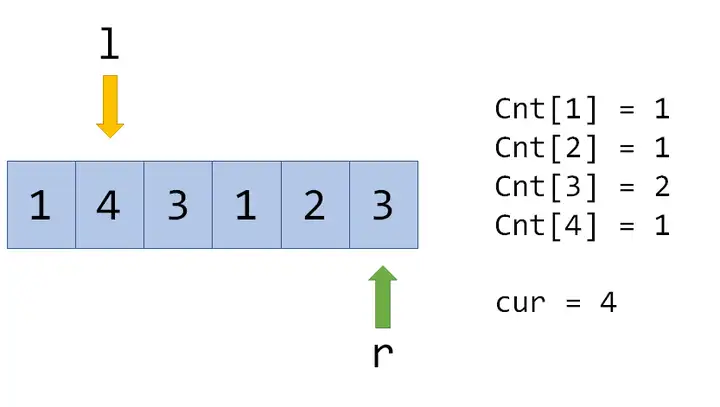
这时 $Cnt[3]$ 不为 $0$，所以虽然 $Cnt[3]$ 增加，但是 $cur$ 不再增长。

其他的转移都是类似的。容易发现，转移分为两种情况，往区间里添加数，或者往区间里删除数，所以可以写成两个函数：

void add(int node){
    if(cnt[arr[node]] == 0)cur++;
    cnt[arr[node]]++;
}
void del(int node){
    cnt[arr[node]]--;
    if(cnt[arr[node]] == 0)cur--;
}

那么从任意一个区间移动到另一个区间，只需写：

    while(l > q[i].left)add(--l);
    while(r < q[i].right)add(++r);
    while(l < q[i].left)del(l++);
    while(r > q[i].right)del(r--);

注意增加和减少的位置。删数是先删后移，添数是先移后添。初始化时，要先令 $l=1$，$r=0$。

现在我们可以从一个区间的答案转移到另一个区间了。但是，如果直接在线查询，很有可能在序列两头“左右横跳”，在部分情况下甚至还不如朴素的 $O(n^2)$ 算法。但是，我们可以把查询离线下来（记录下来），然后再对所有询问进行排序。

问题来了，怎么排序？我们很容易想到以 $l$ 为第一关键词，$r$ 为第二关键词排下序，但这样做效果并不是很好，显然还有更优的做法。莫涛大神给出的方法是分块，然后按照 bel[l] 为第一关键词，bel[r] 为第二关键词排序。 这样，每两次询问间l和r指针移动的距离可以被有效地降低，整个算法的时间复杂度可以降到 $O(n\sqrt{n})$！但在此之上，我们还可以进行常数优化：奇偶化排序。意为：如果 bel[l] 是奇数，则将 r 顺序排序，否则将 r 逆序排序。 这为什么有效？如果按照一般的排序方法，指针的动向可能是这样的：

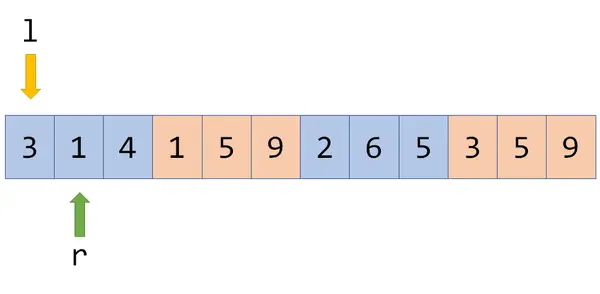
我们看到，每次 $l$ 跨过一个块时，$r$ 都必须往左移很长一截。

而奇偶化排序后，指针的动向会变为这样：

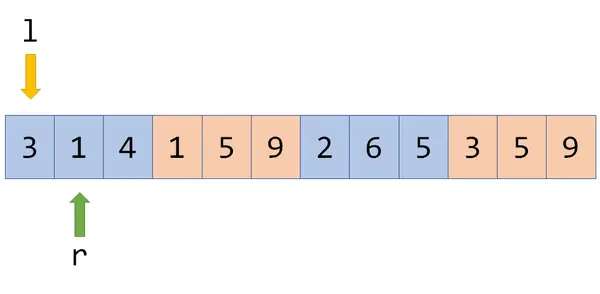
可以发现，如果 $l$ 在偶数块，$r$ 指针会在返回的“途中”就解决问题。

这就是普通莫队算法，给出上面那道例题的主要代码：

#include <bits/stdc++.h>
#define MAXN 30005
#define MAXA 1000005
#define MAXQ 200005
using namespace std;
int n, op, len, cur, l = 1, r = 0;
struct query{
    int left, right, id;
    bool operator<(const query &x)const{
        if(left / len != x.left / len)return left < x.left;
        if(left / len & 1)return right < x.right;
        return right > x.right;
    }
}q[MAXQ];
int ans[MAXQ], cnt[MAXA], arr[MAXN];
int read(){
    int t = 1, x = 0;char ch = getchar();
    while(!isdigit(ch)){if(ch == '-')t = -1;ch = getchar();}
    while(isdigit(ch)){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
    return x * t;
}
void write(int x){
    if(x < 0){putchar('-');x = -x;}
    if(x >= 10)write(x / 10);
    putchar(x % 10 + '0');
}
void add(int node){
    if(cnt[arr[node]] == 0)cur++;
    cnt[arr[node]]++;
}
void del(int node){
    cnt[arr[node]]--;
    if(cnt[arr[node]] == 0)cur--;
}
int main(){
    n = read();
    len = sqrt(n);
    for(int i = 1 ; i <= n ; i ++)arr[i] = read();
    op = read();
    for(int i = 1 ; i <= op ; i ++){q[i].left = read();q[i].right = read();q[i].id = i;}
    sort(q + 1, q + op + 1);
    for(int i = 1 ; i <= op ; i ++){
        while(l > q[i].left)add(--l);
        while(r < q[i].right)add(++r);
        while(l < q[i].left)del(l++);
        while(r > q[i].right)del(r--);
        ans[q[i].id] = cur;
    }
    for(int i = 1 ; i <= op ; i ++){write(ans[i]);putchar('\n');}
    return 0;
}

记住，只要询问可以离线（有些题目会要求强制在线，就不能用这个方法了）且可以在 $O(1)$ 或者 $O(\log n)$ 内实现转移，就可以用这个方法，而且很多时候只需要修改一下 add() 和 del() 函数即可。