学习笔记:最近公共祖先
最近公共祖先
引入
LCA,即最近公共祖先。通俗地讲,可以感性理解为:树上任意两点的最近公共祖先就是以这两个点为起点向树根走,两边最先相遇的点就是最近公共祖先。
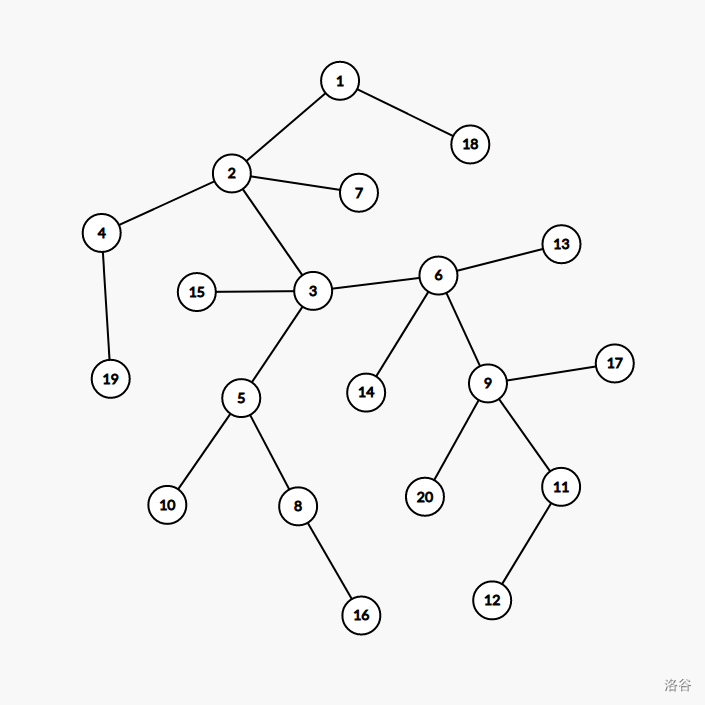
以上图为例,如果以节点 $1$ 作为树根的话,$10$ 和 $16$ 的最近公共祖先是 $5$,$12$ 和 $14$ 的最近公共祖先是 $6$。不理解的可以尝试在纸上模拟一下。
求法
至于求解的话,可以直接跟之前讲的那样直接一步一步往树根走,直到两边相互遇到。
然而,这种方法虽然简单直观,在一些数据规模较大的题目中就显得有点力不从心了。这个时候我们就需要考虑一些比较有意思的优化:
倍增求 LCA
既然一次走一步太慢,那就考虑一次走多步,很容易就能想到倍增。
所谓倍增,就是按 $2$ 的倍数来增大,也就是跳 $1$,$2$,$4$,$8$,$16$,$32$,…… 不过在这我们不是按从小到大跳,而是从大向小跳,即按 ……,$32$,$16$,$8$,$4$,$2$,$1$ 来跳,如果大的跳不过去,再把它调小。这是因为从小开始跳,可能会出现“悔棋”的现象。拿 $5$ 为例,从小向大跳,$5\ne 1+2+4$,所以我们还要回溯一步,然后才能得出 $5=1+4$;而从大向小跳,直接可以得出 $5=4+1$。这也可以拿二进制为例,$5_{(10)}=101_{(2)}$,从高位向低位填很简单,如果填了这位之后比原数大了,那我就不填,这个过程是很好操作的。
以上图为例,如果以节点 $1$ 作为树根的话,要求 $12$ 和 $16$ 的最近公共祖先,暴力跳的路径是这样的:$$ 12\Rightarrow 11\Rightarrow 9\Rightarrow 6\Rightarrow 3 \\ 16\Rightarrow 8\Rightarrow 5\Rightarrow 3 \\ $$ 如果采用倍增法的话,路径就会变成这样:$$ 12\Rightarrow 3 \\ 16\Rightarrow 5\Rightarrow 3 $$ 可以试着感性理解一下。
不难看出,倍增优化下的路径得到了优化。实际上,倍增优化的时间复杂度是 $O(n\log n)$,这个时间复杂度已经可以满足大部分需求了。
那么,倍增优化具体应该如何实现呢?
首先应当预处理一个倍增数组。
for(int i = 1 ; i <= n ; i ++)lg[i] = lg[i >> 1] + 1;在这里,$lg_i$ 表示 $log_2i + 1$ 的值。
对于每一个点,我们记录它的 $2^i$ 级祖先和深度。显然有:
- $fa_{i,j}$ 表示节点 $i$ 的 $2^j$ 级祖先。
- $dep_i$ 表示节点 $i$ 在树中的深度。
void dfs(int u, int fat){
fa[u][0] = fat;dep[u] = dep[fat] + 1;
for(int i = 1 ; i <= lg[dep[u]] ; i ++)fa[u][i] = fa[fa[u][i - 1]][i - 1];
for(int i = head[u] ; i != 0 ; i = e[i].nxt){
int v = e[i].to;if(v != fat)dfs(v, u);
}
}中间的转移意思是:节点 $u$ 的 $2^i$ 级祖先等于节点 $u$ 的 $2^{i-1}$ 级祖先的 $2^{i-1}$ 级祖先。
证明:显然有 $2^i=2^{i-1}+2^{i-1}$。
接下来就是倍增LCA了,我们先把两个点提到同一高度,再统一开始跳。但我们在跳的时候不能直接跳到它们的 LCA,因为这可能会误判,比如 $4$ 和 $6$,在跳的时候,我们可能会认为 $1$ 是它们的LCA,但 $1$ 只是它们的祖先,它们的 LCA 实际上是 $2$。所以我们要跳到它们 LCA 的下面一层,比如 $10$ 和 $20$,我们就分别跳到 $5$ 和 $6$,然后输出它们的父节点,这样就不会误判了。
int lca(int x, int y){
if(dep[x] < dep[y])swap(x, y);
while(dep[x] > dep[y])x = fa[x][lg[dep[x] - dep[y]] - 1];
if(x == y)return x;
for(int i = lg[dep[x]] - 1 ; i >= 0 ; i --){
while(fa[x][i] != fa[y][i])
x = fa[x][i],y = fa[y][i];
}return fa[x][0];
}附上完整代码。
#include <iostream>
#define MAXN 500005
using namespace std;
int n, m, s, x, y;
int fa[MAXN][25], lg[MAXN], dep[MAXN];
struct edge{int to, nxt;}e[MAXN << 1];
int head[MAXN], cnt = 1;
int read(){
int t = 1, x = 0;char ch = getchar();
while(!isdigit(ch)){if(ch == '-')t = -1;ch = getchar();}
while(isdigit(ch)){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * t;
}
void write(int x){
if(x < 0){putchar('-');x = -x;}
if(x >= 10)write(x / 10);
putchar(x % 10 ^ 48);
}
void add(int u, int v){
cnt++;e[cnt].to = v;e[cnt].nxt = head[u];head[u] = cnt;
cnt++;e[cnt].to = u;e[cnt].nxt = head[v];head[v] = cnt;
}
void dfs(int u, int fat){
fa[u][0] = fat;dep[u] = dep[fat] + 1;
for(int i = 1 ; i <= lg[dep[u]] ; i ++)fa[u][i] = fa[fa[u][i - 1]][i - 1];
for(int i = head[u] ; i != 0 ; i = e[i].nxt){
int v = e[i].to;if(v != fat)dfs(v, u);
}
}
int lca(int x, int y){
if(dep[x] < dep[y])swap(x, y);
while(dep[x] > dep[y])x = fa[x][lg[dep[x] - dep[y]] - 1];
if(x == y)return x;
for(int i = lg[dep[x]] - 1 ; i >= 0 ; i --){
while(fa[x][i] != fa[y][i])
x = fa[x][i],y = fa[y][i];
}return fa[x][0];
}
int main(){
n = read();m = read();s = read();
for(int i = 1 ; i < n ; i ++)
x = read(),y = read(),add(x, y);
for(int i = 1 ; i <= n ; i ++)lg[i] = lg[i >> 1] + 1;
dfs(s, 0);
for(int i = 1 ; i <= m ; i ++){
x = read();y = read();
write(lca(x, y));putchar('\n');
}
return 0;
}树链剖分求 LCA
树剖就是把树剖分成若干条不相交的链,目前常用做法是剖成轻重链。
所以我们定义 $siz(x)$ 为以 $x$ 为根结点的子树的结点个数。对于每个结点 $x$,在它的所有子结点中寻找一个结点 $y$ 使得对于 $y$ 的兄弟节点 $z$,都有$siz(y)\ge siz(z)$。此时 $x$ 就有一条重边连向 $y$,有若干条轻边连向他的其他子结点(比如 $z$)。这样的话,树上的不在重链上的边的数量就会大大减少。
然后我们每次求 LCA 的时候就可以判断两点是否在同一链上,可以分为两种情况:
-
如果两点在同一条链上,我们只要找到这两点中深度较小的点输出就行了。
-
如果两点不在同一条链上,那就找到深度较大的点令它等于它所在的重链链端的父节点即为 $x=fa(vis(x))$,直到两点到达同一条链上,输出两点中深度较小的点。
for(int i = 1 ; i <= m ; i ++){
x = read();y = read();
while(vis[x] != vis[y]){
if(dep[vis[x]] >= dep[vis[y]])x = fa[vis[x]];
else y = fa[vis[y]];
}
if(dep[x] < dep[y])write(x);
else write(y);
putchar('\n');
}附上完整代码。
#include <iostream>
#define MAXN 500005
int n, m, s, x, y;
struct edge{int to, nxt;}e[MAXN << 1];
int head[MAXN], cnt;
int dep[MAXN], siz[MAXN], son[MAXN], fa[MAXN];
int dfn[MAXN], vis[MAXN];
int tot, ans;
int read(){
int t = 1, x = 0;char ch = getchar();
while(!isdigit(ch)){if(ch == '-')t = -1;ch = getchar();}
while(isdigit(ch)){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * t;
}
void write(int x){
if(x < 0){putchar('-');x = -x;}
if(x >= 10)write(x / 10);
putchar(x % 10 ^ 48);
}
void add(int u, int v){
e[++cnt].to = v;e[cnt].nxt = head[u];head[u] = cnt;
e[++cnt].to = u;e[cnt].nxt = head[v];head[v] = cnt;
}
void dfs1(int now, int fat, int deep){
dep[now] = deep;siz[now] = 1;fa[now] = fat;int maxson = -1;
for(int i = head[now] ; i != 0 ; i = e[i].nxt){
int v = e[i].to;
if(v != fat){
dfs1(v, now, deep + 1);siz[now] += siz[v];
if(siz[v] > maxson){
maxson = siz[v];son[now] = v;
}
}
}
}
void dfs2(int now, int fat, int top){
dfn[now] = ++tot;vis[now] = top;
if(son[now] != 0){
dfs2(son[now], now, top);
for(int i = head[now] ; i != 0 ; i = e[i].nxt){
int v = e[i].to;
if(v != fat && v != son[now])dfs2(v, now, v);
}
}
}
int main(){
n = read();m = read();s = read();
for(int i = 1 ; i < n ; i ++)
x = read(),y = read(),add(x, y);
dfs1(s, 0, 1);dfs2(s, 0, s);
for(int i = 1 ; i <= m ; i ++){
x = read();y = read();
while(vis[x] != vis[y]){
if(dep[vis[x]] >= dep[vis[y]])x = fa[vis[x]];
else y = fa[vis[y]];
}
if(dep[x] < dep[y])write(x);
else write(y);
putchar('\n');
}
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号