学习笔记:斜率优化 DP
斜率优化
引入
首先给出一种更加简单的优化。考虑一个这样的的式子:$$ f_i=\min\limits_{0\le j<i}\left\{f_j+g_j+h_i\right\} $$ 不难看出,这个式子中的每一项只会与 $i$,$j$ 中的一个有关。显然可以转化为:$$ f(i)=\min\limits_{0\le j<i}\left\{f_j+g_j\right\}+h_i $$ 具体地,,我们可以考虑在转移的同时维护一个值 $minval=f_j+g_j$。对于每一次转移,我们先令 $f_i=minv+h_i$,再令 $minv=min(minv,f_j+g_j)$,这样就实现了 $O(n)$ 的转移。
然而,对于以下这种含有同时与 $i$,$j$ 有关的项的式子,这种优化就显得有些力不从心了:$$ f(i)=\min\limits_{0\le j<i}\left\{f_j+g_i+h_{i+j}\right\} $$ 在这种情况下,我们就需要考虑更优的做法了。
实现
首先搬一道例题。
形式化题意:给定一个长度为 $n$ 的序列 $x$,将这个序列分成若干块。
具体地,每一块的权值为 $aX^2+bX+c$,其中 $a$,$b$,$c$ 是给定的系数。
对于 $X$,我们定义当前块的区间为 $[l,r]$,则 $X=\sum^r_{i=l}x_i$。
试找出一种方案使得 $\sum X$ 最大,并求出这个最大值。
我们可以很快地写出一个状态转移方程:$$ f_i=\min\limits_{0\le j<i}\left\{f_j+a\times(g_i-g_j)^2+b\times(g_i-g_j)+c\right\} \\ g_i=g_{i-1}+x_i \\ $$ 然而这个式子暴力转移的时间复杂度为 $O(n^2)$,稳稳 TLE。
考虑斜率优化。首先浅浅推导一下:$$ f_i=\min\limits_{0\le j<i}\left\{f_j+a\times(g_i-g_j)^2+b\times(g_i-g_j)+c\right\} \\ f_i=\min\limits_{0\le j<i}\left\{f_j+a\times g_i^2-2\times a\times g_i\times g_j+a\times g_j^2+b\times g_i-b\times g_j+c\right\} \\ $$ 显然某些项只与 $i$ 有关,我们将它们都提出来:$$ f_i+a\times g_i^2+b\times g_i+c=\min\limits_{0\le j<i}\left\{f_j-2\times a\times g_i\times g_j+a\times g_j^2-b\times g_j\right\} \\ $$ 对于一些只与 $j$ 有关的项,显然无论如何这些项都不会随 $i$ 的变化而变化。
我们令 $h_j=f_j+a\times g_j^2-b\times g_j$,
则原式化为 $f_i+a\times g_i^2+b\times g_i=\min\limits_{0\le j<i}\left\{h_j-2\times a\times g_i\times g_j\right\}$,
再令 $s_i=-2\times a\times g_i$,
则原式化为 $f_i+a\times g_i^2+b\times g_i+c=\min\limits_{0\le j<i}\left\{h_j+s_i\times g_j\right\}$,
再分别令 $y=f_i+a\times g_i^2+b\times g_i+c$,$x=g_j$,$k=s_i$,$b=h_j$。则原式化为:$$ y=kx+b $$ 显然这就是直线的斜截式方程。
考虑如何将 $k$ 值(即 $s_i$)最大化。
如果 $j_1<j_2$ 且 $j_1$ 不比 $j_2$ 优,当且仅当 $h_{j_1}+s_i\times g_{j_1}\le h_{j_2}+s_i\times g_{j_2}$,
移项得 $s_i\times (g_{j_1}-g_{j_2})\le h_{j_2}-h_{j_1}$,
由于序列中的每个数都是非负数,所以 $g_{j_2}>g_{j_1}$,即 $g_{j_1}-g_{j_2}<0$,
不等式左右两边同时除以 $g_{j_1}-g_{j_2}$ 得:$$ s_i\le \frac{h_{j_2}-h_{j_1}}{g_{j_1}-g_{j_2}} \\ $$ 即$$ k\le \frac{h_{j_2}-h_{j_1}}{g_{j_1}-g_{j_2}} \\ $$ 由 $s_i=-2\times a\times g_i$ 得:$$ -2\times a\times g_i\le \frac{h_{j_2}-h_{j_1}}{g_{j_2}-g_{j_1}} \\ $$ 不等式左右两边同时乘 $-1$ 得:$$ -\frac{h_{j_2}-h_{j_1}}{g_{j_1}-g_{j_2}}\le 2\times a\times g_i \\ $$ 可以发现,不等式右边是一个斜率的表达式。更具体地,假设在平面直角坐标系上有两个点 $A(g_{j_1},h_{j_1})$,$B(g_{j_2},h_{j_2})$,那么 $\frac{h_{j_2}-h_{j_1}}{g_{j_2}-g_{j_1}}$ 此时就等价于过 $A$,$B$ 两点的直线的斜率。此时可以采用斜率优化。
首先提炼一下之前推式子得到的结论:如果两个点相连所成的直线的斜率不大于 $2\times g_i$,那么前面的点所对应的 $j$ 就必然不是最优决策点;反之,后面的点所对应的 $j$ 就必然不是最优决策点。
先来考虑一下 $3$ 个点的简化情况:如下图所示,显然有 $k_{12}>k_{23}$。
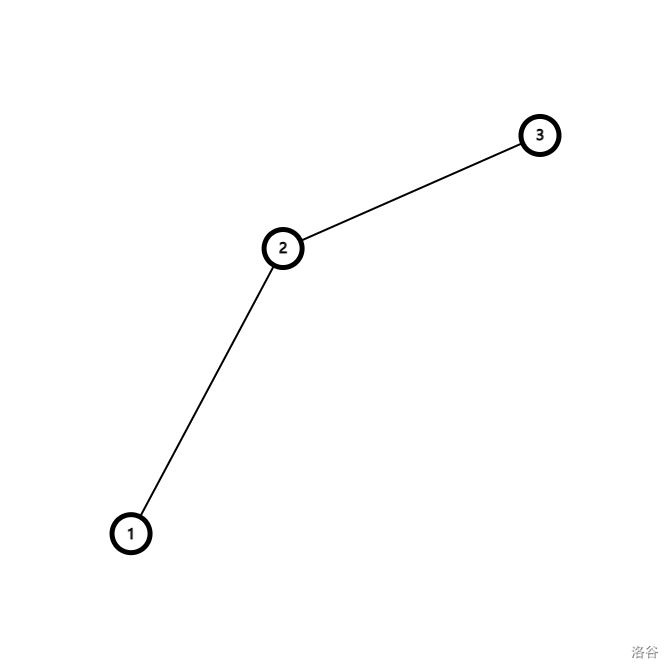
图中的每一个点都对应着一个 $j$。
可以发现,无论如何 $2$ 都不会成为最优决策点。
证明:
- $k_{23}>k$ 时,$2$ 才有可能成为最优决策点,此时有 $l_{23}>k$。
- $k_{12}>k$ 时,$2$ 才有可能成为最优决策点,此时有 $l_{12}\le k$。
又 $l_{12}>l_{23}$,所以不存在任意一个实数 $k$ 使得 $l_{23}>k$ 且 $l_{12}\le k$。
综上所述,$2$ 无论如何都不能成为最优决策点。证毕。
所以这个点已经寄了,我们可以直接将它删去。
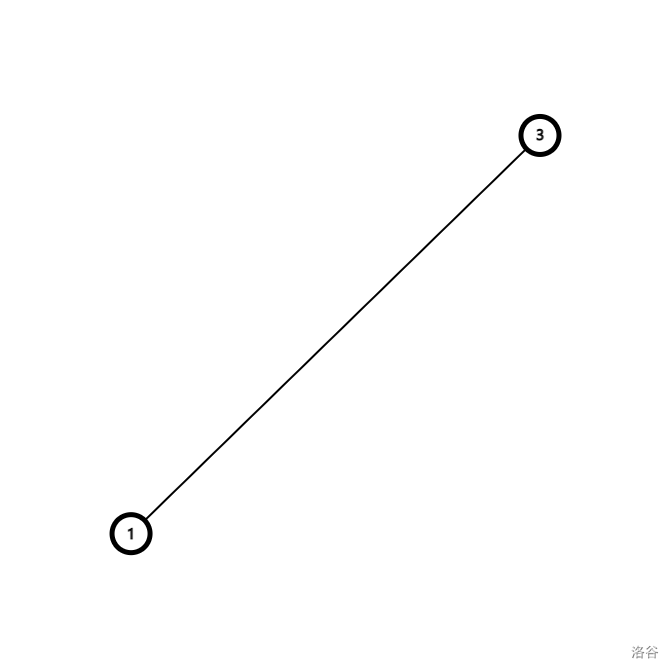
我们已经完美解决了 $3$ 个点的情况,现在让我们试着将结论推广到题目的一般情况。
可以发现,如果存在三个横坐标递增的点,满足前两个点的斜率大于等于后两个点的斜率,那么就可以删去中间的那个点。
所以,如果我们处理出一个不可删点的点集的斜率数组(每相邻两个数的斜率),那么这个数组必然是递增的。
不难发现,在一个不可删点的点集中,最优决策点 $j$ 满足:
- 点 $j-1$ 与点 $j$ 相连所成直线的斜率不大于 $k$。
- 点 $j$ 与点 $j+1$ 相连所成直线的斜率大于 $k$。
不难看出,这些点所成直线的斜率具有单调性,考虑通过二分答案来寻找最优决策点。
具体地,我们枚举 $i$,维护不可删点点集 $A$。设 $A$ 的长度为 $len$,两个点 $i$,$j$ 相连所成直线的斜率为 $k_{ij}$。
- 二分答案找到最优决策点 $j$。
- 执行状态转移。
- 不停弹出队尾直到:$k_{A_{len-1}A_{len}}\le k_{A_{len}i'}\vee A\le 1$,这里的 $i'$ 指的是 $i$ 的对应点。
- 将 $i'$ 加入 $A$ 中。
总的时间复杂度为 $O(n\log n)$。
斜率优化的精髓在于不可删点点集的单调性。正是因为这个单调性,我们才能采用二分去快速寻找最优决策点,从而将时间复杂度优化为 $O(n\log n)$。
对于一些特定的题目,我们可以去掉 $\log$。如对于本题(特别行动队)而言,$k$ 是有单调性的;所以,每次我们可以不停地删去队头,直到队头满足最优决策点的性质;删完之后队头就是最优决策点。此时,每个元素至多入队一次出队一次,时间复杂度 $O(n)$。
现在来看看这道题的代码。
斜率优化的代码历来非常短,甚至连1KB都没有,但是细节非常多。斜率优化的注意事项非常重要,这里有必要阐述一下:
- 斜率优化可能会爆精度,比较两个斜率的时候可以交叉相乘。
- 如果不可删点点集的大小是 $1$ 就不用再删点了。
- 在开始转移之前不可删点点集中有且仅有一个数 $0$。
- 输出不要用 double,不然会自动转化为科学计数法的形式。
- 计算斜率必须 long double,除非采用交叉相乘法。
- 只有 $k$ 具有单调性时才能用队列,否则只能 $O(n\log n)$ 二分答案。
通常来说 $O(n^2)$ 的暴力转移都不难,可以考虑用对拍来查错(但是笔者现在忘得差不多了,这里提一嘴,先鸽着)。
#include <iostream>
#define int long long
#define double long double
#define MAXN 1000005
using namespace std;
int n, a, b, c;
int x[MAXN], f[MAXN], g[MAXN];
int q[MAXN], head = 1, tail = 1;
int read(){
int t = 1, x = 0;char ch = getchar();
while(!isdigit(ch)){if(ch == '-')t = -1;ch = getchar();}
while(isdigit(ch)){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * t;
}
double getx(int x){return g[x];}
double gety(int x){return a * g[x] * g[x] - b * g[x] + f[x];}
double getk(int x, int y){return (gety(y) - gety(x))/(getx(y) - getx(x));}
signed main(){
n = read();a = read();b = read();c = read();
for(int i = 1 ; i <= n ; i ++)x[i] = read();
for(int i = 1 ; i <= n ; i ++)g[i] = g[i - 1] + x[i];
for(int i = 1 ; i <= n ; i ++){
while(head < tail && (a << 1) * g[i] <= getk(q[head], q[head + 1]))head++;
int j = q[head];
f[i] = f[j] + a * (g[i] - g[j]) * (g[i] - g[j]) + b * (g[i] - g[j]) + c;
while(head < tail && getk(q[tail - 1], q[tail]) <= getk(q[tail], i))tail--;
q[++tail] = i;
}
cout << f[n] << endl;return 0;
}一些练习
Luogu P5785,Luogu P3195
这里顺便给出 Luogu P3195 的代码:
#include <iostream>
#define int long long
#define double long double
#define MAXN 50005
using namespace std;
int n, l, c[MAXN];
double f[MAXN], g[MAXN];
int q[MAXN], head = 1, tail = 1;
int read(){
int t = 1, x = 0;char ch = getchar();
while(!isdigit(ch)){if(ch == '-')t = -1;ch = getchar();}
while(isdigit(ch)){x = (x << 1) + (x << 3) + (ch ^ 48);ch = getchar();}
return x * t;
}
double geta(int x){return g[x] + x;}
double getb(int x){return geta(x) + l + 1;}
double getx(int x){return getb(x);}
double gety(int x){return f[x] + getb(x) * getb(x);}
double getk(int x, int y){return (gety(x) - gety(y))/(getx(x) - getx(y));}
signed main(){
n = read();l = read();
for(int i = 1 ; i <= n ; i ++)c[i] = read();
for(int i = 1 ; i <= n ; i ++)g[i] = g[i - 1] + c[i];
for(int i = 1 ; i <= n ; i ++){
while(head < tail && geta(i) * 2 > getk(q[head], q[head + 1]))head++;
f[i] = f[q[head]] + (geta(i) - getb(q[head])) * (geta(i) - getb(q[head]));
while(head < tail && getk(i, q[tail - 1]) < getk(q[tail - 1], q[tail]))tail--;
q[++tail] = i;
}
cout << (long long)f[n] << endl;return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号