学习笔记:四边形不等式优化
四边形不等式优化 DP
引入
首先来看一下区间 DP 的状态转移方程:$$ f(l,r)=\min\limits_{l\le k\le r}\left\{f(l,k)+f(k+1,r)\right\}+w(l,r) $$ 对于这样一个状态转移方程,通常来说我们的做法是:
- 枚举长度 $len$;
- 枚举左指针 $l$;
- 计算右指针 $r=l+len-1$;
- 在区间范围内枚举决策点 $k$;
不难看出,对于这样一种策略,它的时间复杂度通常是 $O(n^3)$(一共约 $O(n^2)$ 个状态,每一次状态转移需要约 $O(n)$ 的时间)。然而,如果上式中的 $w(l,r)$ 满足一些性质,我们可以通过一些办法在 $O(n^2)$ 内解决它。
实现
首先需要满足一些性质:
第一是区间包含单调性,即若 $l\le l'\le r'\le r$,则有 $w(l',r')\le w(l,r)$。

这种性质也可以感性理解为:被包含者不大于包含者。
第二是满足四边形不等式,即若 $l\le l'\le r'\le r$,则有 $w(l',r)+w(l,r')\le w(l,r)+w(l',r')$。
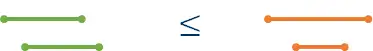
这种性质也可以感性理解为:交叉不大于包含。
引理 1:若 $w(l, r)$ 满足区间包含单调性和四边形不等式,则状态 $f_{l,r}$ 满足四边形不等式。
定义 $g_{k,l,r}=f_{l,k}+f_{k+1,r}+w(l,r)$ 表示当决策为 $k$ 时的状态值,任取 $l_1\leq l_2\leq r_1\leq r_2$,记 $u=\mathop{\arg\min}\limits_{l_1\leq k < r_2}g_{k,l_1,r_2},v=\mathop{\arg\min}\limits_{l_2\leq k < r_1}g_{k,l_2,r_1}$ 分别表示状态 $f_{l_1,r_2}$ 和 $f_{l_2,r_1}$ 的最小最优决策点。
注意到,仅当 $l_2 < r_1$ 时 $v$ 才有意义。因此我们有必要单独考虑 $l_2 = r_1$ 的情形。
首先注意到若 $l_1 = l_2$ 或 $r_1 = r_2$ 时,显然成立。
考虑对区间长度 $r_2 - l_1$ 使用数学归纳法($r_2 - r_1 = 0$ 时,显然成立)。
-
$l_1 < l_2 = r_1 < r_2$(证明过程需要 $w$ 满足区间包含单调性)
-
若 $u < r_1$ 则 $f_{l_1, r_1} \leq f_{l_1, u} + f_{u + 1, r_1} + w(l_1, r_1)$,由归纳法 $f_{u + 1, r_1} + f_{l_2, r_2} \leq f_{u + 1, r_2} + f_{l_2, r_1}$,两式相加再消去相同部分得到(下面最后一个不等式用到了 $w(l_1, r_1) < w(l_1, r_2)$):
$$ f_{l_1, r_1} + f_{l_2, r_2} \leq f_{l_1, u} + f_{u + 1, r_2} + f_{l_2, r_1} + w(l_1, r_1) \leq f_{l_1, r_2} + f_{l_2, r_1} $$
-
若 $u \geq r_1$ 则 $f_{l_2, r_2} \leq f_{l_2, u} + f_{u + 1, r_2} + w(l_2, r_2)$ 由归纳法 $f_{l_1, r_1} + f_{l_2, u} \leq f_{l_1, u} + f_{l_2, r_1}$,两式相加再消去相同部分得到(下面最后一个不等式用到了 $w(l_2, r_2) < w(l_1, r_2)$):
$$ f_{l_1, r_1} + f_{l_2, r_2} \leq f_{l_1, u} + f_{l_2, r_1} + f_{u + 1, r_2} + w(l_2, r_2) \leq f_{l_1, r_2} + f_{l_2, r_1} $$
-
-
$l_1 < l_2 < r_1 < r_2$(仅需要 $w$ 满足四边形不等式)
-
若 $u\leq v$,则 $l_1\leq u< r_1,\ l_2\leq v< r_2$,因此
$$ \begin{aligned} f_{l_1,r_1} \leq g_{u,l_1,r_1} &= f_{l_1,u} + f_{u+1,r_1} + w(l_1,r_1) \\ f_{l_2,r_2} \leq g_{v,l_2,r_2} &= f_{l_2,v} + f_{v+1,r_2} + w(l_2,r_2) \end{aligned} $$
再由 $u+1 \leq v+1 \leq r_1 \leq r_2$ 和归纳假设知
$$ f_{u+1,r_1} + f_{v+1,r_2} \leq f_{u+1,r_2} + f_{v+1,r_1} $$
将前两个不等式累加,并将第三个不等式代入,可得
$$ \begin{aligned} f_{l_1,r_1} + f_{l_2,r_2} & \leq f_{l_1,u} + f_{l_2,v} + f_{u+1,r_1} + f_{v+1,r_2} + w(l_1,r_1) + w(l_2,r_2) \\ & \leq g_{u,l_1,r_2} + g_{v,l_2,r_1} = f_{l_1,r_2} + f_{l_2,r_1} \end{aligned} $$
-
若 $v< u$,则 $l_1\leq v<r_1,l_2\leq u<r_2$,因此
$$ \begin{aligned} f_{l_1,r_1} \leq g_{v,l_1,r_1} &= f_{l_1,v} + f_{v+1,r_1} + w(l_1,r_1) \\ f_{l_2,r_2} \leq g_{u,l_2,r_2} &= f_{l_2,u} + f_{u+1,r_2} + w(l_2,r_2) \end{aligned} $$
再由 $l_1 \leq l_2 \leq v \leq u$ 和归纳假设知
$$ f_{l_1,v} + f_{l_2,u} \leq f_{l_1,u} + f_{l_2,v} $$
将前两个不等式累加,并将第三个不等式代入,可得
$$ \begin{aligned} f_{l_1,r_1} + f_{l_2,r_2} & \leq f_{l_1,u} + f_{l_2,v} + f_{v+1,r_1} + f_{u+1,r_2} + w(l_1,r_2) + w(l_2,r_1) \\ & \leq g_{u,l_1,r_2} + g_{v,l_2,r_1} = f_{l_1,r_2} + f_{l_2,r_1} \end{aligned} $$
-
综上所述,两种情形均有 $f_{l_1,r_1} + f_{l_2,r_2} \leq f_{l_1,r_2} + f_{l_2,r_1}$,即四边形不等式成立。
定理 1:若状态 $f$ 满足四边形不等式,记 $m_{l,r}=\min\{k:f_{l,r} = g_{k,l,r}\}$ 表示最优决策点,则有
$$ m_{l,r-1} \leq m_{l,r} \leq m_{l+1,r} \qquad (l + 1 < r) $$
记 $u = m_{l,r},\ k_1=m_{l,r-1},\ k_2=m_{l+1,r}$,分情况讨论:
-
若 $k_1>u$,则 $u+1 \leq k_1+1 \leq r-1 \leq r$,因此根据四边形不等式有
$$ f_{u+1,r-1} + f_{k_1+1,r} \leq f_{u+1,r} + f_{k_1+1,r-1} $$
再根据 $u$ 是状态 $f_{l,r}$ 的最优决策点可知
$$ f_{l,u} + f_{u+1,r} \leq f_{l,k_1} + f_{k_1+1, r} $$
将以上两个不等式相加,得
$$ f_{l,u} + f_{u+1,r-1} \leq f_{l,k_1}+f_{k_1+1,r-1} $$
即 $g_{u,l,r-1} \leq g_{k_1,l,r-1}$,但这与 $k_1$ 是最小的最优决策点矛盾,因此 $k_1\leq u$。
-
若 $u>k_2$,则 $l\leq l+1 \leq k_2\leq u$,根据四边形不等式可得
$$ f_{l,k_2} + f_{l+1,u} \leq f_{l,u} + f_{l+1, k_2} $$
再根据 $k_2$ 是状态 $f_{l+1, r}$ 的最优决策点可知
$$ f_{l+1,k_2} + f_{k_2+1, r} \leq f_{l+1,u} + f_{u+1,r} $$
将以上两个不等式相加,得
$$ f_{l,k_2}+f_{k_2+1,r} \leq f_{l,u} + f_{u+1,r} $$
即 $g_{k_2,l,r} \leq g_{u,l,r}$,但这与 $u$ 是最小的最优决策点矛盾,因此 $u \leq k_2$。
因此,如果在计算状态 $f_{l,r}$ 的同时将其最优决策点 $m_{l,r}$ 记录下来,那么我们对决策点 $k$ 的总枚举量将降为
$$ \sum_{1\leq l<r\leq n} m_{l+1,r} - m_{l,r-1} = \sum_{i=1}^n m_{i,n} - m_{1,i}\leq n^2 $$
所以为什么要叫四边形不等式呢?我也不知道。
也许是因为这个不等式的形式与四边形对边长度和小于等于对角线长度和的形式非常类似(严格地说,这里不能取等号,因为取等号时四边形会退化)。
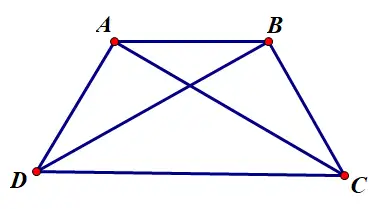
具体地,对于下图而言:$$
dis(A,D)+dis(B,C)\le dis(A,C)+dis(B,D)
$$
还有两个非常神奇的结论:
- 当 $w(l,r)$ 同时满足这两个条件时,$f(l,r)$ 也将符合四边形不等式。
- 如果 $f(l,r)$ 满足四边形不等式,假设 $g(l,r)$ 为 $f(l,r)$ 的最优决策点,那么 $g(l,r-1)\le g(l,r)\le g(l,r+1)$。
什么是最优决策点?考虑 $f(l,r)=\min\limits_{l\le k\le r}\left\{f(l,k)+f(k+1,r)\right\}+w(l,r)$,我们将使得 $f(l,k)+f(k+1,r)$ 取得最小值的 $k$ 值称为 $f(l,r)$ 的最优决策点。
从某种意义上来说,将所有的最优决策点构成一个矩阵时,结论 $2$ 可以证明最优决策点矩阵每一行和每一列都是单调不减的。实际上这才是这个优化的核心。你甚至可以选择不去证明四边形不等式,而是通过打表猜出这个结论(只要能写代码谁关心结论)。
利用结论,我们可以在 DP 的过程中记录最优决策点,这样,我们对于每个状态点,枚举的范围就从 $l\le k<r$ 缩小到了 $g(l,r-1)\le k\le g(l+1,r)$。
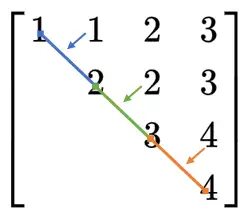
区间 DP 的顺序是从主对角线开始,一条条对角线地往上转移的。在上图中,对于每一条对角线,考察它枚举的区间,可以发现每两个相邻的区间只有一个元素重叠,所以处理每条对角线需要花费 $O(n)$ 的时间,处理所有对角线也就只需要 $O(n^2)$ 的时间。
for(int i = 1 ; i <= n ; i ++)g[i][i] = i; // 初始化边界决策点
for(int len = 1 ; len <= n ; len ++)
for(int i = 1 ; i <= n - len + 1 ; i ++){
int j = i + len - 1;
for(int k = g[i][j - 1] ; k <= g[i + 1][j] ; k ++) // 利用结论缩小范围
if(f[i][k] + f[k + 1][j] + w[i][j] < f[i][j]){
f[i][j] = f[i][k] + f[k + 1][j] + w[i][j]; // 更新 dp 数组
g[i][j] = k; // 更新决策点
}
}哪些二元函数符合四边形不等式呢?通常具有如下性质:
性质 1:若函数 $w_1(l,r),w_2(l,r)$ 均满足四边形不等式(或区间包含单调性),则对于任意 $c_1,c_2\geq 0$,函数 $c_1w_1+c_2w_2$ 也满足四边形不等式(或区间包含单调性)。
性质 2:若存在函数 $f(x),g(x)$ 使得 $w(l,r) = f(r)-g(l)$,则函数 $w$ 满足四边形恒等式。当函数 $f,g$ 单调增加时,函数 $w$ 还满足区间包含单调性。
性质 3:设 $h(x)$ 是一个单调增加的凸函数,若函数 $w(l,r)$ 满足四边形不等式并且对区间包含关系具有单调性,则复合函数 $h(w(l,r))$ 也满足四边形不等式和区间包含单调性。
性质 4:设 $h(x)$ 是一个凸函数,若函数 $w(l,r)$ 满足四边形恒等式并且对区间包含关系具有单调性,则复合函数 $h(w(l,r))$ 也满足四边形不等式。
例如,在经典的石子合并问题中, $w(l,r)=S(r)−S(l−1)$ ,稍作推导或根据结论2可以知道,它符合四边形恒等式和区间包含单调性,所以可以使用四边形不等式优化DP。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号