学习笔记：斯特林数

斯特林数

第二类斯特林数

为什么先介绍第二类斯特林数？因为第一类没学 虽然被称作「第二类」，第二类斯特林数却在斯特林的相关著作和具体数学中被首先描述，同时也比第一类斯特林数常用得多。

第二类斯特林数（斯特林子集数）$\begin{Bmatrix}n\\ k\end{Bmatrix}$，也可记做 $S(n,k)$，表示将 $n$ 个两两不同的元素，划分为 $k$ 个互不区分的非空子集的方案数。

递推式

$$ \begin{Bmatrix}n\\ k\end{Bmatrix}=\begin{Bmatrix}n-1\\ k-1\end{Bmatrix}+k\begin{Bmatrix}n-1\\ k\end{Bmatrix} $$

边界是 $\begin{Bmatrix}n\\ 0\end{Bmatrix}=[n=0]$。

考虑用组合意义来证明。

我们插入一个新元素时，有两种方案：

• 将新元素单独放入一个子集，有 $\begin{Bmatrix}n-1\\ k-1\end{Bmatrix}$ 种方案；
• 将新元素放入一个现有的非空子集，有 $k\begin{Bmatrix}n-1\\ k\end{Bmatrix}$ 种方案。

根据加法原理，将两式相加即可得到递推式。

通项公式

$$ \begin{Bmatrix}n\\m\end{Bmatrix}=\sum\limits_{i=0}^m\dfrac{(-1)^{m-i}i^n}{i!(m-i)!} $$

使用容斥原理证明该公式。设将 $n$ 个两两不同的元素，划分到 $i$ 个两两不同的集合（允许空集）的方案数为 $G_i$，将 $n$ 个两两不同的元素，划分到 $i$ 个两两不同的非空集合（不允许空集）的方案数为 $F_i$。

显然

$$ \begin{aligned} G_i&=i^n\\ G_i&=\sum\limits_{j=0}^i\binom{i}{j}F_j \end{aligned} $$

根据二项式反演

$$ \begin{aligned} F_i&=\sum\limits_{j=0}^{i}(-1)^{i-j}\binom{i}{j}G_j\\ &=\sum\limits_{j=0}^{i}(-1)^{i-j}\binom{i}{j}j^n\\ &=\sum\limits_{j=0}^{i}\dfrac{i!(-1)^{i-j}j^n}{j!(i-j)!} \end{aligned} $$

考虑 $F_i$ 与 $\begin{Bmatrix}n\\i\end{Bmatrix}$ 的关系。第二类斯特林数要求集合之间互不区分，因此 $F_i$ 正好就是 $\begin{Bmatrix}n\\i\end{Bmatrix}$ 的 $i!$ 倍。于是

$$ \begin{Bmatrix}n\\m\end{Bmatrix}=\dfrac{F_m}{m!}=\sum\limits_{i=0}^m\dfrac{(-1)^{m-i}i^n}{i!(m-i)!} $$

同一行第二类斯特林数的计算

「同一行」的第二类斯特林数指的是，有着不同的 $i$，相同的 $n$ 的一系列 $\begin{Bmatrix}n\\i\end{Bmatrix}$。求出同一行的所有第二类斯特林数，就是对 $i=0..n$ 求出了将 $n$ 个不同元素划分为 $i$ 个非空集的方案数。

根据上面给出的通项公式，卷积计算即可。该做法的时间复杂度为 $O(n \log n)$。

同一列第二类斯特林数的计算

「同一列」的第二类斯特林数指的是，有着不同的 $i$，相同的 $k$ 的一系列 $\begin{Bmatrix}i\\k\end{Bmatrix}$。求出同一列的所有第二类斯特林数，就是对 $i=0..n$ 求出了将 $i$ 个不同元素划分为 $k$ 个非空集的方案数。

利用指数型生成函数计算。

一个盒子装 $i$ 个物品且盒子非空的方案数是 $[i>0]$。我们可以写出它的指数型生成函数为 $F(x)=\sum\limits_{i=1}^{+\infty}\dfrac{x^i}{i!} = \mathrm{e}^x-1$。经过之前的学习，我们明白 $F^k(x)$ 就是 $i$ 个有标号物品放到 $k$ 个有标号盒子里的指数型生成函数，那么除掉 $k!$ 就是 $i$ 个有标号物品放到 $k$ 个无标号盒子里的指数型生成函数。

$\begin{Bmatrix}i\\k\end{Bmatrix}=\dfrac{\left[\dfrac{x^i}{i!}\right]F^k(x)}{k!}$，$O(n\log n)$ 计算多项式幂即可。

另外，$\exp F(x)=\sum\limits_{i=0}^{+\infty}\dfrac{F^i(x)}{i!}$ 就是 $i$ 个有标号物品放到任意多个无标号盒子里的指数型生成函数（EXP 通过每项除以一个 $i!$ 去掉了盒子的标号）。这其实就是贝尔数的生成函数。

这里涉及到很多「有标号」「无标号」的内容，注意辨析。

第一类斯特林数

第一类斯特林数（斯特林轮换数）$\begin{bmatrix}n\\ k\end{bmatrix}$，也可记做 $s(n,k)$，表示将 $n$ 个两两不同的元素，划分为 $k$ 个互不区分的非空轮换的方案数。

一个轮换就是一个首尾相接的环形排列。我们可以写出一个轮换 $[A,B,C,D]$，并且我们认为 $[A,B,C,D]=[B,C,D,A]=[C,D,A,B]=[D,A,B,C]$，即，两个可以通过旋转而互相得到的轮换是等价的。注意，我们不认为两个可以通过翻转而相互得到的轮换等价，即 $[A,B,C,D]\neq[D,C,B,A]$。

递推式

$$ \begin{bmatrix}n\\ k\end{bmatrix}=\begin{bmatrix}n-1\\ k-1\end{bmatrix}+(n-1)\begin{bmatrix}n-1\\ k\end{bmatrix} $$

边界是 $\begin{bmatrix}n\\ 0\end{bmatrix}=[n=0]$。

该递推式的证明可以考虑其组合意义。

我们插入一个新元素时，有两种方案：

• 将该新元素置于一个单独的轮换中，共有 $\begin{bmatrix}n-1\\ k-1\end{bmatrix}$ 种方案；
• 将该元素插入到任何一个现有的轮换中，共有 $(n-1)\begin{bmatrix}n-1\\ k\end{bmatrix}$ 种方案。

根据加法原理，将两式相加即可得到递推式。

通项公式

第一类斯特林数没有实用的通项公式。

同一行第一类斯特林数的计算

类似第二类斯特林数，我们构造同行第一类斯特林数的生成函数，即

$F_n(x)=\sum\limits_{i=0}^n\begin{bmatrix}n\\i\end{bmatrix}x^i$

根据递推公式，不难写出

$F_n(x)=(n-1)F_{n-1}(x)+xF_{n-1}(x)$

于是

$F_n(x)=\prod\limits_{i=0}^{n-1}(x+i)=\dfrac{(x+n-1)!}{(x-1)!}$

这其实是 $x$ 的 $n$ 次上升阶乘幂，记做 $x^{\overline n}$。这个东西自然是可以暴力分治乘 $O(n\log^2n)$ 求出的，但用上升幂相关做法可以 $O(n\log n)$ 求出。

同一列第一类斯特林数的计算

仿照第二类斯特林数的计算，我们可以用指数型生成函数解决该问题。注意，由于递推公式和行有关，我们不能利用递推公式计算同列的第一类斯特林数。

显然，单个轮换的指数型生成函数为

$F(x)=\sum\limits_{i=1}^n\dfrac{(i-1)!x^i}{i!}=\sum\limits_{i=1}^n\dfrac{x^i}{i}$

它的 $k$ 次幂就是 $\begin{bmatrix}i\\k\end{bmatrix}$ 的指数型生成函数，$O(n\log n)$ 计算即可。

第三类斯特林数

还没学懂，先鸽着。（其实本来就是贺的）

应用

上升幂与普通幂的相互转化

我们记上升阶乘幂 $x^{\overline{n}}=\prod_{k=0}^{n-1} (x+k)$。

则可以利用下面的恒等式将上升幂转化为普通幂：

$$ x^{\overline{n}}=\sum_{k} \begin{bmatrix}n\\ k\end{bmatrix} x^k $$

如果将普通幂转化为上升幂，则有下面的恒等式：

$$ x^n=\sum_{k} \begin{Bmatrix}n\\ k\end{Bmatrix} (-1)^{n-k} x^{\overline{k}} $$

下降幂与普通幂的相互转化

我们记下降阶乘幂 $x^{\underline{n}}=\dfrac{x!}{(x-n)!}=\prod_{k=0}^{n-1} (x-k)$。

则可以利用下面的恒等式将普通幂转化为下降幂：

$$ x^n=\sum_{k} \begin{Bmatrix}n\\ k\end{Bmatrix} x^{\underline{k}} $$

如果将下降幂转化为普通幂，则有下面的恒等式：

$$ x^{\underline{n}}=\sum_{k} \begin{bmatrix}n\\ k\end{bmatrix} (-1)^{n-k} x^k $$

多项式下降阶乘幂表示与多项式点值表示的关系

在这里，多项式的下降阶乘幂表示就是用

$$ f(x)=\sum\limits_{i=0}^nb_i{x^{\underline{i}}} $$

的形式表示一个多项式，而点值表示就是用 $n+1$ 个点

$$ (i,a_i),i=0..n $$

来表示一个多项式。

显然，下降阶乘幂 $b$ 和点值 $a$ 间满足这样的关系：

$$ a_k=\sum\limits_{i=0}^{n}b_ik^{\underline{i}} $$

即

$$ \begin{aligned} a_k&=\sum\limits_{i=0}^{n}\dfrac{b_ik!}{(k-i)!}\\\dfrac{a_k}{k!}&=\sum\limits_{i=0}^kb_i\dfrac{1}{(k-i)!} \end{aligned} $$

这是一个卷积形式的式子，我们可以在 $O(n\log n)$ 的时间复杂度内完成点值和下降阶乘幂的互相转化。

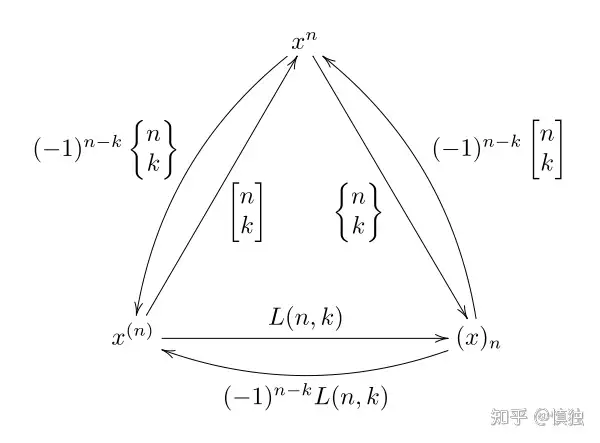
常规幂、上升幂、下降幂通过斯特林数完美的联系在了一起，可以用一张图来概括。