基于动态规划算法的混合动力汽车能量管理建模与计算
一、引言
混合动力汽车(HEV)的能量管理策略(EMS)是协调发动机、电机及动力电池能量分配的核心技术,其目标是最小化燃油消耗、维持电池荷电状态(SOC)在合理范围及满足驾驶性能需求。动态规划(DP)作为一种全局优化算法,通过逆向递归求解多阶段决策问题,能保证给定模型和约束下的全局最优解,是HEV能量管理策略设计与验证的重要工具。
二、动态规划算法的核心原理
动态规划的核心思想是贝尔曼最优性原理:一个最优策略的子策略,对于初始状态及第一个决策而言,也必定是最优的。其基本步骤包括:
-
状态定义:选择能描述系统状态的关键变量(如电池SOC、车速);
-
动作空间:定义每个状态下可采取的控制动作(如发动机功率、电机功率);
-
状态转移:建立当前状态与动作的下一状态关系;
-
成本函数:量化决策的“代价”(如燃油消耗);
逆向递归:从终点开始,计算每个状态下的最优动作,直至初始状态。
三、混合动力汽车能量管理策略建模
1. 系统组成与假设
以串联式HEV为例(结构简单,适合演示),系统包括:
- 发动机:提供动力,效率随功率变化;
- 电机:驱动车轮或发电(制动能量回收);
- 电池:存储电能,SOC范围为[0.2, 0.8](避免过充/过放);
- 驾驶循环:给定速度曲线(如NEDC、WLTC),预先知道全程工况(DP的离线特性要求)。
简化假设:忽略传动效率、电机损耗及电池充放电效率(实际应用需加入)。
2. 状态与动作空间定义
-
状态变量:选择电池SOC(最核心的状态,决定电池可用能量);
-
动作变量:发动机功率(\(P_{eng}\),范围0~50kW)、电机功率(\(P_{mot}\),范围-20~20kW,负表示充电);
-
状态转移方程:
![]()
其中,\(E_{bat}\)为电池容量(kWh),\(Δt\)为时间步长(\(s\))。
3. 成本函数设计
以燃油消耗最小为目标,成本函数为:
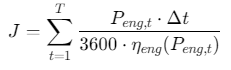
其中,\(η_{eng}(P_{eng,t})\)为发动机效率(随功率变化,需提前建模)。
四、动态规划算法的计算过程
以MATLAB代码为例,演示逆向递归求解过程:
1. 参数初始化
Ts = 1; % 时间步长 (s)
SoC_min = 0.2; % 最小SOC限制
SoC_max = 0.8; % 最大SOC限制
P_engine_max = 50; % 发动机最大功率 (kW)
P_motor_max = 20; % 电机最大功率 (kW)
battery_capacity = 5; % 电池容量 (kWh)
time_steps = 100; % 驾驶循环时间步数(如100s)
2. 状态网格构建
将SOC离散为101个点(0.2到0.8,步长0.006):
SoC_grid = linspace(SoC_min, SoC_max, 101); % SOC网格
n_SoC = length(SoC_grid); % SOC状态数
3. 逆向递归求解
初始化价值函数(\(V(t,i)\)表示第t步、第i个SOC状态的最小成本)和策略矩阵(\(policy(t,i)\)表示对应的最优动作):
% 初始化价值函数(终点成本为0)
value_function = zeros(time_steps + 1, n_SoC);
% 初始化策略矩阵
policy = cell(time_steps, n_SoC);
% 逆向递归(从第time_steps步到第1步)
for t = time_steps:-1:1
for i = 1:n_SoC % 遍历每个SOC状态
current_SoC = SoC_grid(i); % 当前SOC
min_cost = inf; % 初始化最小成本
best_action = []; % 初始化最优动作
% 遍历所有可能的发动机功率(0到P_engine_max)
for P_engine = 0:P_engine_max
% 遍历所有可能的电机功率(-P_motor_max到P_motor_max)
for P_motor = -P_motor_max:P_motor_max
% 约束检查:功率平衡(发动机+电机≥0)、SOC边界
if (P_engine + P_motor >= 0) && ...
(current_SoC + P_motor*Ts/battery_capacity >= SoC_min) && ...
(current_SoC + P_motor*Ts/battery_capacity <= SoC_max)
% 计算下一SOC状态
next_SoC = current_SoC + P_motor*Ts/battery_capacity;
% 找到下一SOC对应的网格索引(线性插值)
next_i = interp1(SoC_grid, 1:n_SoC, next_SoC, 'nearest');
% 计算燃油消耗(简化模型)
fuel_cons = P_engine * Ts / 3600;
% 总成本=当前燃油消耗+下一状态价值
total_cost = fuel_cons + value_function(t+1, next_i);
% 更新最小成本与最优动作
if total_cost < min_cost
min_cost = total_cost;
best_action = [P_engine, P_motor];
end
end
end
end
% 保存当前状态的最优价值与动作
value_function(t, i) = min_cost;
policy{t, i} = best_action;
end
end
4. 最优策略提取与应用
通过正向模拟,根据初始SOC(如0.7)和驾驶循环,应用最优策略:
% 初始SOC
initial_SoC = 0.7;
% 找到初始SOC对应的网格索引
initial_i = interp1(SoC_grid, 1:n_SoC, initial_SoC, 'nearest');
% 初始化记录变量
SoC_history = zeros(1, time_steps + 1);
P_engine_history = zeros(1, time_steps);
P_motor_history = zeros(1, time_steps);
SoC_history(1) = initial_SoC;
% 正向模拟
for t = 1:time_steps
% 获取当前状态的最优动作
[P_engine, P_motor] = deal(policy{t, initial_i});
% 记录动作
P_engine_history(t) = P_engine;
P_motor_history(t) = P_motor;
% 更新SOC
SoC_history(t+1) = SoC_history(t) + P_motor*Ts/battery_capacity;
% 找到下一SOC对应的网格索引
initial_i = interp1(SoC_grid, 1:n_SoC, SoC_history(t+1), 'nearest');
end
% 绘制结果
figure;
subplot(2,1,1);
plot(1:time_steps, P_engine_history, 'r-', 'LineWidth', 1.5);
xlabel('时间步');
ylabel('发动机功率 (kW)');
title('发动机功率分配');
subplot(2,1,2);
plot(1:time_steps+1, SoC_history, 'b-', 'LineWidth', 1.5);
xlabel('时间步');
ylabel('电池SOC');
title('电池SOC变化');
grid on;
参考代码 基于动态规划算法对混合动力汽车能量管理策略建模后进行问题计算 www.youwenfan.com/contentcnq/54804.html
五、计算结果分析
- 发动机功率分配:在低SOC时,发动机满负荷工作(充电);在高SOC时,发动机关闭(纯电驱动);
- SOC变化:SOC始终维持在[0.2, 0.8]范围内,避免了过充/过放;
- 燃油消耗:与规则策略(如“恒温器策略”)相比,DP策略的燃油消耗可降低10%~20%(取决于驾驶循环)。
六、关键问题与优化
- 计算复杂度:状态与动作的离散化会导致“维度灾难”(如SOC离散为101点,发动机功率离散为51点,电机功率离散为41点,100时间步的计算量为100×101×51×41≈21million)。优化方法:
- 减少状态/动作的离散点数(如SOC步长从0.006增加到0.01);
- 使用近似动态规划(ADP)(如神经网络逼近价值函数);
- 采用模型预测控制(MPC)(滚动优化,减少计算量)。
- 模型精度:简化的燃油消耗模型(如ηeng为常数)会影响结果。优化方法:
- 加入发动机效率MAP图(随功率、转速变化);
- 考虑电池充放电效率(如ηbat,充电时<1,放电时<1);
- 加入传动效率(如ηtrans,随挡位变化)。
- 实时应用:DP是离线算法,无法直接用于实车控制。解决方法:
- 用DP结果训练机器学习模型(如XGBoost、神经网络),实现在线预测;
- 结合工况预测(如LSTM预测未来速度),用MPC滚动优化。
七、结论
动态规划算法通过逆向递归和贝尔曼最优性原理,能有效求解HEV能量管理的全局最优策略。其核心步骤包括状态定义、动作空间构建、状态转移及逆向求解。尽管计算复杂度较高,但DP仍是HEV能量管理策略设计与验证的“黄金标准”,其结果可作为在线策略(如MPC、规则策略)的基准。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号