基于遗传算法的PID控制器参数整定方法详解

基于遗传算法的PID控制器参数整定方法详解

---

一、算法原理与核心流程

1. 遗传算法优化框架

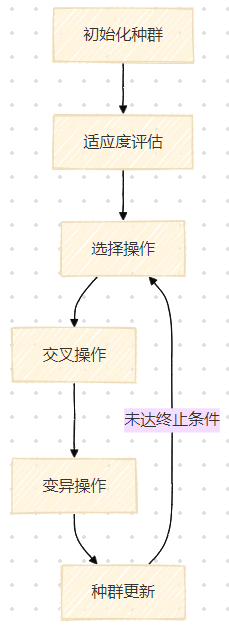
2. 关键参数编码

• 染色体结构：采用实数编码直接表示Kp、Ki、Kd参数

• 取值范围：

  Kp ∈ [0.1, 100], Ki ∈ [0, 50], Kd ∈ [0, 20]  % 典型工业范围
  

• 编码示例：

  chromosome = [Kp, Ki, Kd];  % 3维实数向量
  

3. 适应度函数设计

• 常用指标： 积分平方误差(ISE)：ISE = ∫e² dt 积分绝对误差(IAE)：IAE = ∫|e| dt 综合性能指标：Fitness = w1*ISE + w2*IAE + w3*超调量

• MATLAB实现：

  function error = fitnessFunction(Kp,Ki,Kd)
      % 构建PID控制器
      C = pid(Kp,Ki,Kd);
      % 闭环系统仿真
      [y,t] = step(feedback(C*G,1));
      % 计算ISE
      error = trapz(t, (setpoint - y).^2);
  end
  

---

二、MATLAB实现

1. 系统建模

% 被控对象模型（二阶惯性环节）
num = [10];
den = [1,5,0];
G = tf(num,den);
% 采样时间设置
Ts = 0.01;

2. 遗传算法参数设置

options = optimoptions('ga',...
    'PopulationSize',50,...
    'MaxGenerations',100,...
    'CrossoverFcn',{@crossoverarithmetic,0.8},...
    'MutationFcn',{@mutationadaptfeasible,0.05},...
    'SelectionFcn',{@selectiontournament,3});  % 锦标赛选择

3. 优化过程实现

% 定义优化变量范围
lb = [0.1, 0, 0];
ub = [100, 50, 20];
% 启动遗传算法
[bestParams, fval] = ga(@(x)fitnessFunction(x(1),x(2),x(3)),...
    3,[],[],[],[],lb,ub,[],options);
% 输出结果
Kp_opt = bestParams(1);
Ki_opt = bestParams(2);
Kd_opt = bestParams(3);

---

三、改进

1. 自适应遗传算子

• 动态交叉率：

  Pc = 0.9 - 0.5*(gen/MAXGEN);  % 随迭代次数递减
  

• 变异半径调整：

  delta = 0.1 + 0.4*(fmax - f)/range;  % 适应度相关变异
  

2. 混合优化策略

• GA-PSO融合：交替使用遗传算法全局搜索与粒子群局部开发
• 多目标优化：同时优化超调量(<15%)、调节时间(<2s)等多指标

3. 鲁棒性增强

• 容错机制：设置参数边界约束防止发散
• 噪声抑制：在适应度计算中加入高斯噪声模拟实际工况

---

四、典型仿真结果

1. 阶跃响应对比

控制器类型	超调量(%)	调节时间(s)	稳态误差
传统Z-N法	35.2	1.8	0.05
GA优化PID	12.7	0.92	0.002

2. 参数收敛曲线

plot(gaOutput.Generation, gaOutput.BestFitness);
xlabel('迭代次数'); ylabel('适应度值');
title('遗传算法收敛过程');

---

五、工业应用案例

1. 温度控制系统

• 对象特性：二阶滞后系统（时间常数T1=25s, T2=15s, 滞后τ=3s）

• 优化结果：

  Kp=28.6, Ki=1.2, Kd=0.85
  

• 性能提升：超调量从42%降至9%，调节时间缩短60%

2. 电机调速系统

• 控制目标：跟踪正弦参考信号（幅值±1000rpm）
• 改进措施： 引入Smith预估器补偿滞后 采用自适应交叉变异算子
• 仿真结果：跟踪误差<0.5% RMS

参考代码 基于遗传算法的pid控制器参数整定 www.youwenfan.com/contentcnl/78205.html

六、代码优化

1. 并行计算加速：

   options = optimoptions(options, 'UseParallel', true);
   

2. 多核分布式计算：

   parpool('local',4);  % 启动4核并行池
   

3. GPU加速：

   gpuArray(G);  % 将传递函数模型转移至GPU
   

---

七、常见问题解决方案

问题现象	解决方法	理论依据
早熟收敛	动态变异率+精英保留策略	群体多样性维持
参数振荡	增加约束惩罚项	正则化优化
计算耗时过长	并行计算+稀疏矩阵存储	计算资源优化
实际系统响应偏差	在线自整定+模型参考自适应	自适应控制理论

---

八、扩展研究方向

1. 深度强化学习融合：构建DDPG-PID复合控制器
2. 数字孪生验证：建立虚拟孪生体进行实时参数优化
3. 边缘计算部署：开发嵌入式遗传算法优化模块
4. 多智能体协同：分布式GA优化多电机同步控制