洛谷 P1395：会议 ← 树的重心 + 邻接表

【题目来源】
https://www.luogu.com.cn/problem/P1395

【题目描述】
有一个村庄居住着 n 个村民，有 n-1 条路径使得这 n 个村民的家联通，每条路径的长度都为 1。现在村长希望在某个村民家中召开一场会议，村长希望所有村民到会议地点的距离之和最小，那么村长应该要把会议地点设置在哪个村民的家中，并且这个距离总和最小是多少？若有多个节点都满足条件，则选择节点编号最小的那个点。

【输入格式】
第一行，一个数 n，表示有 n 个村民。
接下来 n-1 行，每行两个数字 a 和 b，表示村民 a 的家和村民 b 的家之间存在一条路径。​​​​​​​

【输出格式】
一行输出两个数字 x 和 y。
x 表示村长将会在哪个村民家中举办会议。
y 表示距离之和的最小值。​​​​​​​

【输入样例】
4
1 2 
2 3 
3 4 

【输出样例】
2 4

【数据范围】
对于 70% 数据 n≤10^3。
对于 100% 数据 n≤5×10^4。

【算法分析】
● “树的重心”性质
性质1‌：某节点是重心等价于其最大子树大小不大于整棵树大小的一半。
性质2‌：树至多有两个重心，若有两个重心则它们相邻，且树的节点数为偶数（可被划分为大小相等的两个分支，每个分支含一个重心）。
性质3：树中所有节点到某点的距离和中，到‌重心‌的距离和是最小的；若有两个重心，树中所有节点到它们的距离和相等。反之，到某点的距离和最小的点一定是重心。

●“树的重心”求解过程
若树的示意图如下所示，则依据定义分析“树的重心”求解过程如下。

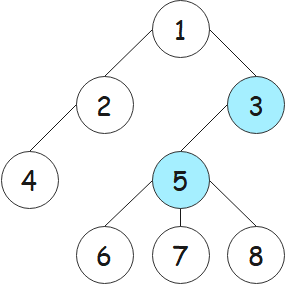
删除结点 1，产生的两个连通块中结点数分别为 2、5，最大值为 5；
删除结点 2，产生的两个连通块中结点数分别为 1、6，最大值为 6；
删除结点 3，产生的两个连通块中结点数分别为 3、4，最大值为 4；
删除结点 4，产生的一个连通块中结点数分别为 7，最大值为 7；
删除结点 5，产生的四个连通块中结点数分别为 1、1、1、4，最大值为 4；
删除结点 6，产生的一个连通块中结点数分别为 7，最大值为 7；
删除结点 7，产生的一个连通块中结点数分别为 7，最大值为 7；
删除结点 8，产生的一个连通块中结点数分别为 7，最大值为 7。
综上，可知 8 个最大值中的最小值为 4，但有两个。也就是说，给出的树有两个重心，分别为结点 3、结点 5。

【算法代码：邻接表一】
for 循环中不用 auto 关键字。

#include <bits/stdc++.h>
using namespace std;

const int N=5e4+5;
vector<int> g[N];
int cnt[N];
int n,dis,cr; //core
int imin=INT_MAX;

void dfs1(int u,int fa) { //find core
    cnt[u]=1;
    int rem=0;
    for(int i=0; i<g[u].size(); i++) {
        int j=g[u][i];
        if(j==fa) continue;
        dfs1(j,u);
        cnt[u]+=cnt[j];
        rem=max(rem,cnt[j]);
    }
    rem=max(rem,n-cnt[u]);

    if(rem<imin || rem==imin && u<cr) {
        imin=rem;
        cr=u;
    }
}

void dfs2(int u,int fa,int dep) { //get distance
    dis+=dep;
    for(int i=0; i<g[u].size(); i++) {
        int j=g[u][i];
        if(j==fa) continue;
        dfs2(j,u,dep+1);
    }
}

int main() {
    cin>>n;
    int a,b;
    for(int i=1; i<n; i++) {
        cin>>a>>b;
        g[a].push_back(b);
        g[b].push_back(a);
    }

    dfs1(1,-1);
    dfs2(cr,-1,0);
    cout<<cr<<" "<<dis;

    return 0;
}

/*
in:
4
1 2
2 3
3 4

out:
2 4
*/

【算法代码二：邻接表二】
for 循环中使用 auto 关键字。

#include <bits/stdc++.h>
using namespace std;

const int N=5e4+5;
vector<int> g[N];
int cnt[N];
int n,dis,cr; //core
int imin=INT_MAX;

void dfs1(int u,int fa) { //find core
    cnt[u]=1;
    int rem=0;
    for(auto j:g[u]) {
        if(j==fa) continue;
        dfs1(j,u);
        cnt[u]+=cnt[j];
        rem=max(rem,cnt[j]);
    }
    rem=max(rem,n-cnt[u]);

    if(rem<imin || rem==imin && u<cr) {
        imin=rem;
        cr=u;
    }
}

void dfs2(int u,int fa,int dep) { //get distance
    dis+=dep;
    for(auto j:g[u]) {
        if(j==fa) continue;
        dfs2(j,u,dep+1);
    }
}

int main() {
    cin>>n;
    int a,b;
    for(int i=1; i<n; i++) {
        cin>>a>>b;
        g[a].push_back(b);
        g[b].push_back(a);
    }

    dfs1(1,-1);
    dfs2(cr,-1,0);
    cout<<cr<<" "<<dis;

    return 0;
}

/*
in:
4
1 2
2 3
3 4

out:
2 4
*/

【参考文献】
https://blog.csdn.net/hnjzsyjyj/article/details/155842302
https://blog.csdn.net/hnjzsyjyj/article/details/155821553
https://blog.csdn.net/hnjzsyjyj/article/details/155837166
https://www.cnblogs.com/triwa/p/19339324
https://blog.csdn.net/hnjzsyjyj/article/details/119912125
https://www.cnblogs.com/hackerchef/p/18750178