古典概型之排列与组合
说明
注意由于是古典概型,适用范围仅限于
- 有限样本空间(样本点数量有限);
- 等可能性(每个样本点的概率相等)。
排列数
引例
问1:在集合
{
a
,
b
,
c
,
d
}
\{a,b,c,d\}
{a,b,c,d}中,任选4个,有多少种排列方式?
答:选第一个有4种可能,当第一个确定了第二个就有3种可能,依次类推:
显然为:
4
×
3
×
2
×
1
=
4
!
=
24
4\times 3\times 2\times 1=4!=24
4×3×2×1=4!=24即24种排列方式
问2:在集合
{
a
,
b
,
c
,
d
}
\{a,b,c,d\}
{a,b,c,d}中,任选3个,有多少种排列方式?
答:选第一个有4种可能,当第一个确定了第二个就有3种可能,当确定了第一个和第二个,那么第三个就有2种可能;
显然为:
4
×
3
×
2
=
4
×
3
×
2
×
1
1
=
4
!
1
=
24
4\times 3\times 2=\frac{4\times 3\times 2\times 1}{1}=\frac{4!}{1}=24
4×3×2=14×3×2×1=14!=24
即24种排列方式
问3:在集合
{
a
,
b
,
c
,
d
}
\{a,b,c,d\}
{a,b,c,d}中,任选2个,有多少种排列方式?
答:选第一个有4种可能,当第一个确定了第二个就有3种可能;
显然为:
4
×
3
=
4
×
3
×
2
×
1
2
×
1
=
4
!
2
!
=
12
4\times 3=\frac{4\times 3\times 2\times 1}{2\times 1}=\frac{4!}{2!}=12
4×3=2×14×3×2×1=2!4!=12
即12种排列方式
问4:在集合
{
a
,
b
,
c
,
d
}
\{a,b,c,d\}
{a,b,c,d}中,任选1个,有多少种排列方式?
答:显然为4种可能,分别是a,b,c,d;显然也可以写作:
4
=
4
×
3
×
2
×
1
3
×
2
×
1
=
4
!
3
!
=
4
4=\frac{4\times 3\times 2\times 1}{3\times 2\times 1}=\frac{4!}{3!}=4
4=3×2×14×3×2×1=3!4!=4
综合上述可归纳总结为: 从 n 个不同元素中取出 m 个元素,按照一定顺序排成一列,出现的可能性个数为排列数。顺序不同即为不同的排列。(英文:Permutation也写作Arrangement),记为
A
(
n
,
m
)
=
P
(
n
,
m
)
=
A
n
m
=
P
n
m
A(n,m)=P(n,m)=A^m_n=P^m_n
A(n,m)=P(n,m)=Anm=Pnm
- 计算公式为:
A n m = n ! ( n − m ) ! A^m_n=\frac{n!}{(n-m)!}\\ Anm=(n−m)!n!
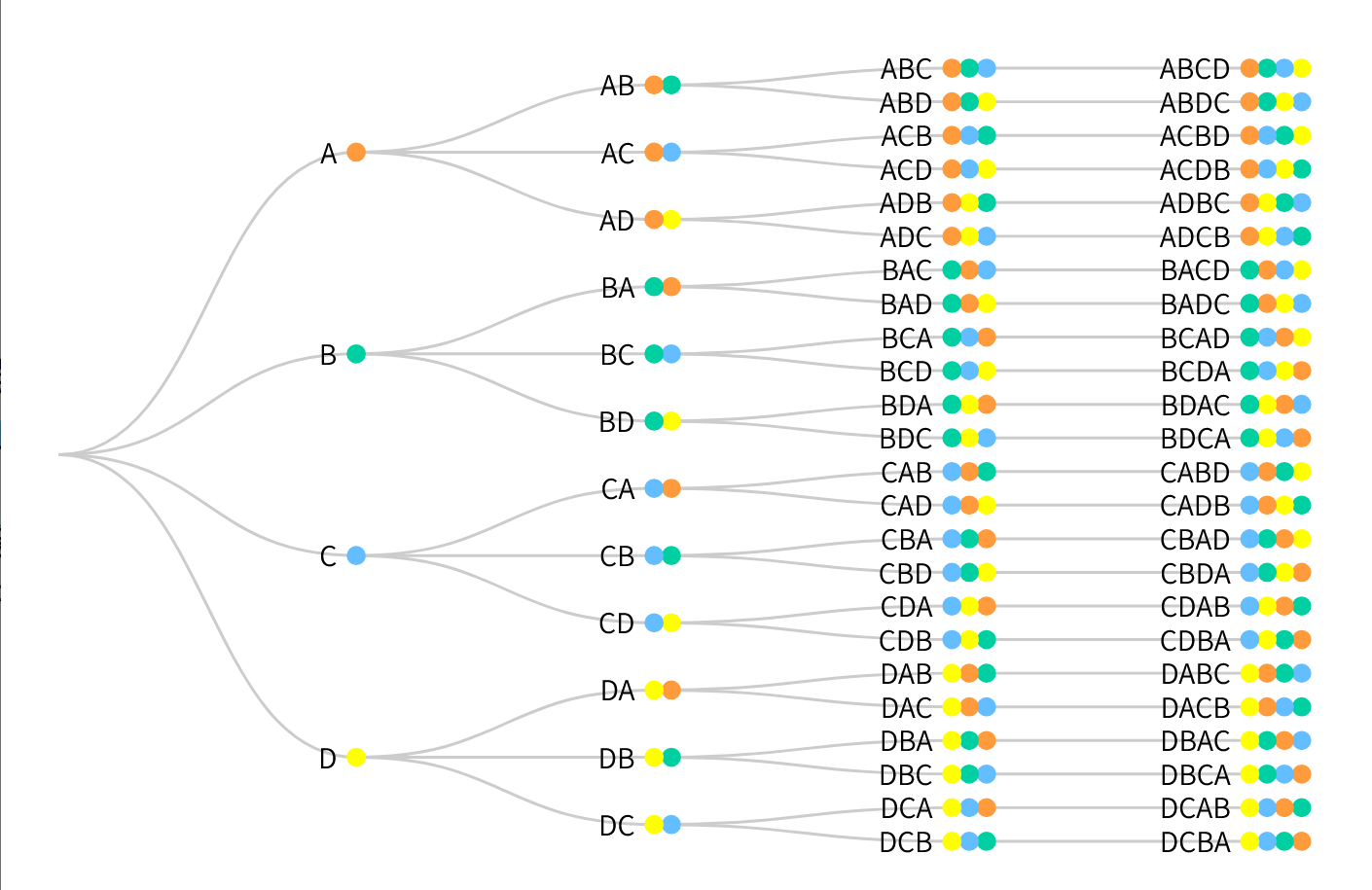
具体可能可以参考下图,与上述对应上;
![在这里插入图片描述]()
组合数
引例
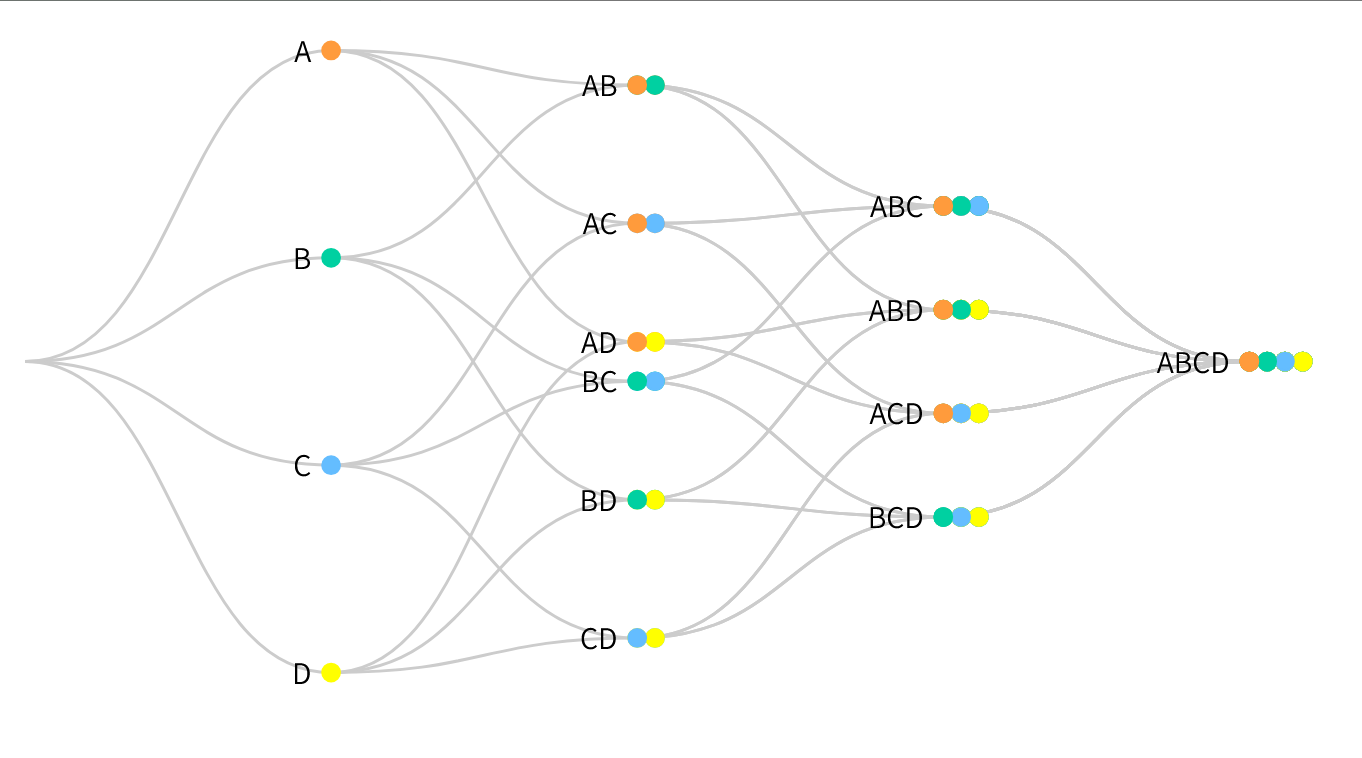
上述例子中,将有序的结果转为无序,即为组合数;
即将
{
a
,
b
}
,
{
b
,
a
}
\{a,b\},\{b,a\}
{a,b},{b,a}视作同一结果:
{
a
,
b
}
\{a,b\}
{a,b};对于上例的24种
{
a
,
b
,
c
,
d
}
\{a,b,c,d\}
{a,b,c,d}的排列来说,都视作一个;
那么上图的结果将变换为下图:
问5:在集合
{
a
,
b
,
c
,
d
}
\{a,b,c,d\}
{a,b,c,d}中,任选4个,有多少种组合方式?
答:1种,即
{
a
,
b
,
c
,
d
}
\{a,b,c,d\}
{a,b,c,d},我们可以换一个方式去思考,这个问题; 其实是问1的答案除以24得到的,这个24显然是在abcd种选择4个元素有多少种排列方式,即
A
4
4
A_4^4
A44
故而可以公式写为:
C
4
4
=
A
4
4
A
4
4
=
1
C_{4}^{4}=\frac{A_4^4}{A_4^4}=1
C44=A44A44=1
问6:在集合
{
a
,
b
,
c
,
d
}
\{a,b,c,d\}
{a,b,c,d}中,任选3个,有多少种组合方式?
对于不含a的所有排列结果,是在bcd种选择3个元素有多少种排列方式,即
A
3
3
A_3^3
A33;
对于不含b的所有排列结果,是在acd种选择3个元素有多少种排列方式,即
A
3
3
A_3^3
A33;
对于不含c的所有排列结果,是在abd种选择3个元素有多少种排列方式,即
A
3
3
A_3^3
A33;
对于不含d的所有排列结果,是在abc种选择3个元素有多少种排列方式,即
A
3
3
A_3^3
A33;
上述的所有的排列结果加起来是问2的答案,即
A
4
3
A_4^3
A43;每个情形都除以
A
3
3
A_3^3
A33,等于之和除以
A
3
3
A_3^3
A33;
即
C
4
3
=
A
3
4
A
3
3
=
24
6
=
4
C_{4}^{3}=\frac{A_3^4}{A_3^3}=\frac{24}{6}=4
C43=A33A34=624=4
归纳总结为:
C
n
m
=
A
n
m
A
m
m
=
n
!
m
!
(
n
−
m
)
!
C^m_n=\frac{A^m_n}{A^m_m}=\frac{n!}{m!(n-m)!}
Cnm=AmmAnm=m!(n−m)!n!
示例
- 某学生需从6门课程中选择3门参加考试,共有多少种选科方式?答: C 6 3 C^{3}_{6} C63
- 从一副标准的52张扑克牌中随机抽取5张,求抽到“同花顺”(同一花色且点数连续)的概率。
答:52随机抽取5张,有 C 52 5 C^{5}_{52} C525种可能,每个花色13张,每个花色可能出现的同花顺数量是10,则所有的同花顺组合一共40种,则 P = 40 C 52 5 P=\frac{40}{C^{5}_{52}} P=C52540 - 掷3个六面骰子,至少有一个骰子显示6的概率是多少?
答:3个骰子中选择1个骰子,有 C 3 1 C^{1}_{3} C31种选法; 假定是6,则另外2个不是6,则一共
C 3 1 × 1 × 5 × 5 C^{1}_{3}\times1\times5\times5 C31×1×5×5的可能;同理可得; 75 + 15 + 1 = 91 75+15+1=91 75+15+1=91,总共是 6 3 6^3 63可能吗,故 P = 91 6 3 P=\frac{91}{6^3} P=6391 - 投掷12次均匀硬币,其中5枚向上的概率是多少?答: C 12 5 C^{5}_{12} C125
定义
- 从 n 个不同元素中取出 m 个元素,不考虑顺序地组合在一起。
- 常见3种写法,第三种常见在二项式系数中
C ( n , m ) = C n m = ( n m ) C(n,m)=C^m_n=\binom{n}{m} C(n,m)=Cnm=(mn)
计算公式
即为排除了重复可能的排列数
C
n
m
=
A
n
m
A
m
m
=
n
!
m
!
(
n
−
m
)
!
C^m_n=\frac{A^m_n}{A^m_m}=\frac{n!}{m!(n-m)!}
Cnm=AmmAnm=m!(n−m)!n!
组合数恒等式
对称性
含义:从 n n n 个元素中选择 m m m 个元素的方法数,等于不选 n − m n−m n−m 个元素的方法数。
(
n
m
)
=
(
n
n
−
m
)
\binom {n}{m}=\binom {n}{n-m}
(mn)=(n−mn)
证明:
(
n
m
)
=
n
!
m
!
(
n
−
m
)
!
(
n
n
−
m
)
=
n
!
n
−
m
!
(
n
−
n
+
m
)
!
=
n
!
(
n
−
m
)
!
m
!
\begin{gather*} \binom {n}{m}=\frac{n!}{m!(n-m)!}\\ \binom {n}{n-m}=\frac{n!}{n-m!(n-n+m)!}=\frac{n!}{(n-m)!m!} \end{gather*}
(mn)=m!(n−m)!n!(n−mn)=n−m!(n−n+m)!n!=(n−m)!m!n!
递推式(帕斯卡恒等式)
含义:从 n n n 个元素中选 k k k 个元素的方法数,等于:
- 不选第 n n n 个元素(即从 n − 1 n−1 n−1 个元素中选 k k k 个),或
- 选第 n n n 个元素(即从 n − 1 n−1 n−1个元素中选 k − 1 k−1 k−1 个)。
这是什么破含义,读不懂;举个例子把:从 { a , b , c , d } \{a,b,c,d\} {a,b,c,d},任选3个,有多少种选法?
显然有:以下4种可能,即 C 4 3 C_4^3 C43,并且问含a和不含a的分别是哪些?
含 a a a元素的
- { a , b , c } , { a , b , d } , { a , c , d } \{a,b,c\},\{a,b,d\},\{a,c,d\} {a,b,c},{a,b,d},{a,c,d}
不含 a a a元素的
- { b , c , d } \{b,c,d\} {b,c,d}
那么包含a元素的问题,可以转换为从 { b , c , d } \{b,c,d\} {b,c,d}中任取2个,有多少种可能,即 C 3 2 C_3^2 C32
那么不包含a元素的问题,可以转换为从 { b , c , d } \{b,c,d\} {b,c,d}任取3个,有多少种可能,即 C 3 3 C_3^3 C33
那么显然可得
C 4 3 = C 3 2 + C 3 3 C_4^3=C_3^2+C_3^3 C43=C32+C33
简单推理可得:帕斯卡恒等式
(
n
m
)
=
(
n
−
1
m
−
1
)
+
(
n
−
1
m
)
\binom {n}{m}=\binom {n-1}{m-1}+\binom {n-1}{m}
(mn)=(m−1n−1)+(mn−1)
下面介绍集合含义,即杨辉三角上的含义;
观察下面的杨辉三角.可见每个元素均为左上,右上2项元素之和:
1
1
1
1
2
1
1
3
3
1
1
4
6
4
1
\begin{align*} & & & & 1 & & & & \\ & & & 1 & & 1 & & & \\ & & 1 & & 2 & & 1 & & \\ & 1 & & 3 & & 3 & & 1 & \\ 1 & & 4 & & 6 & & 4 & & 1 \\ \end{align*}
111413126131411
写成组合数的形式是这样的
C 0 0 C 1 0 C 1 1 C 2 0 C 2 1 C 2 2 C 3 0 C 3 1 C 3 2 C 3 3 C 4 0 C 4 1 C 4 2 C 4 3 C 4 4 \begin{align*} & & & & C_0^0 & & & & \\ & & & C_1^0 & & C_1^1 & & & \\ & & C_2^0 & & C_2^1 & & C_2^2 & & \\ & C_3^0 & & C_3^1 & & C_3^2 & & C_3^3 & \\ C_4^0 & & C_4^1 & & C_4^2 & & C_4^3 & & C_4^4 \\ \end{align*} C40C30C20C41C10C31C00C21C42C11C32C22C43C33C44
当然也可以写成这样,二项式一般这样表达
关于二项式定理,参见: 二项式定理以及证明过程
(
0
0
)
(
1
0
)
(
1
1
)
(
2
0
)
(
2
1
)
(
2
2
)
(
3
0
)
(
3
1
)
(
3
2
)
(
3
3
)
(
4
0
)
(
4
1
)
(
4
2
)
(
4
3
)
(
4
4
)
\begin{align*} & & & & \binom{0}{0} & & & & \\ & & & \binom{1}{0} & & \binom{1}{1} & & & \\ & & \binom{2}{0} & & \binom{2}{1} & & \binom{2}{2} & & \\ & \binom{3}{0} & & \binom{3}{1} & & \binom{3}{2} & & \binom{3}{3} & \\ \binom{4}{0} & & \binom{4}{1} & & \binom{4}{2} & & \binom{4}{3} & & \binom{4}{4} \\ \end{align*}
(04)(03)(02)(14)(01)(13)(00)(12)(24)(11)(23)(22)(34)(33)(44)
可以清晰的看出来,每一项 ( n m ) \binom {n}{m} (mn)均是左上元素 ( n − 1 m − 1 ) \binom {n-1}{m-1} (m−1n−1),以及右上元素 ( n − 1 m ) \binom {n-1}{m} (mn−1)之和;
范德蒙恒等式
引例
问7:同问6:在集合
{
a
,
b
,
c
,
d
}
\{a,b,c,d\}
{a,b,c,d}中,任选3个,有多少种组合方式?;如果拆分成2个非空子集,也是选3个会发生什么?**
答:显然是
(
4
3
)
=
4
\binom{4}{3} =4
(34)=4;若将集合拆成
A
,
B
A,B
A,B;2个不同的非空子集,有以下2组6个方式:
第一组:
A
=
{
a
}
,
B
=
{
b
,
c
,
d
}
;
A
=
{
b
}
,
B
=
{
a
,
c
,
d
}
;
A
=
{
c
}
,
B
=
{
a
,
b
,
d
}
;
A
=
{
d
}
,
B
=
{
a
,
b
,
c
}
;
A={\{a\}},B={\{b,c,d\}};\\ A={\{b\}},B={\{a,c,d\}};\\ A={\{c\}},B={\{a,b,d\}};\\ A={\{d\}},B={\{a,b,c\}};\\
A={a},B={b,c,d};A={b},B={a,c,d};A={c},B={a,b,d};A={d},B={a,b,c};
第二组:
A
=
{
a
,
b
}
,
B
=
{
c
,
d
}
;
A
=
{
a
,
c
}
,
B
=
{
b
,
d
}
;
A={\{a,b\}},B={\{c,d\}};\\ A={\{a,c\}},B={\{b,d\}};\\
A={a,b},B={c,d};A={a,c},B={b,d};
对于第一组而言,要在两组中分别取值,一共取3个,有2种取法
- A取0个,B取3个;也就是 A : ( 1 0 ) ; B : ( 3 3 ) A:\binom{1}{0};B:\binom{3}{3} A:(01);B:(33),共 ( 1 0 ) × ( 3 3 ) = 1 \binom{1}{0}\times \binom{3}{3}=1 (01)×(33)=1种取法;
- A取1个,B取2个; 也就是 A : ( 1 1 ) ; B : ( 3 2 ) A:\binom{1}{1};B:\binom{3}{2} A:(11);B:(23),共 ( 1 1 ) × ( 3 2 ) = 3 \binom{1}{1}\times \binom{3}{2}=3 (11)×(23)=3种取法;
共计
(
1
0
)
×
(
3
3
)
+
(
1
1
)
×
(
3
2
)
=
4
(
种
)
\binom{1}{0}\times \binom{3}{3}+\binom{1}{1}\times \binom{3}{2}=4(种)
(01)×(33)+(11)×(23)=4(种)
对于第二组而言,要在两组中分别取值,一共取3个,有2种取法
- A取1个,B取2个; 也就是 A : ( 2 1 ) ; B : ( 2 2 ) A:\binom{2}{1};B:\binom{2}{2} A:(12);B:(22),共 ( 2 1 ) × ( 2 2 ) = 2 \binom{2}{1}\times \binom{2}{2}=2 (12)×(22)=2种取法;
- A取2个,B取1个; 也就是 A : ( 2 2 ) ; B : ( 2 1 ) A:\binom{2}{2};B:\binom{2}{1} A:(22);B:(12),共 ( 2 2 ) × ( 2 1 ) = 2 \binom{2}{2}\times \binom{2}{1}=2 (22)×(12)=2种取法;
共计
(
2
1
)
×
(
2
2
)
+
(
2
2
)
×
(
2
1
)
=
4
(
种
)
\binom{2}{1}\times \binom{2}{2}+\binom{2}{2}\times \binom{2}{1}=4(种)
(12)×(22)+(22)×(12)=4(种)
通过上例,至少可以看出,一个组合数,可以被任意拆成两部分的非空子集;通过某种方式求和得到;
问8:在集合
{
a
,
b
,
c
,
d
}
\{a,b,c,d\}
{a,b,c,d}中,任选2个,有多少种组合方式?如果拆分成2个非空子集,如何?
答1:
(
4
2
)
=
6
\binom{4}{2}=6
(24)=6
答2:拆法同上应有以下2类;分别考虑:
第一组
:
A
=
{
a
}
,
B
=
{
b
,
c
,
d
}
;
⋯
第二组
:
A
=
{
a
,
b
}
,
B
=
{
c
,
d
}
;
⋯
第一组:\quad A={\{a\}},B={\{b,c,d\}};\\ \cdots\\ 第二组:\quad A={\{a,b\}},B={\{c,d\}};\\ \cdots
第一组:A={a},B={b,c,d};⋯第二组:A={a,b},B={c,d};⋯
对于第一组而言,要在两组中分别取值,一共取2个,有2种取法
- A取0个,B取2个;也就是 A : ( 1 0 ) ; B : ( 3 2 ) A:\binom{1}{0};B:\binom{3}{2} A:(01);B:(23),共 ( 1 0 ) × ( 3 2 ) = 3 \binom{1}{0}\times \binom{3}{2}=3 (01)×(23)=3种取法;
- A取1个,B取1个; 也就是
A
:
(
1
1
)
;
B
:
(
3
1
)
A:\binom{1}{1};B:\binom{3}{1}
A:(11);B:(13),共
(
1
1
)
×
(
3
1
)
=
3
\binom{1}{1}\times \binom{3}{1}=3
(11)×(13)=3种取法;
共计
( 1 0 ) × ( 3 2 ) + ( 1 1 ) × ( 3 1 ) = 6 ( 种 ) \binom{1}{0}\times \binom{3}{2}+\binom{1}{1}\times \binom{3}{1}=6(种) (01)×(23)+(11)×(13)=6(种)
对于第二组而言,要在两组中分别取值,一共取2个,有3种取法
3. A取0个,B取2个;也就是
A
:
(
2
0
)
;
B
:
(
2
2
)
A:\binom{2}{0};B:\binom{2}{2}
A:(02);B:(22),共
(
2
0
)
×
(
2
2
)
=
1
\binom{2}{0}\times \binom{2}{2}=1
(02)×(22)=1种取法;
4. A取1个,B取1个;也就是
A
:
(
2
1
)
;
B
:
(
2
1
)
A:\binom{2}{1};B:\binom{2}{1}
A:(12);B:(12),共
(
2
1
)
×
(
2
1
)
=
4
\binom{2}{1}\times \binom{2}{1}=4
(12)×(12)=4种取法;
5. A取2个,B取0个;也就是
A
:
(
2
2
)
;
B
:
(
2
0
)
A:\binom{2}{2};B:\binom{2}{0}
A:(22);B:(02),共
(
2
2
)
×
(
2
0
)
=
1
\binom{2}{2}\times \binom{2}{0}=1
(22)×(02)=1种取法;
共计
(
2
0
)
×
(
2
2
)
+
(
2
1
)
×
(
2
1
)
+
(
2
2
)
×
(
2
0
)
=
6
(
种
)
\binom{2}{0}\times \binom{2}{2}+\binom{2}{1}\times \binom{2}{1}+\binom{2}{2}\times \binom{2}{0}=6(种)
(02)×(22)+(12)×(12)+(22)×(02)=6(种)
归纳总结,若将组合数
(
m
n
)
\binom{m}{n}
(nm)拆成2部分
(
a
+
b
n
)
,
m
=
a
+
b
\binom{a+b}{n},m=a+b
(na+b),m=a+b,应有这样的猜想:
(
a
+
b
n
)
=
∑
k
=
0
n
(
a
k
)
(
b
n
−
k
)
\binom{a+b}{n}=\sum_{k=0}^{n}\binom{a}{k}\binom{b}{n-k}
(na+b)=k=0∑n(ka)(n−kb)
具体的证明可以用生成函数去证明,主要是用到二项式定理,这里不展开说了;
带权和恒等式
引例
问8:集合
{
a
,
b
,
c
,
d
}
\{a,b,c,d\}
{a,b,c,d}有多少个子集?
答:
2
4
2^4
24个子集,每个元素都有2个选择,即在子集中,或不在子集中;则
2
×
2
×
2
×
2
=
16
2\times2\times2\times2=16
2×2×2×2=16个子集;
从组合数角度:
(
4
0
)
+
(
4
1
)
+
(
4
2
)
+
(
4
3
)
+
(
4
4
)
=
∑
k
=
0
n
(
n
k
)
,
n
=
4
=
1
+
4
+
6
+
4
+
1
=
16
\begin{align*} &\binom{4}{0}+\binom{4}{1}+\binom{4}{2}+\binom{4}{3}+\binom{4}{4}\\ =&\sum_{k=0}^{n}\binom{n}{k} \quad ,n=4 \\ =&1+4+6+4+1\\ =&16 \end{align*}
===(04)+(14)+(24)+(34)+(44)k=0∑n(kn),n=41+4+6+4+116
整理为:
∑
k
=
0
n
(
n
k
)
=
2
n
\sum_{k=0}^{n}\binom{n}{k}=2^n
k=0∑n(kn)=2n
问8:在集合
{
a
,
b
,
c
,
d
}
\{a,b,c,d\}
{a,b,c,d}中,任选3个元素后;再选取1个元素,有多少种选法;
答:即执行先执行4选3,然后执行3选1:;
(
4
3
)
×
(
3
1
)
=
4
×
3
=
12
(
种
)
\binom{4}{3}\times \binom{3}{1}=4 \times 3 = 12(种)
(34)×(13)=4×3=12(种)
或者可以我们4选1,然后在剩余的3个种选2个,即:
(
4
1
)
×
(
3
2
)
=
4
×
3
=
12
(
种
)
\binom{4}{1}\times \binom{3}{2}=4 \times 3 = 12(种)
(14)×(23)=4×3=12(种)
推广到一般情况:从
n
n
n个元素中选
k
k
k若干个元素,再选取
1
1
1个元素,有多少种方法?
(
n
k
)
×
(
k
1
)
=
(
n
1
)
×
(
n
−
1
k
−
1
)
(
n
k
)
×
k
=
n
×
(
n
−
1
k
−
1
)
k
(
n
k
)
=
n
(
n
−
1
k
−
1
)
\begin{align*} \binom{n}{k}\times \binom{k}{1}&=\binom{n}{1}\times \binom{n-1}{k-1}\\ \binom{n}{k}\times k &= n \times \binom{n-1}{k-1}\\ k \binom{n}{k} &= n \binom{n-1}{k-1} \end{align*}
(kn)×(1k)(kn)×kk(kn)=(1n)×(k−1n−1)=n×(k−1n−1)=n(k−1n−1)
利用恒等式
k
(
n
k
)
=
n
(
n
−
1
k
−
1
)
k \binom{n}{k} = n \binom{n-1}{k-1}
k(kn)=n(k−1n−1),展开求和:
∑
k
=
1
n
k
(
n
k
)
=
∑
k
=
1
n
n
(
n
−
1
k
−
1
)
=
n
∑
k
=
0
n
−
1
(
n
−
1
k
)
=
n
⋅
2
n
−
1
\begin{align*} \sum_{k=1}^{n} k \binom{n}{k} &= \sum_{k=1}^{n} n \binom{n - 1}{k - 1} \\ &= n \sum_{k=0}^{n - 1} \binom{n - 1}{k} \\ &= n \cdot 2^{n - 1} \end{align*}
k=1∑nk(kn)=k=1∑nn(k−1n−1)=nk=0∑n−1(kn−1)=n⋅2n−1
求得恒等式
∑
k
=
0
n
k
(
n
k
)
=
n
⋅
2
n
−
1
\sum_{k=0}^{n} k \binom{n}{k} = n \cdot 2^{n - 1}
k=0∑nk(kn)=n⋅2n−1
再次证明:
(
1
+
x
)
n
=
∑
k
=
0
n
(
n
k
)
1
n
−
k
x
k
(
1
+
x
)
n
=
x
0
(
n
0
)
+
x
1
(
n
1
)
+
x
2
(
n
2
)
+
⋯
+
x
n
(
n
n
)
[
(
1
+
x
)
n
]
′
=
[
x
0
(
n
0
)
+
x
1
(
n
1
)
+
x
2
(
n
2
)
+
⋯
+
x
n
(
n
n
)
]
′
n
(
1
+
x
)
n
−
1
=
0
+
1
x
0
(
n
1
)
+
2
x
1
(
n
2
)
+
⋯
+
n
x
n
−
1
(
n
n
)
令
x
→
1
n
⋅
2
n
−
1
=
0
+
1
(
n
1
)
+
2
(
n
2
)
+
⋯
+
n
(
n
n
)
n
⋅
2
n
−
1
=
∑
k
=
0
n
k
(
n
k
)
\begin{align*} (1+x)^n&= \sum_{k=0}^{n}\binom {n}{k}1^{n-k}x^{k}\\ (1+x)^n&= x^0 \binom n0 +x^1 \binom n1+x^2 \binom n2+\cdots +x^n \binom nn\\ [(1+x)^n]'&= [x^0 \binom n0 +x^1 \binom n1+x^2 \binom n2+\cdots +x^n \binom nn]'\\ n(1+x)^{n-1}&= 0+1x^0 \binom n1+2x^1 \binom n2+\cdots +nx^{n-1} \binom nn\\ 令x&\rightarrow 1\\ n \cdot 2^{n-1}&= 0+1\binom n1+2 \binom n2+\cdots +n \binom nn\\ n \cdot 2^{n - 1} &= \sum_{k=0}^{n} k \binom{n}{k}\\ \end{align*}
(1+x)n(1+x)n[(1+x)n]′n(1+x)n−1令xn⋅2n−1n⋅2n−1=k=0∑n(kn)1n−kxk=x0(0n)+x1(1n)+x2(2n)+⋯+xn(nn)=[x0(0n)+x1(1n)+x2(2n)+⋯+xn(nn)]′=0+1x0(1n)+2x1(2n)+⋯+nxn−1(nn)→1=0+1(1n)+2(2n)+⋯+n(nn)=k=0∑nk(kn)
附一个表格参考把
| 序号 | 恒等式名称 | 数学表达式 | 实际含义 |
|---|---|---|---|
| 1 | 对称性 | ( n k ) = ( n n − k ) \binom{n}{k} = \binom{n}{n - k} (kn)=(n−kn) | 从 n n n 个物品中选 k k k 个,与选 n − k n - k n−k 个未被选的物品数量相同。例如:从 10 个学生中选 3 人参赛,与选 7 人未参赛的数量相等。 |
| 2 | 吸收恒等式 | k ( n k ) = n ( n − 1 k − 1 ) k \binom{n}{k} = n \binom{n - 1}{k - 1} k(kn)=n(k−1n−1) | 从 n n n 个物品中选 k k k 个并指定其中一个为“特殊”,等价于先指定一个特殊物品,再从剩余 n − 1 n - 1 n−1 个中选 k − 1 k - 1 k−1 个。例如:从 10 人中选 5 人组成委员会并指定主席,可先选主席再选其余成员。 |
| 3 | 帕斯卡恒等式 | ( n k ) = ( n − 1 k − 1 ) + ( n − 1 k ) \binom{n}{k} = \binom{n - 1}{k - 1} + \binom{n - 1}{k} (kn)=(k−1n−1)+(kn−1) | 从 n n n 个物品中选 k k k 个,分为两种情况:包含某特定物品( ( n − 1 k − 1 ) \binom{n - 1}{k - 1} (k−1n−1))或不包含( ( n − 1 k ) \binom{n - 1}{k} (kn−1))。例如:从 5 个蛋糕中选 2 个,分为包含“巧克力蛋糕”和不包含的情况。 |
| 4 | 二项式定理展开 | ( 1 + 1 ) n = ∑ k = 0 n ( n k ) = 2 n (1 + 1)^n = \sum_{k=0}^{n} \binom{n}{k} = 2^n (1+1)n=k=0∑n(kn)=2n | 从 n n n 个选项中每项选或不选的总方案数为 2 n 2^n 2n。例如:从 5 道菜中任意选或不选,总共有 2 5 = 32 2^5 = 32 25=32 种搭配方式。 |
| 5 | 范德蒙德卷积 | ∑ k = 0 r ( m k ) ( n r − k ) = ( m + n r ) \sum_{k=0}^{r} \binom{m}{k} \binom{n}{r - k} = \binom{m + n}{r} k=0∑r(km)(r−kn)=(rm+n) | 从 m m m 个红球和 n n n 个蓝球中选 r r r 个球,总方案数等于直接从 m + n m + n m+n 个球中选 r r r 个。例如:从 3 个红球和 4 个蓝球中选 2 个,总方案数为 ( 7 2 ) = 21 \binom{7}{2} = 21 (27)=21。 |
| 6 | 组合数求和公式 | ∑ k = 0 n ( n k ) = 2 n \sum_{k=0}^{n} \binom{n}{k} = 2^n k=0∑n(kn)=2n | 所有子集的总数为 2 n 2^n 2n。例如:从 3 门课程中选任意数量的课程,总共有 2 3 = 8 2^3 = 8 23=8 种选择方式。 |
| 7 | 带权求和公式 | ∑ k = 0 n k ( n k ) = n ⋅ 2 n − 1 \sum_{k=0}^{n} k \binom{n}{k} = n \cdot 2^{n - 1} k=0∑nk(kn)=n⋅2n−1 | 所有子集的大小之和为 n ⋅ 2 n − 1 n \cdot 2^{n - 1} n⋅2n−1。例如:从 3 个学生中选任意小组,所有小组的总人数为 3 ⋅ 2 2 = 12 3 \cdot 2^{2} = 12 3⋅22=12。 |
| 8 | 组合数平方和公式 | ∑ k = 0 n ( n k ) 2 = ( 2 n n ) \sum_{k=0}^{n} \binom{n}{k}^2 = \binom{2n}{n} k=0∑n(kn)2=(n2n) | 从 n n n 个男生和 n n n 个女生中各选 k k k 人,总方案数为 ( 2 n n ) \binom{2n}{n} (n2n)。例如:从 3 个男生和 3 个女生中各选 2 人组成小组,总方案数为 ( 6 2 ) = 15 \binom{6}{2} = 15 (26)=15。 |
| 9 | 组合数递推公式 | ( n k ) = n k ( n − 1 k − 1 ) \binom{n}{k} = \frac{n}{k} \binom{n - 1}{k - 1} (kn)=kn(k−1n−1) | 通过递推关系计算组合数。例如:计算 ( 5 2 ) \binom{5}{2} (25),可先计算 ( 4 1 ) = 4 \binom{4}{1} = 4 (14)=4,再乘以 5 / 2 5/2 5/2 得到 10 10 10。 |
| 10 | 组合数与排列的关系 | ( n k ) = P ( n , k ) k ! \binom{n}{k} = \frac{P(n, k)}{k!} (kn)=k!P(n,k) | 从 n n n 个物品中选 k k k 个并排列,除以排列顺序后的组合数。例如:从 4 本书中选 2 本并排列为 P ( 4 , 2 ) = 12 P(4, 2) = 12 P(4,2)=12,组合数为 12 / 2 ! = 6 12 / 2! = 6 12/2!=6。 |



 浙公网安备 33010602011771号
浙公网安备 33010602011771号