【常见分布及其特征(6)】连续型随机变量-指数分布

指数分布

应用场景实例

1. 引例1:
   你站在公交站台等车，已知某路公交车平均每10分钟一班（即每小时6班）。假设车辆到达是完全随机的（比如司机可能因路况随机调整发车时间）。
   问题：

• 如果你现在开始等车，下一辆公交车会在5分钟内到达的概率是多少？
• 如果你已经等了3分钟，接下来再等2分钟就能上车的概率是多少？

2. 引例2:
   你买了一款新手机，商家宣称“平均使用时间8小时”。假设这款手机的电池寿命是完全随机的（比如受温度、使用习惯等随机因素影响）。
   问题：

• 你使用手机时，电池在4小时内耗尽的概率是多少？
• 如果手机已经用了4小时，它还能再坚持4小时的概率是多少？

是不是有一种感觉,和泊松分布很相似?参见: 【常见分布及其特征(4)】离散型随机变量-泊松分布

• 和泊松分布一样,均仅提供了一个参数平均值;

• 回顾一下,泊松分布的均值,描述的平均事件发生率;引例中描述的均值同样如此;

• 泊松分布解决的问题:在固定(单位)时间或空间内，独立随机事件发生次数;

  • 例如每天平均卖出10个包子,问某天卖出0个概率?
  • 每个平均产品有10个缺陷,问某产品有1个缺陷概率?
  • 每小时平均接到10个报警电话;问某小时,接到5个电话的概率?

• 引例中问题:

  • 平均时间间隔10分钟一班;在5分钟时间间隔内等到车的概率?
  • 间隔3分钟后,又间隔2分钟等到车的概率?
  • 平均时间间隔8小时电池耗尽;在4小时时间间隔内电池在耗尽概率?
  • 间隔4小时后,又间隔4小时电池在耗尽概率?

• 整理一下
  泊松分布:平均每天卖10个,求每天卖$x$个概率;
  引例:平均间隔10分发生一次,求间隔$t$分发生的概率(两个事件发生的时间间隔$t$;

更多示例

引例可能不太合适,因为指数分布的概率密度是逐渐下降的,即在例子中,10分钟平均一班,服从指数分布的话,大部分的人等待的时间应该是0-1分左右;重新描述如下
如果发生某一件事件,随着时间的增长,发生的概率逐渐增大(累积分布函数本来就是单调增的);但是增长的速度逐渐放缓(指数下降);

1. 电子元件寿命例子
   电子元件的平均寿命是100h,那么报废是必然事件,随着时间的增长,报废的可能性越来越大;
   当某个电子元件1000h还可继续使用,那必然是小概率事件,查一查有没有其他的报废时间接近1000h的,必然不多; 故而概率密度低,所以随着时间的增长,概率密度降低,而且是呈指数降低;
   在0h多的就报废的是最多的,在0处的概率密度是最高的,这样才满足随着时间的增长,概率密度呈指数增长这一条件;
   在100h时,概率密度下降到一定程度,累积概率增长,
   在1h内报废的,数量极多,发生的概论增长快,
   在10h内报废的,数量增多,但是发生的概论增长减缓,
   在100小时内报废的,数量很多,概率增量进一步减缓
   在1000小时内报废的,几乎是全部数量,概率增量几乎不动了
   在0-1小时报废的,数量最多
   在1-10小时报废的,数量较多
   在100小时左右报废的,数量一般
   大于1000小时报废的,数量极少

2. 银行访客到达例子(这个例子可能更为合适)

• 某银行每日连续营业8小时(480分钟),每一位顾客的到达都是完全随机的,不受饭点一类因素的影响,平均每日到达访客150人(也就是平均3.2分钟来一个顾客);那么某日的到达的情形可能是这样的(截取了前20人的到达情况):
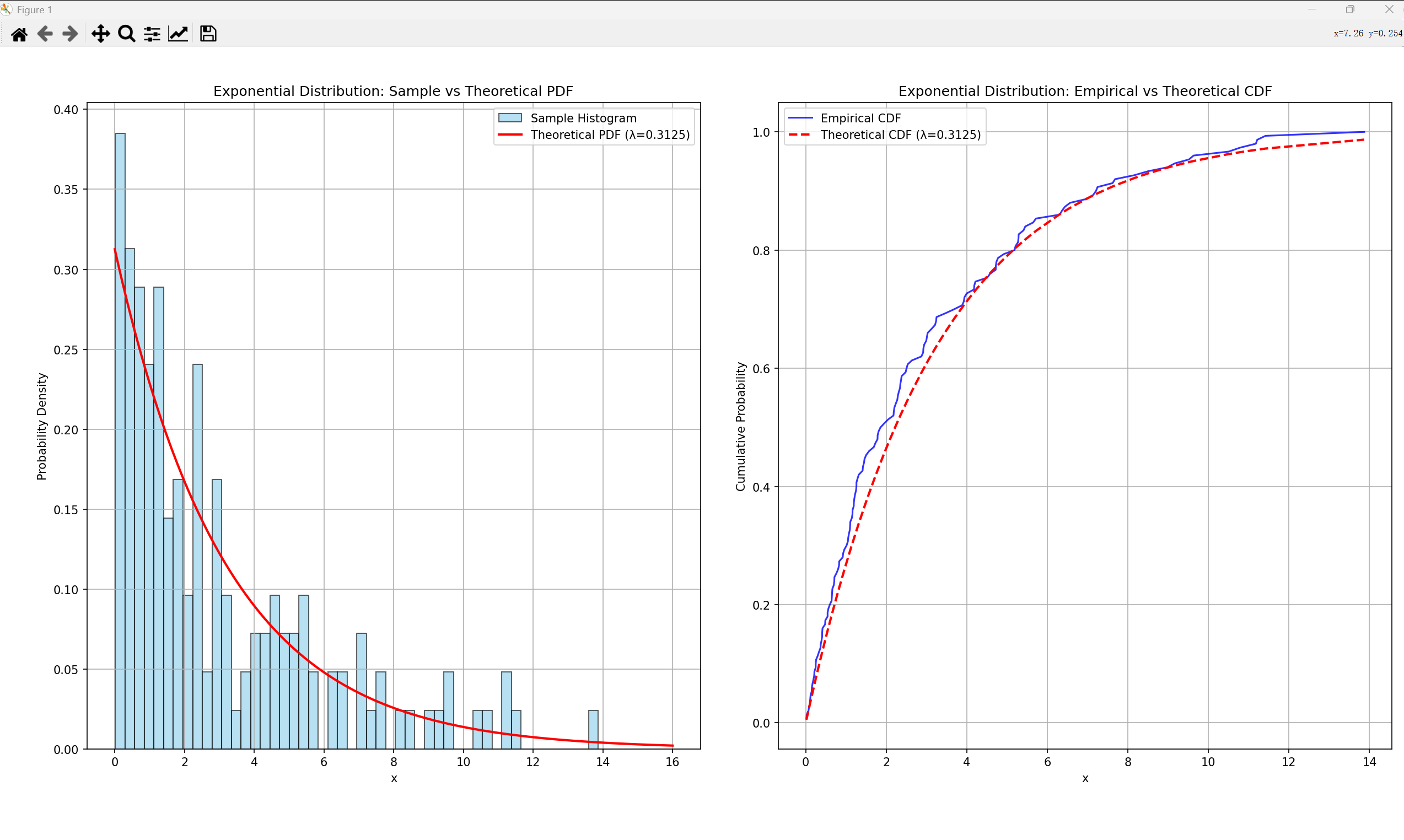
• 可见人的到达接踵而至(时间间隔小于2分钟)的概率比较大,换言之,就是在0处的概率密度较大;等了一下午,一个人也没来的概率极低极低,下面测试数据最长的时间间隔也就是13分钟多点;这是符合主观直觉的

到达序号	到达时刻 (时:分)	间隔时间 (分钟)
1	08:00	-
2	08:01	1.50
3	08:09	9.63
4	08:11	4.21
5	08:13	2.92
6	08:13	0.54
7	08:13	0.54
8	08:13	0.19
9	08:20	6.44
10	08:22	2.94
11	08:24	3.94
12	08:24	0.07
13	08:36	11.21
14	08:41	5.72
15	08:42	0.76
16	08:43	0.64
17	08:44	1.16
18	08:46	2.38
19	08:47	1.81
20	08:48	1.10

• 将时间间隔绘制分布图如下
  
• 以下是完整的时间间隔,单位分钟

# 以下是完整的时间间隔,单位分钟
[ 1.50165789  9.63238858  4.21358622  2.92141617  0.54279959  0.54270813
  0.19148406  6.43593877  2.94106289  3.9400002   0.06655779 11.21138392
  5.71657454  0.7638004   0.64217276  0.64835655  1.16081193  2.38056906
  1.80971861  1.10151358  3.0283868   0.48075049  1.10564964  1.4600871
  1.948591    4.92139524  0.71275476  2.3104933   2.87201511  0.15220432
  2.99306567  0.59827601  0.21524458  9.51580094 10.7860171   5.28746103
  1.16252115  0.32888741  3.68880244  1.8562907   0.41648715  2.18735113
  0.11197991  7.68135324  0.95826489  3.47601856  1.19534906  2.34915487
  2.53191615  0.65404352 11.17698282  4.77518521  8.97630214  7.20688639
  2.91537412  8.15819321  0.29649747  0.69803102  0.14810229  1.25930268
  1.57481693  1.01299342  5.64658517  1.4119264   1.05536909  2.50370267
  0.48607407  5.18554751  0.24792278 13.86926829  4.73434808  0.70892621
  0.01771975  5.40766969  3.9267069   4.17812131  4.72068648  0.24617365
  1.42045655  0.39408033  6.36329463  3.12416381  1.28582016  0.21013781
  1.19196272  1.25860548  4.18520251  3.24764595  6.98320612  2.04501163
  0.40759166  3.9972043   4.57725681  2.63643998  4.71644789  2.17860714
  2.36697228  1.78500542  0.08239288  0.36533579  0.10218778  3.23753456
  1.20766947  2.27339897  7.6200497   0.91756423  1.69050232  4.50799727
  0.8313765   0.25633369  1.09484897  0.56258675  8.49584027  5.28283866
  3.21118141  6.56486314  5.20950061  0.66078552  7.1386029   2.48031969
  5.27151453  7.24557648  1.22473829  0.37309491  0.82779759  1.78258462
  5.45225513  6.30830391  0.02232451  2.28760371  1.72887463  0.80373548
  0.40857725  1.31810746  9.16198759  1.24922817  2.34064898  3.88507833
  1.4463184  11.41695404 10.50243157  0.92819614  2.20050969  1.14537747]

• 附一个生成代码

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import expon

# 参数设置
lambda_val = 0.3125
sample_size = 150
np.random.seed(42)

# 生成样本
samples = np.random.exponential(scale=1/lambda_val, size=sample_size)

# 绘制直方图和理论PDF
plt.figure(figsize=(12, 5))

# 左图：直方图 vs 理论PDF
plt.subplot(1, 2, 1)
plt.hist(samples, bins=50, density=True, alpha=0.6, color='skyblue', edgecolor='black', label='Sample Histogram')
x = np.linspace(0, 5/lambda_val, 1000)
pdf_theoretical = lambda_val * np.exp(-lambda_val * x)
plt.plot(x, pdf_theoretical, 'r-', lw=2, label=f'Theoretical PDF (λ={
     
     lambda_val})')
plt.title('Exponential Distribution: Sample vs Theoretical PDF')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)

# 右图：经验CDF vs 理论CDF
plt.subplot(1, 2, 2)
sorted_samples = np.sort(samples)
y = np.arange(1, sample_size + 1) / sample_size
plt.plot(sorted_samples, y, label='Empirical CDF', color='blue', alpha=0.8)
cdf_theoretical = 1 - np.exp(-lambda_val * sorted_samples)
plt.plot(sorted_samples, cdf_theoretical, 'r--', lw=2, label=f'Theoretical CDF (λ={
     
     lambda_val})')
plt.title('Exponential Distribution: Empirical vs Theoretical CDF')
plt.xlabel('x')
plt.ylabel('Cumulative Probability')
plt.legend()
plt.grid(True)

plt.tight_layout()
plt.show()

推导过程

同时设2个随机变量$T,X$

1. 设两个事件发生的时间间隔为随机变量$T,T\ge 0$;
2. 设每$t$时间间隔发生的事件的次数为随机变量$X,\ge 0$;平均每$t$时间,发生$\lambda$次事件,即$X\sim$