LeetCode 面试经典150题---002
### 169. 多数元素
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。你可以假设数组是非空的,并且给定的数组总是存在多数元素。
n == nums.length
1 <= n <= 5 * 104
-109 <= nums[i] <= 109
这题可太有意思了,意思就是找到众数,并且这个众数的个数是大于n/2的。方法很多,比如(1)哈希表,记录每个元素出现的次数,边记录边判断是否个数>n/2。(2)随机数,随机一个数,判断它的次数是否大于n/2。但是这两种方法属于是正常做法,作为不正常的我们自然要另辟蹊径。
这个数组其实存在这样一种性质,我们把数组中的元素分为两类,一类是众数,另一类是非众数。(1)我们删除一个众数和非众数,其实这个数组本身的性质仍然不变,即众数个数还是>n/2,说明这个操作没有影响。(2)我们删除两个不相等的非众数,数组性质还是不变,并且众数还比原来相对更多了,这是我们乐意看到的。那此时你就想问了,为什么不删除两个相等的数,因为我们的目的是通过两两相消不等的数,每次遇到相等的数就把它看作是众数,遇到不等的就两两相消,这样坐下来最后一定是留下的众数,因为众数的个数永远是最多的(参考刚刚说的两个性质)。
class Solution {
public:
int majorityElement(vector<int>& nums) {
int cnt = 1, candidate = nums[0];
for(int i = 1;i < nums.size();i ++ ){
if(nums[i] != candidate){
cnt --;
if(cnt < 0){
cnt = 1;
candidate = nums[i];
}
}
else{
cnt ++;
}
}
return candidate;
}
};
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
1 <= nums.length <= 105
-231 <= nums[i] <= 231 - 1
0 <= k <= 105
第一种方法,直接开辟一个新的数组,每个元素向右移动k个位置,使用(i + k) % n实现,如下所示:
class Solution {
public:
void rotate(vector<int>& nums, int k) {
int n = nums.size();
vector<int> temp(n);
for(int i = 0;i < n;i ++ ){
temp[(i + k) % n] = nums[i];
}
nums = temp;
}
};
不过题目要求用O(1)的原地算法实现,也就是不能重新开辟数组。可以发现一个规律,最终的数组就是原数组的后k % n个元素移到前面,前n - k % n个元素移到后面,所以直接翻转原数组,然后分别对前后两端再翻转,如下所示:
class Solution {
public:
void rotate(vector<int>& nums, int k) {
k %= nums.size();
reverse(nums.begin(), nums.end());
reverse(nums.begin(), nums.begin() + k);
reverse(nums.begin() + k, nums.end());
}
};
题解还有一种环状替换的方法,没看懂先记录一下
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
1 <= prices.length <= 105
0 <= prices[i] <= 104
题目的意思就是找到数组中的某一段,使得尾部减去首部的元素差值最大,如果差值是负数,则返回0。我们考虑,肯定会在某一天卖出,那我们就循环每一天,只需要维护这一天之前的所有天的最小值,这样对于每一天我们都可以计算出在这一天卖出的话我们的最大利润,每次的最大利润取max就是最终的最大利润。
class Solution {
public:
int maxProfit(vector<int>& nums) {
int mi = 1e5 + 10, res = -1;
for(int num : nums){
mi = min(mi, num);
res = max({res, 0, num - mi});
}
return res;
}
};
1 <= prices.length <= 3 * 1e4
0 <= prices[i] <= 1e4
这题就是你可以买多只股票,但是你买的时间段不能有交集,比如你买入的一只股票,从买入到卖出可以看成一条折线,我们需要找到很多条折线(还要是上升的,因为这样才有利润),并且他们不能相交,画个图吧。
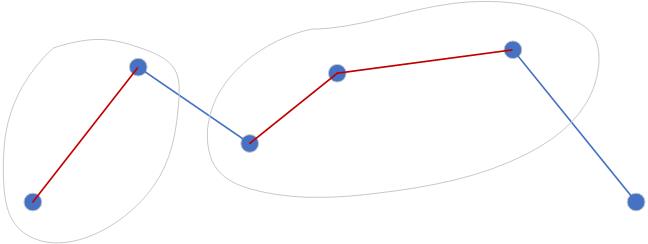
图中每个点分别是股票的价格,红色的线段就是我们需要选取的,因为他们都是上升的,计算它们的差值就可以了。注意计算的过程并不是实际的交易过程。
class Solution {
public:
int maxProfit(vector<int>& nums) {
int res = 0;
for(int i = 1;i < nums.size();i ++ ){
res += max(0, nums[i] - nums[i - 1]);
}
return res;
}
};
题解还用了动态规划,不过没有那么好理解。定义dp[i][0]为第i天未持有股票的最大利润,dp[i][1]为第i天持有股票的最大利润,因为对于某一天,要么就持有股票,要么就未持有股票。(1)dp[i][0]由i-1天未持有股票和i - 1天持有股票但是第i天卖掉了转移而来,即dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + nums[i]。(2)dp[i][1]由i-1天持有股票和i-1天未持有股票但在i天买入股票转移而来,即dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - nums[i])。初始化的时候dp[0][0]=0是显然的,dp[0][1]=-nums[0],最终得到的是dp[n - 1][0]和dp[n - 1][1],显然最后一天不能持有股票,因为没法卖出去了,永远都比最后一天不持有股票的利润低。
class Solution {
public:
int maxProfit(vector<int>& nums) {
int n = nums.size();
int dp[n][2];
dp[0][0] = 0, dp[0][1] = -nums[0];
for(int i = 1;i < n;i ++ ){
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + nums[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - nums[i]);
}
return dp[n - 1][0];
}
};
动态规划问题基本都涉及空间优化,也就是不需要定义dp[n][2],而是直接用变量来存,可以将复杂度从O(n)降低到O(1)。可以发现,dp[i][0]和dp[i][1]永远只跟上一状态有关系,因此我们直接用两个变量记录上一状态。
class Solution {
public:
int maxProfit(vector<int>& nums) {
int n = nums.size();
int dp0 = 0, dp1 = -nums[0];
for(int i = 1;i < n;i ++ ){
int dp0_new = max(dp0, dp1 + nums[i]);
int dp1_new = max(dp1, dp0 - nums[i]);
dp0 = dp0_new;
dp1 = dp1_new;
}
return dp0;
}
};
总结,动态规划的思想还是不会,虽然题解一看就会,可能这就是菜吧。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号