LeetCode 面试经典150题---005

#### 135. 分发糖果
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。
你需要按照以下要求，给这些孩子分发糖果：每个孩子至少分配到 1 个糖果。相邻两个孩子评分更高的孩子会获得更多的糖果。请你给每个孩子分发糖果，计算并返回需要准备的 最少糖果数目 。
n == ratings.length
1 <= n <= 2 * 104
0 <= ratings[i] <= 2 * 104
本题的意思就是对于数组中的元素i，如果它比i-1大，那么它得到的糖果数就要比i-1大1，对于i+1也是一样的。我们首先将答案数组初始化为全1，然后从左到右遍历，如果此时nums[i]>nums[i-1]，则将res[i] = res[i - 1] + 1；遍历完成后，我们只考虑了每个元素比左边元素要大的情况，因此还需要从右往左遍历一遍，考虑每个元素比右边元素要大的情况，并且由于res[i]已经计算过一遍了，因此第二次遍历的时候不能直接更新res[i]，而是要res[i] = max(res[i], res[i + 1] + 1)，保证res[i]对于左右元素都满足条件。

class Solution {
public:
    int candy(vector<int>& nums) {
        int n = nums.size();
        vector<int> res(n, 1);
        int ans = 0;
        for(int i = 1;i < n;i ++ ){
            if(nums[i] > nums[i - 1]) res[i] = res[i - 1] + 1;
        }
        for(int i = n - 2;i >= 0;i -- ){
            if(nums[i] > nums[i + 1]) res[i] = max(res[i], res[i + 1] + 1);
            ans += res[i];
        }
        ans += res[n - 1];
        return ans;
    }
};

定位是困难题，还有一种解法是记忆化搜索，不过不如这个简单，懒得写了，二刷的时候再来查漏补缺吧。

#### 238. 除自身以外数组的乘积

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。请不要使用除法，且在 O(n) 时间复杂度内完成此题。
2 <= nums.length <= 105
-30 <= nums[i] <= 30
保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内
题意比较简单，容易想到的方式是定义一个前缀和后缀数组，用来分别存储i元素之前的所有元素乘积和i元素之后的所有元素乘积。

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        int n = nums.size();
        vector<int> L(n, 1), R(n, 1);
        for(int i = 1;i < n;i ++ ) L[i] = L[i - 1] * nums[i - 1];
        for(int i = n - 2;i >= 0;i -- ) R[i] = R[i + 1] * nums[i + 1];
        vector<int> res(n);
        for(int i = 0;i < n;i ++ ) res[i] = L[i] * R[i];
        return res;
    }
};

但是这个方法的缺点是需要额外定义两个数组来存乘积，空间复杂度为\(O(n)\)。题目说了结果数组不算空间复杂度，那我们就可以好好利用起来，首先从左往右遍历，计算每个元素i的前i-1个元素的乘积，存到结果数组里面；然后从右往左遍历，定义一个变量end，代表遍历到i的时候后n-i-1个元素的乘积，再和结果数组相乘，空间复杂度为\(O(1)\)。

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        int n = nums.size();
        vector<int> res(n);
        res[0] = 1;
        for(int i = 1;i < n;i ++ ) res[i] = res[i - 1] * nums[i - 1];
        int end = 1;
        for(int i = n - 1;i >= 0;i -- ){
            res[i] = res[i] * end;
            end *= nums[i];
        }
        return res;
    }
};

还是比较简单，主要思路很好理解。

#### 134. 加油站

在一条环路上有 n 个加油站，其中第 i 个加油站有汽油 gas[i] 升。你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。给定两个整数数组 gas 和 cost ，如果你可以按顺序绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1 。如果存在解，则 保证 它是 唯一 的。
gas.length == n
cost.length == n
1 <= n <= 105
0 <= gas[i], cost[i] <= 104
很有意思的题，相当于要找到一条环路，使得在前进过程中gas-cost不会小于0。环路问题，我看到的解法是把数组扩展1倍，长度变为2n，这样就转变成了在2n数组中找一条长度为n的子数组，使得过程中不会出现负数。我们定义st和ed为路径的起点和终点，tot为前进过程中的值，需要保证它>=0，如果出现了tot<0，说明从st开始到ed是不可行的，并且st为这段中的任何一个点都不可行，为什么呢，看下图。

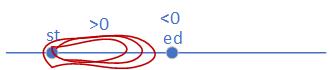
假设st-ed-1的tot都是大于0的，到ed的时候tot就小于0了，因此我们可以发现，st如果为[st,ed]区间的任意一个位置，它们之间的tot都是小于0的，因此以st为头部的后缀都是大于0的，如果st为[st,ed]的任意一个位置，相当于是st-ed的总和（负数）减去sst-st'（正数）,st'就是st-ed的任意一个位置，永远都是负数，因此st可以一直++，直到tot>0，ed每次++即可。

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int n = gas.size();
        vector<int> nums;
        for(int i = 0;i < 2 * n;i ++ ) nums.push_back(gas[i % n] - cost[i % n]);
        int st = 0, ed = 0;
        int tot = 0;
        while(st < n && ed < 2 * n){
            tot += nums[ed];
            while(tot < 0){
                tot -= nums[st];
                st ++;
            }
            if(ed - st + 1 == n) return st;
            ed ++;
        }
        return -1;
    }
};

这题很有意思，环路问题一般都要扩展一倍数组吧...