AlphaTensor论文阅读分析-矩阵乘法优化-强化学习

AlphaTensor论文阅读分析

目前只是大概了解了AlphaTensor的思路和效果，还在不断完善中....

deepmind博客在 https://www.deepmind.com/blog/discovering-novel-algorithms-with-alphatensor

论文是 https://www.nature.com/articles/s41586-022-05172-4

解决"如何快速计算矩阵乘法"的问题

前置知识：Strassen算法，以\(O(n^{2.807})\)复杂度完成矩阵乘法，简要了解其思想的话，就是在\((2,2)*(2,2)\)的矩阵乘法中，使用一些加法组合达到了更少的乘法次数，从而降低了复杂度（可以搜索以了解其思想~）。

问题建模

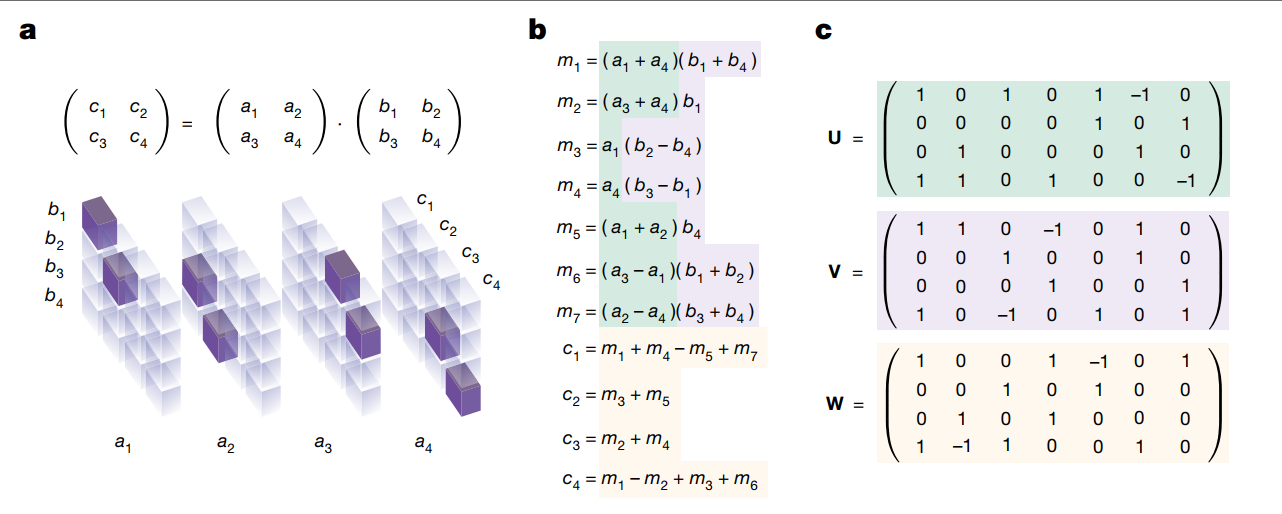
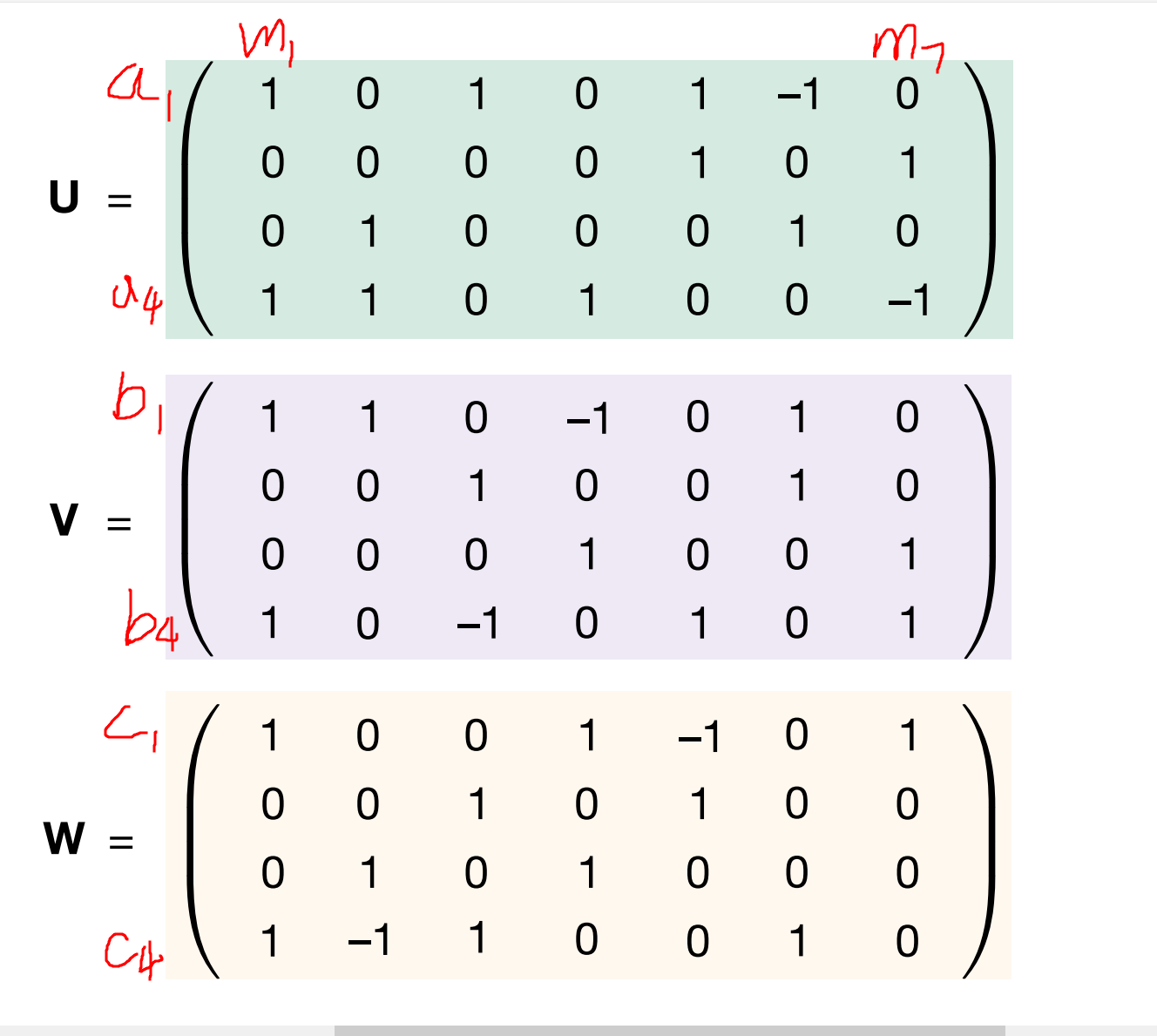
仔细观察上面第一张图，b是strassen计算\((2,2)*(2,2)\)矩阵相乘的方法，c是用tensor来表示a和b他们相乘、组合的逻辑。可以拿u, v的第一列来作为例子。u, v, w三个tensor的意义可以见第二张图。这里需要理解一段时间。

可以发现，每种u,v,w tensor的表示法，就对应着一种矩阵乘法的算法。至于为什么拿Strassen举例，因为ci用ai bi来表示时，只有二阶项，意味着mi就是算完了乘法之后的项，剩余的事情都是线性组合，线性组合的线性组合还是线性组合，因此从mi到ci只需要一次线性组合了。

然后一句话概括矩乘任务就是：在u,v,w张量的空间中进行搜索，找到最优的矩阵乘法表示法。

变成single-player game

\[\tau_n= \sum_{r=1}^R \textbf{u}^{(r)} \otimes \textbf{v}^{(r)} \otimes \textbf{w}^{(r)} \]

In \(2*2*2\) case of Strassen, R is 7. (see the fig.c). RL的目标是最小化 R (i.e. total step)

the size of $\textbf{u}^{(r)} $ is \((n^2, R)\).

$ \textbf{u}^{(1)}$ 是u的第一列: \((1,0,0,1)^T\)

$ \textbf{v}^{(1)}$ 是v的第一列: \((1,0,0,1)^T\)

$\textbf{u}^{(1)} \otimes \textbf{v}^{(1)} = $

\[\begin{bmatrix} 1 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\1 & 0 & 0 & 1 \end{bmatrix}\quad \]

上面矩阵的第一行代表a1，第四行代表a4，第一列代表b1... (1,1)位置出现一个1，表示当前矩阵代表的式子里面有个\(a_1b_1\) ， 上面这个矩阵对应的是m1=(a1+a4)(b1+b4)

$\textbf{u}^{(1)} \otimes \textbf{v}^{(1)} \otimes \textbf{w}^{(1)} $ 就是再结合上ci，哪些ci中包括m1这一项。最终三者外积得到的是\(n*n*n\)的张量，ci对应的\(n*n\)矩阵内记录的就是ci需要哪些ab的乘积项来组合出来。当然，最终需要R个这样的三维张量才能达到正确的矩阵乘法。

(第一步是选择mi如何由ai bi组成，这对应上面那个\(n*n\)的矩阵。第二步是选择ci如何由mi组成，这对应着\(\textbf{w}\)那个\((n^2, R)\)的矩阵。两步合在一起得到R个\(n*n*n\)的三维张量，R个三维张量加起来得到\(\tau_n\)，\(\tau_n\)中挑出ci那一维，对应的矩阵就是ci如何由ai bi组成)。

按照朴素矩阵乘法，\(c_1=a_1*b_1+a_2*b_3\) ，因此，无论采用什么路径， 合计出来的三维张量\(\tau_n\)，在c1这个维度上都必须是

\[\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\0 & 0 & 0 & 0 \end{bmatrix}\quad \]

因此，可以用朴素矩阵乘法算出最终的目标，即\(\tau_n\) 。然后不断搜索\((u^{(t)}, v^{(t)}, w^{(t)})\)，使得他们的外积之和能够拼凑出\(\tau_n\)。

RL

step

在step 0, \(S_0=\tau_n\). (target)

在游戏的step t, player选择一个三元组 \((u^{(t)}, v^{(t)}, w^{(t)})\) : $S_t \leftarrow S_{t-1} - \textbf{u}^{(t)} \otimes \textbf{v}^{(t)} \otimes \textbf{w}^{(t)} $

目标是用最少的步数达到zero tensor \(S_t=\vec 0\)

文中说
constrain \(\{u^{(t)}, v^{(t)}, w^{(t)}\}\) in a user-specified discrete set of coeffients F (\(F= \{-2,-1,0,1,2\}\))， 所以 action space 是 \(\{-2,-1,0,1,2\}^{n^2} \times \{-2,-1,0,1,2\}^{n^2} \times \{-2,-1,0,1,2\}^{n^2}\)。

为了避免游戏被拉得太长: \(R \le R_{limit}\) ( \(R_{limit}\) 步之后终止)

reward:

每一个step: -1 reward （为了找到最短路）

如果在non-zero tensor终止: \(-\gamma(S_{R_{limit}})\) reward
(\(\gamma(S_{R_{limit}})\) 是terminal tensor的rank的上界)

AlphaTensor

有些类似于 AlphaZero

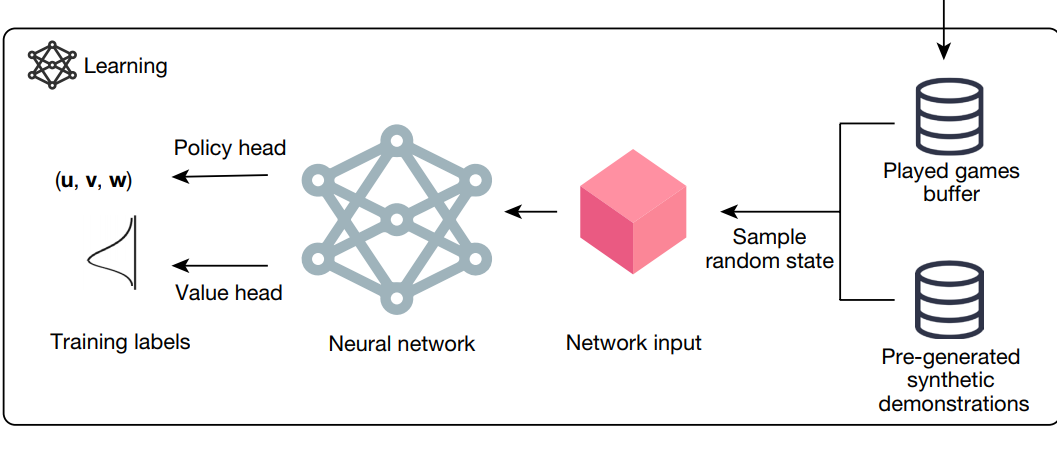
• 一个deep nn 去指导 MCTS.
• state作为输入, policy (action上的一个概率分布) 和 value作为输出

算出最优策略下每一步的action: \(\{(u^{(r)}, v^{(r)}, w^{(r)})\}^R_{r=1}\) 之后，就可以拿uvw用于矩阵乘法了

效果

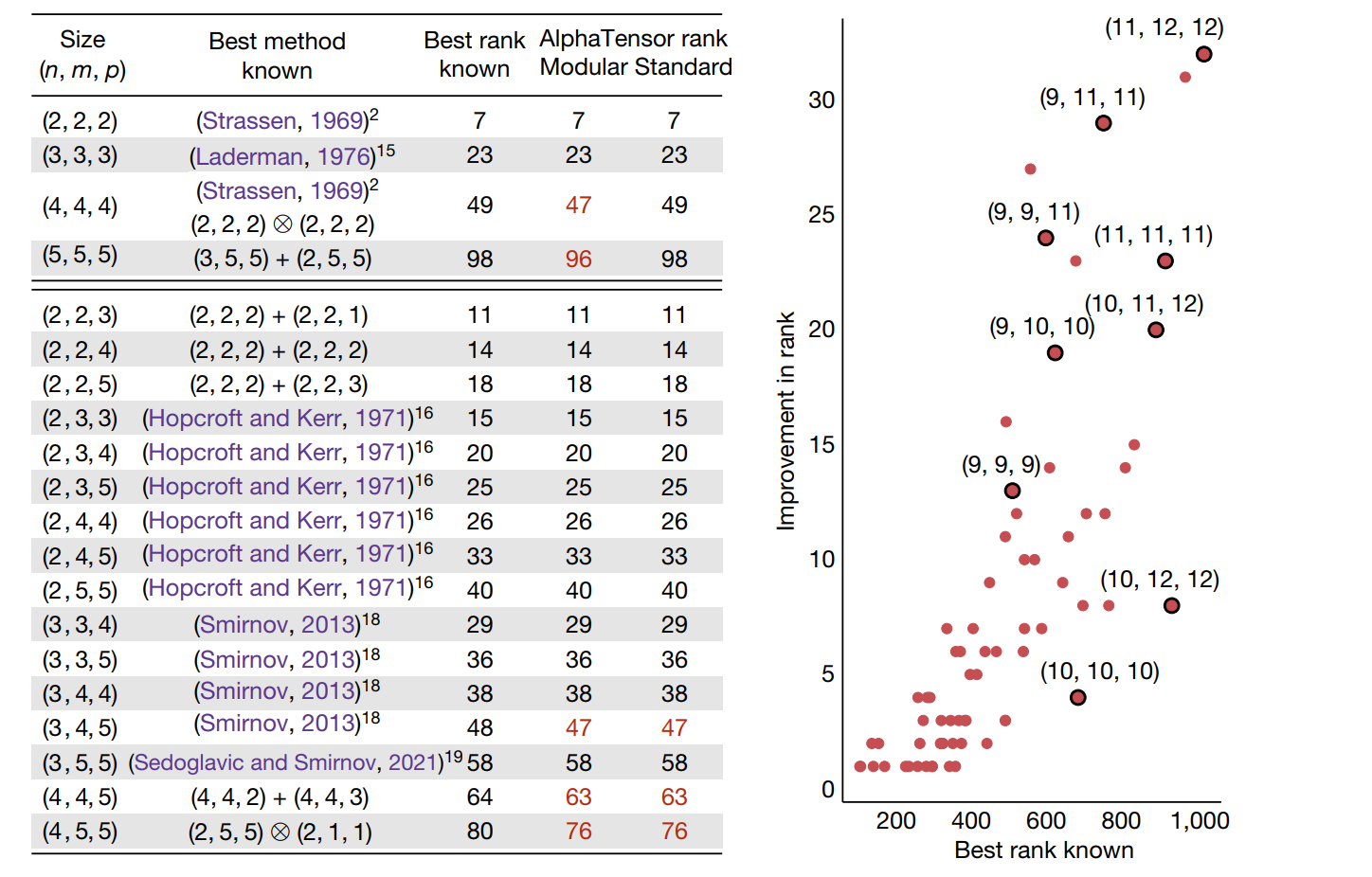
可以看到，AlphaTensor搜索出来的计算方法，在部分矩阵规模上达到了更优的结果，即乘法次数更少。注意一点，上图中的三列数，分别代表之前人类发现的最优乘法次数、模空间下AlphaTensor发现的乘法次数、实数空间下AlphaTensor发现的乘法次数，但是中间一列（modular）是说在模空间(modular arithmetic \(\mathbb{Z}_2\))中得到的最优乘法次数。因此(4,4,4)在标准的实数空间上并没有乘法次数上的优化。

在第四行，(5,5,5)情形下的矩阵乘法，AlphaTensor计算出来的方法可以在博客里面看到，非常复杂，为了减少两次乘法，却耗费了数几十次加法。因此AlphaTensor只能做到渐进时间复杂度更优，在大矩阵情形下达到更快的速度。

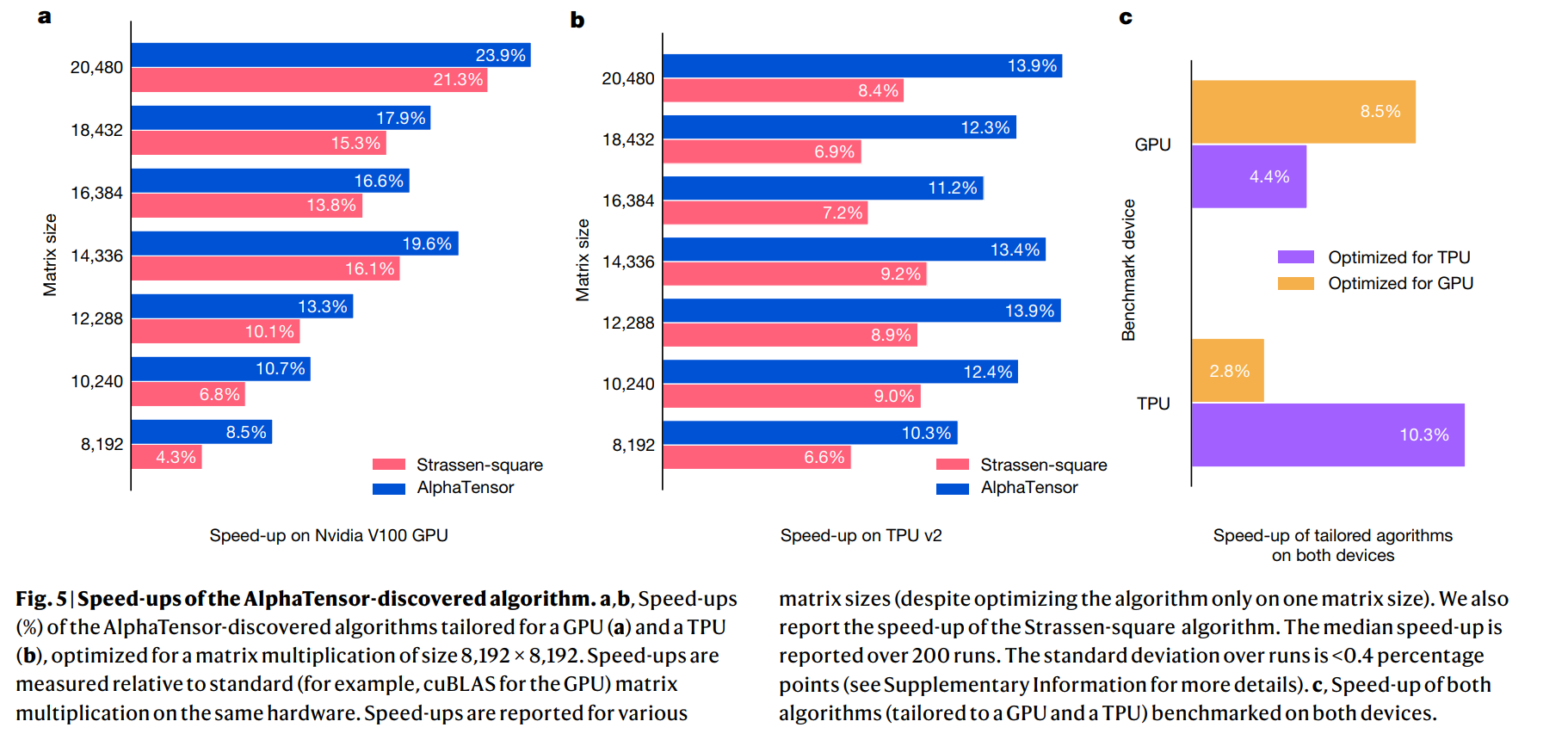
AlphaTensor可以通过修改reward等方式发现定制化算法tailored algorithm。比如在特定的硬件上找到最优的矩阵乘法。

他们在\(8192*8192\)的方阵乘法上进行了测试，采用\(4*4\)分块的方式（这样每个子矩阵的大小就是\(2048*2048\)规模的了），AlphaTensor方法比Strassen的方法在模空间减少了两次矩阵乘法，但是实数空间上的复杂度并没有变化。因此加速比从1.043提升至1.085是由于AlphaTensor-discovered algorithms中存在更适合V100的算法。这说明这一方法相比coppersmith-winograd方法(\(O(n^{2.37})\))那种银河算法更加实用，常数更低，在8192规模的矩阵就能生效了。而且，计算矩阵乘法的Algorithm 1也方便在GPU和TPU上并行。

意义