2022“杭电杯”中国大学生算法设计超级联赛（7）
| 1001 | 1002 | 1003 | 1004 | 1005 | 1006 | 1007 | 1008 | 1009 | 1010 | 1011 | |
| 赛时过题 | O | O | O | ||||||||
| 赛后补题 | O | O | O |
赛后总结：
前几天不知为何状态奇差，学也学不进去，比赛也精神不好，干啥啥不顺。。。最近几场都考崩了害
不过现在调整地差不多了，下次一定！
这场考崩的一个原因是1004卡太久了，是一道结论题，与其卡这题不如早点去做其他可做题，比如1006和1002，三个人只留一个人看这题就够了。
1004、1008两个签到题让我很难受，而且1003我的容斥做法写崩了也让我很难受。。。但是1006明明我是有十分把握的却没有主动去写。。
总的来说考试遇到不顺是很正常的事情，几乎不可能做到每次的签到题都能快速切，不要被签到题搞心态，切记！切不出来先做其他题，别在这题卡死！
赛时排名：
4题末尾：236名
5题末尾：159名
6题末尾：93名
7题末尾：60名
1008 Triangle Game
题目难度：easy
题目大意：一个非退化三角形，三边边长分别为a,b,c。现 Kate 和 Emilico 二人做游戏，每轮需要令三角形的一边长度减去一正整数，使这个三角形退化为线段的一方败。
Kate 先手，双方均采用最优策略，问 Kate 是否会获胜。
赛时经历：
这题考场上有很多人速切了，但是我们一直没找到规律，然后我就去打表了。
一开始一直往奇偶性去找，但却没有想到像这类博弈论题也有很大的概率和异或有关，还是1h的时候才宇彬想到了异或，并迅速找到公式，才做出来。
解题分析：
不妨将a,b,c视为三堆石子，并设a<=b<=c，由于取石子应该是要能取到0的，不妨让A=a-1,B=b-1,C=c-1
则三角形不退化的条件就从 a+b>c ,a+c>b ,b+c>a ⇒ A+B≥C,A+C≥B,B+C≥A
考虑取石子的SG函数：SG= A xor B xor C
结合SG函数的证明过程进行证明：（具体详见[模板]Nim博弈与SG函数）
1、当SG=0时
①如果三个数中有一个数=0（假设为A），则另外两个数相同（假设为B、C），A不可变小，变小B或C都会使三角形退化 ：A+B<C
因此如果三个数有个0则为必败局面。
②如果三个数没有一个数=0，则由于SG=A xor B xor C=0 ，修改任意一个数都会导致SG≠0
2、当SG≠0时
设A xor B xor C=k，并设k的最高位为i。
选择A、B、C中第i位为1的那一个（假设为A），并让A'= A xor k，从而SG'=A' xor B xor C =0
由于A的第i位1变成0，且高位不变，故A肯定是变小的，即A'<A
又由于SG'=0，即A xor B =C , A xor C =B , B xor C =A
从而A+B≥A xor B =C ,A+C ≥A xor C =B , B+C≥B xor C =A (x+y>=x xor y是因为在第t位上如果两位都不为1，则x+y=x xor y；如果两位都为1，则x+y会向高位进位，而x xor y则会为0）
因此A'=A xor k肯定是合法操作
参考代码：
查看代码
/*#if(__cplusplus == 201103L)
#include <unordered_map>
#include <unordered_set>
#else
#include <tr1/unordered_map>
#include <tr1/unordered_set>
namespace std
{
using std::tr1::unordered_map;
using std::tr1::unordered_set;
}
#endif*/
#include<bits/stdc++.h>
using namespace std;
int T,a[10],ans=0;
int main()
{
cin>>T;
while(T--)
{
ans=0;
scanf("%d%d%d",&a[1],&a[2],&a[3]);
if((((a[1]-1)^(a[2]-1))^(a[3]-1))==0)
printf("Lose\n");
else
printf("Win\n");
}
return 0;
}1004 Black Magic
题目难度：easy
题目大意：有二元组(0,0)，(0,1)，(1,0)，(1,1)各若干个，要将其按照某种顺序排列。相邻的两个二元组如果中间那个是1则会合并为一块，如(0,1)+(1,0) -> (0,0)。要求最少得到几块and最多得到几块。
解题思路：
先考虑最少得到几块：
可以发现(1,1)可以完全被(0,1)或(1,0)吞掉，然后(0,1)和(1,0) 一定摆放成形如0110 0110 0110 ... 如果还有剩的(0,1)则摆成01 01 01 01，剩下的(1,0)同理。
注意到(0,0)不可能和任何二元组合并。那么答案就是 v[0][0]+std::max(std::max(v[0][1],v[1][0]),(long long)!!v[1][1])，
再考虑最多得到几块：
由于(1,1)只要当其两边都是0的时候才会被计数，即...0 11 0....
考虑如何让(0,0),(0,1),(1,0)为(1,1)创造尽可能好的条件。
先把(0,0)全部放好，即 00 00 00 ... 00
然后再放(0,1)，发现无论怎么放，(1,1)的计数环境数 没有变化 ，形如：00 01 01 .. 00 ,即11 不能放在01 00和01 01中间，只能放10 00中间
然后再放(1,0)，如果把它放在01的右边，则变成0110,相当于多了一个00，则多了一个11计数环境，但是这个(1,0)会被合并掉不算入计数。最多使答案+1。
如果把它放在x0的右边，则10会被计数，但11计数环境数没有变化，对于...0 10 00 来说，11只能放10 00中间，否则会被吞。一定使答案+1。
这两种情况一比较会发现，最优方案是把它放在x0的后边。
那么最终一定形如 00 10 10 ... 01 01 ... 00 10 10...，11的计数环境数为00的个数+1。
答案为：v[0][0]+v[1][0]+v[0][1]+std::min(v[1][1],v[0][0]+1))
赛时经历：
还是因为状态太差，这题的关键是以00和11作为切入点进行讨论，我比赛的时候昏头昏脑的根本找不到切入点，害，还是靠宇彬才做出来。
参考代码：
查看代码
#include<iostream>
#include<cstdio>
long long v[10][10];
int main()
{
int T;scanf("%d",&T);
while (T--)
{
scanf("%lld%lld%lld%lld",&v[0][0],&v[1][0],&v[0][1],&v[1][1]);
printf("%lld %lld\n",v[0][0]+std::max(std::max(v[0][1],v[1][0]),(long long)!!v[1][1]),
v[0][0]+v[1][0]+v[0][1]+std::min(v[1][1],v[0][0]+1));
}
return 0;
}1003 Counting Stickmen
题目难度：easy-medium
题目大意：给定一棵树，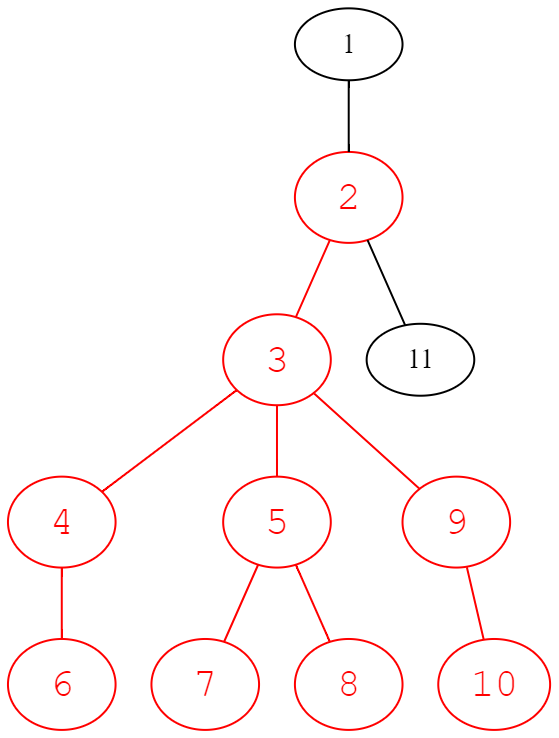
1-2为头，3-4-6和3-9-10为一双手，3-5为身体，5-7和5-8是一双腿。问这个树有几个这样的子图。
解题分析：可以选择一个关键点进行计数。
标答是枚举边作为身体（形如3-5），那么他的两边就比较好讨论。
不过实际上也可以枚举3这个关键点，然后进行容斥计数。
令dp[root][0,1,2]分别表示root作为头的方案数（如图中点2）、作为手的方案数（如图中点4,9），作为腿的方案数（如图中点5）
那么枚举3，答案就是sum0*sum1*sum1*sum2，然后注意容斥即可。
需要注意的是，如果直接容斥，需要讨论非常多的情况，但如果注意到无论手和身体、脚怎么取，头一定是degree[root]-3种方案，那就能大大简化容斥的情况数。
（考试的时候就是因为对容斥理解不深刻，且情况数过多导致没做出来，也是靠宇彬做出来的。。。）
（实际上这题和一般的容斥也不太一样，普通容斥使用加减法，这题用的是乘法，将其理解为若干多项式相乘，再排除需要排除的那些项更好理解）
参考代码：
查看代码
#include<iostream>
#include<cstdio>
#include<vector>
#define For(i,a,b) for(int i=a;i<=b;i++)
const long long mod=998244353;
const int N=5e5+1000;
std::vector<int> To[N];
long long dp[N][5];
long long sum0[N],sum1[N],sum2[N],sum01[N],sum02[N],sum11[N],sum12[N],sum011[N],sum012[N],sum112[N],sum0112[N];
long long power(long long x,long long y)
{
long long ans=1;x%=mod;
while (y)
{
if (y&1) ans=ans*x%mod;
x=x*x%mod;y>>=1;
}
return ans;
}
int main()
{
int T;scanf("%d",&T);
while (T--)
{
int n;scanf("%d",&n);
For(i,1,n) To[i].clear();
For(i,1,n-1)
{
int a,b;scanf("%d%d",&a,&b);
To[a].push_back(b);
To[b].push_back(a);
}
For(root,1,n)
dp[root][0]=1,dp[root][1]=To[root].size()-1,dp[root][2]=(long long)(To[root].size()-1)*(To[root].size()-2)/2%mod;
long long ans=0;
For(root,1,n)
{
if (To[root].size()<4) continue;
sum0[root]=0;sum1[root]=0;sum2[root]=0;
sum01[root]=0;sum02[root]=0;sum11[root]=0;sum12[root]=0;
sum011[root]=0;sum012[root]=0;sum112[root]=0;
sum0112[root]=0;
For(i,0,(int)To[root].size()-1)
{
int v=To[root][i];
// sum0[root]=(sum0[root]+dp[v][0])%mod;
sum1[root]=(sum1[root]+dp[v][1])%mod;
sum2[root]=(sum2[root]+dp[v][2])%mod;
// sum01[root]=(sum01[root]+dp[v][0]*dp[v][1]%mod)%mod;
// sum02[root]=(sum02[root]+dp[v][0]*dp[v][2]%mod)%mod;
sum11[root]=(sum11[root]+dp[v][1]*dp[v][1]%mod)%mod;
sum12[root]=(sum12[root]+dp[v][1]*dp[v][2]%mod)%mod;
// sum011[root]=(sum011[root]+dp[v][0]*dp[v][1]%mod*dp[v][1]%mod)%mod;
// sum012[root]=(sum012[root]+dp[v][0]*dp[v][1]%mod*dp[v][2]%mod)%mod;
sum112[root]=(sum112[root]+dp[v][1]*dp[v][1]%mod*dp[v][2]%mod)%mod;
// sum0112[root]=(sum0112[root]+dp[v][0]*dp[v][1]%mod*dp[v][1]%mod*dp[v][2]%mod)%mod;
}
long long temp=1;
(temp*=sum1[root])%=mod;// 1
(temp*=sum1[root])%=mod;// 1 1
temp-=sum11[root];
temp=(temp%mod+mod)%mod;
(temp*=sum2[root])%=mod;// 1 1 2
temp-=sum1[root]*sum12[root]%mod;
temp+=sum112[root];
temp-=sum1[root]*sum12[root]%mod;
temp+=sum112[root];
temp=(temp%mod+mod)%mod;
// (temp*=sum0[root])%=mod;//1 1 2 0
// temp-=sum01[root]*sum1[root]%mod*sum2[root]%mod;
// temp+=sum011[root]*sum2[root]%mod+sum012[root]*sum1[root]%mod;
// temp-=sum0112[root];
// temp+=sum12[root]*sum01[root]%mod-sum0112[root];//1 2相同 ，1 0相同 ，两者分别不同 的那部分 不能多减
// temp-=sum01[root]*sum1[root]%mod*sum2[root]%mod;
// temp+=sum011[root]*sum2[root]%mod+sum012[root]*sum1[root]%mod;
// temp-=sum0112[root];
// temp+=sum12[root]*sum01[root]%mod-sum0112[root];//1 2相同 ，1 0相同 ，两者分别不同 的那部分 不能多减
// temp-=sum02[root]*sum1[root]%mod*sum1[root]%mod;
// temp+=sum012[root]*sum1[root]%mod+sum012[root]*sum1[root]%mod;
// temp-=sum0112[root];
// temp+=sum11[root]*sum02[root]%mod-sum0112[root];//1 1相同 ，2 0相同 ，两者分别不同 的那部分 不能多减
// temp=(temp%mod+mod)%mod;
(temp*=To[root].size()-3)%=mod;//加上头部，直接算即可，无需容斥
ans=(ans+temp)%mod;
}
printf("%lld\n",ans*power(2,mod-2)%mod);
}
return 0;
}1006 Sumire
题目难度：easy-medium
题目大意：计算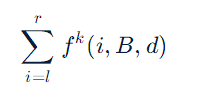
解题思路：一眼数位DP，枚举从哪一位开始后面的位可以任意放即可，比较麻烦的是要注意贴上界和贴下界（即当前位仍然属于前导0）
这题我明明是比较有把握做出来的，但是没有主动去做，可惜了。
说起来补题时有一个点要注意，把访问预处理数组写进power函数的时候一定要注意数组范围，否则就会一直RE。。。
另外还有注意每一个数位也用long long存比较好
还有state=1计算答案的时候还要注意别忘了乘sum。。。
赛时经历：
丁老师这题做了快2小时，最后因为把memset写进循环结果一直T。。。害，要吸取教训啊
参考代码：（state=0,1,2分别表示贴上界，任意取，贴下界（前导0））
查看代码
#include<iostream>
#include<cstdio>
#include<vector>
#define For(i,a,b) for(int i=a;i<=b;i++)
const long long mod=1e9+7;
std::vector<long long> Digit;
long long tot[100];
long long k,B,d;
long long c[100][100];
long long C(long long n,long long m)
{
if (m<0||m>n) return 0;
if (m==0||m==n) return 1;
return c[n][m];
}
long long powerB[100];
long long power(long long x,long long y)
{
if (y<0) return 0;
if (x==B-1&&y<=80) return powerB[y];//
long long ans=1;x%=mod;
while (y)
{
if (y&1) ans=ans*x%mod;
x=x*x%mod;y>>=1;
}
return ans;
}
void dfs(int pos,int state,long long sum,int cnt)
{
// printf("!! %d %d %lld %d\n",pos,state,sum,cnt);
if (!sum) return ;
if (pos<0)
{
tot[cnt]=(tot[cnt]+sum)%mod;
return ;
}
if (state==1)
{
For(i,cnt,60)
tot[i]=(tot[i]+sum*C(pos+1,i-cnt)%mod*power(B-1,(pos+1)-(i-cnt))%mod)%mod;
}
if (state==2)
{
dfs(pos-1,2,sum,cnt+(Digit[pos]==d));
if (Digit[pos]>d)
dfs(pos-1,1,sum*(Digit[pos]-1)%mod,cnt),dfs(pos-1,1,sum,cnt+1);
else
dfs(pos-1,1,sum*Digit[pos]%mod,cnt);
}
if (state==0)
{
dfs(pos-1,0,sum,cnt);
if (d) dfs(pos-1,1,sum*(B-2)%mod,cnt),dfs(pos-1,1,sum,cnt+1);
else dfs(pos-1,1,sum*(B-1)%mod,cnt);
}
}
long long Solve(long long r)
{
if (!r) return 0;
long long temp=r;Digit.clear();
while (temp)
{
Digit.push_back(temp%B);
temp/=B;
}
For(i,0,60) tot[i]=0;
dfs((int)Digit.size()-2,2,1,Digit[(int)Digit.size()-1]==d);
if (d!=0)
{
if (Digit[(int)Digit.size()-1]>d)
dfs((int)Digit.size()-2,1,Digit[(int)Digit.size()-1]-2,0),dfs((int)Digit.size()-2,1,1,1);
else
dfs((int)Digit.size()-2,1,Digit[(int)Digit.size()-1]-1,0);
}
else dfs((int)Digit.size()-2,1,Digit[(int)Digit.size()-1]-1,0);
dfs((int)Digit.size()-2,0,1,0);
// For(i,0,60) printf("?? %lld %d %lld\n",r,i,tot[i]);
long long ans=0;
For(i,1,60) ans=(ans+power(i,k)*tot[i]%mod)%mod;
return ans;
}
int main()
{
c[0][0]=1;
For(i,1,80)
{
c[i][0]=c[i][i]=1;
For(j,1,i-1) c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
}
int T;scanf("%d",&T);
while (T--)
{
long long l,r;
scanf("%lld%lld%lld%lld%lld",&k,&B,&d,&l,&r);
powerB[0]=1;For(i,1,80) powerB[i]=powerB[i-1]*(B-1)%mod;
printf("%lld\n",(Solve(r)-Solve(l-1)+mod)%mod);
}
return 0;
}1002 Independent Feedback Vertex Set
题目难度：easy
题目大意：通过一种特殊方式给定一张图，将这个图的点集分为两部分V1,V2，要求V1是一个独立集（任意两点无法到达），V2的诱导子图（一个边如果两端都属于V2，则这条边属于诱导子图）是一个森林。每个点有一个点权，询问V1的最大点权和是多少。
其中建图方式是先有一个三角形(1,2),(2,3),(1,2)。然后每次新加一个点i时从原图选择一条边(u,v)，新加入两条边(u,i),(v,i)。
解题分析：
答案必须包含每个三元环中的恰好一个点，因为一个点都不选则会破坏森林约束，选至少两个则会破坏独立集约束。
同时对于一对有至少两个公共点的三元环，确定了答案包含其中一个的某个点之后另一个也随之确定了。
因此答案只可能有三种，分别对应图中唯一的三染色方案（去重后）中的每一种颜色的点。
赛时经历：
没猜到结论。。。可惜了。而且时间也不够，害。
参考代码：
查看代码
#include<iostream>
#include<cstdio>
#define For(i,a,b) for(int i=a;i<=b;i++)
const int N=1e5+1000;
int vis[5][N];
long long a[N],ans[5];
int main()
{
int T;scanf("%d",&T);
while (T--)
{
int n;scanf("%d",&n);For(i,1,n) scanf("%lld",&a[i]);
vis[1][1]=1;vis[1][2]=0;vis[1][3]=0;ans[1]=a[1];
vis[2][1]=0;vis[2][2]=1;vis[2][3]=0;ans[2]=a[2];
vis[3][1]=0;vis[3][2]=0;vis[3][3]=1;ans[3]=a[3];
For(i,4,n)
{
int u,v;scanf("%d%d",&u,&v);
For(j,1,3)
{
if (vis[j][u]+vis[j][v]==0) ans[j]+=a[i],vis[j][i]=1;
else vis[j][i]=0;
// printf("!! %d %d %d %lld\n",i,j,vis[j][i],ans[j]);
}
}
printf("%lld\n",std::max(std::max(ans[1],ans[2]),ans[3]));
}
return 0;
}1007 Weighted Beautiful Tree
题目难度：medium
题目大意：给定一个树，每个点有点权wn，代价c，每条边有边权we。
将某个点的点权从wn变为wn'需要花费c*|wn-wn'|的代价，问如何花费最小代价使得对于每一条边(u,v)满足 min(wnu,wnv)<=we<=max(wnu,wnv)。
解题分析：
树形DP，dp[root][0,1]表示root的权值<=父边和root的权值大于等于父边时，root子树的代价。
然后将每个点的所有子节点按照边权排序，枚举root的权值的取值范围即可。另外需要一批一批处理权值相同的点，还得注意，如果wnu=we，那么wnv实际上是可以任意取值的。
赛时经历：
压根没开。。。
参考代码：
查看代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<vector>
#define For(i,a,b) for(int i=a;i<=b;i++)
const long long INF=0x3f3f3f3f3f3f3f3f;
const int N=1e5+1000;
long long dp[N][2],c[N],w[N];
std::vector<std::pair<long long,int> > To[N];
void Solve(int now,int opt,long long L,long long R,long long sum)
{
if (L<=R)
{
if (w[now]<L) dp[now][opt]=std::min(dp[now][opt],sum+c[now]*(L-w[now]));
else if (w[now]<=R) dp[now][opt]=std::min(dp[now][opt],sum);
else dp[now][opt]=std::min(dp[now][opt],sum+c[now]*(w[now]-R));
}
}
void dfs(int now,int pa,long long pw)
{
For(i,0,(int)To[now].size()-1) if (To[now][i].second==pa)
{
For(j,i,(int)To[now].size()-2) To[now][j]=To[now][j+1];
To[now].pop_back();
break;
}
if (To[now].empty())
{
if (w[now]<=pw) dp[now][0]=0;else dp[now][0]=c[now]*(w[now]-pw);
if (w[now]>=pw) dp[now][1]=0;else dp[now][1]=c[now]*(pw-w[now]);
return ;
}
long long sum=0;
For(i,0,(int)To[now].size()-1)
{
int v=To[now][i].second;
dfs(v,now,To[now][i].first);
sum+=dp[v][1];
}
dp[now][0]=dp[now][1]=INF;
long long pL,pR;if (pa) pL=pR=pw;else pL=-INF,pR=INF;
long long nowL,nowR,L,R;
For(i,0,(int)To[now].size()-1) if (To[now][i].second!=pa)
{
if (i==0) nowL=-INF,nowR=To[now][0].first-1;
else nowL=To[now][i-1].first+1,nowR=To[now][i].first-1;
L=std::max(nowL,pL);R=nowR;Solve(now,1,L,R,sum);
L=nowL;R=std::min(nowR,pR);Solve(now,0,L,R,sum);
int j=i;while (j+1<To[now].size()&&To[now][j+1].first==To[now][i].first) j++;
long long temp=sum;
For(k,i,j)
{
int v=To[now][k].second;
temp=temp-dp[v][1]+std::min(dp[v][0],dp[v][1]);
}
nowL=nowR=To[now][i].first;
L=std::max(nowL,pL);R=nowR;Solve(now,1,L,R,temp);
L=nowL;R=std::min(nowR,pR);Solve(now,0,L,R,temp);
For(k,i,j)
{
int v=To[now][k].second;
sum=sum-dp[v][1]+dp[v][0];
}i=j;
}
nowL=To[now][(int)To[now].size()-1].first+1;nowR=INF;
L=std::max(nowL,pL);R=nowR;Solve(now,1,L,R,sum);
L=nowL;R=std::min(nowR,pR);Solve(now,0,L,R,sum);
}
int main()
{
int T;scanf("%d",&T);
while (T--)
{
int n;scanf("%d",&n);
For(i,1,n) scanf("%lld",&c[i]);
For(i,1,n) scanf("%lld",&w[i]);
For(i,1,n) To[i].clear();
For(i,1,n-1)
{
long long u,v,w;scanf("%lld%lld%lld",&u,&v,&w);
To[u].push_back(std::make_pair(w,v));
To[v].push_back(std::make_pair(w,u));
}For(i,1,n) std::sort(To[i].begin(),To[i].end());
if (n==1) {printf("%d\n",0);continue;}
dfs(1,0,0);printf("%lld\n",std::min(dp[1][0],dp[1][1]));
}
return 0;
}
浙公网安备 33010602011771号