道长的算法笔记：网络流概念引入

本篇内容是对蒋炎岩老师讲义整理，强烈建议观看原视频！

(一)网络流引入

　最短路、网络流等是最小费用流的一个特列，最小费用流其实是线性规划的一个特例。很多现实中的问题均可规约变为线性规划问题，通常竞技算法会解决整数线性规划问题。线性规划之上，又有凸优化等更加复杂的问题，这一切都离不开 对偶理论。例如，最大流与最小割便是一组对偶问题。

　给定一个有向图，寻找一条 \(s \rightarrow t\) 路径，我们通常会用 BFS 或 DFS 方法，

• 如果能找到，路径就存在
• 如果找不到，路径不存在

　然而这是算法的做法，并非数学意义上面的证明，如何给出证明呢？

　一个粗暴的证明是枚举所有节点之间的路径，检查路径上面的连边是否都存在于边集，若是则路径合法，否则路径不合法，如果所有 \(s \rightarrow t\) 路径均不合法，那么 \(s \rightarrow t\) 路径不存在，虽然这种证明严格，但若图节点数量较多则其证明「篇幅太长」，你可以列满一张纸都证不完，为此我们需要考更加简洁的证明方法。

　由于 DFS 与 BFS 会拓展其邻居节点，所以不妨把已经达到的顶点记作集合 \(S\)，未到达的顶点都记作 \(T\)，那么对于任意 \(v \in S, u \in T\) ，都不存在到达 \((v,u)\) ，但有可能存在 \((u,v)\)。

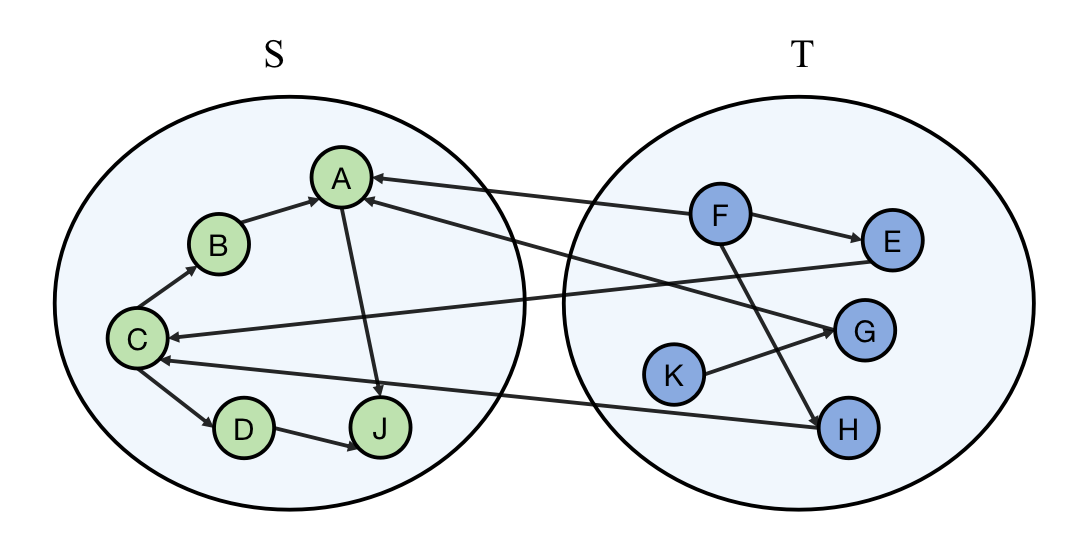
　上面的表述其实就是一个大小等于零的 \(cut\)，定义这样的两个集合 \(S、T\)，其中 \(cut\) 大小等于 \(S\) 能够到达 \(T\) 所有连边数。因而，只要找到一个大小为零 \(cut(s,t)\) 即可否认所有 \(s \rightarrow t\) 路径排列。

如果要求图中存在多少不相交的路径？又该如何呢？

• \(k = 1\)，验证连通性问题

• \(k =2\)，似乎很难直接验证

  • 尝试验证问题的反面：如何证明不存在两条 \(s \to t\) 路径
    • 如果发现一个 \(cut(s,t)=0\)，说明二者至多零条路径
    • 如果发现一个 \(cut(s,t)=1\)，说明二者至多一条路径
    • 如果发现一个 \(cut(s,t)=2\)，说明二者至多两条路径
  • 如果找到了 \(cut(s,t)=l\)，那么 \(k \leq l\)，作为上界
  • 如果找到了不相交路径数量 \(m\)，那么 \(m \leq k\)， 作为下界

　如果 \(m = l\)，说明图中存在 \(k=m=l\) 数量的不相交路径。

　一个直观但是不正确的算法是采用贪心策略寻找路径，每次寻找一条边路径，找到便将路径去掉，不停重复，直至找不到路径为止，然而这样的算法很容易找出反例。

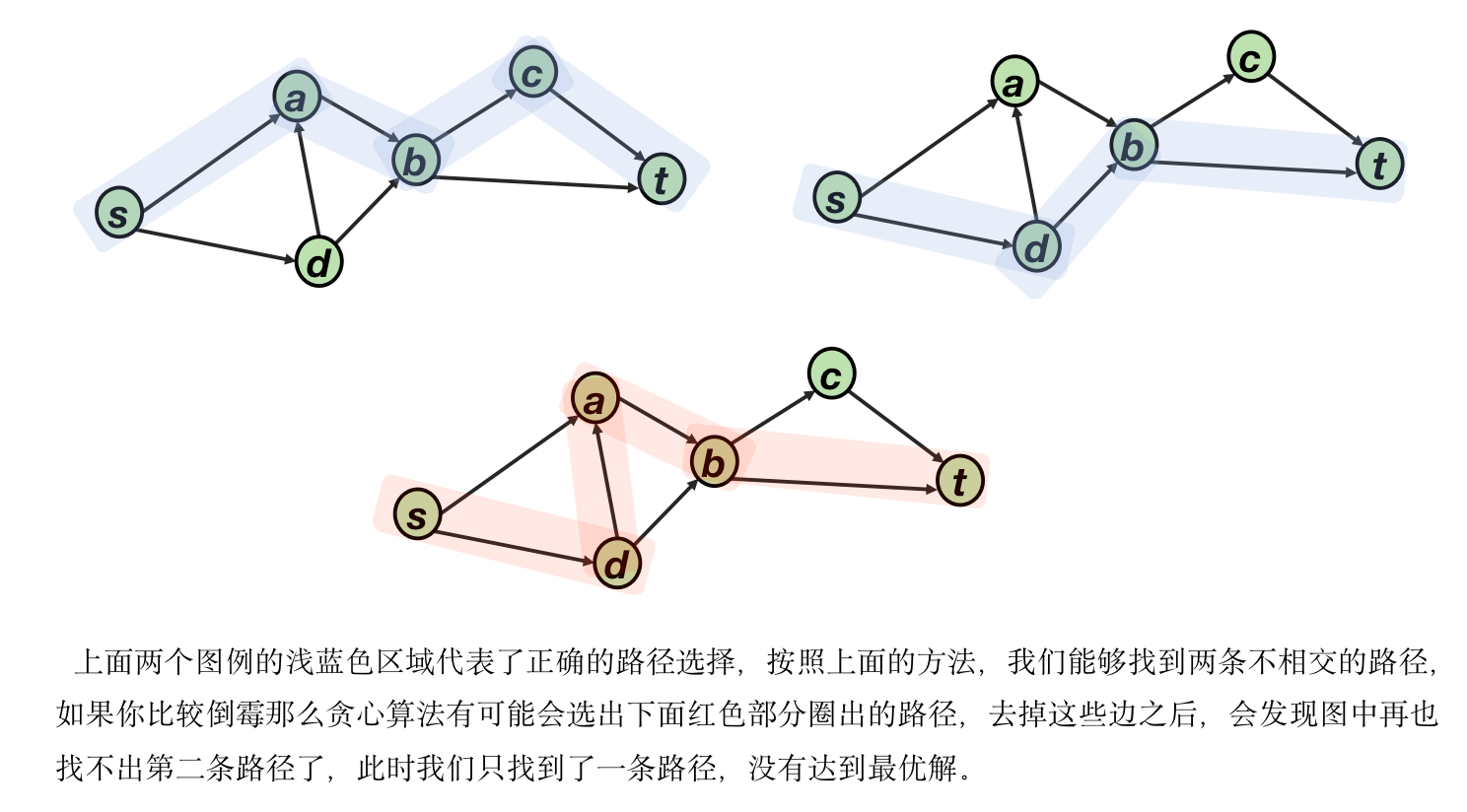
　如果能够引入某种机制，使得我们已经犯错的情况之下仍然能够找到下一条路径，那么问题也就解决了。也就是说，我们希望找到一条新路径的同时，纠正旧错误。这个机制其实就是Ford-Fulkerson 算法提出的「残留网络」，当残留网络已经无法找到路径，此时 \(cut(s,t)=0\)，算法终止，残留网络与原始网络的区别在于，已经找出的路径是取反的，其余部分都是一样的。

　残留网络与原始网络分表记作 \(G_{r}、G_{o}\)，那么 \(cut(G_r|s,t)=0\) 对应 \(cut(G_o|s,t)=m\)，其中 \(m\) 代表我们找到的路径数量。也就是说，如果我们能在原始网络找出路径\(P_1,P_2,P_3,...,P_m\)，若就这些路径取反，那么残留网络将不再能找到\(s\to t\) 路径。

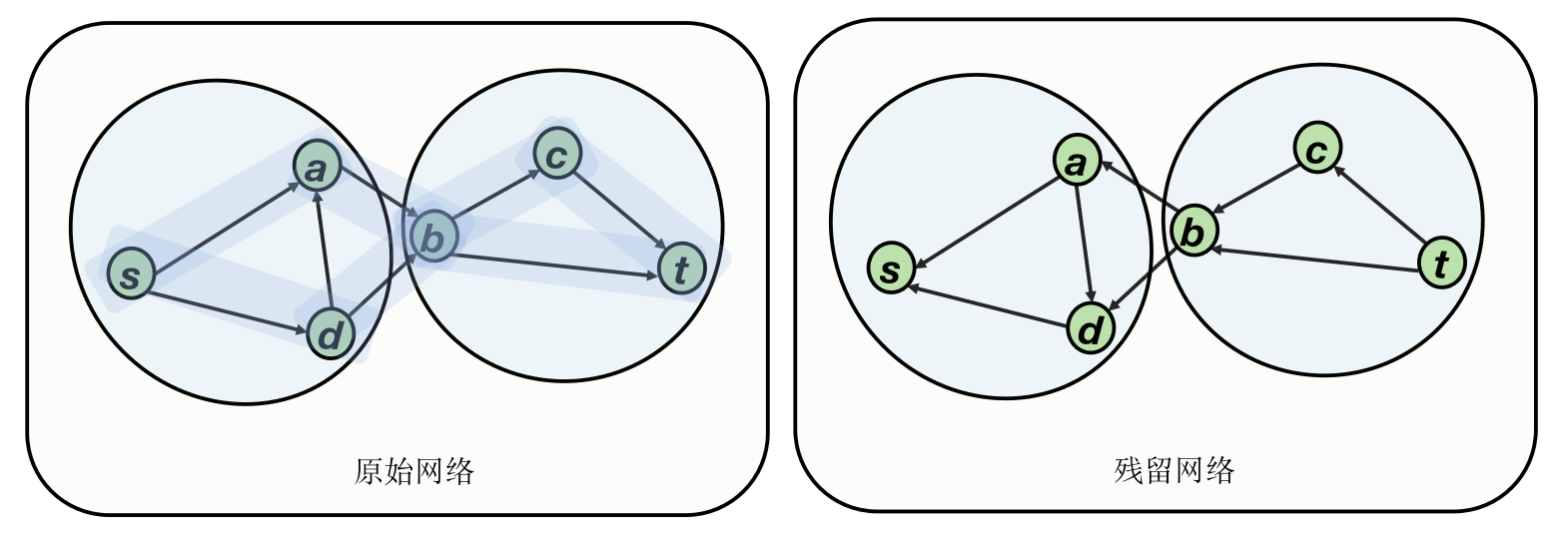
　不妨记我们找到的路径\(P_1,P_2,P_3...P_m\)，残留网络上面的路径相当于原图路径取反，如果我们能够证明这些路径恰好只从 \(T\) 穿过 \(S\) 一次，说明 \(cut(G_o|s,t)=m\) ，这条性质使用反证法很容易证明，如果穿过多次，那么 \(cut(G_r|s,t)\neq 0\)，与算法的终止条目矛盾。

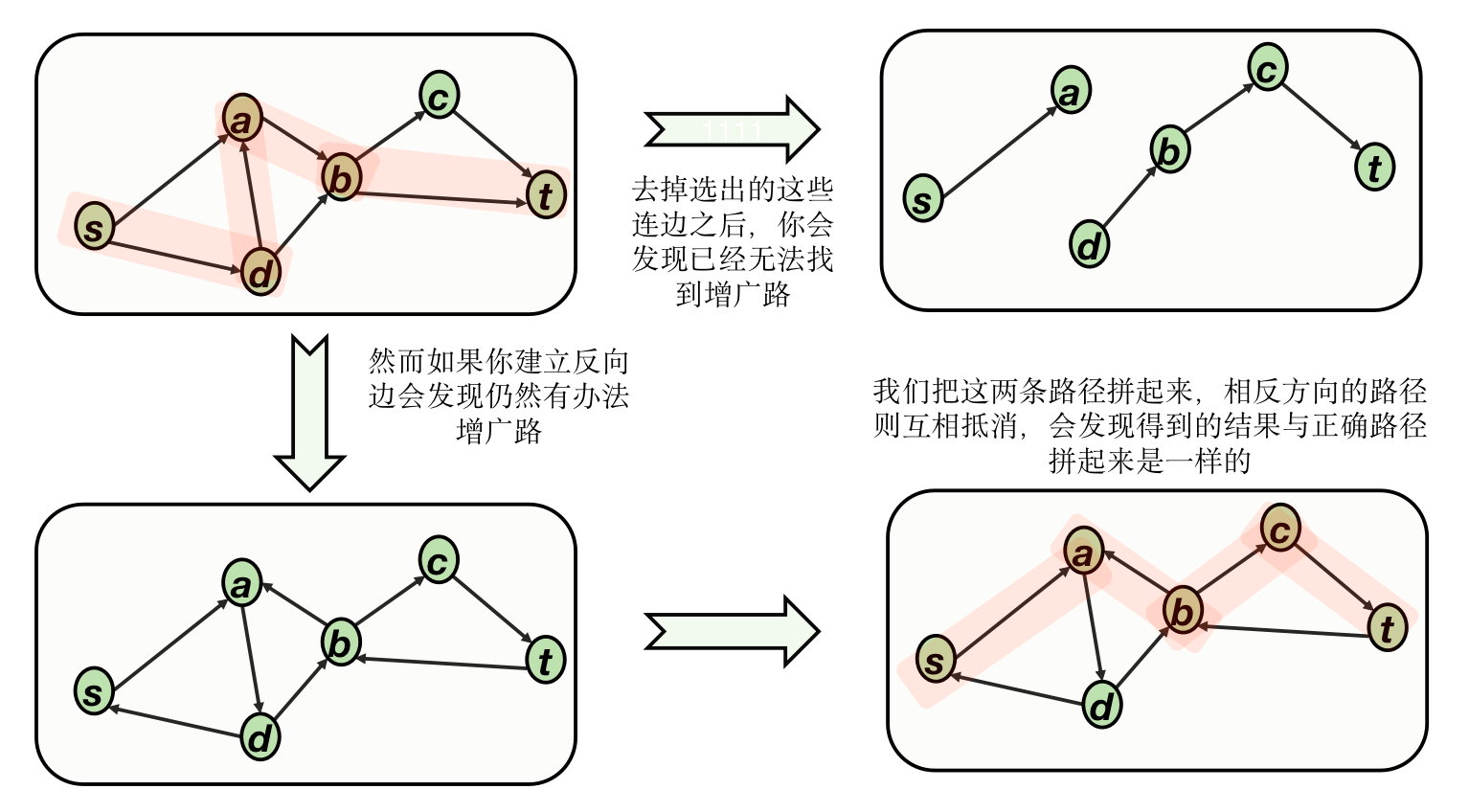
　由于原始网络找到了一个 cut 等于 \(m\)，且找到的路径数量等于 \(m\)， 因而网络存在不相交的路径数量等于 \(m\)，这个其实就是大名鼎鼎的 Ford-Fulkerson 算法！对于带权图，我们只要把权值 \(w\) 看成 \((u,v)\) 之间的连边数量即可，我们通常会把权值称为「容量」，寻找不相交路径数量的问题也就变成了「最大流」问题，其对偶问题即为「最小割」问题。最大流于最小割是图像处理 「Grabcut」 算法的核心。

(二)最大流最小割定理

　最小割是指把网络分为两个不相交的集合 \(S\) 与 \(T\)，使得 \((s,t)\) 容量最小，其中 \(s \in S\)， \(t \in T\)，网络的最大流等于最小割，形式化表达写作 \(f(s,t)_{max} = c(s,t)_{min}\)，我们假设最小割小于最大流，那么说明割断这些连边之后，网络流如果仍然没有达到最大，也就是说仍然能够找到 \(s \to t\) 增广路，与割定义矛盾，因而最小割应当大于等于最大流。接着我们给出一个最小割等于最大流的构造方案即可。我们算出最大流之后，再对残留网络DFS，能够到达的顶点构成集合 \(S\)，无法到达顶点全部记作 \(T\)，此时的分割方案就是最小割。

　如果对于带权图，要求最小割大小与最小割的边数(其实就是割断的边数)，我们通常需要跑一遍最大流，得到最小割大小，然后重新建图，把边权设为 1，再跑一遍最大流，得到最小割需要割断的边数。

支持作者