道长的算法笔记：简单博弈论

(一) Nim博弈

　所谓 Nim 博弈是指，给定一堆石子，第 \(i\) 堆物品共有\(A_i\)，两个玩家轮流行动，每次可以任选一堆，从中取走任意数量的物品，可把一堆取光，但不可不取，两人都采取最优策略，问先手是否必胜，也即第一个行动的称为先手。Nim 博弈不存在的平局，只有先手必胜与先手必败两种情况，

　那么当且仅当，

\[x=\bigoplus_{i=0}^n A_i \neq 0 \]

　Nim 博弈先手必胜，假设 \(x\) 二进制最高位第一个\(1\)落在第\(k\)位，此时必有一堆石子\(A_i\)第k 位也是\(1\)，而且会有 \(A_i\oplus x < A_i\)，所以此时只要取走 $A_i - A_i\oplus x $ 个数的石子，使得 \(A_i\) 变为\(A_i - x\)，那么原来的石子异或和会变成 \(x\oplus A_i \oplus (A_i\oplus x)=0\)，也即存在一个取石子方案使得敌手陷入必败的状态。

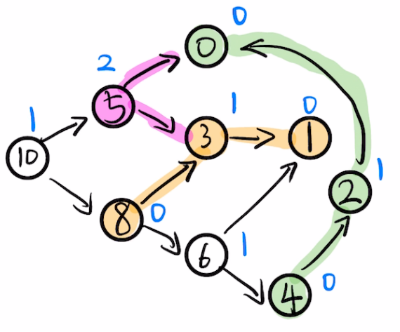
　结合 \(SG\) 函数，关于SG 函数定义 参考此处，Nim 博弈能被推广到更为一般的情况，首先我们来定义有向图游戏，给定一个有向无环图，图中有唯一的一个起点，在起点放置一个棋子，两名玩家交替的沿着有向边移动这个棋子，直至无法移动，轮到某一方且这一方无妨移动棋子的时候，则其输掉了游戏。Nim 博弈等多种博弈均可转为有向图游戏，但是一个复杂的博弈问题，往往是由多个有向图游戏构成的，均以起点\(s_i\)表示每个有向图\(G_i\)，
　
那么当且仅当，

\[x=\bigoplus_{i=0}^n SG(s_i) \neq 0 \]

本次博弈先手必胜，因为如果 \(SG(s_i)=k\)，那么这个 \(SG(s_i)\) 能被转移落到 \(0 \leq SG(·)<k\)，相当于是说每个 \(SG\)描述了一堆石子，石子个数 \(k-1\)，可以每次可以拿走任意多数量但不可以不拿。如图所示，\(SG(5)=2\)，则其可以转为 \(\{0,1\}\) 局面。