道长的算法笔记：最近公共祖先

(一)最近公共祖先

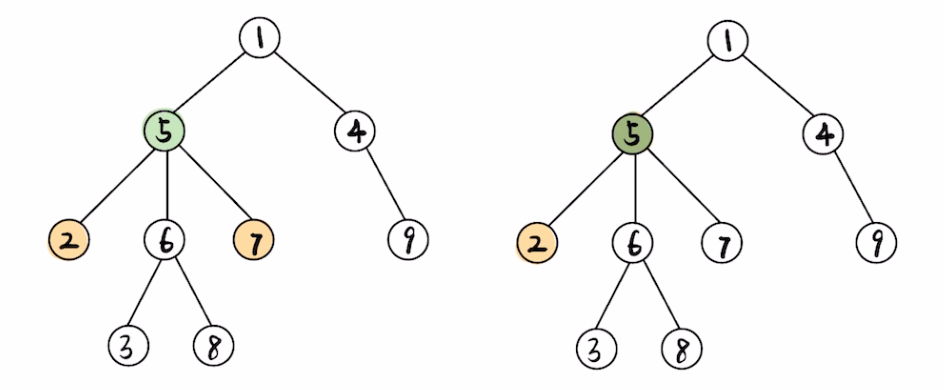
　如图所示，树节点 \(2\) 与 \(7\) 公共祖先即为图中的树节点 \(5\)，又如图中树节点 \(2\) 与 \(5\) 公共祖先即为 \(5\)；以下内容参考了 OI-Wiki，首先大致了解一下公共祖先具有下列性质:

• 如果 \(u\) 不为 \(v\) 公共祖先且 \(v\) 不为 \(u\)，那么 \(u\) 与 \(v\) 位于两颗不同的子树
• 前序遍历中 \(LCA(S)\) 出现在顶点集合 \(S\) 之前
• 后序遍历中 \(LCA(S)\) 出现在顶点集合 \(S\) 之后
• 两个树节点的最近公共祖先必定在树上两顶点之间的最短路径上(非常重要的性质)
• 根据并集性质可知， \(LCA(S\cup T)\) = \(LCA(LCA(S),LCA(T))\)
• 根据容斥原理可知，\(d(u,v)= h(u)+h(v)-2h(LCA(u,v))\)

　朴素的做法是递归遍历整棵树，从各个子树搜索两个顶点，如果仅有一棵子树不为空，其它子树均为空，此时这颗子树的根节点即为公共祖先。若有两颗子树不为空，此时根节点即为公共祖先，然而如果频繁的问询树上两个节点之间的公共祖先，每一次都要遍历整棵树，朴素方法的复杂度显然是会超时的，因而求解LCA问题的常用三种做法分别是使用倍增法、Tarjan+并查集(离线)、树链剖分方法，另外一种不那么常用的方法是转为欧拉序采用RMQ查询，四种方法都非常重要，不仅是在 LCA 问题，更是其它算法的基础，必须掌握。下面本节的四个子章节均以 洛谷P3379 为例，读完之后可尝试前往 HDU2586 使用三种常用方法进行练习，倍增、树链剖分、Tarjan 三种解法的参考代码详见于 [1] [2] [3]之中。

(1.1)倍增算法

　倍增算法通过一遍 dfs 预处理数组 \(ft_{x,i}\)，使得游标能够快速移动，大幅减少了游标跳转次数，其中\(ft_{x,i}\) 代表顶点 \(x\) 第\(2^i\)个祖先，这种思想也在稀疏表(Sparse Table)专题中出现。由于 \(2^i=2^{i-1} + 2^{i-1}=2 \times 2^{i-1}\) 这个性质可知, \(ft_{x,i}\) 能够通过倍增思想递推方程获得，详见下列代码。

vector<int> edges[MAXN];
int dep[MAXN], ft[MAXN][25];

// 倍增法打表查询公共祖先
void dfs(int u, int father){
    dep[u] = dep[father] + 1;
    ft[u][0] = father; // 向上跳跃一个顶点显然就是其父节点
    for(int i = 1; i <= 20; i++){
        ft[u][i] = ft[fa[u][i - 1]][i - 1]; // 蕴含倍增思想的递推方程
    } 
    for(int v :  edges[u]){
        if(v != father){
            dfs(v, u);
        }
    }
}

int lca(int u, int v){
    if(dep[u] < dep[v]) 
        swap(u, v);
    // 顶点 u 处在更深的位置
    for(int i = 20; i>=0; i--){
        if(dep[ft[u][i]] >= dep[v]){
            u = ft[u][i];
        }
    }
    if(u == v) return v;
    for(int i = 20; i >= 0; i--){
        if(ft[u][i] != ft[v][i]){
            u = ft[u][i], v = ft[v][i];
        }
    }
    return ft[u][0];
}

(1.2)树链剖分

　树链剖分算法是把一棵树分为重链、轻链，其中 \(LCA\) 即为两个游标跳转到同一条重链上时深度较小的那个游标所指向的树节点。重链是由第一个指向重节点的轻节点以及其随后所有重节点组成的，所谓重节点也即子树规模最大的节点。
　树链剖分需要两次 dfs，第一次深搜获取各个节点深度，父节点，重链头结点，以及子树大小等信息，获取这些基本信息之后，再对整个树进行剖分，第二次的深搜重，优先朝着重节点往下走，并以链头标记一个一个重链，直至没有重子节点，也即无子节点。

vector<int> edges[MAXN];
int dep[MAXN], ft[MAXN], siz[MAXN], hev[MAXN], top[MAXN];
int n, m, s, a, b;


// 深搜获取深度，父节点，重链头节点，以及子树大小
void tree_build(int u, int fahter){
    ft[u] = fahter, dep[u] = dep[fahter] + 1, siz[u] = 1;
    for(int v : edges[u]){
        if(v == fahter)
            continue;
        tree_build(v, u);
        siz[u] += siz[v];
        if(siz[hev[u]] < siz[v]) hev[u] = v;
    }
}

// 获取了树结构基本信息之后开始树链剖分，通过链头唯一的标识一条重链
void tree_decomposition(int u, int t){
    top[u] = t;
    if(!hev[u]) return;
    tree_decomposition(hev[u], t);
    for(int v: edges[u]){
        if(v == ft[u] || v == hev[u])
            continue;
        tree_decomposition(v, v);
    }
}

　这种使用链头标记整个重链的思想，挺像并查集使用一个元素代表一块连通分量的，搜索结束之后，我们移动较深的重链头更深的节点，把它移到其链头父节点的位置，如果仍然不在同一条重链，我们继续移动较深的树节点，直至两个节点位于同一条重链。此时\(u, v\) 当中较浅的，也即位于较上层次的，即为二者的公共祖先。

int lca(int u, int v){
    while(top[u] != top[u]){
        if(dep[top[u]] < dep[top[v]])
            swap(u, v);
        u = ft[top[u]];
    }
    return dep[u] < dep[v] ? u : v;
}

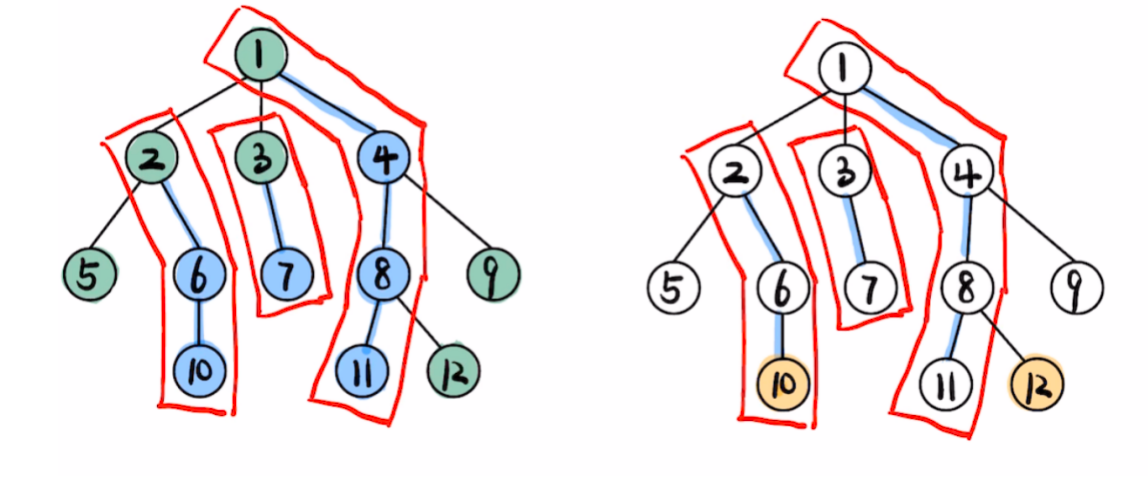
　例如，我们询问 \(LCA(10,12)\)，已知 \(top[10] = 2\), \(top[12] = 12\)，两者链头不相等，看谁的链头更深一点，显然，dep[12] > dep[2]，所以较深的树节点，要往上爬至其链头父节点的位置， \(u = ft[top[12]] = 8\)，二者仍然不在同一条重链上面，此时 \(top[10]=2\)，\(top[8]=1\)，显然树节点 \(10\) 所在链的链头 \(2\) 更深一点，移到其父节点位置，此时，\(u = 1\)，二者已经处在同一条链式，显然，树节点 \(1\) 相较于树节点 \(8\) 更浅，返回 \(1\) 作为 \(LCA(10,12)\) 问询的答案。

(1.3)塔扬算法

　塔扬(Tarjan)，一位计算机科学家，以其命名的算法非常多，且都非常重要，个别教将其译为塔扬。Tarjan 算法是一个离线算法，这个算法巧妙的利用了并查集求解公共祖先，首先递归向下，走到最底部的时候向上返回的时候，方才更新每个树节点父节点，然后查询当前节点 \(u\) 包含的问询 \((u,v)\)，如果 \(v\) 已经访问，说明其信息已在搜索完毕向上返回的过程中获取，故用并查集的 \(find(v)\) 函数寻找其公共祖先。

vector<int> edges[MAXN];
vector<ii> query[MAXN];
int ft[MAXN], vist[MAXN], ans[MAXN];
int n, m, s, a, b;

int find(int x){
    return x != ft[x] ? (ft[x] = find(ft[x])) : ft[x];
}

// 递归函数调用处能被视为一条分界线，
// 其上是递归之前要做的内容，其下是递归返回之后要做的内容，
void tarjan(int u){
    vist[u] = true;
    for(int v : edges[u]){
        if(!vist[v]){
            tarjan(v);
            ft[v] = u; // 返回的时候记录父节点
        }
    }// u 所有子节点均被搜索，此时向上返回到达 u，此时每个已被访问的树节点均已携带父节点信息
    for(auto q : query[u]){
        int v = q.first, i = q.second;
        if(vist[v]){
            ans[i] = find(v); // 如果问询(u,v)之中，v 已被访问则通过find 获取其公共祖先信息
        }
    }
}

(二)树结构欧拉序RMQ查询

Waiting...